(三)动手学线性神经网络:从数学原理到代码实现
1 线性回归
线性回归是一种基本的预测模型,用于根据输入特征预测连续的输出值。它是机器学习和深度学习中最简单的模型之一,但却是理解更复杂模型的基础。
1.1 线性回归的基本元素
概念理解:
线性回归假设输入特征和输出之间存在线性关系。具体来说,假设有一个输入特征向量 x x x 和一个目标值 y y y,线性回归模型的目标是找到一个线性函数 f ( x ) f(x) f(x) ,使得 f ( x ) f(x) f(x)尽可能接近 y y y。
线性回归模型的基本形式为:
y ^ = X w + b \hat{y} = Xw + b y^=Xw+b
其中:
- X X X是输入特征矩阵,每一行表示一个样本,每一列表示一个特征。
- w w w 是权重向量,表示每个特征的权重。
- b b b是偏置项,是一个标量,用于调整模型的整体偏移。
- y ^ \hat{y} y^ 是预测值,是一个向量,表示每个样本的预测结果。
代码示例:
假设我们有一个简单的线性回归问题,输入特征是一个一维向量 X X X,目标值是一个标量 y y y。
import numpy as np
import matplotlib.pyplot as plt# 生成数据
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)# 绘制数据
plt.scatter(X, y)
plt.xlabel('X')
plt.ylabel('y')
plt.title('Generated Data')
plt.show()
1.2 向量化加速
概念理解:
向量化是一种利用矩阵和数组操作来替换显式循环的技术。它可以显著提高代码的执行效率,尤其是在现代硬件(如GPU)上。在深度学习中,向量化操作是构建高效模型的关键。
代码示例:
在上述数据生成代码中,我们使用了 NumPy 的向量化操作来生成数据。这种操作比使用循环生成数据要快得多。
1.3 正态分布与平方损失
概念理解:
线性回归通常假设误差项(即真实值与预测值之间的差异)服从正态分布。因此,线性回归常用的损失函数是均方误差(MSE),它衡量了预测值与真实值之间的平方误差。
均方误差的公式为:
[ \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 ]
其中:
- ( y_i ) 是第 ( i ) 个样本的真实值。
- ( \hat{y}_i ) 是第 ( i ) 个样本的预测值。
- ( n ) 是样本总数。
代码示例:
定义均方误差损失函数。
def mean_squared_error(y_true, y_pred):return ((y_true - y_pred) ** 2).mean()# 测试损失函数
y_true = np.array([3, 2, 4, 5])
y_pred = np.array([2.5, 2, 4, 5.5])
mse = mean_squared_error(y_true, y_pred)
print(f'Mean Squared Error: {mse}')
1.4 从线性回归到深度网络
概念理解:
线性回归是深度学习的一个特例,其中网络仅包含一个线性层。深度学习模型通过堆叠多个线性层和非线性激活函数来处理更复杂的数据。这些非线性激活函数(如 ReLU、Sigmoid)使得模型能够学习数据中的非线性关系。
代码示例:
构建一个简单的深度神经网络模型(包含一个隐藏层)。
import torch
import torch.nn as nn# 定义模型
class SimpleNN(nn.Module):def __init__(self):super(SimpleNN, self).__init__()self.linear1 = nn.Linear(1, 10) # 输入特征维度为1,隐藏层维度为10self.relu = nn.ReLU()self.linear2 = nn.Linear(10, 1) # 输出维度为1def forward(self, x):x = self.linear1(x)x = self.relu(x)x = self.linear2(x)return x# 实例化模型
model = SimpleNN()# 打印模型结构
print(model)
1.5 训练线性回归模型
概念理解:
训练线性回归模型的目标是找到最优的权重 w w w和偏置 b b b,使得损失函数(如均方误差)最小。这通常通过优化算法(如梯度下降法)来实现。
代码示例:
训练一个简单的线性回归模型。
import torch.optim as optim# 转换数据为张量
X_tensor = torch.from_numpy(X).float()
y_tensor = torch.from_numpy(y).float()# 定义模型
model = nn.Linear(1, 1)# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)# 训练模型
num_epochs = 1000
for epoch in range(num_epochs):# 前向传播y_pred = model(X_tensor)loss = criterion(y_pred, y_tensor)# 反向传播optimizer.zero_grad()loss.backward()optimizer.step()if (epoch + 1) % 100 == 0:print(f'Epoch {epoch + 1}, Loss: {loss.item():.4f}')# 打印训练后的参数
print(f'Estimated weight: {model.weight.item():.2f}, Estimated bias: {model.bias.item():.2f}')
1.6 模型评估
概念理解:
评估线性回归模型的性能通常使用均方误差(MSE)或其他回归指标(如均方根误差 RMSE、平均绝对误差 MAE)。
代码示例:
评估训练后的模型性能。
# 使用训练后的模型进行预测
y_pred = model(X_tensor).detach().numpy()# 计算均方误差
mse = mean_squared_error(y, y_pred)
print(f'Mean Squared Error: {mse:.4f}')# 绘制真实值和预测值
plt.scatter(X, y, color='blue', label='True data')
plt.plot(X, y_pred, color='red', linewidth=2, label='Fitted line')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression')
plt.legend()
plt.show()
通过上述步骤,你可以从理论和实践两个方面理解线性回归模型。线性回归是深度学习的基础,掌握它有助于你更好地理解和构建更复杂的神经网络模型。
2 线性回归的从零开始实现
2.1 生成数据集
首先生成一个简单的模拟数据集用于训练和测试我们的线性回归模型。我们假设真实模型是 y = 4 + 3 X y= 4 + 3X y=4+3X + 噪声 ,其中噪声服从正态分布。
import numpy as np# 设置随机种子以确保结果可复现
np.random.seed(42)# 生成训练数据
X_train = 2 * np.random.rand(100, 1) # 特征
y_train = 4 + 3 * X_train + np.random.randn(100, 1) # 目标值,包含噪声# 生成测试数据
X_test = 2 * np.random.rand(20, 1)
y_test = 4 + 3 * X_test + np.random.randn(20, 1)
2.2 数据预处理
在训练模型之前,通常需要对数据进行预处理。在这里,我们将数据转换为适合进行矩阵运算的形式。
# 数据预处理:将数据转换为矩阵形式
X_train = np.hstack((np.ones((X_train.shape[0], 1)), X_train)) # 添加偏置项
X_test = np.hstack((np.ones((X_test.shape[0], 1)), X_test))
2.3 初始化模型参数
初始化线性回归模型的权重向量。在我们这个简单例子中,权重向量包含偏置项和特征的系数。
# 初始化权重向量(包括偏置项)
theta = np.random.randn(2, 1) # 2行1列,对应偏置和一个特征的权重
2.4 定义模型
定义线性回归模型的正向传播过程。这一步就是根据当前的权重向量计算预测值。
# 定义线性回归模型
def linear_regression(X, theta):return X.dot(theta)
2.5 定义损失函数
选择均方误差(MSE)作为损失函数,它衡量了预测值与真实值之间的差异。
# 定义均方误差损失函数
def mean_squared_error(y_true, y_pred):return np.mean((y_true - y_pred) ** 2)
2.6 定义优化算法
使用小批量随机梯度下降法(Mini-batch Gradient Descent)来优化模型参数。我们手动计算梯度并更新参数。
# 定义小批量随机梯度下降法
def minibatch_gradient_descent(X, y, theta, learning_rate, epochs, batch_size):m = len(y)for epoch in range(epochs):# 打乱数据indices = np.arange(m)np.random.shuffle(indices)X_shuffled = X[indices]y_shuffled = y[indices]# 分成小批次for i in range(0, m, batch_size):X_batch = X_shuffled[i:i+batch_size]y_batch = y_shuffled[i:i+batch_size]# 正向传播y_pred = linear_regression(X_batch, theta)# 计算梯度gradient = (2 / batch_size) * X_batch.T.dot(y_pred - y_batch)# 更新参数theta -= learning_rate * gradient# 每隔一定迭代次数打印损失if epoch % 100 == 0:y_pred = linear_regression(X, theta)loss = mean_squared_error(y, y_pred)print(f'Epoch {epoch}, Loss: {loss}')return theta
2.7 训练模型
现在开始训练模型,使用我们刚才定义的梯度下降法来优化模型参数。
# 设置超参数
learning_rate = 0.01
epochs = 1000
batch_size = 10# 训练模型
theta = minibatch_gradient_descent(X_train, y_train, theta, learning_rate, epochs, batch_size)# 输出最终的模型参数
print(f'Estimated parameters: {theta.flatten()}')
2.8 模型评估
训练完成后,我们对模型进行评估,看看它在测试集上的表现。
# 在测试集上进行预测
y_test_pred = linear_regression(X_test, theta)# 计算测试集上的损失
test_loss = mean_squared_error(y_test, y_test_pred)
print(f'Test Loss: {test_loss}')# 可视化结果
import matplotlib.pyplot as plt# 绘制训练数据和测试数据
plt.scatter(X_train[:, 1], y_train, label='Training Data')
plt.scatter(X_test[:, 1], y_test, label='Test Data')# 绘制预测线
X_plot = np.linspace(0, 2, 100).reshape(-1, 1)
X_plot = np.hstack((np.ones((X_plot.shape[0], 1)), X_plot))
y_plot_pred = linear_regression(X_plot, theta)
plt.plot(X_plot[:, 1], y_plot_pred, color='red', label='Fitted Line')plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression from Scratch')
plt.legend()
plt.show()
3 线性回归的简洁实现
将使用PyTorch的高级API来实现线性回归模型。这种方法更加简洁,利用了PyTorch的内置功能,减少了代码量并提高了开发效率。
3.1 生成数据集
我们继续使用之前生成的数据,但如果需要重新生成,可以使用以下代码:
import numpy as np
import torch
from torch.utils.data import TensorDataset, DataLoader# 生成数据集
np.random.seed(42)
X = 2 * np.random.rand(100, 1) # 100个样本,每个样本1个特征
y = 4 + 3 * X + np.random.randn(100, 1) # 真实模型 y = 3x + 4 加上一些噪声# 转换为张量
X_tensor = torch.from_numpy(X).float()
y_tensor = torch.from_numpy(y).float()# 创建数据集和数据加载器
dataset = TensorDataset(X_tensor, y_tensor)
data_loader = DataLoader(dataset, batch_size=10, shuffle=True)
3.2 定义模型
使用PyTorch的 nn.Linear 来定义线性回归模型:
import torch.nn as nn# 定义模型
model = nn.Linear(1, 1) # 输入特征维度为1,输出维度为1
3.3 初始化模型参数
初始化模型的权重和偏置:
# 初始化参数
nn.init.normal_(model.weight, mean=0, std=0.01)
nn.init.zeros_(model.bias)
3.4 定义损失函数
使用PyTorch内置的均方误差损失函数:
# 定义损失函数
loss_fn = nn.MSELoss()
3.5 定义优化算法
使用PyTorch的 torch.optim 模块来定义优化器:
# 定义优化算法
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
3.6 训练模型
训练模型并评估性能:
# 训练模型
num_epochs = 100
for epoch in range(num_epochs):for X_batch, y_batch in data_loader:# 前向传播y_pred = model(X_batch)loss = loss_fn(y_pred, y_batch)# 反向传播optimizer.zero_grad()loss.backward()optimizer.step()if (epoch + 1) % 10 == 0:print(f'Epoch {epoch + 1}, Loss: {loss.item():.4f}')print(f'Estimated weight: {model.weight.item():.2f}, Estimated bias: {model.bias.item():.2f}')
3.7 模型评估
评估训练后的模型性能,并绘制预测结果:
import matplotlib.pyplot as plt# 使用训练后的模型进行预测
X_new = torch.tensor([[0], [2]]).float()
y_predict = model(X_new).detach().numpy()# 绘制数据和预测结果
plt.scatter(X, y, color='blue', label='True data')
plt.plot(X_new.numpy(), y_predict, color='red', linewidth=2, label='Fitted line')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression')
plt.legend()
plt.show()
3.8 完整代码
将上述代码整合在一起,可以直接运行以下代码来实现线性回归模型的简洁版:
import numpy as np
import torch
import torch.nn as nn
from torch.utils.data import TensorDataset, DataLoader
import matplotlib.pyplot as plt# 生成数据集
np.random.seed(42)
X = 2 * np.random.rand(100, 1) # 100个样本,每个样本1个特征
y = 4 + 3 * X + np.random.randn(100, 1) # 真实模型 y = 3x + 4 加上一些噪声# 转换为张量
X_tensor = torch.from_numpy(X).float()
y_tensor = torch.from_numpy(y).float()# 创建数据集和数据加载器
dataset = TensorDataset(X_tensor, y_tensor)
data_loader = DataLoader(dataset, batch_size=10, shuffle=True)# 定义模型
model = nn.Linear(1, 1) # 输入特征维度为1,输出维度为1# 初始化参数
nn.init.normal_(model.weight, mean=0, std=0.01)
nn.init.zeros_(model.bias)# 定义损失函数
loss_fn = nn.MSELoss()# 定义优化算法
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)# 训练模型
num_epochs = 100
for epoch in range(num_epochs):for X_batch, y_batch in data_loader:# 前向传播y_pred = model(X_batch)loss = loss_fn(y_pred, y_batch)# 反向传播optimizer.zero_grad()loss.backward()optimizer.step()if (epoch + 1) % 10 == 0:print(f'Epoch {epoch + 1}, Loss: {loss.item():.4f}')print(f'Estimated weight: {model.weight.item():.2f}, Estimated bias: {model.bias.item():.2f}')# 使用训练后的模型进行预测
X_new = torch.tensor([[0], [2]]).float()
y_predict = model(X_new).detach().numpy()# 绘制数据和预测结果
plt.scatter(X, y, color='blue', label='True data')
plt.plot(X_new.numpy(), y_predict, color='red', linewidth=2, label='Fitted line')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression')
plt.legend()
plt.show()
概念理解
- 简洁实现:使用PyTorch的高级API(如
nn.Linear、torch.optim)可以大大减少代码量,提高开发效率。 - 模型定义:
nn.Linear是PyTorch中定义线性层的模块,自动管理权重和偏置。 - 损失函数:使用PyTorch内置的
MSELoss,无需手动定义。 - 优化器:使用PyTorch的
torch.optim模块中的优化器(如SGD),自动更新模型参数。 - 训练过程:通过循环调用
DataLoader,自动处理数据的分批和随机打乱。
通过这种简洁实现,你可以更高效地构建和训练线性回归模型,同时利用PyTorch的强大功能来处理复杂的任务。
4 softmax回归
Softmax回归是用于多分类问题的线性模型。它通过Softmax函数将线性回归的输出转换为概率分布,从而实现多类分类。
4.1 Softmax回归的基本概念
概念理解:
Softmax回归适用于多分类问题,其中目标值是离散的类别。模型通过学习输入特征和类别之间的关系,预测每个类别的概率。
Softmax回归的模型形式为:
y ^ \hat{y} y^= s o f t m a x softmax softmax( X W + b XW + \mathbf{b} XW+b)
其中:
- X X X 是输入特征矩阵。
- W W W 是权重矩阵,每一列对应一个类别的权重向量。
- b \mathbf{b} b 是偏置向量,每个元素对应一个类别的偏置。
- y ^ \hat{y} y^ 是预测的类别概率分布。
Softmax函数的定义为:
softmax ( z ) i \text{softmax}(\mathbf{z})_i softmax(z)i = exp ( z i ) ∑ j = 1 K exp ( z j ) \frac{\exp(z_i)}{\sum_{j = 1}^{K} \exp(z_j)} ∑j=1Kexp(zj)exp(zi)
其中:
- z z z 是线性回归的输出。
- K K K 是类别的总数。
- softmax ( z ) i ) \text{softmax}(\mathbf{z})_i) softmax(z)i) 是第 i i i 个类别的概率。
4.2 Softmax回归的从零开始实现
4.2.1 生成数据集
为了演示,我们生成一个简单的多分类数据集,假设是一个三分类问题。
import numpy as np
import matplotlib.pyplot as plt# 生成数据集
np.random.seed(42)
X = np.random.rand(300, 2)
y = np.random.randint(0, 3, 300)# 绘制数据
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='red', label='Class 0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='blue', label='Class 1')
plt.scatter(X[y == 2][:, 0], X[y == 2][:, 1], color='green', label='Class 2')
plt.xlabel('X1')
plt.ylabel('X2')
plt.title('Generated Data')
plt.legend()
plt.show()
4.2.2 定义Softmax函数
Softmax函数将线性回归的输出转换为概率分布。
def softmax(z):exp_z = np.exp(z - np.max(z, axis=1, keepdims=True)) # 防止数值溢出return exp_z / np.sum(exp_z, axis=1, keepdims=True)
4.2.3 定义模型
Softmax回归模型的前向传播。
def model(X, W, b):return softmax(X @ W + b)
4.2.4 定义损失函数
Softmax回归使用交叉熵损失函数。
def cross_entropy_loss(y_pred, y_true):return -np.mean(np.log(y_pred[np.arange(len(y_true)), y_true]))
4.2.5 定义优化算法
使用随机梯度下降法更新模型参数。
def gradient_descent(X, y, W, b, learning_rate):y_pred = model(X, W, b)loss = cross_entropy_loss(y_pred, y)# 计算梯度m = len(X)y_one_hot = np.eye(3)[y] # 将标签转换为one-hot编码dW = X.T @ (y_pred - y_one_hot) / mdb = np.sum(y_pred - y_one_hot, axis=0) / m# 更新参数W -= learning_rate * dWb -= learning_rate * dbreturn loss
4.2.6 训练模型
训练Softmax回归模型。
# 初始化参数
W = np.random.randn(2, 3)
b = np.zeros(3)# 训练参数
learning_rate = 0.1
num_epochs = 100# 训练过程
losses = []
for epoch in range(num_epochs):loss = gradient_descent(X, y, W, b, learning_rate)losses.append(loss)if (epoch + 1) % 10 == 0:print(f'Epoch {epoch + 1}, Loss: {loss:.4f}')# 绘制损失曲线
plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Loss Curve')
plt.show()
4.3 Softmax回归的简洁实现
使用PyTorch的高级API来实现Softmax回归,更加简洁高效。
4.3.1 定义模型
使用PyTorch的 nn.Linear 和 nn.Softmax 定义模型。
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import TensorDataset, DataLoader# 转换为张量
X_tensor = torch.tensor(X, dtype=torch.float32)
y_tensor = torch.tensor(y, dtype=torch.long)# 创建数据集和数据加载器
dataset = TensorDataset(X_tensor, y_tensor)
data_loader = DataLoader(dataset, batch_size=32, shuffle=True)# 定义模型
model = nn.Sequential(nn.Linear(2, 3), # 输入特征维度为2,输出类别数为3nn.Softmax(dim=1) # 对输出应用Softmax函数
)# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)
4.3.2 训练模型
训练Softmax回归模型。
# 训练模型
num_epochs = 100
losses = []for epoch in range(num_epochs):for X_batch, y_batch in data_loader:# 前向传播y_pred = model(X_batch)loss = criterion(y_pred, y_batch)# 反向传播optimizer.zero_grad()loss.backward()optimizer.step()losses.append(loss.item())if (epoch + 1) % 10 == 0:print(f'Epoch {epoch + 1}, Loss: {loss.item():.4f}')# 绘制损失曲线
plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Loss Curve')
plt.show()
4.4 模型评估
评估训练后的模型性能,计算准确率。
# 计算准确率
model.eval() # 设置为评估模式
with torch.no_grad():y_pred = model(X_tensor)_, predicted = torch.max(y_pred, 1)accuracy = (predicted == y_tensor).sum().item() / len(y_tensor)print(f'Accuracy: {accuracy * 100:.2f}%')
4.5 完整代码
将上述代码整合在一起,可以直接运行以下代码来实现Softmax回归模型的简洁版:
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import TensorDataset, DataLoader
import matplotlib.pyplot as plt### 生成数据集
np.random.seed(42)
X = np.random.rand(300, 2)
y = np.random.randint(0, 3, 300)### 转换为张量
X_tensor = torch.tensor(X, dtype=torch.float32)
y_tensor = torch.tensor(y, dtype=torch.long)### 创建数据集和数据加载器
dataset = TensorDataset(X_tensor, y_tensor)
data_loader = DataLoader(dataset, batch_size=32, shuffle=True)### 定义模型
model = nn.Sequential(nn.Linear(2, 3), # 输入特征维度为2,输出类别数为3nn.Softmax(dim=1) # 对输出应用Softmax函数
)### 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)### 训练模型
num_epochs = 100
losses = []for epoch in range(num_epochs):for X_batch, y_batch in data_loader:# 前向传播y_pred = model(X_batch)loss = criterion(y_pred, y_batch)# 反向传播optimizer.zero_grad()loss.backward()optimizer.step()losses.append(loss.item())if (epoch + 1) % 10 == 0:print(f'Epoch {epoch + 1}, Loss: {loss.item():.4f}')### 绘制损失曲线
plt.plot(losses)
plt
相关文章:
动手学线性神经网络:从数学原理到代码实现)
(三)动手学线性神经网络:从数学原理到代码实现
1 线性回归 线性回归是一种基本的预测模型,用于根据输入特征预测连续的输出值。它是机器学习和深度学习中最简单的模型之一,但却是理解更复杂模型的基础。 1.1 线性回归的基本元素 概念理解: 线性回归假设输入特征和输出之间存在线性关系。…...
Axure形状类组件图标库(共8套)
点击下载《月下倚楼图标库(形状组件)》 原型效果:https://axhub.im/ax9/02043f78e1b4386f/#g1 摘要 本图标库集锦精心汇集了8套专为Axure设计的形状类图标资源,旨在为产品经理、UI/UX设计师以及开发人员提供丰富多样的设计素材,提升原型设计…...

20250530-C#知识:String与StringBuilder
String与StringBuilder string字符串在开发中经常被用到,不过在需要频繁对字符串进行增加和删除时,使用StringBuilder有利于提升效率。 1、String string是一种引用类型而非值类型(某些方面像值类型)使用“”进行两个string对象的…...

从 Docker 到 Containerd:Kubernetes 容器运行时迁移实战指南
一、背景 Kubernetes 自 v1.24 起移除了 dockershim,不再原生支持 Docker Engine,用户需迁移至受支持的 CRI 兼容运行时,如: Containerd(推荐,高性能、轻量级) CRI-O(专为 Kuberne…...

uniapp中view标签使用范围
不止用于微信小程序。兼容型号,是uniapp内置组件之一,在uniapp中进行了跨平台适配。支持所有uniapp的平台。如微信小程序、h5、app、支付宝小程序...

Celery 核心概念详解及示例
Celery 核心概念详解及示例 Celery 是一个简单、灵活且可靠的分布式系统,用于处理大量消息,提供对任务队列的操作,并支持任务的调度和异步执行。它常用于深度优化 Web 应用的性能和响应速度,通过将耗时的操作移到后台异步执行&am…...

欢乐熊大话蓝牙知识14:用 STM32 或 EFR32 实现 BLE 通信模块:从0到蓝牙,你也能搞!
🚀 用 STM32 或 EFR32 实现 BLE 通信模块:从0到蓝牙,你也能搞! “我能不能自己用 STM32 或 EFR32 实现一个 BLE 模块?” 答案当然是:能!还能很帅! 👨🏭 前…...

IDEA 在公司内网配置gitlab
赋值项目链接 HTTPS 将HTTP的链接 ip地址换成 内网地址 例如:https:172.16.100.18/...... 如果出现需要需要Token验证的情况: 参考:Idea2024中拉取代码时GitLab提示输入token的问题_gitlab token-CSDN博客...

黑马Java面试笔记之 微服务篇(业务)
一. 限流 你们项目中有没有做过限流?怎么做的? 为什么要限流呢? 一是并发的确大(突发流量) 二是防止用户恶意刷接口 限流的实现方式: Tomcat:可以设置最大连接数 可以通过maxThreads设置最大Tomcat连接数,实现限流,但是适用于单体架构 Nginx:漏桶算法网关,令牌桶算法自定…...

通过WiFi无线连接小米手机摄像头到电脑的方法
通过WiFi无线连接小米手机摄像头到电脑的方法 以下是基于Scrcpy和DroidCam两种工具的无线连接方案,需提前完成开发者模式与USB调试的开启(参考原教程步骤): 方法一:Scrcpy无线投屏(无需手机端安装…...

长短期记忆(LSTM)网络模型
一、概述 长短期记忆(Long Short-Term Memory,LSTM)网络是一种特殊的循环神经网络(RNN),专门设计用于解决传统 RNN 在处理长序列数据时面临的梯度消失 / 爆炸问题,能够有效捕捉长距离依赖关系。…...

深入理解 Linux 文件系统与日志文件分析
一、Linux 文件系统概述 1. 文件系统的基本概念 文件系统(File System)是操作系统用于管理和组织存储设备上数据的机制。它提供了一种结构,使得用户和应用程序能够方便地存储和访问数据。 2. Linux 文件系统结构 Linux 文件系统采用树状目…...

CSS3美化页面元素
1. 字体 <span>标签 字体样式⭐ 字体类型(font-family) 字体大小(font-size) 字体风格(font-style) 字体粗细(font-weight) 字体属性(font) 2. 文本 文…...
3-0 等级保护测评要求现行技术标准)
网络安全-等级保护(等保)3-0 等级保护测评要求现行技术标准
################################################################################ 第三章:测评要求、测评机构要求,最终目的是通过测评,所以我们将等保要求和测评相关要求一一对应形成表格。 GB/T 28448-2019 《信息安全技术 网络安全等…...

WPS 利用 宏 脚本拆分 Excel 多行文本到多行
文章目录 WPS 利用 宏 脚本拆分 Excel 多行文本到多行效果需求背景🛠 操作步骤代码实现代码详解使用场景注意事项总结 WPS 利用 宏 脚本拆分 Excel 多行文本到多行 在 Excel 工作表中,我们经常遇到一列中包含多行文本(用换行符分隔ÿ…...

R语言错误处理方法大全
在R语言的批量运行中,常需要自动跳过错误,继续向下运行。 1、使用 tryCatch() 捕获错误并返回占位符 # 示例:循环中跳过错误继续执行 results <- numeric(5) # 预分配结果向量for(i in 1:5) {# 用 tryCatch 包裹可能出错的代码results[…...

AI“实体化”革命:具身智能如何重构体育、工业与未来生活
近年来,人工智能(AI)技术的飞速发展正在重塑各行各业,而具身智能(Embodied AI)作为AI领域的重要分支,正逐渐从实验室走向现实应用。具身智能的核心在于让AI系统具备物理实体,能够与环…...

Opencv4 c++ 自用笔记 05 形态学操作
图像形态学主要获取物体的形状与位置信息。利用具有一定形态的结构元素度量和提取图像中的对应形状,达到对图像分析和识别的目的。操作主要包括腐蚀、膨胀、开运算和闭运算。 像素距离与连通域 图像形态学中,将不与其他区域链接的独立区域称为集合或者…...

DrissionPage 数据提取技巧全解析:从入门到实战
在当今数据驱动的时代,网页数据提取已成为自动化办公、市场分析和爬虫开发的核心技能。作为新一代网页自动化工具,DrissionPage 以其独特的双模式融合设计(Selenium Requests)脱颖而出。本文将结合官方文档与实战案例,…...

如何构建自适应架构的镜像
目标 我有一个服务叫xxx,一开始它运行在x86架构的机器上,所以最开始有个xxx:stable-amd64的镜像,后来它又需要运行在arm64架构的机器上,所以又重新打了个xxx:stable-arm64的镜像 但是对于安装脚本来说,我不希望我在拉…...

R语言基础| 创建数据集
在R语言中,有多种数据类型,用以存储和处理数据。每种数据类型都有其特定的用途和操作函数,使得R语言在处理各种数据分析任务时非常灵活和强大: 向量(Vector): 向量是R语言中最基本的数据类型,它…...

剑指offer15_数值的整数次方
数值的整数次方 实现函数 double Power(double base, int exponent) 题目要求 计算 base exponent \text{base}^{\text{exponent}} baseexponent: 不得使用库函数不需要考虑大数问题,绝对误差不超过 10 − 2 10^{-2} 10−2不会出现底数和指数同为 0…...

Centos7搭建zabbix6.0
此方法适用于zabbix6以上版本zabbix6.0前期环境准备:Lamp(linux httpd mysql8.0 php)mysql官网下载位置:https://dev.mysql.com/downloads/mysql/Zabbix源码包地址:https://www.zabbix.com/cn/download_sourcesZabbix6…...

使用Redis的四个常见问题及其解决方案
Redis 缓存穿透 定义:redis查询一个不存在的数据,导致每次都查询数据库 解决方案: 如果查询的数据为空,在redis对应的key缓存空数据,并设置短TTL。 因为缓存穿透通常是因为被恶意用不存在的查询参数进行压测攻击&…...

Docker 部署前后端分离项目
1.Docker 1.1 什么是 Docker ? Docker 是一种开源的 容器化平台,用于开发、部署和运行应用程序。它通过 容器(Container) 技术,将应用程序及其依赖项打包在一个轻量级、可移植的环境中,确保应用在不同计算…...

云游戏混合架构
云游戏混合架构通过整合本地计算资源与云端能力,形成了灵活且高性能的技术体系,其核心架构及技术特征可概括如下: 一、混合架构的典型模式 分层混合模式 前端应用部署于公有云(如渲染流化服务),后端逻辑…...

【小红书】API接口,获取笔记核心数据
小红书笔记核心数据API接口详解 - 深圳小于科技提供专业数据服务 深圳小于科技(官网:https://www.szlessthan.com)推出的小红书笔记核心数据API接口,为开发者提供精准的笔记互动数据分析能力,助力内容运营与商业决策。…...

会议室钥匙总丢失?换预约功能的智能门锁更安全
在企业日常运营中,会议室作为重要的沟通与协作场所,其管理效率与安全性直接影响着企业的运作顺畅度。然而,传统会议室管理方式中钥匙丢失、管理不便等问题频发,给企业带来了不少困扰。近期,某企业引入了启辰智慧预约系…...
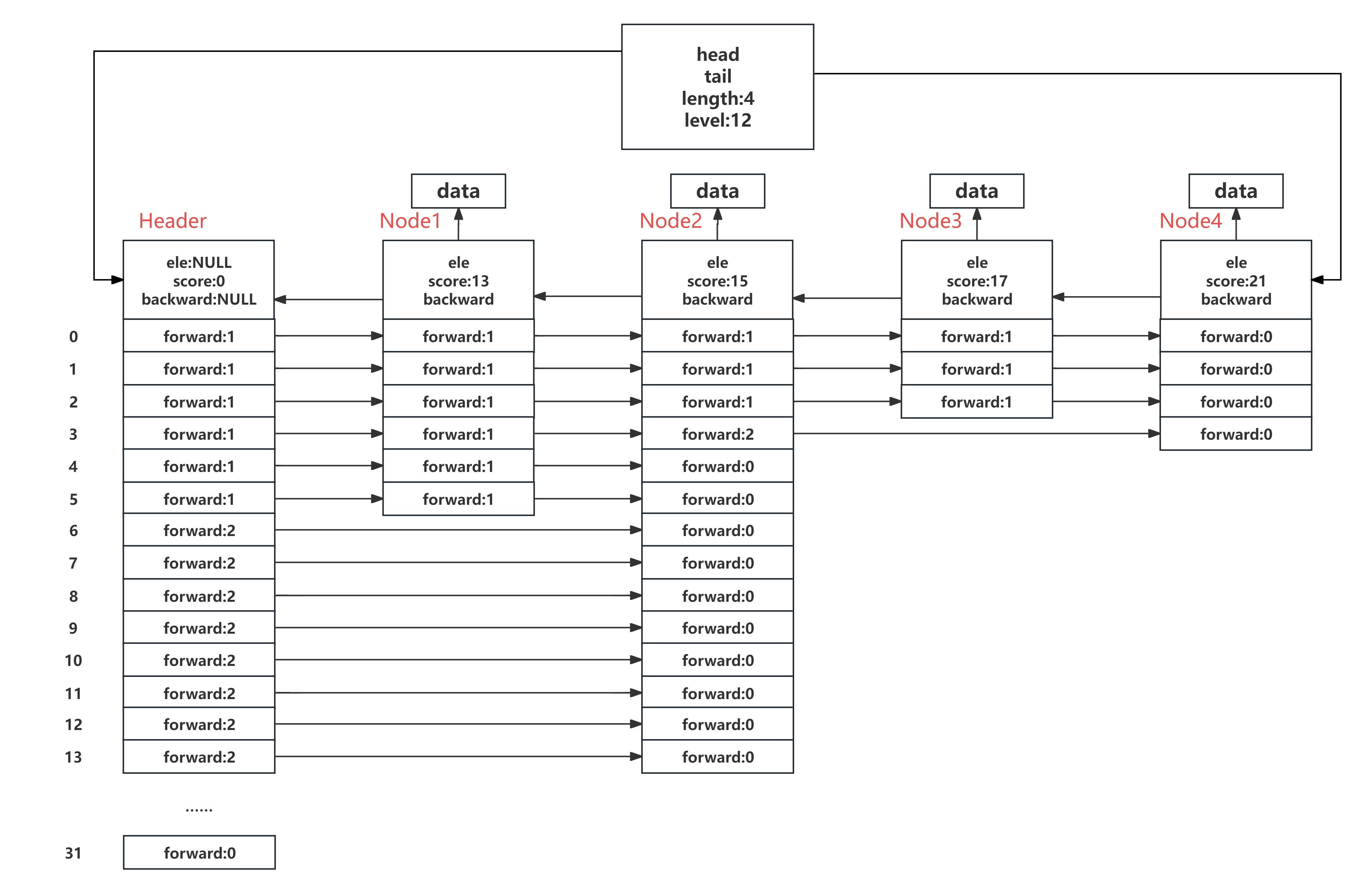
Redis底层数据结构之跳表(SkipList)
SkipList是Redis有序结合ZSet底层的数据结构,也是ZSet的灵魂所在。与之相应的,Redis还有一个无序集合Set,这两个在底层的实现是不一样的。 标准的SkipList: 跳表的本质是一个链表。链表这种结构虽然简单清晰,但是在查…...

跨架构镜像打包问题及解决方案
问题背景: 需求: 有一个镜像是 docker.io 的,是 docker.io/aquasec/kube-bench:v0.10.6,我想把该镜像在本地电脑(可翻墙)下载下来,然后 docker save 打包成一个 tar 包,传输到服务器…...
