基于MATLAB的FTN调制和硬判决的实现
在数字通信中,FTN(Full-Transmit-Null)是一种调制技术,用于在有限带宽的信道中传输数据。FTN调制通过在符号之间插入零值,使得频谱在符号速率的整数倍处为零,从而减少频谱重叠。硬判决是一种简单的解调方式,根据接收信号的幅度或相位直接判断符号。
基于MATLAB的FTN调制和硬判决的实现示例,包括不同压缩因子(如0.8、0.7、1)的影响。
1. FTN调制
FTN调制通过在符号之间插入零值来实现。压缩因子(shadow factor)决定了符号之间的零值数量。压缩因子为1表示没有压缩,符号之间没有插入零值;压缩因子小于1表示有压缩,符号之间插入零值。
1.1 生成FTN调制信号
function [tx_signal, tx_signal_compressed] = ftn_modulate(data, M, shadow_factor)% 参数:% data: 输入数据,一个行向量% M: 调制阶数(例如,M=4表示QPSK)% shadow_factor: 压缩因子(例如,0.8、0.7、1)% 将数据映射到星座点constellation = exp(1j * 2 * pi * (0:M-1) / M);tx_signal = constellation(data);% 插入零值以实现FTN调制num_zeros = floor(1 / shadow_factor) - 1;tx_signal_compressed = zeros(1, length(tx_signal) * (num_zeros + 1));tx_signal_compressed(1:1+num_zeros:end) = tx_signal;
end
2. 硬判决
硬判决是一种简单的解调方式,根据接收信号的幅度或相位直接判断符号。FTN传输端的发送以及硬判决,含有发送波形不同压缩影子0.8 0.7 1
2.1 硬判决解调
function demodulated_data = hard_decision(rx_signal, M)% 参数:% rx_signal: 接收信号% M: 调制阶数(例如,M=4表示QPSK)% 生成星座点constellation = exp(1j * 2 * pi * (0:M-1) / M);% 硬判决解调demodulated_data = zeros(1, length(rx_signal));for i = 1:length(rx_signal)[~, idx] = min(abs(rx_signal(i) - constellation));demodulated_data(i) = idx - 1;end
end
3. 仿真示例
以下是一个完整的仿真示例,包括FTN调制、信道传输和硬判决解调。
3.1 生成随机数据
% 参数设置
M = 4; % 调制阶数(QPSK)
data_length = 1000; % 数据长度
shadow_factors = [0.8, 0.7, 1]; % 压缩因子% 生成随机数据
data = randi([0, M-1], 1, data_length);
3.2 FTN调制
% 初始化发送信号
tx_signals = cell(1, length(shadow_factors));% 对每个压缩因子进行FTN调制
for i = 1:length(shadow_factors)[tx_signal, tx_signal_compressed] = ftn_modulate(data, M, shadow_factors(i));tx_signals{i} = tx_signal_compressed;
end
3.3 信道传输
假设信道是加性高斯白噪声(AWGN)信道。
% 信道噪声
snr_db = 20; % 信噪比(dB)
rx_signals = cell(1, length(shadow_factors));
for i = 1:length(shadow_factors)rx_signals{i} = awgn(tx_signals{i}, snr_db, 'measured');
end
3.4 硬判决解调
% 初始化解调数据
demodulated_data = cell(1, length(shadow_factors));% 对每个接收信号进行硬判决解调
for i = 1:length(shadow_factors)demodulated_data{i} = hard_decision(rx_signals{i}, M);
end
3.5 计算误码率
% 计算误码率
ber = zeros(1, length(shadow_factors));
for i = 1:length(shadow_factors)ber(i) = sum(data ~= demodulated_data{i}(1:data_length)) / data_length;
end% 显示结果
disp('误码率:');
disp(ber);
4. 结果分析
通过上述仿真,可以观察到不同压缩因子对误码率的影响。通常,压缩因子越小,符号之间的零值越多,频谱重叠越少,误码率越低。然而,压缩因子越小,频谱效率也越低。
5. 可视化
绘制发送信号和接收信号的波形,以便直观观察FTN调制和信道传输的效果。
5.1 绘制波形
% 绘制发送信号和接收信号
figure;
for i = 1:length(shadow_factors)subplot(length(shadow_factors), 2, 2*i-1);plot(real(tx_signals{i}));title(['发送信号,压缩因子 = ', num2str(shadow_factors(i))]);xlabel('样本');ylabel('实部');subplot(length(shadow_factors), 2, 2*i);plot(real(rx_signals{i}));title(['接收信号,压缩因子 = ', num2str(shadow_factors(i))]);xlabel('样本');ylabel('实部');
end
通过上述步骤,可以实现FTN调制和硬判决解调,并分析不同压缩因子对误码率的影响。希望这个示例对你有所帮助。如果有任何问题或需要进一步的帮助,请随时提问。
相关文章:

基于MATLAB的FTN调制和硬判决的实现
在数字通信中,FTN(Full-Transmit-Null)是一种调制技术,用于在有限带宽的信道中传输数据。FTN调制通过在符号之间插入零值,使得频谱在符号速率的整数倍处为零,从而减少频谱重叠。硬判决是一种简单的解调方式…...

涂装协作机器人:重新定义涂装工艺的智能化未来
一、涂装场景的产业变革与核心诉求 1.1 千亿级市场的技术突围战 在汽车制造领域,涂装车间被称为"工业化妆间",其工艺质量直接影响产品溢价能力。当前行业面临三重挑战: 质量维度:传统人工喷涂存在膜厚波动15μm的行业…...

c++面向对象第4天---拷贝构造函数与深复制
含有对象成员的构造函数深复制与浅复制拷贝(复制)构造函数 第一部分:含有对象成员的构造函数 以下是一个学生 类包含日期成员出生日期的代码 #include<iostream> using namespace std; class Date { public:Date(int year,int month…...

Windows版PostgreSQL 安装 vector 扩展
问题 spring-ai在集成PGVector向量存储的时候会报错如下,那么就需要安装pgsql的vector扩展。 SQL [CREATE EXTENSION IF NOT EXISTS vector]; 错误: 无法打开扩展控制文件 "C:/Program Files/PostgreSQL/9.6/share/extension/vector.control": No such …...
KINGCMS被入侵
现象会强制跳转到 一个异常网站,请掉截图代码. 代码中包含经过混淆处理的JavaScript,它使用了一种技术来隐藏其真实功能。代码中使用了eval函数来执行动态生成的代码,这是一种常见的技术,恶意脚本经常使用它来隐藏其真实目的。 这段脚本会检…...

完美解决在pycharm中创建Django项目安装mysqlclient报错的问题(windows下)
正常情况下,在Windows安装mysqlclient会报错: 我这里用的是anaconda虚拟环境,安装前必须激活anacoda虚拟环境, 怎么激活虚拟环境?可以参考超详细的pycharmanaconda搭建python虚拟环境_pycharm anaconda环境搭建-CSDN博…...
『React』组件副作用,useEffect讲解
在 React 开发中,有时候会听到“副作用”这个词。特别是用到 useEffect 这个 Hook 的时候,官方就明确说它是用来处理副作用的。那什么是副作用?为什么我们要专门管控它?今天就聊聊 React 中的组件副作用。 📌 什么是“…...

使用VSCode在WSL和Docker中开发
通过WSL,开发人员可以安装 Linux 发行版(例如 Ubuntu、OpenSUSE、Kali、Debian、Arch Linux 等),并直接在 Windows 上使用 Linux 应用程序、实用程序和 Bash 命令行工具,不用进行任何修改,也无需使用传统虚…...

ZooKeeper 命令操作
文章目录 Zookeeper 数据模型Zookeeper 服务端常用命令Zookeeper 客户端常用命令 Zookeeper 数据模型 ZooKeeper 是一个树形目录服务,其数据模型和Unix的文件系统目录树很类似,拥有一个层次化结构。这里面的每一个节点都被称为: ZNode,每个节…...

解决 Ubuntu 20.04 虚拟机中 catkin_make 编译卡死问题
完整解决步骤 1. 禁用当前交换文件 sudo swapoff /swapfile 2. 删除旧的交换文件 sudo rm /swapfile 3. 使用更可靠的创建方法 # 使用 dd 命令创建交换文件(更兼容但较慢) sudo dd if/dev/zero of/swapfile bs1M count4096# 或者使用 truncate 命令…...

【HTML-15】HTML表单:构建交互式网页的基石
表单是HTML中最强大的功能之一,它允许网页收集用户输入并与服务器进行交互。无论是简单的搜索框、登录页面,还是复杂的多步骤调查问卷,表单都是实现这些功能的核心元素。本文将深入探讨HTML表单的各个方面,帮助您构建高效、用户友…...

一些较好的学习方法
1、网上有一些非常经典的电路,而且有很多视频博主做了详细的讲解。 2、有一部分拆解的UP主,拆解后会还原该器件的原理图,并一步步做讲解。 3、有两本书,数电、模电,这两本书中的内容很多都值得学习。 5、某宝上卖的…...
Redis底层数据结构之深入理解跳表(1)
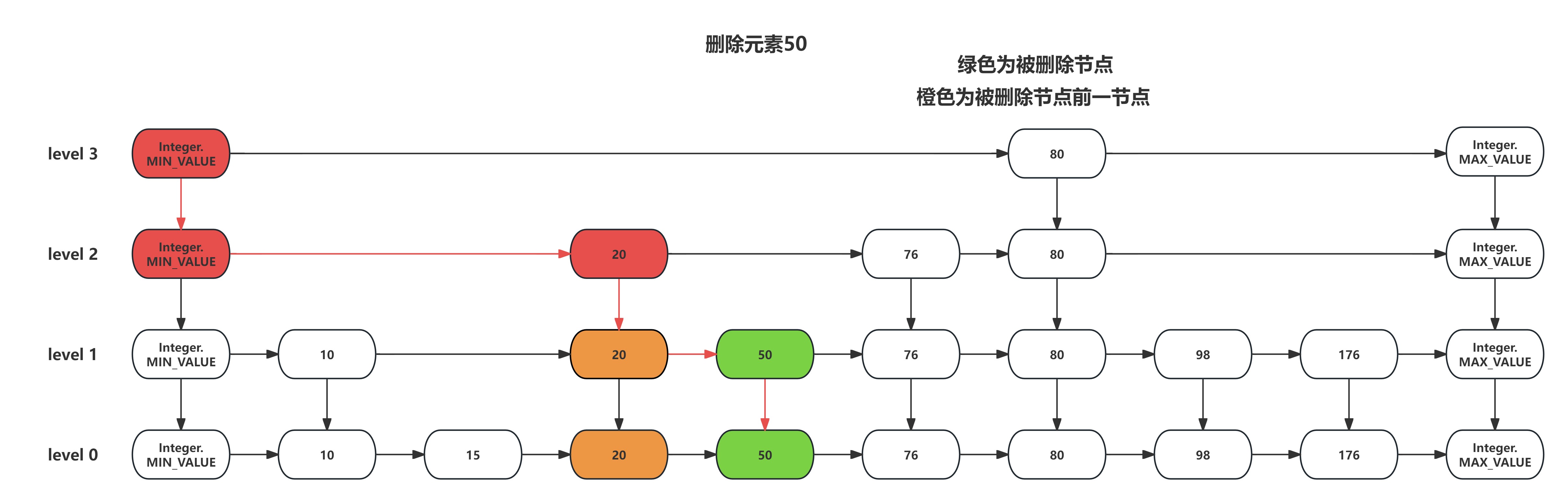
在上一篇文章中我们详细的介绍了一下Redis中跳表的结构以及为什么Redis要引入跳表而不是平衡树或红黑树。这篇文章我们就来详细梳理一下跳表的增加、搜索和删除步骤。 SkipList的初始化 跳表初始化时,将每一层链表的头尾节点创建出来并使用集合将头尾节点进行存储&…...
的实战教程)
鸿蒙【HarmonyOS 5】 (React Native)的实战教程
一、环境配置 安装鸿蒙专属模板 bashCopy Code npx react-native0.72.5 init HarmonyApp --template react-native-template-harmony:ml-citation{ref"4,6" data"citationList"} 配置 ArkTS 模块路径 在 entry/src/main/ets 目录下创建原生模块&…...

PCB设计教程【入门篇】——电路分析基础-元件数据手册
前言 本教程基于B站Expert电子实验室的PCB设计教学的整理,为个人学习记录,旨在帮助PCB设计新手入门。所有内容仅作学习交流使用,无任何商业目的。若涉及侵权,请随时联系,将会立即处理 目录 前言 一、数据手册的重要…...

20250529-C#知识:继承、密封类、密封方法、重写
C#知识:继承、密封类、密封方法、重写 继承是面向对象的三大特性之一,通过继承能够减少重复代码的编写,有助于提升开发效率。 1、继承 C#不同于C,只支持单继承当子类出现与父类同名的成员时,父类成员被隐藏࿰…...

从0到1,带你走进Flink的世界
目录 一、Flink 是什么? 二、Flink 能做什么? 三、Flink 架构全景概览 3.1 分层架构剖析 3.2 核心组件解析 四、Flink 的核心概念 4.1 数据流与数据集 4.2 转换操作 4.3 窗口 4.4 时间语义 4.5 状态与检查点 五、Flink 安装与快速上手 5.1 …...

springboot @value
#springboot value value 可以读取 yaml 中 的数据...

Dify-5:Web 前端架构
本文档提供了 Dify Web 前端架构的技术概述,包括核心组件、结构和关键技术。它解释了前端如何组织、组件如何通信以及国际化功能如何实现。 技术栈 Dify 的 Web 前端基于现代 JavaScript 技术栈构建: 框架:Next.js(基于 React …...

深度学习赋能图像识别:技术、应用与展望
论文: 一、引言 1.1 研究背景与意义 在当今数字化时代,图像作为信息的重要载体,广泛存在于各个领域。图像识别技术旨在让计算机理解和识别图像内容,将图像中的对象、场景、行为等信息转化为计算机能够处理的符号或数据 &am…...

八N皇后问题
1 问题的提出 在8X8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法 我们的任务就是用MATLAB进行求解 2 数学模型的构建 首先我们分析题目就是 任意两个皇后都不能处于…...

TMS320F28388D使用sysconfig配置IPC
第1章 配置IPC底层代码 使用IPC的动机: 我计划我的项目中要使用RS485,CANFD通信和EtherCAT通信,由于通信种类较多,而对于电机控制来说大部分数据都是重复的,并且有些数据可以很久才改变一次,所以我计划使…...
轮转数组)
代码训练LeetCode(19)轮转数组
代码训练(19)LeetCode之轮转数组 Author: Once Day Date: 2025年6月3日 漫漫长路,才刚刚开始… 全系列文章可参考专栏: 十年代码训练_Once-Day的博客-CSDN博客 参考文章: 189. 轮转数组 - 力扣(LeetCode)力扣 (LeetCode) 全球极客挚爱的…...

每日算法 -【Swift 算法】将整数转换为罗马数字
💡 Swift:将整数转换为罗马数字(含思路讲解与详细注释) 罗马数字是一种古老的数字表示方式,虽然在现代我们不再使用它进行计算,但在表盘、章节、纪念碑等地方依然很常见。今天我们就来实现一个经典算法题&…...

Qwen与Llama分词器核心差异解析
Qwen和 Llama 词映射(分词器)的区别及通用词映射逻辑 一、Qwen 与 Llama 词映射(分词器)区别 维度Qwen 分词器Llama 分词器技术基础基于字节级别字节对编码(BBPE),以 cl100k 为基础词库,扩充中文字词、多语言词汇基于 BPE,但依赖 SentencePiece 单字模型,核心为英文优…...

华为云Flexus+DeepSeek征文 | 基于ModelArts Studio 与 Cline 快速构建AI编程助手
目录 一、前言 二、ModelArts Studio(MaaS)介绍与应用场景 2.1ModelArts Studio(MaaS)介绍 2.2 ModelArts Studio(MaaS)使用场景 2.3 开通MaaS服务 2.4 开通DeepSeek-V3商用服务 三、Cline简介和安装 3.1 C…...

pikachu靶场通关笔记11 XSS关卡07-XSS之关键字过滤绕过(三种方法渗透)
目录 一、源码分析 1、进入靶场 2、代码审计 3、攻击思路 二、渗透实战 1、探测过滤信息 2、注入Payload1 3、注入Payload2 4、注入Payload3 本系列为通过《pikachu靶场通关笔记》的XSS关卡(共10关)渗透集合,通过对XSS关卡源码的代码审计找到安…...

Android App引用vendor编写的jni动态库
简单描述一下,就是我自己基于FastDDS写了一个Jni的so,然后编写了jar包引用该so,最后写了一个Android的测试apk使用jar包,调用jni中的接口去创建Participant,Subscriber等。 实际将jni的so放到 /system_ext/lib64&#…...

React从基础入门到高级实战:React 核心技术 - 错误处理与错误边界:构建稳定的应用
React 错误处理与错误边界:构建稳定的应用 在开发 React 应用时,错误处理是确保应用稳定性和用户体验的重要环节。无论是运行时错误、API 请求失败还是用户操作失误,合理的错误处理机制都能防止应用崩溃,并为用户提供清晰友好的反…...
与后台数据库进行交互时常用的两种方式)
页面输入数据的表格字段(如 Web 表单或表格控件)与后台数据库进行交互时常用的两种方式
“从页面输入数据的表格字段(如 Web 表单或表格控件)在与后台数据库进行交互时,常用的有两种方式:” 🎯 两种方式(操作调用数据库、绑定数据) 🚀 方式1:前端代码提交数据到后端,再由后端调用数据库 💡 原理和逻辑: 用户在页面上(比如输入表单、表格)输入数据…...
