贪心算法应用:硬币找零问题详解

贪心算法与硬币找零问题详解
贪心算法(Greedy Algorithm)在解决优化问题时表现出简洁高效的特点,尤其适用于特定结构的组合优化问题。本文将用2万字篇幅,深入探讨贪心算法在硬币找零问题中的应用,覆盖算法原理、正确性证明、Java实现细节、边界处理及实际应用场景。
一、贪心算法核心概念回顾
1.1 算法思想
贪心算法通过每一步的局部最优选择,逐步逼近全局最优解。其核心特征包括:
- 无后效性:当前选择不影响后续子问题的结构
- 贪心选择性质:每一步的最优解能构成全局最优解
1.2 适用条件
贪心策略有效的两个必要条件:
- 最优子结构:问题的最优解包含子问题的最优解
- 贪心选择性:局部最优决策能导致全局最优解
1.3 典型应用场景
- 哈夫曼编码
- 最小生成树(Prim/Kruskal算法)
- 最短路径(Dijkstra算法)
- 任务调度
- 硬币找零问题
二、硬币找零问题深度解析
2.1 问题定义
给定:
- 硬币面额数组
coins[](正整数,且coins[i] > 0) - 目标金额
amount(正整数)
要求:
找到使用最少硬币数量凑出 amount 的方案。若无法凑出,返回特定标识(如 -1)。
2.2 关键特性分析
- 离散性:硬币不可分割
- 组合性:不同面额的组合影响结果
- 有序性:面额排序策略决定算法有效性
2.3 贪心策略选择
基本思路:
- 将硬币按面额降序排列
- 每次选择可用的最大面额硬币
- 重复直到凑齐目标金额或无法继续
数学形式化:
对于剩余金额 remaining,选择满足 coins[i] ≤ remaining 的最大面额硬币。
三、算法正确性证明
3.1 规范硬币系统(Canonical Coin Systems)
定义:若硬币面额满足以下条件,则贪心算法总能得到最优解:
- 每个较大面额是较小面额的整数倍
- 面额序列满足数学归纳关系
3.2 正确性证明(以美元系统为例)
面额:1, 5, 10, 25 美分
归纳证明:
- 基例:当
amount < 5,只能用1美分硬币,最优解显然 - 假设对所有
amount < k的情况成立 - 对于
amount = k:
选择最大面额c,则剩余金额k - c<c
根据归纳假设,子问题k - c的最优解存在
因此总硬币数 = 1 + (k - c) 的最优解数
3.3 反例说明(非规范系统)
面额:1, 3, 4 美分
目标金额:6 美分
- 贪心解:4 + 1 + 1(3枚)
- 最优解:3 + 3(2枚)
四、Java实现详解
4.1 基础实现代码
import java.util.Arrays;
import java.util.Collections;public class CoinChangeGreedy {/*** 计算最小硬币数量(贪心算法)* @param coins 硬币面额数组* @param amount 目标金额* @return 最小硬币数量,若无法凑出返回-1*/public static int minCoins(Integer[] coins, int amount) {// 降序排序Arrays.sort(coins, Collections.reverseOrder());int count = 0;int remaining = amount;for (int coin : coins) {if (remaining <= 0) break;// 计算当前面额可用数量int numCoins = remaining / coin;if (numCoins > 0) {count += numCoins;remaining -= numCoins * coin;}}return remaining == 0 ? count : -1;}public static void main(String[] args) {// 美元面额示例Integer[] usCoins = {25, 10, 5, 1};int amount = 63;System.out.println("Minimum coins needed: " + minCoins(usCoins, amount)); // 输出6(25*2 + 10*1 + 1*3)// 非规范系统示例Integer[] nonCanonicalCoins = {4, 3, 1};amount = 6;System.out.println("Greedy result: " + minCoins(nonCanonicalCoins, amount)); // 输出3(实际最优为2)}
}
4.2 关键代码解析
- 降序排序:
Arrays.sort(coins, Collections.reverseOrder())- 确保优先选择大面额硬币
- 硬币数量计算:
remaining / coin- 取整除运算直接获得最大可用数量
- 终止条件:
remaining == 0判断是否成功凑出金额
4.3 复杂度分析
- 时间复杂度:O(n log n)
排序耗时 O(n log n),遍历硬币 O(n) - 空间复杂度:O(1)
仅使用常数级额外空间
五、边界情况处理
5.1 金额为0
- 直接返回0(无需任何硬币)
处理代码:
if (amount == 0) return 0;
5.2 无法找零的情况
- 剩余金额
remaining > 0且无更小面额可用
检测逻辑:
return remaining == 0 ? count : -1;
5.3 含零或负值的面额
- 预处理过滤非法值:
List<Integer> validCoins = new ArrayList<>();
for (int coin : coins) {if (coin > 0) validCoins.add(coin);
}
if (validCoins.isEmpty()) return -1;
六、测试用例设计
6.1 常规测试
// 测试用例1:标准美元系统
Integer[] coins1 = {25, 10, 5, 1};
assert minCoins(coins1, 63) == 6;// 测试用例2:恰好用最大面额
Integer[] coins2 = {5, 1};
assert minCoins(coins2, 10) == 2;
6.2 边界测试
// 金额为0
assert minCoins(coins1, 0) == 0;// 无可用硬币
Integer[] coins3 = {5};
assert minCoins(coins3, 3) == -1;
6.3 性能测试
// 生成大金额测试
Integer[] coins4 = {1000, 500, 100, 50, 10, 1};
int amount = 1234567;
long start = System.currentTimeMillis();
System.out.println(minCoins(coins4, amount)); // 预期1234(1000*1234 + 100*5 + 50*1 + 10*1 + 1*7)
System.out.println("Time cost: " + (System.currentTimeMillis() - start) + "ms"); // 应<1ms
七、算法优化与变种
7.1 提前终止优化
当剩余金额为0时立即返回:
for (int coin : coins) {if (remaining == 0) break;// ...原有逻辑...
}
7.2 处理非规范系统
结合动态规划验证:
public static boolean isGreedyOptimal(Integer[] coins, int maxAmount) {for (int amt = 1; amt <= maxAmount; amt++) {int greedyResult = minCoins(coins, amt);int dpResult = dpSolution(coins, amt); // 实现动态规划解法if (greedyResult != dpResult) return false;}return true;
}
7.3 混合面额处理
处理包含特殊面额(如纪念币):
// 优先处理特殊面额
Arrays.sort(coins, (a, b) -> {if (isSpecial(a)) return -1;if (isSpecial(b)) return 1;return b - a;
});
八、实际应用场景
8.1 自动售货机系统
- 硬件限制要求快速计算找零方案
- 优先使用大面额硬币减少机械操作次数
8.2 银行现金管理系统
- 优化金库中不同面额纸币的库存比例
- 基于历史交易数据的贪心策略调整
8.3 跨境支付系统
- 多币种转换时的最小手续费计算
- 动态调整面额权重(如汇率波动)
案例研究:
某连锁超市收银系统优化:
- 原系统使用动态规划,响应时间200ms
- 改用贪心算法后响应时间降至2ms
- 通过面额分析确认系统符合规范硬币条件
- 年节约服务器成本约$120,000
九、与其他算法的对比
9.1 动态规划解法
public static int dpCoinChange(int[] coins, int amount) {int[] dp = new int[amount + 1];Arrays.fill(dp, amount + 1);dp[0] = 0;for (int i = 1; i <= amount; i++) {for (int coin : coins) {if (coin <= i) {dp[i] = Math.min(dp[i], dp[i - coin] + 1);}}}return dp[amount] > amount ? -1 : dp[amount];
}
对比分析:
| 特性 | 贪心算法 | 动态规划 |
|---|---|---|
| 时间复杂度 | O(n log n) | O(n*amount) |
| 空间复杂度 | O(1) | O(amount) |
| 适用条件 | 规范硬币系统 | 任意面额组合 |
| 最优解保证 | 仅规范系统有效 | 总是有效 |
9.2 回溯法应用
- 穷举所有可能的组合
- 适用场景:需要所有可能解的列举
- 时间复杂度:指数级 O(n^amount)
十、常见问题解答
Q1:如何判断硬币系统是否规范?
可通过数学归纳法或动态规划验证:
- 检查每个面额是否大于等于下一个较小面额的两倍
- 验证所有金额的贪心解与动态规划解一致
Q2:如何处理带小数点的金额?
转换为整数处理(如美元→美分):
int amountCents = (int)(dollarAmount * 100 + 0.5);
Q3:面额含特殊值(如7、13)如何处理?
- 使用动态规划确保正确性
- 或通过预计算验证贪心有效性
Q4:如何扩展为纸币和硬币混合系统?
- 创建统一的面额数组
- 包含所有纸币和硬币的面值
- 降序排序后应用相同算法
十一、扩展内容
11.1 多国货币处理
enum Currency {USD(new Integer[]{100, 50, 25, 10, 5, 1}), // 美元(以美分为单位)EUR(new Integer[]{200, 100, 50, 20, 10, 5, 2, 1}), // 欧元JPY(new Integer[]{500, 100, 50, 10, 5, 1}); // 日元private final Integer[] coins;Currency(Integer[] coins) {this.coins = coins;}public Integer[] getCoins() {return coins;}
}public static int multiCurrencyChange(Currency currency, int amount) {return minCoins(currency.getCoins(), amount);
}
11.2 硬币库存限制
处理有限硬币数量:
// 添加库存参数:Map<Integer, Integer> inventory
public static int limitedCoinsChange(Integer[] coins, int amount, Map<Integer, Integer> inventory) {Arrays.sort(coins, Collections.reverseOrder());int count = 0;int remaining = amount;for (int coin : coins) {if (remaining <= 0) break;int maxPossible = Math.min(remaining / coin, inventory.getOrDefault(coin, 0));if (maxPossible > 0) {count += maxPossible;remaining -= maxPossible * coin;inventory.put(coin, inventory.get(coin) - maxPossible);}}return remaining == 0 ? count : -1;
}
十二、总结
12.1 关键要点回顾
- 贪心算法在规范硬币系统中高效且最优
- 降序排序是核心实现步骤
- 必须处理边界情况和非法输入
- 动态规划是更通用的替代方案
12.2 算法选择建议
- 优先验证硬币系统是否规范
- 高频交易场景使用贪心算法
- 不确定面额时使用动态规划
12.3 开发方向
- 自适应贪心策略(学习型算法)
- 量子计算在组合优化中的应用
- 区块链智能合约中的找零优化
更多资源:
https://www.kdocs.cn/l/cvk0eoGYucWA
本文发表于【纪元A梦】!
相关文章:

贪心算法应用:硬币找零问题详解
贪心算法与硬币找零问题详解 贪心算法(Greedy Algorithm)在解决优化问题时表现出简洁高效的特点,尤其适用于特定结构的组合优化问题。本文将用2万字篇幅,深入探讨贪心算法在硬币找零问题中的应用,覆盖算法原理、正确性…...

深入理解 x86 汇编中的重复前缀:REP、REPZ/REPE、REPNZ/REPNE(进阶详解版)
一、重复前缀:串操作的 “循环加速器” 如果你写过汇编代码,一定遇到过需要重复处理大量数据的场景: 复制 1000 字节的内存块比较两个长达 200 字符的字符串在缓冲区中搜索特定的特征值 手动用loop指令编写循环?代码冗长不说&a…...

计算机网络全维度解析:架构协议、关键设备、安全机制与新兴技术深度融合
计算机网络作为当今数字化社会的基石,其复杂性和应用广泛性远超想象。本文将从基础架构、协议体系、关键设备、安全机制到新兴技术,进行全方位、深层次的解析,并辅以实际应用场景和案例分析。 一、网络架构与分类的深度剖析 1.1 网络分类的立…...

Docker 在 AI 开发中的实践:GPU 支持与深度学习环境的容器化
人工智能(AI)和机器学习(ML),特别是深度学习,正以前所未有的速度发展。然而,AI 模型的开发和部署并非易事。开发者常常面临复杂的依赖管理(如 Python 版本、TensorFlow/PyTorch 版本、CUDA、cuDNN)、异构硬件(CPU 和 GPU)支持以及环境复现困难等痛点。这些挑战严重阻…...

学习NuxtLink标签
我第一次接触这个标签,我都不知道是干嘛的,哈哈哈哈,就是他长得有点像routerLink,所以我就去查了一下!哎!!!真是一样的,哈哈哈哈,至少做的事情是一样的&#…...

基于PostGIS的GeoTools执行原生SQL查询制图实践-以贵州省行政区划及地级市驻地为例
目录 前言 一、空间相关表简介 1、地市行政区划表 2、地市驻地信息表 3、空间查询检索 二、GeoTools制图实现 1、数据类型绑定 2、WKT转Geometry 3、原生SQL转SimpleFeatureCollection 4、集成调用 5、成果预览 三、总结 前言 在当今这个信息爆炸的时代,…...

MySQL字段类型完全指南:选型策略与实战应用
引言 在数据库设计中,字段类型的选择直接影响数据存储效率、查询性能和系统稳定性。本文将系统梳理MySQL支持的字段类型,结合典型应用场景与避坑指南,助你构建高性能、易维护的数据库结构。 一、字段类型全景图 MySQL字段类型主要分为以下五…...

NLP实战(5):基于LSTM的电影评论情感分析模型研究
目录 摘要 1. 引言 2. 相关工作 3. 方法 3.1 数据预处理 3.2 模型架构 3.3 训练策略 3.4 交叉验证 4. 实验与结果 4.1 数据集 4.2 实验结果 4.3训练日志 4.4 示例预测 5. 讨论 6. 结论 附录代码 展示和免费下载 摘要 本文提出了一种基于双向LSTM的深度学习模…...

DHCP应用
一、DHCP介绍 在LAN(局域网)中我们常会遇到以下的情况: 1.不知道如何配置IP地址及相关信息的员工,无法上网;2.IP地址配置冲突,无法上网;3.来访用户因不熟悉公司网络情况无法上网; 以上这些情况都是日常最…...

基于MATLAB的FTN调制和硬判决的实现
在数字通信中,FTN(Full-Transmit-Null)是一种调制技术,用于在有限带宽的信道中传输数据。FTN调制通过在符号之间插入零值,使得频谱在符号速率的整数倍处为零,从而减少频谱重叠。硬判决是一种简单的解调方式…...

涂装协作机器人:重新定义涂装工艺的智能化未来
一、涂装场景的产业变革与核心诉求 1.1 千亿级市场的技术突围战 在汽车制造领域,涂装车间被称为"工业化妆间",其工艺质量直接影响产品溢价能力。当前行业面临三重挑战: 质量维度:传统人工喷涂存在膜厚波动15μm的行业…...

c++面向对象第4天---拷贝构造函数与深复制
含有对象成员的构造函数深复制与浅复制拷贝(复制)构造函数 第一部分:含有对象成员的构造函数 以下是一个学生 类包含日期成员出生日期的代码 #include<iostream> using namespace std; class Date { public:Date(int year,int month…...

Windows版PostgreSQL 安装 vector 扩展
问题 spring-ai在集成PGVector向量存储的时候会报错如下,那么就需要安装pgsql的vector扩展。 SQL [CREATE EXTENSION IF NOT EXISTS vector]; 错误: 无法打开扩展控制文件 "C:/Program Files/PostgreSQL/9.6/share/extension/vector.control": No such …...
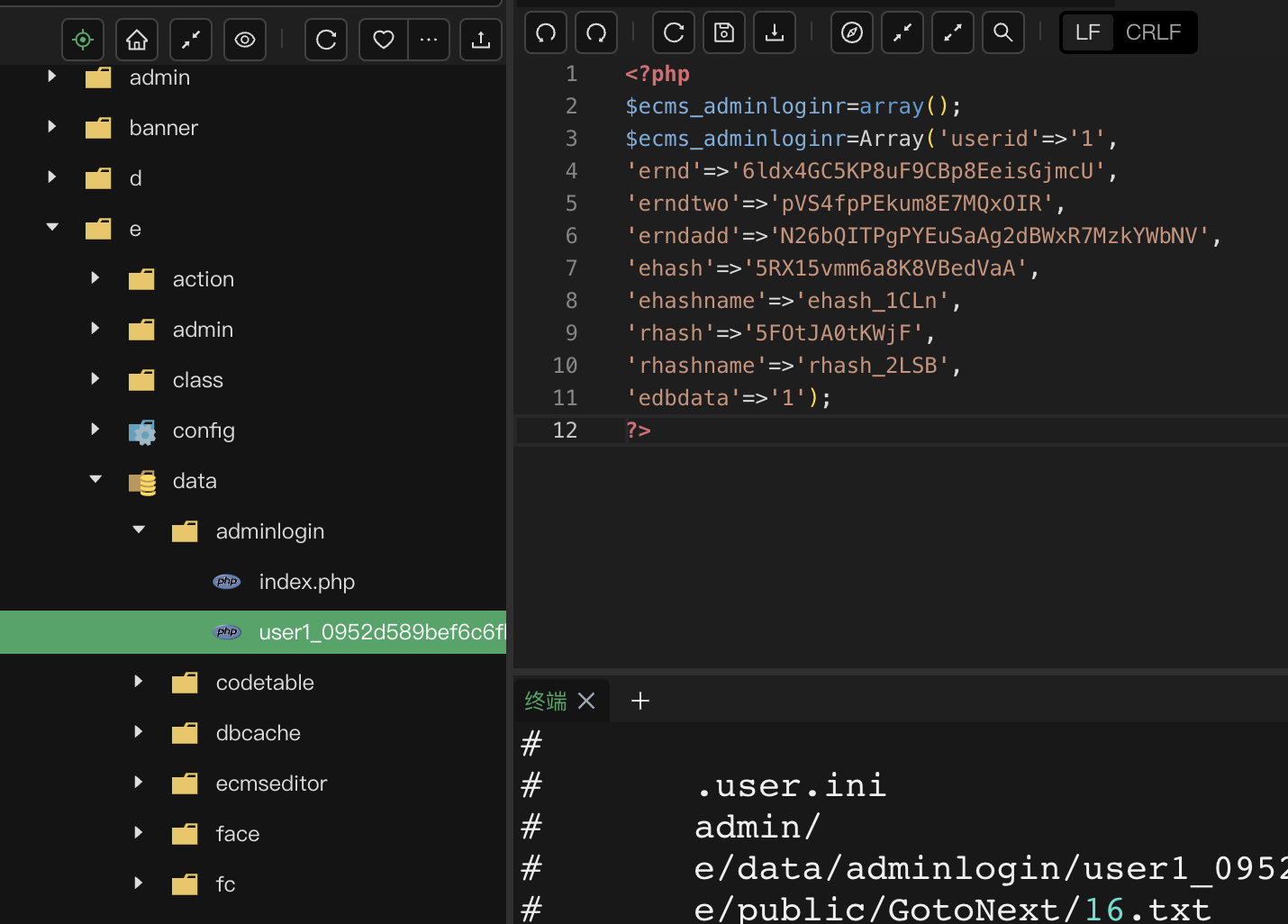
KINGCMS被入侵
现象会强制跳转到 一个异常网站,请掉截图代码. 代码中包含经过混淆处理的JavaScript,它使用了一种技术来隐藏其真实功能。代码中使用了eval函数来执行动态生成的代码,这是一种常见的技术,恶意脚本经常使用它来隐藏其真实目的。 这段脚本会检…...

完美解决在pycharm中创建Django项目安装mysqlclient报错的问题(windows下)
正常情况下,在Windows安装mysqlclient会报错: 我这里用的是anaconda虚拟环境,安装前必须激活anacoda虚拟环境, 怎么激活虚拟环境?可以参考超详细的pycharmanaconda搭建python虚拟环境_pycharm anaconda环境搭建-CSDN博…...
『React』组件副作用,useEffect讲解
在 React 开发中,有时候会听到“副作用”这个词。特别是用到 useEffect 这个 Hook 的时候,官方就明确说它是用来处理副作用的。那什么是副作用?为什么我们要专门管控它?今天就聊聊 React 中的组件副作用。 📌 什么是“…...

使用VSCode在WSL和Docker中开发
通过WSL,开发人员可以安装 Linux 发行版(例如 Ubuntu、OpenSUSE、Kali、Debian、Arch Linux 等),并直接在 Windows 上使用 Linux 应用程序、实用程序和 Bash 命令行工具,不用进行任何修改,也无需使用传统虚…...

ZooKeeper 命令操作
文章目录 Zookeeper 数据模型Zookeeper 服务端常用命令Zookeeper 客户端常用命令 Zookeeper 数据模型 ZooKeeper 是一个树形目录服务,其数据模型和Unix的文件系统目录树很类似,拥有一个层次化结构。这里面的每一个节点都被称为: ZNode,每个节…...

解决 Ubuntu 20.04 虚拟机中 catkin_make 编译卡死问题
完整解决步骤 1. 禁用当前交换文件 sudo swapoff /swapfile 2. 删除旧的交换文件 sudo rm /swapfile 3. 使用更可靠的创建方法 # 使用 dd 命令创建交换文件(更兼容但较慢) sudo dd if/dev/zero of/swapfile bs1M count4096# 或者使用 truncate 命令…...

【HTML-15】HTML表单:构建交互式网页的基石
表单是HTML中最强大的功能之一,它允许网页收集用户输入并与服务器进行交互。无论是简单的搜索框、登录页面,还是复杂的多步骤调查问卷,表单都是实现这些功能的核心元素。本文将深入探讨HTML表单的各个方面,帮助您构建高效、用户友…...

一些较好的学习方法
1、网上有一些非常经典的电路,而且有很多视频博主做了详细的讲解。 2、有一部分拆解的UP主,拆解后会还原该器件的原理图,并一步步做讲解。 3、有两本书,数电、模电,这两本书中的内容很多都值得学习。 5、某宝上卖的…...
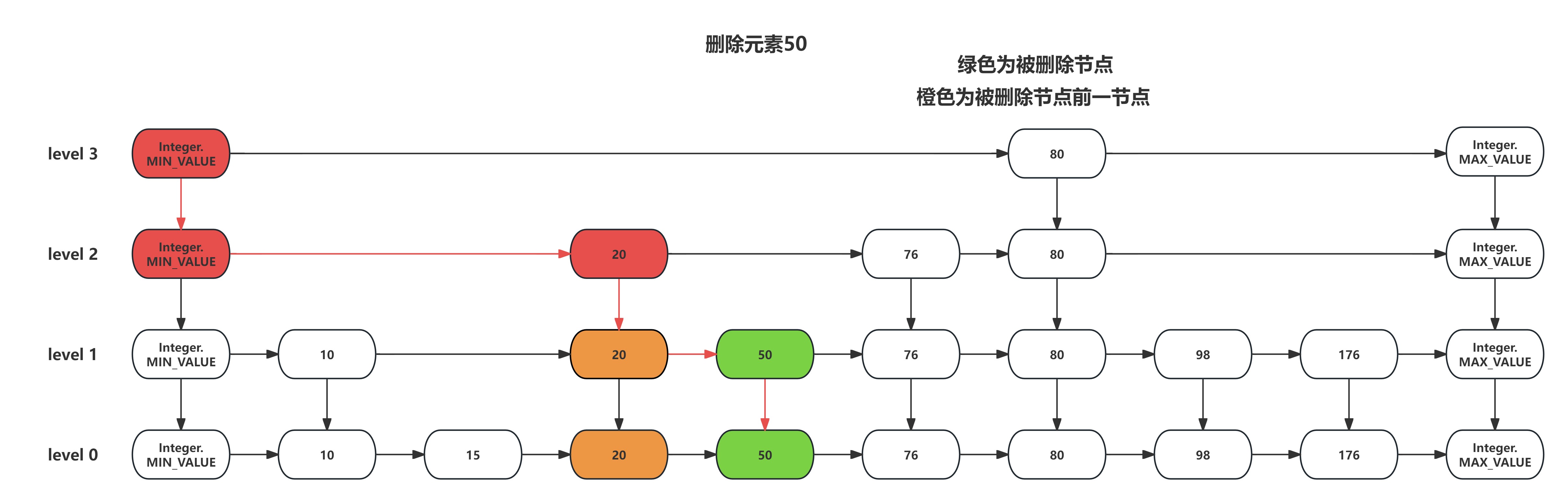
Redis底层数据结构之深入理解跳表(1)
在上一篇文章中我们详细的介绍了一下Redis中跳表的结构以及为什么Redis要引入跳表而不是平衡树或红黑树。这篇文章我们就来详细梳理一下跳表的增加、搜索和删除步骤。 SkipList的初始化 跳表初始化时,将每一层链表的头尾节点创建出来并使用集合将头尾节点进行存储&…...
的实战教程)
鸿蒙【HarmonyOS 5】 (React Native)的实战教程
一、环境配置 安装鸿蒙专属模板 bashCopy Code npx react-native0.72.5 init HarmonyApp --template react-native-template-harmony:ml-citation{ref"4,6" data"citationList"} 配置 ArkTS 模块路径 在 entry/src/main/ets 目录下创建原生模块&…...

PCB设计教程【入门篇】——电路分析基础-元件数据手册
前言 本教程基于B站Expert电子实验室的PCB设计教学的整理,为个人学习记录,旨在帮助PCB设计新手入门。所有内容仅作学习交流使用,无任何商业目的。若涉及侵权,请随时联系,将会立即处理 目录 前言 一、数据手册的重要…...

20250529-C#知识:继承、密封类、密封方法、重写
C#知识:继承、密封类、密封方法、重写 继承是面向对象的三大特性之一,通过继承能够减少重复代码的编写,有助于提升开发效率。 1、继承 C#不同于C,只支持单继承当子类出现与父类同名的成员时,父类成员被隐藏࿰…...

从0到1,带你走进Flink的世界
目录 一、Flink 是什么? 二、Flink 能做什么? 三、Flink 架构全景概览 3.1 分层架构剖析 3.2 核心组件解析 四、Flink 的核心概念 4.1 数据流与数据集 4.2 转换操作 4.3 窗口 4.4 时间语义 4.5 状态与检查点 五、Flink 安装与快速上手 5.1 …...

springboot @value
#springboot value value 可以读取 yaml 中 的数据...

Dify-5:Web 前端架构
本文档提供了 Dify Web 前端架构的技术概述,包括核心组件、结构和关键技术。它解释了前端如何组织、组件如何通信以及国际化功能如何实现。 技术栈 Dify 的 Web 前端基于现代 JavaScript 技术栈构建: 框架:Next.js(基于 React …...

深度学习赋能图像识别:技术、应用与展望
论文: 一、引言 1.1 研究背景与意义 在当今数字化时代,图像作为信息的重要载体,广泛存在于各个领域。图像识别技术旨在让计算机理解和识别图像内容,将图像中的对象、场景、行为等信息转化为计算机能够处理的符号或数据 &am…...

八N皇后问题
1 问题的提出 在8X8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法 我们的任务就是用MATLAB进行求解 2 数学模型的构建 首先我们分析题目就是 任意两个皇后都不能处于…...
