贪心算法应用:在线租赁问题详解

贪心算法应用:在线租赁问题详解
贪心算法是一种在每一步选择中都采取当前状态下最优的选择,从而希望导致结果是全局最优的算法策略。在线租赁问题(Greedy Algorithm for Online Rentals)是一个经典的贪心算法应用场景,下面我将从多个维度全面详细地讲解这个问题及其Java实现。
一、问题定义与理解
1.1 问题描述
在线租赁问题可以描述为:假设你经营一家设备租赁公司,有若干台相同的设备可供出租。客户会在一段时间内陆续提出租赁请求,每个请求包含开始时间和结束时间。你的目标是接受尽可能多的租赁请求,使得这些请求在时间上不冲突。
1.2 问题形式化
给定:
- 一组租赁请求R = {r₁, r₂, …, rₙ}
- 每个请求rᵢ = (sᵢ, fᵢ),其中sᵢ是开始时间,fᵢ是结束时间
目标:
- 选择一个最大子集S ⊆ R,使得对于任何两个请求rᵢ, rⱼ ∈ S,区间[sᵢ, fᵢ)和[sⱼ, fⱼ)不重叠
1.3 实际应用场景
- 会议室安排
- 课程表安排
- 电影院放映厅排片
- 计算资源分配
- 医院手术室安排
二、贪心算法策略分析
2.1 可能的贪心策略
对于这类区间调度问题,常见的贪心策略有:
- 最早开始时间优先:选择开始时间最早的请求
- 最短持续时间优先:选择持续时间(fᵢ - sᵢ)最短的请求
- 最少冲突优先:选择与其他请求冲突最少的请求
- 最早结束时间优先:选择结束时间最早的请求
2.2 策略正确性分析
经过分析,最早结束时间优先的策略可以产生最优解:
- 最早开始时间优先:反例 - 一个很早开始但很长的请求可能阻止多个短请求
- 最短持续时间优先:反例 - 可能存在多个短请求都冲突于一个长请求
- 最少冲突优先:计算复杂且不一定最优
- 最早结束时间优先:总是留下最多剩余时间安排其他请求
2.3 贪心选择性质证明
要证明最早结束时间优先策略的正确性:
- 设O是最优解,G是我们的贪心解
- 设r₁是G中第一个选择的请求,也是最早结束的请求
- 如果O的第一个请求不是r₁,我们可以用r₁替换O的第一个请求,仍然保持最优
- 通过归纳法,可以证明G与O同样最优
三、算法设计与实现
3.1 算法步骤
- 将所有租赁请求按照结束时间升序排序
- 初始化选择的请求集合S为空,当前结束时间prev_f为0
- 对于每个请求rᵢ按排序后的顺序:
- 如果sᵢ ≥ prev_f(不冲突):
- 将rᵢ加入S
- 更新prev_f = fᵢ
- 如果sᵢ ≥ prev_f(不冲突):
- 返回S作为最终选择
3.2 Java实现
import java.util.Arrays;
import java.util.Comparator;
import java.util.ArrayList;
import java.util.List;class RentalRequest {int id;int start;int end;public RentalRequest(int id, int start, int end) {this.id = id;this.start = start;this.end = end;}@Overridepublic String toString() {return "Request " + id + ": [" + start + ", " + end + "]";}
}public class OnlineRentalScheduler {// 贪心算法解决在线租赁问题public static List<RentalRequest> scheduleRentals(RentalRequest[] requests) {// 1. 按照结束时间排序Arrays.sort(requests, new Comparator<RentalRequest>() {@Overridepublic int compare(RentalRequest r1, RentalRequest r2) {return r1.end - r2.end;}});List<RentalRequest> selected = new ArrayList<>();int lastEndTime = 0;// 2. 选择不冲突的请求for (RentalRequest req : requests) {if (req.start >= lastEndTime) {selected.add(req);lastEndTime = req.end;}}return selected;}public static void main(String[] args) {// 示例请求RentalRequest[] requests = {new RentalRequest(1, 1, 4),new RentalRequest(2, 3, 5),new RentalRequest(3, 0, 6),new RentalRequest(4, 5, 7),new RentalRequest(5, 3, 8),new RentalRequest(6, 5, 9),new RentalRequest(7, 6, 10),new RentalRequest(8, 8, 11),new RentalRequest(9, 8, 12),new RentalRequest(10, 2, 13),new RentalRequest(11, 12, 14)};List<RentalRequest> scheduled = scheduleRentals(requests);System.out.println("Selected Rental Requests:");for (RentalRequest req : scheduled) {System.out.println(req);}System.out.println("Total scheduled: " + scheduled.size());}
}
3.3 代码解析
- RentalRequest类:表示一个租赁请求,包含ID、开始时间和结束时间
- scheduleRentals方法:
- 使用Comparator按结束时间排序
- 遍历排序后的请求,选择不冲突的请求
- main方法:提供测试用例并输出结果
四、算法复杂度分析
4.1 时间复杂度
- 排序阶段:O(n log n),使用Arrays.sort()的快速排序或归并排序
- 选择阶段:O(n),只需一次线性扫描
- 总时间复杂度:O(n log n) 主导
4.2 空间复杂度
- 排序:O(log n) 的栈空间(Java排序算法的空间复杂度)
- 存储结果:O(k),k是最终选择的请求数(最坏情况O(n))
- 总空间复杂度:O(n)
五、算法正确性验证
5.1 示例验证
对于给定的示例请求:
Request 1: [1, 4]
Request 2: [3, 5]
Request 3: [0, 6]
Request 4: [5, 7]
Request 5: [3, 8]
Request 6: [5, 9]
Request 7: [6, 10]
Request 8: [8, 11]
Request 9: [8, 12]
Request 10: [2, 13]
Request 11: [12, 14]
排序后:
Request 3: [0, 6]
Request 1: [1, 4]
Request 2: [3, 5]
Request 4: [5, 7]
Request 5: [3, 8]
Request 6: [5, 9]
Request 7: [6, 10]
Request 8: [8, 11]
Request 9: [8, 12]
Request 10: [2, 13]
Request 11: [12, 14]
贪心选择过程:
- 选择Request 1: [1,4], lastEndTime=4
- 跳过Request 2: [3,5] (3<4)
- 选择Request 4: [5,7], lastEndTime=7
- 跳过Request 5-7
- 选择Request 8: [8,11], lastEndTime=11
- 选择Request 11: [12,14], lastEndTime=14
最终选择4个请求,这是最大可能的不冲突集合。
5.2 边界情况测试
- 无请求:返回空列表
- 所有请求冲突:只选择第一个结束最早的
- 无冲突请求:选择所有请求
- 相同结束时间:按排序顺序选择第一个不冲突的
六、算法优化与变种
6.1 多资源情况
当有k个相同的租赁设备时,问题变为k-区间调度问题:
public static List<List<RentalRequest>> scheduleRentalsWithKResources(RentalRequest[] requests, int k) {Arrays.sort(requests, Comparator.comparingInt(r -> r.end));List<List<RentalRequest>> resources = new ArrayList<>();for (int i = 0; i < k; i++) {resources.add(new ArrayList<>());}int[] lastEndTimes = new int[k];for (RentalRequest req : requests) {for (int i = 0; i < k; i++) {if (req.start >= lastEndTimes[i]) {resources.get(i).add(req);lastEndTimes[i] = req.end;break;}}}return resources;
}
6.2 加权区间调度
如果每个请求有不同的权重(利润),贪心算法不再适用,需要使用动态规划:
public static int maxWeightSchedule(RentalRequest[] requests) {Arrays.sort(requests, Comparator.comparingInt(r -> r.end));int n = requests.length;int[] dp = new int[n + 1];for (int i = 1; i <= n; i++) {int profit = requests[i-1].end - requests[i-1].start; // 假设权重为持续时间int prevCompatible = findLastNonConflict(requests, i);dp[i] = Math.max(dp[i-1], (prevCompatible == -1 ? 0 : dp[prevCompatible]) + profit);}return dp[n];
}private static int findLastNonConflict(RentalRequest[] requests, int index) {int low = 0, high = index - 1;while (low <= high) {int mid = (low + high) / 2;if (requests[mid].end <= requests[index-1].start) {if (requests[mid+1].end <= requests[index-1].start) {low = mid + 1;} else {return mid + 1;}} else {high = mid - 1;}}return -1;
}
6.3 在线算法版本
当请求实时到达无法预先排序时,可以使用在线算法:
public class OnlineRentalScheduler {private int lastEndTime = 0;public boolean processRequest(RentalRequest request) {if (request.start >= lastEndTime) {lastEndTime = request.end;return true;}return false;}
}
七、实际应用中的考虑
7.1 请求预处理
在实际应用中,可能需要:
- 验证时间有效性(开始<结束)
- 处理时间格式转换
- 过滤无效请求
7.2 多维度约束
可能需要考虑:
- 设备类型匹配
- 客户优先级
- 价格因素
- 地理位置限制
7.3 性能优化
对于大规模数据:
- 使用并行排序
- 考虑分治策略
- 使用更高效的数据结构
八、与其他算法对比
8.1 与动态规划对比
| 特性 | 贪心算法 | 动态规划 |
|---|---|---|
| 时间复杂度 | O(n log n) | O(n²)或O(n log n) |
| 适用问题 | 具有贪心选择性质的问题 | 具有最优子结构的问题 |
| 加权支持 | 不支持 | 支持 |
| 实现复杂度 | 简单 | 较复杂 |
8.2 与回溯算法对比
贪心算法:
- 效率高
- 不能保证所有情况的最优解
- 无法回溯撤销选择
回溯算法:
- 可以找到所有解
- 时间复杂度高(O(2^n))
- 适合小规模问题
九、常见问题与解决方案
9.1 如何处理时间重叠但资源充足的情况?
解决方案:修改冲突检测逻辑,跟踪每个资源的最后使用时间。
9.2 如何扩展算法以支持不同类型的设备?
解决方案:为每种设备类型维护单独的调度列表。
9.3 如何实现实时更新的调度?
解决方案:使用合适的数据结构(如TreeSet)来高效插入和查询。
十、总结
贪心算法在在线租赁问题中提供了高效且简单的解决方案。通过选择最早结束的请求,算法能够最大化可接受的请求数量。Java实现展示了如何通过排序和线性扫描来解决这个问题。虽然贪心算法不能解决所有变种问题(如加权情况),但对于基本的区间调度问题,它是最优的选择。
关键要点:
- 贪心算法的核心是做出局部最优选择
- 正确性依赖于问题具有贪心选择性质
- 排序是此类问题的常见预处理步骤
- Java的Comparator接口提供了灵活的排序方式
- 算法可以扩展以适应更复杂的实际需求
更多资源:
https://www.kdocs.cn/l/cvk0eoGYucWA
本文发表于【纪元A梦】!
相关文章:

贪心算法应用:在线租赁问题详解
贪心算法应用:在线租赁问题详解 贪心算法是一种在每一步选择中都采取当前状态下最优的选择,从而希望导致结果是全局最优的算法策略。在线租赁问题(Greedy Algorithm for Online Rentals)是一个经典的贪心算法应用场景,下面我将从多个维度全面…...
用法简介)
torch.zeros()用法简介
torch.zeros()是PyTorch中用于创建全零张量的核心函数,其功能和使用方法如下: 1. 基本语法 torch.zeros(*size, outNone, dtypeNone, layouttorch.strided, deviceNone, requires_gradFalse)参数说明: *size:定义张量形状的…...

Prj10--8088单板机C语言8259测试(1)
1.原理图 2.Deepseek示例代码 #include <dos.h> #include <conio.h> #include <stdio.h>#define PIC1_CMD 0x400 // 命令端口 (A00) #define PIC1_DATA 0x401 // 数据端口 (A01)volatile int int_count 0; // 中断计数器 void interrupt (*old_isr)(…...

3步在小米13手机跑DeepSeek R1
大家好!我是羊仔,专注AI工具、智能体、编程。 一、从性能旗舰到AI主机 春节大扫除时,翻出尘封的小米13,这台曾以骁龙8 Gen2著称的性能小钢炮,如今正在执行更科幻的使命——本地运行DeepSeek R1。 想起两年前用它连续肝…...
)
数智管理学(十六)
二、分布式网络型结构的特点 分布式网络型结构是一种去中心化、扁平化和协作性的组织模式,与传统金字塔型结构形成鲜明对比。它通过赋予团队和个体更大的自主权,提升组织的灵活性和响应能力。 (一)节点化组织 1.模块化团队构成…...

注销微软账户
因为我的微软开发者账户丢失 Office E5 权限,因此需要注销。 若你需要注销微软账号,请点击下方超链接。 点击此处 注销之后仅剩一个正常的账户使用咯!!...

Ubuntu 服务器软件更新,以及常用软件安装 —— 一步一步配置 Ubuntu Server 的 NodeJS 服务器详细实录 3
前言 前面,我们已经 安装好了 Ubuntu 服务器系统,并且 配置好了 ssh 免密登录服务器 ,现在,我们要来进一步的设置服务器。 那么,本文,就是进行服务器的系统更新,以及常用软件的安装 调整 Ubu…...

Mysql常用知识3:Kafka和数据库优化
文章目录 一、分布式消息系统(Kafka相关问题5-10)5. Kafka如何保证消息不丢失?6. 项目中Kafka具体怎么使用的?7. 消息异常未发送成功怎么解决?8. 重试具体怎么做的,循环吗?9. 重试多次失败怎么办…...

Milvus单机模式安装和试用
1.安装ollama的package包; # install package pip install -U langchain-ollama2.我们直接使用ChatOllama实例化模型,并通过invoke进行调用; from langchain_ollama import ChatOllamallm ChatOllama(model"deepseek-r1") messa…...
飞牛NAS+Docker技术搭建个人博客站:公网远程部署实战指南
文章目录 前言1. Docker下载源设置2. Docker下载WordPress3. Docker部署Mysql数据库4. WordPress 参数设置5. 飞牛云安装Cpolar工具6. 固定Cpolar公网地址7. 修改WordPress配置文件8. 公网域名访问WordPress总结 前言 在数字化浪潮中,传统网站搭建方式正面临前所未…...
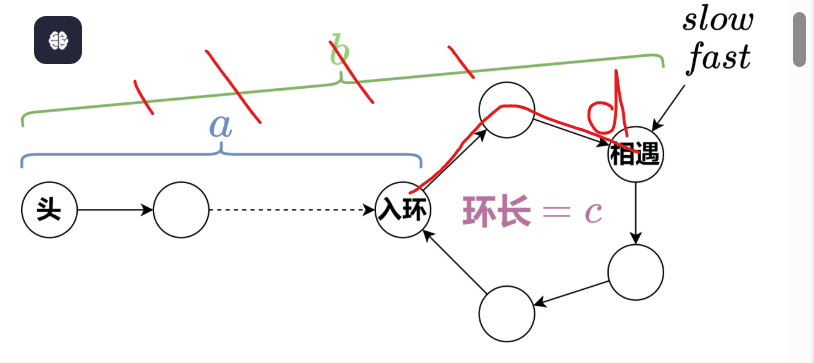
刷leetcode hot100返航必胜版--链表6/3
链表初始知识 链表种类:单链表,双链表,循环链表 链表初始化 struct ListNode{ int val; ListNode* next; ListNode(int x): val(x),next(nullptr) {} }; //初始化 ListNode* head new ListNode(5); 删除节点、添加…...

C# 序列化技术全面解析:原理、实现与应用场景
在软件开发中,数据持久化和网络通信是两个至关重要的环节。想象一下,当我们需要将一个复杂的对象保存到文件中,或者通过网络发送到另一台计算机时,如何有效地表示这个对象?这就是序列化技术要解决的问题。序列化&#…...

isp调试 blend模式指什么
isp调试 blend模式指什么 答案摘自豆包: 在图像信号处理(ISP,Image Signal Processor)调试中,Blend 模式(混合模式) 是指将不同处理阶段的图像数据或不同来源的图像信息按照特定规则进行叠加或…...
electron定时任务,打印内存占用情况
// 监听更新 function winUpdate(){// 每次执行完后重新设置定时器try {// 获取当前时间并格式化为易读的字符串const now new Date();const timeString now.toLocaleString();console.log(当前时间: ${timeString});// 记录内存使用情况(可选)const m…...

Gitee Wiki:以知识管理赋能 DevSecOps,推动关键领域软件自主演进
关键领域软件研发中的知识管理困境 传统文档管理模式问题显著 关键领域软件研发领域,传统文档管理模式问题显著:文档存储无系统,查找困难,降低效率;更新不及时,与实际脱节,误导开发࿱…...

学习STC51单片机24(芯片为STC89C52RCRC)
每日一言 把 “我不行” 换成 “我试试”,你会发现一片新的天地。 那关于优化 白盒测试 我们之前不是通过这个接线方式可以看到返回到信息嘛因为安信可的特性就是返回Esp8266的反馈,可以看到代码死在哪里了,导致连接不上,因为我们…...

LabVIEW基于 DataSocket从 OPC 服务器读取数据
LabVIEW 中基于 DataSocket 函数从 OPC 服务器读取数据的功能,为工业自动化等场景下的数据交互提供了解决方案。通过特定函数实现 URL 指定、连接建立与管理、数据读取,相比传统 Socket 通信和 RESTful API ,在 OPC 服务器数据交互场景有适配…...

阿里云无影云桌面深度测评
阿里云无影桌面深度测评:解锁云端工作“新范式”的“未来之钥”! 在数字化浪潮席卷全球的2025年,远程办公与混合办公已不再是权宜之计,而是职场不可逆转的新常态。然而,如何确保员工无论身在何处,都能拥有…...

【208】VS2022 C++ 32位整数和unsigned char数组之间互相转换
一、场景 在实际应用中,特别是在数据传输的时候,需要读取unsigned char数组,再转换成 32 位整数;或者把 32 位整数转换成 unsigned char数组进行写入。比如对接西门子PLC的 snap7 就是这样。32 位整数分成有符号的无符号的&#…...

数据库技术
InnoDB是什么?MySQL 和 InnoDB的关系是什么? InnoDB是MySQL数据库系统中最重要且默认的存储引擎。MySQL采用插件式存储引擎架构,作为数据库管理系统本身不直接处理数据存储,而是通过存储引擎接口与InnoDB等引擎交互。InnoDB作为M…...

深入浅出:Oracle 数据库 SQL 执行计划查看详解(1)——基础概念与查看方式
背景 在当今的软件开发领域,尽管主流开发模式往往倾向于采用单表模式,力图尽可能地减少表之间的连接操作,以期达到提高数据处理效率、简化应用逻辑等目的。然而,对于那些已经上线运行多年的运维老系统而言,它们内部往…...

前端HTML contenteditable 属性使用指南
什么是 contenteditable? HTML5 提供的全局属性,使元素内容可编辑类似于简易富文本编辑器兼容性 支持所有现代浏览器(Chrome、Firefox、Safari、Edge) 移动端(iOS/Android)部分键盘行为需测试 &l…...

自动化采集脚本与隧道IP防封设计
最近群里讨论问如何编写一个自动化采集脚本,要求使用隧道IP(代理IP池)来防止IP被封。这样的脚本通常用于爬虫或数据采集任务,其中目标网站可能会因为频繁的请求而封禁IP。对于这些我还是有些经验的。 核心思路: 1、使…...

【设计模式-4.7】行为型——备忘录模式
说明:本文介绍行为型设计模式之一的备忘录模式 定义 备忘录模式(Memento Pattern)又叫作快照模式(Snapshot Pattern)或令牌模式(Token Pattern)指在不破坏封装的前提下,捕获一个对…...

docker离线镜像下载
背景介绍 在某些网络受限的环境中,直接从Docker Hub或其他在线仓库拉取镜像可能会遇到困难。为了在这种情况下也能顺利使用Docker镜像,我们可以提前下载好所需的镜像,并通过离线方式分发和使用。 当前镜像有:python-3.8-slim.ta…...

Vert.x学习笔记-Verticle原理解析
Vert.x学习笔记 一、设计理念:事件驱动的组件化模型二、生命周期管理三、部署方式与策略四、通信机制:事件总线(Event Bus)五、底层实现原理六、典型应用场景七、Verticle与EventLoop的关系1、核心关系:一对一绑定与线…...

Cobra CLI 工具使用指南:构建 Go 语言命令行应用的完整教程
Cobra CLI 工具使用指南:构建 Go 语言命令行应用的完整教程 在 Go 语言开发中,构建功能强大的命令行界面(CLI)应用是常见需求。Cobra 作为 Go 生态中最受欢迎的 CLI 库,凭借其灵活的设计和丰富的功能,成为…...

jQuery和CSS3卡片列表布局特效
这是一款jQuery和CSS3卡片列表布局特效。该卡片布局使用owl.carousel.js来制作轮播效果,使用简单的css代码来制作卡片布局,整体效果时尚大方。 预览 下载 使用方法 在页面最后引入jquery和owl.carousel.js相关文件。 <link rel"stylesheet&qu…...

不连网也能跑大模型?
一、这是个什么 App? 你有没有想过,不用连网,你的手机也能像 ChatGPT 那样生成文字、识别图片、甚至回答复杂问题?Google 最近悄悄发布了一个实验性 Android 应用——AI Edge Gallery,就是为此而生的。 这个应用不在…...

强化学习鱼书(10)——更多深度强化学习的算法
:是否使用环境模型(状态迁移函数P(s’|s,a)和奖 励函数r(s,a,V))。不使用环境模型的方法叫作无模型(model-free)的方法,使用环境模型的方法叫作有模型(model-based&#…...
