复变函数中的对数函数及其MATLAB演示
复变函数中的对数函数及其MATLAB演示
引言
在实变函数中,对数函数 ln x \ln x lnx定义在正实数集上,是一个相对简单的概念。然而,当我们进入复变函数领域时,对数函数展现出更加丰富和复杂的性质。本文将介绍复变函数中对数函数的基本概念、性质,并通过MATLAB进行可视化演示。
复对数函数的定义
复对数函数是实对数函数的推广。对于非零复数 z z z,其对数定义为:
ln z = ln ∣ z ∣ + i ( Arg ( z ) + 2 π k ) , k ∈ Z \ln z = \ln|z| + i(\operatorname{Arg}(z) + 2\pi k),\quad k \in \mathbb{Z} lnz=ln∣z∣+i(Arg(z)+2πk),k∈Z
这里:
- ∣ z ∣ |z| ∣z∣是 z z z的模
- Arg ( z ) \operatorname{Arg}(z) Arg(z)是 z z z的主辐角(通常取 ( − π , π ] (-\pi, \pi] (−π,π])
- k k k为任意整数,表明复对数是一个多值函数
主值(当 k = 0 k=0 k=0时)记为:
Ln z = ln ∣ z ∣ + i Arg ( z ) \operatorname{Ln} z = \ln|z| + i\operatorname{Arg}(z) Lnz=ln∣z∣+iArg(z)
复对数的性质
- 多值性:复对数函数有无穷多个值,各值相差 2 π i 2\pi i 2πi的整数倍
MATLAB演示
计算复对数:
MATLAB中使用log函数计算复对数的主值:
z = 1 + 1i;
ln_z = log(z);
disp(['主值: ', num2str(ln_z)]);
disp(['实部(ln|z|): ', num2str(real(ln_z))]);
disp(['虚部(Arg(z)): ', num2str(imag(ln_z))]);
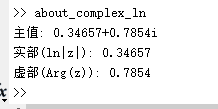
运行结果:
结论
Matlab中log函数可以直接计算复数的主值
相关文章:

复变函数中的对数函数及其MATLAB演示
复变函数中的对数函数及其MATLAB演示 引言 在实变函数中,对数函数 ln x \ln x lnx定义在正实数集上,是一个相对简单的概念。然而,当我们进入复变函数领域时,对数函数展现出更加丰富和复杂的性质。本文将介绍复变函数中对数函…...

【Linux】Linux程序地址基础
参考博客:https://blog.csdn.net/sjsjnsjnn/article/details/125533127 一、地址空间的阐述 1.1 程序地址空间 下面的图片展示了程序地址空间的组成结构 我们通过代码来验证一下 int g_unval; int g_val 100;int main(int argc, char *argv[]);void test1() {i…...

React 项目初始化与搭建指南
React 项目初始化有多种方式,可以选择已有的脚手架工具快速创建项目,也可以自定义项目结构并使用构建工具实现项目的构建打包流程。 1. 脚手架方案 1.1. Vite 通过 Vite 创建 React 项目非常简单,只需一行命令即可完成。Vite 的工程初始化…...

将图形可视化工具的 Python 脚本打包为 Windows 应用程序
前文我们已经写了一个基于python的tkinter库和matplotlib库的图形可视化工具。 基于Python的tkinter库的图形可视化工具(15种图形的完整代码):基于Python的tkinter库的图形可视化工具(15种图形的完整代码)-CSDN博客 在前文基础上&…...

AWS DocumentDB vs MongoDB:数据库的技术抉择
随着非关系型数据库在现代应用中的广泛应用,文档型数据库因其灵活的结构与出色的扩展性,逐渐成为企业开发与架构设计中的核心选择。在众多文档数据库中,MongoDB 凭借其成熟生态与社区支持占据主导地位;与此同时,AWS 提…...

无人机军用与民用技术对比分析
一、材料区别 军用无人机: 1. 高强度特种材料: 大量使用钛合金、碳纤维复合材料,兼顾轻量化与高强度,提升抗冲击性和隐身性能。 关键部件依赖进口材料。 2. 隐身涂层: 采用雷达吸波材料和低红外特征涂料…...
刷leetcode hot100--矩阵6/1
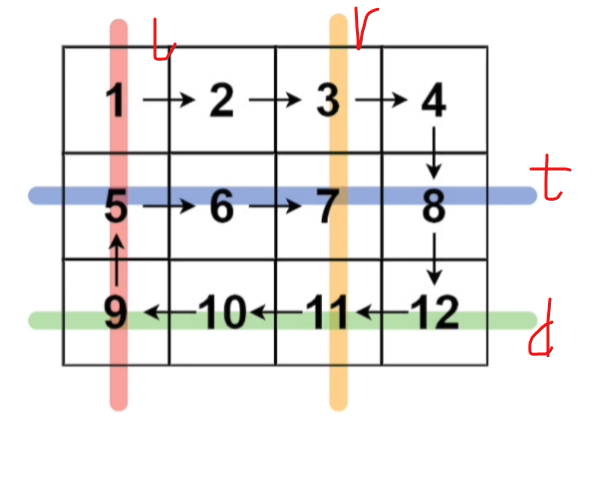
1.螺旋矩阵【很久】6/1【感觉就是思路的搬运工,没完全理解】 54. 螺旋矩阵 - 力扣(LeetCode) 原来想 但是如果是奇数矩阵,遍历不到中间 解决思路: 用left,right,top,down标记/限定每次遍历的元素,每次从…...
的功能。Qt 提供了此方法来处理过长的文本显示问题,例如在界面中限制文本长度并添加省略号(...))
Qt 中实现文本截断(ellipsis)的功能。Qt 提供了此方法来处理过长的文本显示问题,例如在界面中限制文本长度并添加省略号(...)
QElidedText 并不是 Qt 中的标准类名或功能名称,但根据你的描述,你可能是指 QFontMetrics::elidedText() 方法。这是一个用于在 Qt 中实现文本截断(ellipsis)的功能。Qt 提供了此方法来处理过长的文本显示问题,例如在界…...
)
Cisco IOS XE WLC 任意文件上传漏洞复现(CVE-2025-20188)
免责申明: 本文所描述的漏洞及其复现步骤仅供网络安全研究与教育目的使用。任何人不得将本文提供的信息用于非法目的或未经授权的系统测试。作者不对任何由于使用本文信息而导致的直接或间接损害承担责任。如涉及侵权,请及时与我们联系,我们将尽快处理并删除相关内容。 前…...

基于ResNet残差网络优化梯度下降算法实现图像分类
文章目录 题 目: 基于ResNet残差网络优化梯度下降算法实现图像分类基于ResNet残差神经网络优化梯度下降算法实现海贼王图像分类引言1.ResNet残差神经网络介绍1.1 ResNet残差神经网络的研究现状1.2 ResNet残差神经网络的原理1.3 ResNet残差神经网络的实现步骤1.3.1导入必要的库…...

群晖NAS套件历史版本资源
有时候需要下载历史的群晖套件,可以通过以下地址前往 Synology Archive Download Site - Index of /download 该页面汇集了各类群晖应用程序的过往版本,方便用户根据需要选择特定版本的软件进行下载安装。这种方式适用于需要旧版软件兼容性或进行版本回…...

Docker轻松搭建Neo4j+APOC环境
Docker轻松搭建Neo4jAPOC环境 一、简介二、Docker部署neo4j三、Docker安装APOC插件四、删除数据库/切换数据库 一、简介 Neo4j 是一款高性能的 原生图数据库,采用 属性图模型 存储数据,支持 Cypher查询语言,适用于复杂关系数据的存储和分析。…...

定制开发开源AI智能名片S2B2C商城小程序在无界零售中的应用与行业智能升级示范研究
摘要:本文聚焦无界零售背景下京东从零售产品提供者向零售基础设施提供者的转变,探讨定制开发开源AI智能名片S2B2C商城小程序在这一转变中的应用。通过分析该小程序在商业运营成本降低、效率提升、用户体验优化等方面的作用,以及其与京东AI和冯…...

CppCon 2015 学习:CLANG/C2 for Windows
Visual Studio 2015 引入了基于 CLANG/LLVM 的新代码生成器,及其背景和意义。简单理解如下: 理解要点: VS2015 中引入了全新的代码生成技术,性能和质量都很棒。这套新技术基于 Clang,微软展示了相关新工具。Clang 和…...

Spring中@Primary注解的作用与使用
在 Spring 框架中,Primary 注解用于解决依赖注入时的歧义性(Ambiguity)问题。当 Spring 容器中存在多个相同类型的 Bean 时,通过 Primary 标记其中一个 Bean 作为默认的首选注入对象。 核心作用: 解决多个同类型 Bean …...

Spring Boot + Elasticsearch + HBase 构建海量数据搜索系统
Spring Boot Elasticsearch HBase 构建海量数据搜索系统 📖 目录 1. 系统需求分析2. 系统架构设计3. Elasticsearch 与 HBase 集成方案4. Spring Boot 项目实现5. 大规模搜索系统最佳实践 项目概述 本文档提供了基于 Spring Boot、Elasticsearch 和 HBase 构建…...
)
[zynq] Zynq Linux 环境下 AXI BRAM 控制器驱动方法详解(代码示例)
Zynq Linux 环境下 AXI BRAM 控制器驱动方法详解 文章目录 Zynq Linux 环境下 AXI BRAM 控制器驱动方法详解1. UIO (Userspace I/O) 驱动方法完整示例代码 2. /dev/mem 直接内存映射方法完整示例代码 3. 自定义字符设备驱动方法完整示例代码 4. 方法对比总结5. 实战建议 在 Zyn…...

【大模型:知识图谱】--5.neo4j数据库管理(cypher语法2)
目录 1.节点语法 1.1.CREATE--创建节点 1.2.MATCH--查询节点 1.3.RETURN--返回节点 1.4.WHERE--过滤节点 2.关系语法 2.1.创建关系 2.2.查询关系 3.删除语法 3.1.DELETE 删除 3.2.REMOVE 删除 4.功能补充 4.1.SET (添加属性) 4.2.NULL 值 …...

六、数据库的安全性
六、数据库的安全性 数据库的安全问题 数据库中的数据是可以共享的数据共享必然带来数据库的安全性问题 数据库系统中的数据共享不能是无条件的共享数据库中数据的共享是在 DBMS 统一的严格控制之下的共享,即:只允许有合法使用权限的用户访其被授权的数…...

贪心算法应用:装箱问题(BFD算法)详解
贪心算法应用:装箱问题(BFD算法)详解 1. 装箱问题与BFD算法概述 1.1 装箱问题定义 装箱问题(Bin Packing Problem)是组合优化中的经典问题,其定义为: 给定n个物品,每个物品有大小wᵢ (0 < wᵢ ≤ C)无限数量的箱子…...

C#学习第27天:时间和日期的处理
时间和日期的核心概念 1. UTC 和 本地时间 UTC(Coordinated Universal Time): 是一种不受时区影响的世界标准时间。在网络通信和全球协作中,用于统一时间度量 本地时间(Local Time): 是根据所…...

编程技能:格式化打印05,格式控制符
专栏导航 本节文章分别属于《Win32 学习笔记》和《MFC 学习笔记》两个专栏,故划分为两个专栏导航。读者可以自行选择前往哪个专栏。 (一)WIn32 专栏导航 上一篇:编程技能:格式化打印04,sprintf 回到目录…...

MPLAB X IDE 软件安装与卸载
1、下载MPLAB X IDE V6.25 MPLAB X IDE | Microchip Technology 正常选Windows,点击Download,等待自动下载完成; MPLAB X IDE 一台电脑上可以安装多个版本; 2、安装MPLAB X IDE V6.25 右键以管理员运行;next; 勾选 I a…...

windows编程实现文件拷贝
项目源码链接: 实现文件拷贝功能(限制5GB大小) 81c57de 周不才/cpp_linux study - Gitee.com 知识准备: 1.句柄 句柄是一个用于标识和引用系统资源(如文件、窗口、进程、线程、位图等)的值。它不是资…...
[6-01-01].第12节:字节码文件内容 - 属性表集合
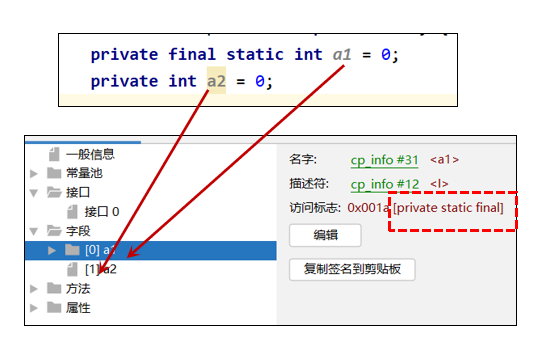
JVM学习大纲 二、属性表集合: 2.1.属性计数器: 2.2.属性表: 2.3.字节码文件组成5 -> 属性: 1.属性主要指的是类的属性,比如源码的文件名、内部类的列表等 2.4.字节码文件组成3 -> 字段: 1.字段中…...

基于机器学习的水量智能调度研究
摘要:随着城市化进程的加速和水资源供需矛盾的日益突出,传统的水量调度模式因缺乏精准预测和动态调控能力,难以满足现代供水系统对高效性、稳定性和节能性的要求。本文针对供水系统中用水峰谷预测不准确、能耗高、供需失衡等核心问题…...

深度解码:我如何用“结构进化型交互学习方法”与AI共舞,从学习小白到构建复杂认知体系
嗨,亲爱的学习者们,思考者们,以及所有渴望在知识海洋中自由翱行却时常感到迷茫的朋友们: 你是否也曾有过这样的深夜,面对堆积如山的学习资料,眼神迷离,内心却一片荒芜?明明每个字都…...

深入浅出 Scrapy:打造高效、强大的 Python 网络爬虫
在数据为王的时代,高效获取网络信息是开发者必备的技能。今天我将为大家介绍 Python 爬虫领域的王者框架——Scrapy。无论你是数据工程师、分析师还是开发者,掌握 Scrapy 都能让你的数据采集效率提升数倍! 项目地址:https://github.com/scrapy/scrapy 官方文档:https://do…...

ES6 Promise 状态机
状态机:抽象的计算模型,根据特定的条件或者信号切换不同的状态 一、Promise 是什么? 简单来说,Promise 就是一个“承诺对象”。在ES6 里,有些代码执行起来需要点时间,比如加载文件、等待网络请求或者设置…...

Axure 与 Cursor 集成实现方案
Axure 与 Cursor 集成实现方案 以下是一个完整的 Axure 与 Cursor AI 集成的原型实现方案,通过自定义 JavaScript 代码实现无缝对接: 一、整体架构设计 #mermaid-svg-f9hQDSN4hijU3mJY {font-family:"trebuchet ms",verdana,arial,sans-seri…...
