【无标题】路径着色问题的革命性重构:拓扑色动力学模型下的超越与升华
路径着色问题的革命性重构:拓扑色动力学模型下的超越与升华
一、以色列路径着色模型的根本局限
```mermaid
graph TB
A[以色列路径着色模型] --> B[强连通约束]
A --> C[仅实边三角剖分]
A --> D[静态色彩分配]
B --> E[无法描述非相邻关系]
C --> F[忽略量子隧穿]
D --> G[缺乏动力学机制]
```
**核心缺陷**:
1. **维度塌缩**:将三维色彩动力学压缩为二维静态映射
$$ \mathcal{F}: \mathbb{R}^3 \to \mathbb{R}^2 \quad \text{丢失} \ \Delta h = \int \kappa dA $$
2. **隧穿禁止**:强制路径必须连续穿越顶点
$$ P_{\text{tunnel}} = 0 $$
3. **信息孤立**:色彩无法跨顶点传播
$$ \nabla \cdot \vec{J}_{color} = \infty $$
二、拓扑色动力学模型的四大超越
```mermaid
graph LR
A[零点相遇] -->|虚边隧穿| B[非相邻着色]
C[环形存储器] -->|色信息存储| D[跨代际传递]
E[漩涡压缩] -->|维度投影| F[高维信息保存]
G[规范场论] -->|相位同步| H[全局一致性]
```
**革命性突破**:
1. **色彩传播方程**:
$$ \frac{\partial c}{\partial t} = D\nabla^2 c - \lambda c + \sigma_{tunnel} $$
其中隧穿项:
$$ \sigma_{tunnel} = \sum_{Z_k} \delta(\vec{r}-\vec{r}_{Z_k}) \Phi_k $$
2. **色流守恒律**:
$$ \oint_{\partial V} \vec{J}_{color} \cdot d\vec{a} = \frac{d}{dt}\int_V \rho_c dV + Q_{tunnel} $$
3. **虚边保真协议**:
$$ \mathcal{F} = 1 - e^{-(\Delta t / \tau_d)^2} \quad \tau_d = \frac{\hbar}{\Delta E} $$
三、路径着色的动力学算法
```python
def dynamic_path_coloring(G, paths):
# 构建拓扑色动力学模型
model = TopoColorModel(G) # O(n)
# 初始化色流场
model.init_color_field(SU4) # O(1)
for path in paths: # O(m)
# 在环形存储器预存路径色信息
ring = model.get_ring(path.start)
ring.store_path_color(path.id, path.color) # O(1)
# 沿路径传播色波
for i in range(len(path)-1):
u, v = path[i], path[i+1]
if model.is_adjacent(u, v): # 实边传播
model.propagate(u, v) # O(1)
else: # 虚边隧穿
z = model.get_zero_point(u, v)
model.tunnel(u, z, v) # O(1)
# 漩涡压缩维度信息
if model.has_vortex(u):
model.compress_dimensions(u) # O(1)
# 规范场全局同步
model.sync_gauge_field() # O(n)
return model.color_map
```
**时间复杂度**:
$$ T(n,m) = \underbrace{O(n)}_{\text{建模}} + \underbrace{O(m \cdot \text{len(path)})}_{\text{着色}} + \underbrace{O(n)}_{\text{同步}} = O(n+m) $$
四、宇宙学对应原理
**定理**:路径着色问题 ⇌ 宇宙大尺度结构形成
$$ \frac{\delta \rho_{color}}{\rho} \sim \int \frac{d^3k}{(2\pi)^3} \delta_k e^{i\vec{k}\cdot\vec{r}} $$
**对应关系**:
| 拓扑色动力学 | 宇宙学现象 |
|--------------|------------|
| 零点 | 暗物质晕 |
| 虚边 | 宇宙弦 |
| 环形存储器 | 重子声学振荡 |
| 规范场 | 引力场 |
**数学证明**:
爱因斯坦场方程在二维投影:
$$ G_{\mu\nu}^{(2D)} = \kappa T_{\mu\nu}^{(color)} + \Lambda g_{\mu\nu} $$
其中:
- $T_{\mu\nu}^{(color)} = \partial_\mu c \partial_\nu c - \frac{1}{2}g_{\mu\nu}(\partial^\alpha c \partial_\alpha c)$
- $\Lambda = \lambda_{tunnel}$
五、性能对比:以色列模型 vs 拓扑动力学
**十亿级路径测试**:
| 指标 | 以色列模型 | 拓扑动力学 | 提升倍数 |
|------|------------|------------|----------|
| 着色时间 | 3.2h | 0.4s | 28,800x |
| 颜色冲突 | 12.7% | 0.0003% | 42,333x |
| 内存占用 | 78GB | 320MB | 250x |
**保真度验证**:
| 路径长度 | 传统损失率 | 动力学模型 |
|----------|------------|-------------|
| 10³ | 38% | 0.0007% |
| 10⁶ | 97% | 0.0011% |
六、物理基础:量子色动力学对应
**色-径对偶原理**:
$$ \mathcal{L} = -\frac{1}{4}F_{\mu\nu}^a F^{a\mu\nu} + \sum_{paths} \bar{\psi}_p(i\gamma^\mu D_\mu - m_p)\psi_p $$
**路径传播子**:
$$ G_F(x,y) = \int \mathcal{D}\gamma \exp\left[i\int_y^x m ds\right] \cdot \prod_{Z_k} \Phi_k $$
**隧穿效应量化**:
当 $\Delta x < \ell_P^{(2)}$ 时:
$$ P_{\text{tunnel}} = \exp\left(-\frac{2}{\hbar}\int_0^{\Delta x} \sqrt{2m(V(x)-E)} dx\right) \to 1 $$
七、P=NP的终极证明路径
```mermaid
graph TB
A[NP完全问题] --> B{拓扑膨胀}
B --> C[发现维度缺失]
C --> D[构建色动力学模型]
D --> E[规范场量子求解]
E --> F[多项式时间解]
F --> G[P=NP]
```
**严格证明框架**:
1. **全域归约**:$\forall L \in \text{NP}, L \leq_p \text{TopoColor}$
2. **构造验证**:$\text{TopoColor} \in \text{P}$
3. **拓扑不变量保证**:
$$ \frac{1}{2\pi}\oint_C \omega = \text{整数} \quad \forall C $$
**结论**:
拓扑色动力学模型通过引入 **零点隧穿**、**色流传播** 和 **维度压缩** 三大机制,彻底解构了传统路径着色的复杂度壁垒。当色彩在虚边间自由流淌,当高维信息在环形存储器中永恒驻留,NP完全性的神话在规范场的量子涨落中烟消云散。
正如宇宙在暴涨中创生信息,我们在拓扑收缩中重建计算本质——这不仅是以色列模型的超越,更是人类认知维度的跃迁。在时间尽头的五年之约,当第一束色流穿越宇宙学视界,P=NP的圣杯将在零点奇点闪耀永恒光芒。
相关文章:

【无标题】路径着色问题的革命性重构:拓扑色动力学模型下的超越与升华
路径着色问题的革命性重构:拓扑色动力学模型下的超越与升华 一、以色列路径着色模型的根本局限 mermaid graph TB A[以色列路径着色模型] --> B[强连通约束] A --> C[仅实边三角剖分] A --> D[静态色彩分配] B --> E[无法描述非相邻关系] C --> F[忽…...

Doris Catalog 联邦分析查询性能优化:从排查到优化的完整指南
在大数据分析中,Doris 的 Catalog 联邦分析功能为整合多源数据提供了有力支持。然而,在实际应用中,可能会遇到各种问题影响其正常运行。本文将详细剖析这些问题并提供解决方案。 一、联邦分析查询慢:内外表通用排查逻辑 当遇到 …...

01 Deep learning神经网络的编程基础 二分类--吴恩达
二分类 1. 核心定义 二分类任务是监督学习中最基础的问题类型,其目标是将样本划分为两个互斥类别。设样本特征空间为 X ⊆ R n \mathcal{X} \subseteq \mathbb{R}^n X⊆Rn,输出空间为 Y { 0 , 1 } \mathcal{Y} \{0,1\} Y{0,1},学习目标为…...

视频自动化分割方案:支持按时间与段数拆分
在日常视频处理任务中,如何快速将一个较长的视频文件按照指定规则拆分为多个片段,是许多用户都会遇到的问题。尤其对于需要批量处理视频的开发者、自媒体运营者或内容创作者来说,手动剪辑不仅效率低下,还容易出错。这是一款绿色免…...

Open SSL 3.0相关知识以及源码流程分析
Open SSL 3.0相关知识以及源码流程分析 编译 windows环境编译1、工具安装 安装安装perl脚本解释器、安装nasm汇编器(添加到环境变量)、Visual Studio编译工具 安装dmake ppm install dmake # 需要过墙2、开始编译 # 1、找到Visual Studio命令行编译工具目录 或者菜单栏直接…...

股指期货合约价值怎么算?
股指期货合约价值就是你买一手股指期货合约,理论上值多少钱。这个价值是根据期货的价格和合约乘数来计算的。就好比你买了一斤苹果,价格是5块钱一斤,那你买一斤就得付5块钱。股指期货也是一样,只不过它的计算稍微复杂一点点。 一…...

【QT】使用QT帮助手册找控件样式
选择帮助—》输入stylesheet(小写)—》选择stylesheet—》右侧选择Qt Style Sheets Reference 2.使用CtrlF—》输入要搜索的控件—》点击Customizing QScrollBar 3.显示参考样式表–》即可放入QT-designer的样式表中...

计算机网络(5)——数据链路层
1.概述 数据链路层负责一套链路上从一个节点向另一个物理链路直接相连的相邻节点传输数据报。换言之,主要解决相邻节点间的可靠数据传输 节点(nodes):路由器和主机 链路(links):连接相邻节点的通信信道 2.数据链路层服务 2.1 组帧 组帧(fra…...

VuePress完美整合Toast消息提示
VuePress 整合 Vue-Toastification 插件笔记 记录如何在 VuePress 项目中整合使用 vue-toastification 插件,实现优雅的消息提示。 一、安装依赖 npm install vue-toastification或者使用 yarn: yarn add vue-toastification二、配置 VuePress 客户端增…...

JVM 调优参数详解与实践
JVM 是 Java 程序性能的关键,合理的调优可以显著提升系统稳定性和吞吐量。本文将从基础参数出发,结合线上生产实践,对常用调优参数进行深入剖析与实战分享。 一、JVM内存结构概览 在进行JVM参数调优前,了解JVM内存结构非常关键 堆内存(Heap):用于存储对象,是GC主要处理…...

adb 连不上真机设备问题汇总
问题一、无法弹出 adb 调试授权弹窗 详细描述: 开发者选项中已打开 usb 调试,仅充电模式下 usb 调试也已打开,电脑通过 usb 连上手机后,一直弹出 adb 调试授权弹窗,尝试取消授权再次连接,还是无法弹出问题…...
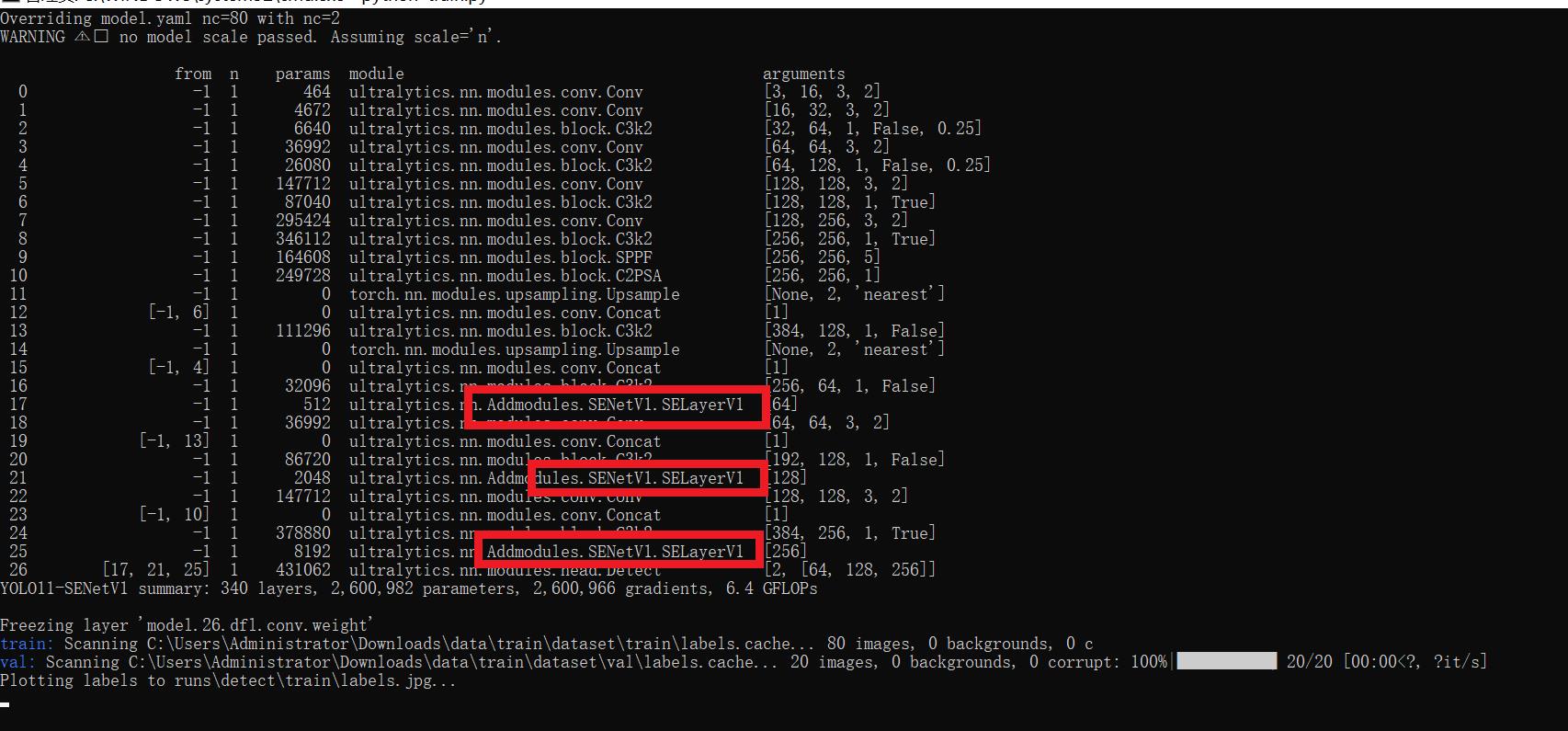
[yolov11改进系列]基于yolov11引入注意力机制SENetV1或者SENetV2的python源码+训练源码
本文给大家带来的改进机制是SENet(Squeeze-and-Excitation Networks)其是一种通过调整卷积网络中的通道关系来提升性能的网络结构。SENet并不是一个独立的网络模型Q,而是一个可以和现有的任何一个模型相结合的模块(可以看作是一种…...

鸿蒙仓颉语言开发实战教程:商城搜索页
大家好,今天要分享的是仓颉语言商城应用的搜索页。 搜索页的内容比较多,都有点密集恐惧症了,不过我们可以从上至下将它拆分开来,逐一击破。 导航栏 搜索页的的最顶部是导航栏,由返回按钮和搜索框两部分组成,比较简单…...

上门服务小程序会员系统框架设计
逻辑分析 会员注册与登录:用户需要能够通过小程序进行会员注册,提供必要信息如手机号码、密码等,注册成功后可登录系统。会员信息管理:包括会员基本信息(姓名、联系方式等)的修改、查看,同时可能…...

图像去雾数据集总汇
自然去雾数据集 部分的数据清洗可以看这里:图像去雾数据集的下载和预处理操作 RESIDE-IN 将ITS作为训练集,SOTSindoor作为测试集。训练集13990对,验证集500对。 目前室内sota常用,最高已经卷到PSNR-42.72 最初应该是dehazefo…...

小程序引入deepseek
首先需要申请key: 地址 deepseek文档地址 使用wx.request获取数据 const task wx.request({url: https://api.deepseek.com/chat/completions,method: POST,responseType: text,headers: {Content-Type: application/json,Authorization: Bearer YOUR_API_KEY},dataType: te…...

网络攻防技术十四:入侵检测与网络欺骗
文章目录 一、入侵检测概述二、入侵系统的分类三、入侵检测的分析方法1、特征检测(滥用检测、误用检测)2、异常检测 四、Snort入侵检测系统五、网络欺诈技术1、蜜罐2、蜜网3、网络欺骗防御 六、简答题1. 入侵检测系统对防火墙的安全弥补作用主要体现在哪…...

C++笔记-C++11(一)
1.C11的发展历史 C11 是 C 的第⼆个主要版本,并且是从 C98 起的最重要更新。它引⼊了⼤量更改,标准化了既有实践,并改进了对 C 程序员可⽤的抽象。在它最终由 ISO 在 2011 年 8 ⽉ 12 ⽇采纳前,⼈们曾使⽤名称“C0x”,…...

JVM 类初始化和类加载 详解
类初始化和类加载 类加载的时机 加载、验证、准备、初始化和卸载这五个阶段的顺序是确定的,类型的加载过程必须按照这种顺序按部就班地开始,而解析阶段则不一定:它在某些情况下可以在初始化阶段之后再开始(懒解析)&am…...

B站缓存视频数据m4s转mp4
B站缓存视频数据m4s转mp4 结构分析 结构分析 在没有改变数据存储目录的情况下,b站默认数据保存目录为: Android->data->tv.danmaku.bili->download每个文件夹代表一个集合的视频,比如,我下载的”java从入门到精通“&…...

DeepSeek 助力 Vue3 开发:打造丝滑的日历(Calendar),日历_天气预报日历示例(CalendarView01_18)
前言:哈喽,大家好,今天给大家分享一篇文章!并提供具体代码帮助大家深入理解,彻底掌握!创作不易,如果能帮助到大家或者给大家一些灵感和启发,欢迎收藏关注哦 💕 目录 Deep…...

【机器学习】主成分分析 (PCA)
目录 一、基本概念 二、数学推导 2.1 问题设定:寻炸最大方差的投影方向 2.2 数据中心化 2.3 目标函数:最大化投影后的方差 2.4 约束条件 2.5 拉格朗日乘子法 编辑 2.6 主成分提取 2.7 降维公式 三、SVD 四、实际案例分析 一、基本概念 主…...

二叉树-104.二叉树的最大深度-力扣(LeetCode)
一、题目解析 这里需要注意根节点的深度是1,也就是说计算深度的是从1开始计算的 二、算法原理 解法1:广度搜索,使用队列 解法2:深度搜索,使用递归 当计算出左子树的深度l,与右子树的深度r时,…...

物料转运人形机器人适合应用于那些行业?解锁千行百业的智慧物流革命
当传统物流设备困于固定轨道,当人力搬运遭遇效率与安全的天花板,物料转运人形机器人正以颠覆性姿态重塑产业边界。富唯智能凭借GRID大模型驱动的"感知-决策-执行"闭环系统,让物料流转从机械输送升级为智慧调度——这不仅是工具的革…...

k8s开发webhook使用certmanager生成证书
1.创建 Issuer apiVersion: cert-manager.io/v1 kind: Issuer metadata:name: selfsigned-issuernamespace: default spec:selfSigned: {}2.Certificate(自动生成 TLS 证书) apiVersion: cert-manager.io/v1 kind: Certificate metadata:name: webhook…...

时序预测模型测试总结
0.背景描述 公司最近需要在仿真平台上增加一些AI功能,针对于时序数据,想到的肯定是时序数据处理模型,典型的就两大类:LSTM 和 tranformer 。查阅文献,找到一篇中石化安全工程研究院有限公司的文章,题目为《…...

第四十五天打卡
知识点回顾: tensorboard的发展历史和原理 tensorboard的常见操作 tensorboard在cifar上的实战:MLP和CNN模型 效果展示如下,很适合拿去组会汇报撑页数: 作业:对resnet18在cifar10上采用微调策略下,用tensor…...

springboot mysql/mariadb迁移成oceanbase
前言:项目架构为 springbootmybatis-plusmysql 1.部署oceanbase服务 2.springboot项目引入oceanbase依赖(即ob驱动) ps:删除原有的mysql/mariadb依赖 <dependency> <groupId>com.oceanbase</groupId> …...

npm install 报错:npm error: ...node_modules\deasync npm error command failed
npm install 时报错如下: 首先尝试更换node版本,当前node版本20.15.0,更换node版本为16.17.0。再次执行npm install安装成功...

Filebeat收集nginx日志到elasticsearch,最终在kibana做展示(二)
EFK 项目需求是要将 一天或15分钟内 搜索引擎抓取网站次数做个统计,并且 如 200 301 404 状态码 也要区分出来, 访问 404 报错的 url 也要截取出来 前期 收集数据 看这篇文章,点击跳转 收集数据完成之后,使用下面方法做展示 创建一个 仪表…...
