矩阵分解相关知识点总结(二)
文章目录
- 三、矩阵的QR分解
- 3.1、Givens矩阵与Givens变换
- 3.2、Householder矩阵与Householder变换
- 3.3、QR分解
书接上文矩阵分解相关知识点总结(一)
三、矩阵的QR分解
3.1、Givens矩阵与Givens变换
设非零列向量 x ∈ R n \bm{x}\in {\bf{R}}^n x∈Rn及单位列向量 z ∈ R n \bm{z}\in {\bf{R}}^n z∈Rn,存在有限个Givens矩阵的乘积,记作 T \bm{T} T,使得
T x = ∣ x ∣ z (3) \color{#F00}\bm{T}\bm{x}=|\bm{x}|\bm{z}\tag{3} Tx=∣x∣z(3)
上式即为Givens变换,也称初等旋转变换,其中Givens矩阵,也称初等旋转矩阵,记作 T i j = T i j ( c , s ) = [ I c s I − s c I ] \color{#F0F}\bm{T}_{ij}=\bm{T}_{ij}(c,s)=\begin{bmatrix} \bm{I} \\[1ex] & c & & s & \\[1.2ex] & & \bm{I} \\[1.2ex] & -s& & c \\[1.2ex] & & & & \bm{I} \end{bmatrix} Tij=Tij(c,s)= Ic−sIscI , T = T 1 n T 1 , n − 1 ⋯ T 13 T 12 \bm{T}=\bm{T}_{1n}\bm{T}_{1,n-1}\cdots \bm{T}_{13}\bm{T}_{12} T=T1nT1,n−1⋯T13T12。
对于非零列向量 x = ( ξ 1 , ξ 2 , ⋯ , ξ n ) T \bm{x}=(\xi_1,\xi_2,\cdots,\xi_n)^{\rm T} x=(ξ1,ξ2,⋯,ξn)T,及单位列向量 z = e 1 = ( 1 , 0 , ⋯ , 0 ) T \bm{z}=\bm{e}_1=(1,0,\cdots,0)^{\rm T} z=e1=(1,0,⋯,0)T,其Givens变换过程如下:
-
首先对 x \bm{x} x构造Givens矩阵 T 12 ( c , s ) = [ c s − s c I ] \bm{T}_{12}(c,s)=\begin{bmatrix} c&s \\-s & c\\ & & \bm{I} \end{bmatrix} T12(c,s)= c−sscI ,其中 c = ξ 1 ξ 1 2 + ξ 2 2 , s = ξ 2 ξ 1 2 + ξ 2 2 c=\cfrac{\xi_1}{\sqrt{\xi_1^2+\xi_2^2}}\,,\,s=\cfrac{\xi_2}{\sqrt{\xi_1^2+\xi_2^2}} c=ξ12+ξ22ξ1,s=ξ12+ξ22ξ2,有
T 12 x = ( ξ 1 2 + ξ 2 2 , 0 , ξ 3 , ⋯ , ξ n ) T \bm{T}_{12}\bm{x}=(\sqrt{\xi_1^2+\xi_2^2},0,\xi_3,\cdots,\xi_n)^{\rm T} T12x=(ξ12+ξ22,0,ξ3,⋯,ξn)T -
再对 T 12 x \bm{T}_{12}\bm{x} T12x构造Givens矩阵 T 13 ( c , s ) = [ c s 1 − s c I ] \bm{T}_{13}(c,s)=\begin{bmatrix} c& &s \\ &1& \\-s & & c\\ & & & \bm{I} \end{bmatrix} T13(c,s)= c−s1scI ,其中 c = ξ 1 2 + ξ 2 2 ξ 1 2 + ξ 2 2 + ξ 3 2 , s = ξ 3 ξ 1 2 + ξ 2 2 + ξ 3 2 c=\cfrac{\sqrt{\xi_1^2+\xi_2^2}}{\sqrt{\xi_1^2+\xi_2^2+\xi_3^2}}\,,\,s=\cfrac{\xi_3}{\sqrt{\xi_1^2+\xi_2^2+\xi_3^2}} c=ξ12+ξ22+ξ32ξ12+ξ22,s=ξ12+ξ22+ξ32ξ3,有
T 13 ( T 12 x ) = ( ξ 1 2 + ξ 2 2 + ξ 3 2 , 0 , 0 , ξ 4 , ⋯ , ξ n ) T \bm{T}_{13}(\bm{T}_{12}\bm{x})=(\sqrt{\xi_1^2+\xi_2^2+\xi_3^2},0,0,\xi_4,\cdots,\xi_n)^{\rm T} T13(T12x)=(ξ12+ξ22+ξ32,0,0,ξ4,⋯,ξn)T -
如此下去,最后对 T 1 , n − 1 T 1 , n − 2 ⋯ T 13 T 12 x \bm{T}_{1,n-1}\bm{T}_{1,n-2}\cdots \bm{T}_{13}\bm{T}_{12}\bm{x} T1,n−1T1,n−2⋯T13T12x构造Givens矩阵 T 1 n ( c , s ) = [ c s I − s c ] \bm{T}_{1n}(c,s)=\begin{bmatrix} c& &s \\ & \bm{I}& \\-s & & c \end{bmatrix} T1n(c,s)= c−sIsc ,其中 c = ξ 1 2 + ⋯ + ξ n − 1 2 ξ 1 2 + ξ 2 2 + ⋯ + ξ n − 1 2 + ξ n 2 , s = ξ n ξ 1 2 + ξ 2 2 + ⋯ + ξ n − 1 2 + ξ n 2 \color{#F0F}c=\cfrac{\sqrt{\xi_1^2+\cdots+\xi_{n-1}^2}}{\sqrt{\xi_1^2+\xi_2^2+\cdots+\xi_{n-1}^2+\xi_{n}^2}}\,,\,s=\cfrac{\xi_n}{\sqrt{\xi_1^2+\xi_2^2+\cdots+\xi_{n-1}^2+\xi_{n}^2}} c=ξ12+ξ22+⋯+ξn−12+ξn2ξ12+⋯+ξn−12,s=ξ12+ξ22+⋯+ξn−12+ξn2ξn,有
T 1 n ( T 1 , n − 1 ⋯ T 12 x ) = ( ξ 1 2 + ξ 2 2 + ⋯ + ξ n − 1 2 + ξ n 2 , 0 , ⋯ , 0 ) T \bm{T}_{1n}(\bm{T}_{1,n-1}\cdots \bm{T}_{12}\bm{x})=(\sqrt{\xi_1^2+\xi_2^2+\cdots+\xi_{n-1}^2+\xi_{n}^2},0,\cdots,0)^{\rm T} T1n(T1,n−1⋯T12x)=(ξ12+ξ22+⋯+ξn−12+ξn2,0,⋯,0)T
令 T = T 1 n T 1 , n − 1 ⋯ T 12 \bm{T}=\bm{T}_{1n}\bm{T}_{1,n-1}\cdots \bm{T}_{12} T=T1nT1,n−1⋯T12,有 T x = ∣ x ∣ z = ∣ x ∣ e 1 \bm{T}\bm{x}=|\bm{x}|\bm{z}=|\bm{x}|\bm{e}_1 Tx=∣x∣z=∣x∣e1,即通过有限个Givens矩阵 T \bm{T}\, T将 x \bm{x}\, x变换为与 z \bm{z}\, z同方向的向量。
3.2、Householder矩阵与Householder变换
任意给定非零列向量 x ∈ R n ( n > 1 ) \bm{x}\in {\bf{R}}^n\;(n>1) x∈Rn(n>1)及单位列向量 z ∈ R n \bm{z}\in {\bf{R}}^n z∈Rn,则存在矩阵 H \bm{H} H,使得
H x = ∣ x ∣ z (4) \color{#F00}\bm{H}\bm{x}=|\bm{x}|\bm{z}\tag{4} Hx=∣x∣z(4)
上式即为Householder变换,也称初等反射变换,其中 H = I − 2 u u T \color{#F0F}\bm{H}=\bm{I}-2\bm{uu}^{\rm T} H=I−2uuT,为Householder矩阵,也称初等反射矩阵。
对于非零列向量 x = ( ξ 1 , ξ 2 , ⋯ , ξ n − 1 , ξ n ) T \bm{x}=(\xi_1,\xi_2,\cdots,\xi_{n-1},\xi_n)^{\rm T} x=(ξ1,ξ2,⋯,ξn−1,ξn)T及单位列向量 z = e 1 = ( 1 , 0 , ⋯ , 0 ) T \bm{z}=\textbf{\textit{e}}_1=(1,0,\cdots,0)^{\rm T} z=e1=(1,0,⋯,0)T,其Householder变换过程如下:
取 u = x − ∣ x ∣ z ∣ x − ∣ x ∣ z ∣ = x − ∣ x ∣ e 1 ∣ x − ∣ x ∣ e 1 ∣ \color{#F0F}\bm{u}=\cfrac{\bm{x}-|\bm{x}|\bm{z}}{|\bm{x}-|\bm{x}|\bm{z}|}=\cfrac{\bm{x}-|\bm{x}|\bm{e}_1}{|\bm{x}-|\bm{x}|\bm{e}_1|} u=∣x−∣x∣z∣x−∣x∣z=∣x−∣x∣e1∣x−∣x∣e1,其中 ∣ x ∣ = ξ 1 2 + ξ 2 2 + ⋯ + ξ n − 1 2 + ξ n 2 |\bm{x}|=\sqrt{\xi_1^2+\xi_2^2+\cdots+\xi_{n-1}^2+\xi_{n}^2} ∣x∣=ξ12+ξ22+⋯+ξn−12+ξn2,则 H = I − 2 u u T \bm{H}=\bm{I}-2\bm{uu}^{\rm T} H=I−2uuT, H x = ∣ x ∣ z = ∣ x ∣ e 1 \bm{Hx}=|\bm{x}|\bm{z}=|\bm{x}|\bm{e}_1 Hx=∣x∣z=∣x∣e1,即通过Householder矩阵 H \bm{H}\, H将 x \bm{x}\, x变换为与 z \bm{z}\, z同方向的向量。
| Givens矩阵 T i j \textbf{\textit{T}}_{ij}\, Tij具有如下性质 | Householder矩阵 H \textbf{\textit{H}}\, H具有如下性质 | |
|---|---|---|
| (1) | T i j = − T i j T = − T i j − 1 \bm{T}_{ij}=-\bm{T}_{ij}^{\rm T}=-\bm{T}_{ij}^{-1} Tij=−TijT=−Tij−1 | H = H T = H − 1 \bm{H}=\bm{H}^{\rm T}=\bm{H}^{-1} H=HT=H−1 |
| (2) | T i j 2 = − T i j T T i j = − T i j − 1 T i j = − I \bm{T}_{ij}^{2}=-\bm{T}_{ij}^{\rm T}\bm{T}_{ij}=-\bm{T}_{ij}^{-1}\bm{T}_{ij}=-\bm{I} Tij2=−TijTTij=−Tij−1Tij=−I | H 2 = H T H = H − 1 H = I \bm{H}^2=\bm{H}^{\rm T}\bm{H}=\bm{H}^{-1}\bm{H}=\bm{I} H2=HTH=H−1H=I |
| (3) | d e t T i j = 1 \rm{det}\bm{T}_{ij}=1 detTij=1 | d e t H = − 1 \rm{det}\bm{H}=-1 detH=−1 |
初等旋转矩阵是两个初等反射矩阵的乘积,即有 T i j = H v H u (5) \color{#F00}初等旋转矩阵是两个初等反射矩阵的乘积,即有\bm{T}_{ij}=\bm{H}_v\bm{H}_u\tag{5} 初等旋转矩阵是两个初等反射矩阵的乘积,即有Tij=HvHu(5)
3.3、QR分解
设 A A A是 m × n m\times n m×n实(复)矩阵,且其 n n n个列线性无关,则 A A A有分解
A = Q R (6) \color{#F00}A=QR\tag{6} A=QR(6)
其中 Q Q Q是 m × n m\times n m×n实(复)矩阵,且满足 Q T Q = I Q^{\text T}Q=I QTQ=I( Q H Q = I Q^{\text H}Q=I QHQ=I), R R R是 n n n阶实(复)可逆上三角矩阵。上式即为矩阵的QR分解,也称正交三角分解,该分解除去相差一个对角元素的绝对值(模)全等于1的对角矩阵因子外是唯一的。
对于任意的 n n n阶实可逆矩阵 A = ( a i j ) n × n A=(a_{ij})_{n \times n} A=(aij)n×n,均可通过左连乘Givens矩阵(初等旋转矩阵)或左连乘Householder矩阵(初等反射矩阵),将其化为可逆上三角矩阵。
相关文章:
)
矩阵分解相关知识点总结(二)
文章目录 三、矩阵的QR分解3.1、Givens矩阵与Givens变换3.2、Householder矩阵与Householder变换3.3、QR分解 书接上文矩阵分解相关知识点总结(一) 三、矩阵的QR分解 3.1、Givens矩阵与Givens变换 设非零列向量 x ∈ R n \bm{x}\in {\bf{R}}^n x∈Rn及单…...

MySQL——视图 用户管理 语言访问
目录 视图 用户管理 数据库权限 访问 准备工作 使用函数 mysql界面级工具 连接池 视图 这里的视图与事务中的读视图是两个不同的概念:视图是一个虚拟表,其内容由查询定义。同真实的表一样,视图包含一系列带有名称的列和行数据。视图的…...

二、Sqoop 详细安装部署教程
作者:IvanCodes 日期:2025年6月2日 专栏:Sqoop教程 Apache Sqoop 是一个强大的工具,用于在 Hadoop (HDFS, Hive, HBase) 与关系型数据库 (如 MySQL, PostgreSQL, Oracle) 之间高效传输数据。本教程将详细指导您如何根据官方网站截…...

用Python开启游戏开发之旅
在当今丰富多彩的数字娱乐世界中,游戏以其独特的魅力吸引着无数人的目光。而Python这门功能强大又简洁易懂的编程语言,也为游戏开发打开了一扇充满创意的大门。 一、选择Python的理由 Python之所以备受游戏开发者青睐,有诸多原因。其一&#…...

React 第五十四节 Router中useRevalidator的使用详解及案例分析
前言 useRevalidator 是 React Router v6.4 引入的一个强大钩子,用于在数据路由(Data Router)中手动触发路由数据的重新验证(revalidation)。 它在需要主动刷新数据而不改变路由位置的场景中非常有用。 一、useReval…...

【C语言预处理详解(下)】--#和##运算符,命名约定,命令行定义 ,#undef,条件编译,头文件的包含,嵌套文件包含,其他预处理指令
目录 五.#和##运算符 5.1--#运算符 5.2--##运算符 六.命名约定,#undef,命令行定义 6.1--命名约定 6.2--#undef 6.3--命名行定义 七.条件编译 常见的条件编译指令: 1.普通的条件编译: 2.多个分支的条件编译(可以利用条…...

03.搭建K8S集群
K8S集群搭建的方式 目前主流的搭建k8s集群的方式有kubeadm、minikube、二进制包三种方式: kubeadm(本案例搭建方式) 是一个工具,用于快速搭建kubernetes集群,目前应该是比较方便和推荐的,简单易用 kubea…...

RDMA简介3之四种子协议对比
RDMA协议共有四种子协议,分别为InfiniBand、iWARP、RoCE v1和RoCE v2协议。这四种协议使用统一的RDMA API,但在具体的网络层级实现上有所不同,如图1所示,接下来将分别介绍这四种子协议。 图1 RDMA四种子协议网络层级关系图 Infin…...
【最新版】西陆洗车系统源码全开源+uniapp前端+搭建教程
一.系统介绍 一款基于ThinkPHPUniapp开发的多门店洗车系统,包含用户端(小程序)、门店员工端(小程序)、门店端(PC)、平台管理端(PC)。 门店分连锁门店和独立门店…...

力扣LeetBook数组和字符串--二维数组
1.旋转矩阵 题目链接 想了那么久的各种旋转,对角线,其实把问题搞复杂了。 旋转90度的本质无非就是转置镜像对称 转置是什么?:将矩阵的行和列互换。 镜像对称:把矩阵从中间对折,互换位置 矩阵 A A [ 1 3 0…...

Linux开发工具(apt,vim,gcc)
目录 yum/apt包管理器 Linux编辑器 vim 1.见一见vim 2.vim的多模式 3.命令模式底行模式等 4.vim的配置 Linux编译器 gcc/g 1.预处理(宏替换) 2.编译(生成汇编) 3.汇编(生成机器可识别代码) 4.连…...

C# ExcelWorksheet 贴图
C# ExcelWorksheet 贴图 在C#中,如果你想在Excel工作表中插入图片(例如,在ExcelWorksheet中贴图),你可以使用ClosedXML或EPPlus这样的库来操作Excel文件。下面我将分别介绍如何使用这两个库来实现这一功能。 使用ClosedXML 首先,确保你已经安装了ClosedXML包。你可以通…...

鸿蒙Next开发真机调试签名申请流程
背景: 在学习鸿蒙next开发应用的初期总是会遇到一堆的问题,毕竟鸿蒙next开发不管是他的ArKTS语言还是他的开发工具DevEco Studio都还在起步阶段,就像当初的Android起步一样,总会有资料不足的一些问题。就比如我们学习下载完DevEco…...
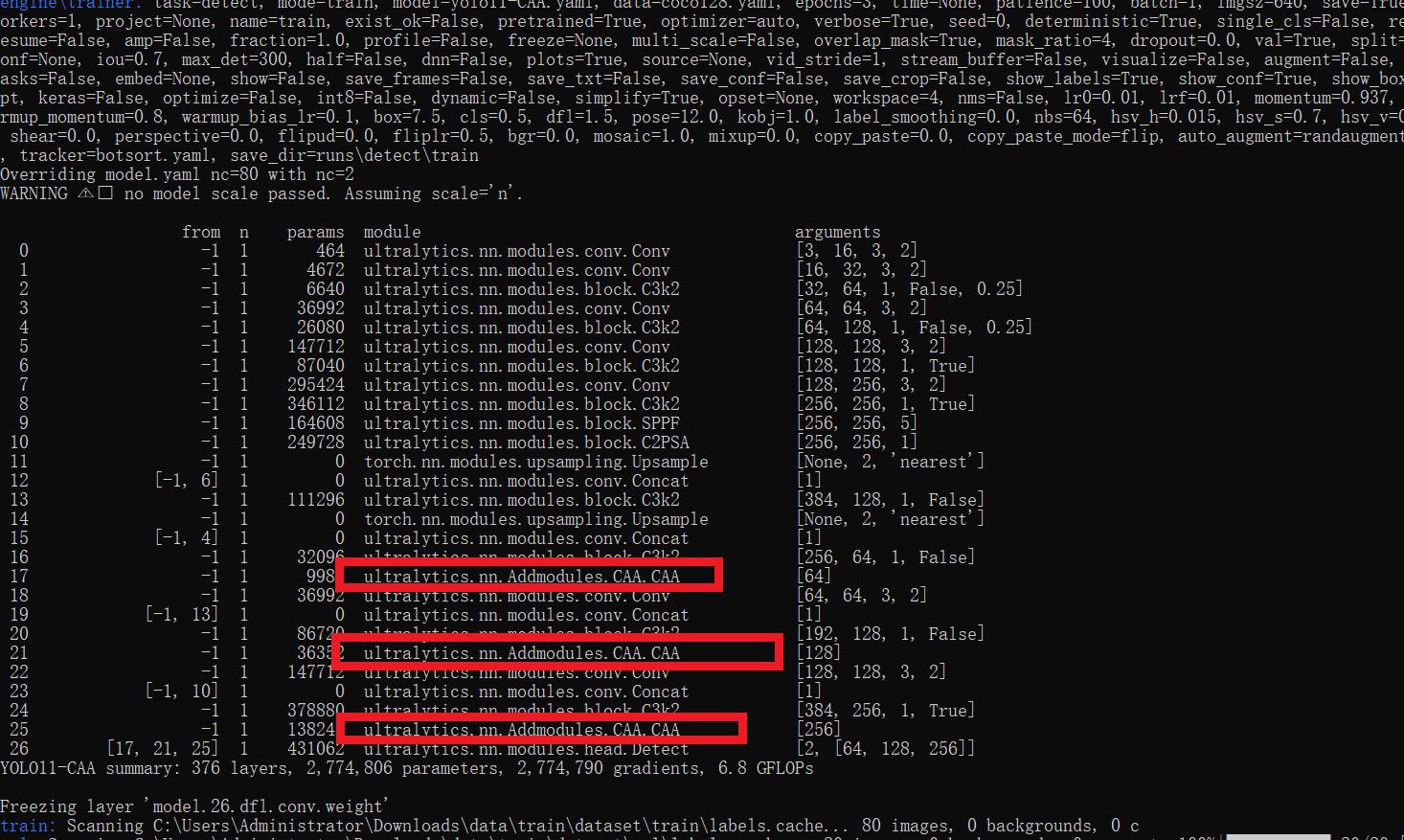
[yolov11改进系列]基于yolov11引入上下文锚点注意力CAA的python源码+训练源码
【CAA介绍】 本文记录的是基于CAA注意力模块的RT-DETR目标检测改进方法研究。在远程遥感图像或其他大尺度变化的图像中目标检测任务中,为准确提取其长距离上下文信息,需要解决大目标尺度变化和多样上下文信息时的不足的问题。CAA能够有效捕捉长距离依赖…...

【Elasticsearch】 查询优化方式
在优化Elasticsearch的查询性能时,可以从多个维度着手,包括索引设计、查询优化、集群配置、数据管理以及监控分析等。常见的优化方式和策略有以下几种: 一、索引优化 合理设计字段类型: 字段类型选择: 对于不需要分词的…...

Xcode 16.4 + iOS 18 系统运行时崩溃:___cxa_current_primary_exception 符号丢失的原因与解决方案
在使用 Xcode 16.4 构建项目,运行到 iOS 18.3 或更早版本系统(包括模拟器)时,出现了如下的运行时崩溃: dyld[22183]: Symbol not found: ___cxa_current_primary_exceptionReferenced from: /.../WidgetOn.app/Widget…...

【linux】全志Tina预编译一个so库文件到根文件系统/usr/lib/下
一、sdk中新建文件夹 路径: V:\t113\work3\t113\openwrt\package\feeds\libs\md5util md5util为需要注入的库文件夹。 文件结构 libs md5util files libmd5util.so makefile etc.. 二、编写makefile include $(TOPDIR)/rules.mkPKG_NAME : md5util PKG_VERSIO…...

C# 类和继承(成员访回修饰符)
成员访回修饰符 本章之前的两节阐述了类的可访问性。对类的可访问性,只有两种修饰符:internal和public。 本节阐述成员的可访问性。类的可访问性描述了类的可见性;成员的可访问性描述了类成员的可 见性。 声明在类中的每个成员对系统的不同…...

c++ stl容器之map用法
目录 (1)map介绍 (2)map、multimap、unordered_map区别 (3)map用法 1.map接口表 2.使用举例 插入数据与遍历数据 查找关键字和值 删除元素 按照值排序 (4)multimap用法 &…...

Linux-文件管理及归档压缩
1.根下的目录作用说明: /:Linux系统中所有的文件都在根下/bin:(二进制命令目录)存放常用的用户命令/boot:系统启动时的引导文件(内核的引导配置文件,grub配置文件,内核配置文件) 例…...

结合Jenkins、Docker和Kubernetes等主流工具,部署Spring Boot自动化实战指南
基于最佳实践的Spring Boot自动化部署实战指南,结合Jenkins、Docker和Kubernetes等主流工具,提供从环境搭建到生产部署的完整流程: 一、环境准备与工具选型 1.基础设施 Jenkins服务器:安装Jenkins LTS版本,配置JDK(推荐JDK 11+)及Maven/Gradle插…...

微软认证考试科目众多?该如何选择?
在云计算、人工智能、数据分析等技术快速发展的今天,微软认证(Microsoft Certification)已成为IT从业者、开发者、数据分析师提升竞争力的重要凭证。但面对众多考试科目,很多人不知道如何选择。本文将详细介绍微软认证的考试方向、…...

MCP协议在LLM系统中的架构与实现原理研究
MCP协议的角色和功能定位 模型上下文协议(Model Context Protocol, MCP) 是由Anthropic公司(Claude模型的发布方)提出的一种开放协议,旨在标准化大型语言模型(LLM)与外部数据源、工具和服务之间的交互方式。可以将MCP类比为AI应用的“USB-C接口”:通过统一的接口协议,…...

Dify工作流实践—根据word需求文档编写测试用例到Excel中
前言 这篇文章依赖到的操作可查阅我之前的文章: dify里的大模型是怎么添加进来的:在Windows本地部署Dify详细操作 flask 框架app.route()函数的开发和调用:PythonWeb开发框架—Flask工程创建和app.route使用详解 结构化提示词的编写&…...

【LC实战派】小智固件编译
这篇写给立创吴总,是节前答应他配合git代码的说明;也给所有对小智感兴趣的小伙伴。 请多提意见,让这份文档更有价值 - 第一当然是拉取源码 - git clone https://github.com/78/xiaozhi-esp32.git 完成后,先查看固件中实际的…...
详解)
HTTP(超文本传输协议)详解
目录 一、基本概念 二、HTTP报文(结构) (一) 请求报文 (二) 响应报文 三、HTTP请求方法 1. GET方法 2. POST方法 3. PUT方法 4. HEAD方法 5. DELETE 6. OPTIONS 一、知识扩展 7. TRACE 8. CONNECT 四、HTTP持久通信 (一) HTTP keep-alive…...

Unity安卓平台开发,启动app并传参
using UnityEngine; using System;public class IntentReceiver : MonoBehaviour {public bool isVR1;void Start(){Debug.LogError("app1111111111111111111111111");if (isVR1){LaunchAnotherApp("com.HappyMaster.DaKongJianVR2");}else{// 检查是否有传…...

jdbcTemplate.query备忘录
jdbcTemplate.query中使用全部字符串和参数注入, 查询速度为什么差距这么大 如何正确使用JdbcTemplate参数化查询 1、使用?占位符 String sql "SELECT * FROM users WHERE name LIKE ?"; List<User> users jdbcTemplate.query(sql,new Object[…...

如何搭建Z-Blog PHP版本:详细指南
Z-Blog是一款功能强大且易于使用的博客平台,支持PHP和ASP两种环境。本文将重点介绍如何在PHP环境下搭建Z-Blog博客系统,帮助您快速上线自己的个人博客站点。 准备工作 1. 获取Z-Blog PHP版本 首先,访问Z-Blog官方网站下载最新版本的Z-Blog…...

Docker 常用命令详解
🐳 Linux 安装 Docker 及常用命令详解(适用于 Ubuntu) 📦 一、安装 Docker(Ubuntu 系统) 1. 更新系统 sudo apt update sudo apt upgrade -y2. 安装必要依赖 sudo apt install -y apt-transport-https …...
