n皇后问题的 C++ 回溯算法教学攻略
一、问题描述
n皇后问题是经典的回溯算法问题。给定一个 n×n 的棋盘,要求在棋盘上放置 n 个皇后,使得任何两个皇后之间不能互相攻击。皇后可以攻击同一行、同一列以及同一对角线上的棋子。我们需要找出所有的合法放置方案并输出方案数。
二、输入输出形式
输入形式
输入一个整数 n,表示皇后的个数和棋盘的大小(n×n)。
输出形式
输出所有的合法放置方案,每个方案占一行,皇后所在的列号用空格分隔。最后输出方案的总数。
三、样例输入输出
样例输入
4
样例输出
复制
2 4 1 3
3 1 4 2
2四、算法分析与设计
1. 回溯算法
n皇后问题适合使用回溯算法解决。回溯算法通过递归尝试所有可能的解,当发现当前路径无法得到合法解时,会回溯到上一步,尝试其他可能性。
2. 状态表示
-
board:一个一维数组,其中board[i]表示第i行皇后所在的列。 -
solutions:一个二维数组,存储所有合法的解决方案。
3. 算法步骤
-
递归放置皇后:从第一行开始,尝试将皇后放置在每一列,并检查是否与之前放置的皇后冲突。
-
冲突检查:对于每一列,检查是否与之前行的皇后在同一列或同一对角线上。
-
记录解决方案:当放置完所有行的皇后时,将当前
board状态记录为一个解决方案。 -
输出解决方案:遍历所有解决方案并输出。
五、代码实现
#include <iostream>
#include <vector>
#include <algorithm>using namespace std;int n;
vector<int> board; // 存储每一行皇后所在的列,board[i] 表示第 i 行皇后所在的列
vector<vector<int>> solutions; // 存储所有解决方案void solve(int row) {if (row == n) {solutions.push_back(board);return;}for (int col = 0; col < n; col++) {// 检查是否可以放置皇后bool valid = true;for (int i = 0; i < row; i++) {// 检查同一列和对角线是否已有皇后if (board[i] == col || abs(i - row) == abs(board[i] - col)) {valid = false;break;}}if (valid) {board[row] = col;solve(row + 1);}}
}void printSolutions() {for (const auto& solution : solutions) {for (int col : solution) {cout << col + 1 << " "; // 输出列号加 1}cout << endl;}cout << solutions.size() << endl;
}int main() {cin >> n;board.resize(n);solve(0); // 从第 0 行开始放置printSolutions();return 0;
}六、代码解析
1. 初始化
-
n:表示皇后的个数和棋盘的大小。 -
board:动态调整大小为n,初始化为一个空数组。 -
solutions:存储所有的解决方案。
2. 递归函数 solve
-
row:表示当前要放置的行。 -
当
row等于n时,表示所有行的皇后都已放置完成,将当前board加入解决方案列表。 -
对每一列进行尝试,检查是否与之前放置的皇后冲突。如果没有冲突,则将皇后放置在当前列,并递归处理下一行。
3. 冲突检查
-
检查当前列是否已经有皇后。
-
检查对角线是否已经有皇后,通过比较行差和列差的绝对值是否相等。
4. 输出解决方案
-
遍历所有解决方案,每个方案的列号加 1(因为列号从 0 开始)。
-
最后输出方案的总数。
七、复杂度分析
1. 时间复杂度
回溯算法的时间复杂度为 O(n!),因为在最坏情况下需要遍历所有可能的排列组合。
2. 空间复杂度
空间复杂度为 O(n),用于存储当前棋盘状态和解决方案。
八、总结
n皇后问题是一个经典的回溯算法问题。通过回溯算法,我们可以有效地找到所有合法的解决方案。回溯算法利用递归和冲突检查,逐步构建解决方案,并在发现路径无效时及时回溯。这种方法适用于很多组合优化问题,如排列问题、子集问题等。
希望本攻略能够帮助你理解 n皇后问题的回溯算法解法,并能够在实际问题中应用。如果有任何疑问或需要进一步的解释,请随时提问!
相关文章:

n皇后问题的 C++ 回溯算法教学攻略
一、问题描述 n皇后问题是经典的回溯算法问题。给定一个 nn 的棋盘,要求在棋盘上放置 n 个皇后,使得任何两个皇后之间不能互相攻击。皇后可以攻击同一行、同一列以及同一对角线上的棋子。我们需要找出所有的合法放置方案并输出方案数。 二、输入输出形…...

一些免费的大A数据接口库
文章目录 一、Python开源库(适合开发者)1. AkShare2. Tushare3. Baostock 二、公开API接口(适合快速调用)1. 新浪财经API2. 腾讯证券接口3. 雅虎财经API 三、第三方数据平台(含免费额度)1. 必盈数据2. 聚合…...

DeepSeek本地部署及WebUI可视化教程
前言 DeepSeek是近年来备受关注的大模型之一,支持多种推理和微调场景。很多开发者希望在本地部署DeepSeek模型,并通过WebUI进行可视化交互。本文将详细介绍如何在本地环境下部署DeepSeek,并实现WebUI可视化,包括Ollama和CherryStudio的使用方法。 一、环境准备 1. 硬件要…...
机器学习算法时间复杂度解析:为什么它如此重要?
时间复杂度的重要性 虽然scikit-learn等库让机器学习算法的实现变得异常简单(通常只需2-3行代码),但这种便利性往往导致使用者忽视两个关键方面: 算法核心原理的理解缺失 忽视算法的数据适用条件 典型算法的时间复杂度陷阱 SV…...

SSIM、PSNR、LPIPS、MUSIQ、NRQM、NIQE 六个图像质量评估指标
评价指标 1. SSIM(Structural Similarity Index) 📌 定义 结构相似性指数(Structural Similarality Index)是一种衡量两幅图像相似性的指标,考虑了亮度、对比度和结构信息的相似性,比传统的 P…...

【笔记】旧版MSYS2 环境中 Rust 升级问题及解决过程
下面是一份针对在旧版 MSYS2(安装在 D 盘)中,基于 Python 3.11 的 Poetry 虚拟环境下升级 Rust 的处理过程笔记(适用于 WIN 系统 SUNA 人工智能代理开源项目部署要求)的记录。 MSYS2 旧版环境中 Rust 升级问题及解决过…...

centos查看开启关闭防火墙状态
执行:systemctl status firewalld ,即可查看防火墙状态 防火墙的开启、关闭、禁用命令 (1)设置开机启用防火墙:systemctl enable firewalld.service (2)设置开机禁用防火墙:system…...

[论文阅读] 人工智能 | 大语言模型计划生成的新范式:基于过程挖掘的技能学习
#论文阅读# 大语言模型计划生成的新范式:基于过程挖掘的技能学习 论文信息 Skill Learning Using Process Mining for Large Language Model Plan Generation Andrei Cosmin Redis, Mohammadreza Fani Sani, Bahram Zarrin, Andrea Burattin Cite as: arXiv:2410.…...

MS31912TEA 多通道半桥驱动器 氛围灯 照明灯 示宽灯 转向灯驱动 后视镜方向调节 可替代DRV8912
MS31912TEA 多通道半桥驱动器 氛围灯 照明灯 示宽灯 转向灯驱动 后视镜方向调节 可替代DRV8912 产品简述 MS31912 是集成多种高级诊断功能的多通道半桥驱动。 MS31912 具有 12 个半桥,典型工作电压 13.5V 下,每一个半桥支持 1A 电流,典型工…...
)
软考 系统架构设计师系列知识点之杂项集萃(84)
接前一篇文章:软考 系统架构设计师系列知识点之杂项集萃(83) 第151题 在软件系统工具中,版本控制工具属于(),软件评价工具属于()。 第1空 A. 软件开发工具 B. 软件维…...

矩阵QR分解
1 orthonormal 向量与 Orthogonal 矩阵 orthonormal 向量定义为 ,任意向量 相互垂直,且模长为1; 如果将 orthonormal 向量按列组织成矩阵,矩阵为 Orthogonal 矩阵,满足如下性质: ; 当为方阵时&…...

UDP与TCP的区别是什么?
UDP和TCP是互联网通信中最常用的两种传输层协议,它们在数据传输方式、可靠性、速度和适用场景等方面存在显著差异。本文将围绕UDP与TCP的核心区别展开详细分析,包括连接方式、数据传输机制、传输效率以及各自适合的应用场景,帮助开发者和网络…...

撰写脚本,通过发布/joint_states话题改变机器人在Rviz中的关节角度
撰写脚本,通过发布/joint_states话题改变机器人在Rviz中的关节角度 提问 为我写一个改变关节base_spherical_center_high_joint角度的python脚本吧。适用于ROS2的humble 回答 下面是一个适用于 ROS 2 Humble 的 Python 脚本,它会以指定频率持续发布 …...

AOP实现Restful接口操作日志入表方案
文章目录 前言一、基础资源配置1.操作日志基本表[base_operation_log] 见附录1。2.操作日志扩展表[base_operation_log_ext] 见附录2。3.定义接口操作系统日志DTO:OptLogDTO4.定义操作日志注解类WebLog5.定义操作日志Aspect切面类SysLogAspect6.定义异步监听日志事件…...

【MATLAB去噪算法】基于CEEMDAN联合小波阈值去噪算法(第四期)
CEEMDAN联合小波阈值去噪算法相关文献 一、EMD 与 EEMD 的局限性 (1)EMD (经验模态分解) 旨在自适应地将非线性、非平稳信号分解成一系列 本征模态函数 (IMFs),这些 IMFs 从高频到低频排列。 核心问题:模态混合 (Mode Mixing) 同…...

Webhook 配置备忘
本文地址:blog.lucien.ink/archives/552 将下列代码保存为 install.sh,然后 bash install.sh。 #!/usr/bin/env bash set -e wget https://github.mirrors.lucien.ink/https://github.com/adnanh/webhook/releases/download/2.8.2/webhook-linux-amd64.…...
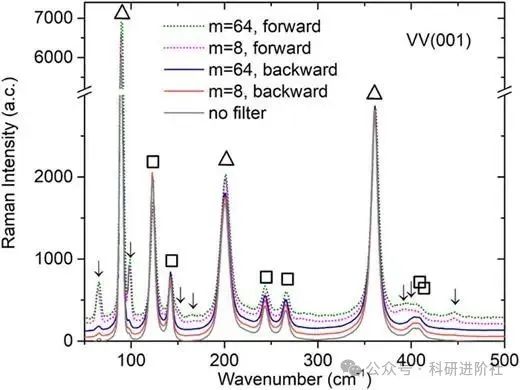
从理论崩塌到新路径:捷克科学院APL Photonics论文重构涡旋光技术边界
理论预言 vs 实验挑战 光子轨道角动量(Orbital Angular Momentum, OAM)作为光场调控的新维度,曾被理论预言可突破传统拉曼散射的对称性限制——尤其是通过涡旋光(如拉盖尔高斯光束)激发晶体中常规手段无法探测的"…...

机器学习笔记【Week7】
一、SVM的动机:大间隔分类器 1、逻辑回归回顾 假设函数为 sigmoid 函数: h θ ( x ) 1 1 e − θ T x h_\theta(x) \frac{1}{1 e^{-\theta^Tx}} hθ(x)1e−θTx1 分类依据是 h θ ( x ) ≥ 0.5 h_\theta(x) \geq 0.5 hθ(x)≥0.5 为正类&a…...

LSM Tree算法原理
LSM Tree(Log-Structured Merge Tree)是一种针对写密集型场景优化的数据结构,广泛应用于LevelDB、RocksDB等数据库引擎中。其核心原理如下: 1. 写入优化:顺序写代替随机写 内存缓冲(MemTable):写入操作首先被写入内存中的数据结构(如跳表或平衡树),…...

智能推荐系统:协同过滤与深度学习结合
智能推荐系统:协同过滤与深度学习结合 系统化学习人工智能网站(收藏):https://www.captainbed.cn/flu 文章目录 智能推荐系统:协同过滤与深度学习结合摘要引言技术原理对比1. 协同过滤算法:基于相似性的推…...

文档处理组件Aspose.Words 25.5全新发布 :六大新功能与性能深度优化
在数字化办公日益普及的今天,文档处理的效率与质量直接影响到企业的运营效率。Aspose.Words 作为业界领先的文档处理控件,其最新发布的 25.5 版本带来了六大新功能和多项性能优化,旨在为开发者和企业用户提供更强大、高效的文档处理能力。 六…...

固态继电器与驱动隔离器:电力系统的守护者
在电力系统中, 固态继电器合驱动隔离器像两位“电力守护神”,默默地确保电力设备的安全与稳定运行。它们通过高效、可靠的性能,保障了电力设备在各种环境下的正常工作。 固态继电器是电力控制中的关键组成部分,利用半导体器件来实…...

uni-app 如何实现选择和上传非图像、视频文件?
在 uni-app 中实现选择和上传非图像、视频文件,可根据不同端(App、H5、小程序)的特点,采用以下方法: 一、通用思路(多端适配优先推荐) 借助 uni.chooseFile 选择文件,再用 uni.upl…...

区块链架构深度解析:从 Genesis Block 到 Layer 2
# 区块链架构深度解析:从 Genesis Block 到 Layer 2 目录 一、Genesis Block:区块链的起点 二、Layer 0:区块链的底层网络架构 三、Layer 1:核心协议层 🚀 四、Layer 2:扩展性解决方案 五、未来展望&a…...

【数据分析】基于adonis2与pairwise.adonis2的群组差异分析教程
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍加载R包数据下载导入数据数据预处理adonis分析pairwise.adonis2分析总结系统信息介绍 本教程主要用于执行和分析基于距离矩阵的多样性和群落结构分析,特别是通过adonis2和pairwi…...

使用pdm+uv替换poetry
用了好几年poetry了,各方面都还挺满意,就是lock实在太慢; 已经试用pdmuv一段时间了,确实是快,也基本能覆盖poetry的功能。 至于为什么用pdmuv,而不是只用uv,原因很多,有兴趣的可以…...
Nginx + Tomcat负载均衡群集
目录 一、案例环境 二、部署 Tomcat(102/103) 1、准备环境 (1)关闭firewalld 防火墙 (2)安装JDK 2、安装配置 Tomcat (1)Tomcat 的安装和配置 (2)移动…...

嵌入式开发之STM32学习笔记day22
STM32F103C8T6 FLASH闪存 1 FLASH简介 STM32F1系列微控制器的FLASH存储器是一种非易失性存储器,它在微控制器中扮演着至关重要的角色。以下是对STM32F1系列FLASH存储器及其相关编程方式的扩展说明: 【FLASH存储器的组成部分】 程序存储器:这…...

分词算法BBPE详解和Qwen的应用
一、TL;DR BPE有什么问题:依旧会遇到OOV问题,并且中文、日文这些大词汇表模型容易出现训练中未出现过的字符Byte-level BPE怎么解决:与BPE一样是高频字节进行合并,但BBPE是以UTF-8编码UTF-8编码字节序列而非字符序列B…...

关于ETL的BackgroundScheduler同步方案和misfire_grace_time
如果做ETL避免脏数据,那么不可以允许同一个job有并行允许的情况,也就是说max_instance参数始终设置成1。 这时候执行ETL任务,会有以下情况。 1 任务不超时。正常执行 2 任务超时。如果下一个时间点上一次任务还没有执行完,那么…...
