一个简单的德劳内三角剖分实现
德劳内(Delaunay)三角剖分是一种经典的将点集进行三角网格化预处理的手段,在NavMesh、随机地牢生成等场景下都有应用。
具体内容百度一大堆,就不介绍了。
比较知名的算法是Bowyer-Watson算法,也就是逐点插入法。
下雨闲着没事简单实现了一下,效果如下:

思路很简单:
- 收集点集,以及点集的范围
- 初始构建一个超级三角形,将所有点包含在内,并将超级三角形加入三角形列表
- 逐个点进行插入
- 找到所有外接圆包含该插入点的三角形,标记为BadTriangle
- 从三角形列表中移除所有BadTriangle,但需要记录这些BadTriangle的边,因为之后可能需要用这些边构建新的三角形
- 将收集到的边进行去重,这里的去重指的是如果两条边的端点是同样的点,就将这两条边都删除,而不是只删除一条,实际是为了删除多个三角形之间的共享边
- 这样所有BadTriangle剩余的边就围成了一个多边形空洞,也就是所谓的空洞化
- 用这个多边形空洞的每条边跟插入点构建新的三角形,并加入三角形列表中,用于后续插入点的检查
- 超级三角形只用于辅助构建,其顶点并不是真实存在的点,因此在所有点插入完成后,需要将包含SuperTriangle顶点的三角形从列表中删除
- 构建完成
当然这只是趁午饭时间随手写的一个演示效果,没有考虑性能的问题.
代码如下:
using System.Collections.Generic;
using UnityEngine;namespace MapRandom.Delaunay
{public static class VectorExtension{public static bool Same(this Vector3 _this, Vector3 _other){return Mathf.Approximately(_this.x, _other.x) &&Mathf.Approximately(_this.y, _other.y) &&Mathf.Approximately(_this.z, _other.z);}}public class TestDelaunay : MonoBehaviour{private class Triangle{public Vector3 PointA,PointB,PointC;public List<Edge> Edges;public Vector3 Center;public float Radius;public float RadiusSqr;public Triangle(Vector3 _pointA, Vector3 _pointB, Vector3 _pointC){PointA = _pointA;PointB = _pointB;PointC = _pointC;CalcCircumcircle();CalcEdges();}/// <summary>/// 计算外接圆/// </summary>private void CalcCircumcircle(){float _ab = PointA.sqrMagnitude;float _cd = PointB.sqrMagnitude;float _ef = PointC.sqrMagnitude;float _circumX = (_ab * (PointC.y - PointB.y) + _cd * (PointA.y - PointC.y) + _ef * (PointB.y - PointA.y)) / (PointA.x * (PointC.y - PointB.y) + PointB.x * (PointA.y - PointC.y) + PointC.x * (PointB.y - PointA.y));float _circumY = (_ab * (PointC.x - PointB.x) + _cd * (PointA.x - PointC.x) + _ef * (PointB.x - PointA.x)) / (PointA.y * (PointC.x - PointB.x) + PointB.y * (PointA.x - PointC.x) + PointC.y * (PointB.x - PointA.x));Center = new Vector3(_circumX / 2, _circumY / 2);Radius = Vector3.Distance(Center, PointA);RadiusSqr = Radius * Radius;}/// <summary>/// 生成边信息/// </summary>private void CalcEdges(){Edges = new List<Edge>(3);Edges.Add(new Edge(PointA, PointB));Edges.Add(new Edge(PointB, PointC));Edges.Add(new Edge(PointC, PointA));}/// <summary>/// 检查点在外接圆内/// </summary>/// <param name="_point"></param>/// <returns></returns>public bool CheckCircumcircleContains(Vector3 _point){return Vector3.SqrMagnitude(_point - Center) < RadiusSqr;}/// <summary>/// 检查顶点包含某一点/// </summary>/// <param name="_point"></param>/// <returns></returns>public bool CheckHasVertex(Vector3 _point){return PointA.Same(_point) ||PointB.Same(_point) ||PointC.Same(_point);}}private class Edge{public Vector3 PointA,PointB;public bool IsBad;public Edge(Vector3 _pointA, Vector3 _pointB){PointA = _pointA;PointB = _pointB;IsBad = false;}/// <summary>/// 检查顶点包含某一点/// </summary>/// <param name="_point"></param>/// <returns></returns>public bool CheckHasVertex(Vector3 _point){return PointA.Same(_point) ||PointB.Same(_point);}/// <summary>/// 是否为重复边/// </summary>/// <param name="_other"></param>/// <returns></returns>public bool Same(Edge _other){return PointA.Same(_other.PointA) && PointB.Same(_other.PointB) ||PointA.Same(_other.PointB) && PointB.Same(_other.PointA);}}public Transform TestRoot;private List<Vector3> mPointList = new();private List<Triangle> mTriangleList = new();private List<Edge> mTmpEdgeList = new();private void Update(){if (null == TestRoot) return;Triangulate();}private void CollectPoints(){mPointList.Clear();for (int i = 0; i < TestRoot.childCount; i++){Transform _child = TestRoot.GetChild(i);Vector3 _point = new Vector3(_child.position.x, _child.position.y, 0);mPointList.Add(_point);}}private void Triangulate(){mTriangleList.Clear();//收集点的范围CollectPoints();float _minX = float.MaxValue, _minY = float.MaxValue;float _maxX = float.MinValue, _maxY = float.MinValue;foreach (Vector3 _point in mPointList){_minX = Mathf.Min(_minX, _point.x);_minY = Mathf.Min(_minY, _point.y);_maxX = Mathf.Max(_maxX, _point.x);_maxY = Mathf.Max(_maxY, _point.y);}//构建超级三角形float _dx = _maxX - _minX;float _dy = _maxY - _minY;float _maxDelta = Mathf.Max(_dx, _dy) * 2f;Triangle _superTriangle = new Triangle(new Vector3(_minX - 1, _minY - 1),new Vector3(_minX - 1, _maxY + _maxDelta),new Vector3(_maxX + _maxDelta, _minY - 1));mTriangleList.Add(_superTriangle);//逐点插入foreach (Vector3 _point in mPointList){//首先删除所有外接圆包含插入点的三角形//收集BadTriangle的边用于后续构建新三角形mTmpEdgeList.Clear();for (int i = mTriangleList.Count - 1; i >= 0; i--){Triangle _triangle = mTriangleList[i];if (_triangle.CheckCircumcircleContains(_point)){mTmpEdgeList.AddRange(_triangle.Edges);mTriangleList.RemoveAt(i);}}//空洞化,边查重,删除所有共享边for (int i = 0; i < mTmpEdgeList.Count; i++){Edge _edge_1 = mTmpEdgeList[i];if (_edge_1.IsBad) continue;for (int j = i + 1; j < mTmpEdgeList.Count; j++){Edge _edge_2 = mTmpEdgeList[j];if (_edge_1.Same(_edge_2)){_edge_1.IsBad = true;_edge_2.IsBad = true;}}}for (int i = mTmpEdgeList.Count - 1; i >= 0; i--){if (mTmpEdgeList[i].IsBad){mTmpEdgeList.RemoveAt(i);} }//空洞边与插入点构建新三角形foreach (Edge _edge in mTmpEdgeList){Triangle _triangle = new Triangle(_edge.PointA, _point, _edge.PointB);mTriangleList.Add(_triangle);}}//超级三角形只起辅助构建的作用,其顶点并不是真实存在的点//因此最后需要将所有超级三角形相关的三角形删除for (int i = mTriangleList.Count - 1; i >= 0 ; i--){Triangle _triangle = mTriangleList[i];if (_triangle.CheckHasVertex(_superTriangle.PointA) ||_triangle.CheckHasVertex(_superTriangle.PointB) ||_triangle.CheckHasVertex(_superTriangle.PointC)){mTriangleList.RemoveAt(i);}}}private void OnDrawGizmos(){Gizmos.color = Color.red;foreach (Triangle _triangle in mTriangleList){foreach (Edge _edge in _triangle.Edges){Gizmos.DrawLine(_edge.PointA, _edge.PointB);}}}}
}
相关文章:

一个简单的德劳内三角剖分实现
德劳内(Delaunay)三角剖分是一种经典的将点集进行三角网格化预处理的手段,在NavMesh、随机地牢生成等场景下都有应用。 具体内容百度一大堆,就不介绍了。 比较知名的算法是Bowyer-Watson算法,也就是逐点插入法。 下雨闲…...

Python入门手册:异常处理
在编程过程中,异常处理是一个非常重要的环节。它可以帮助我们处理程序运行时可能出现的错误和异常情况,确保程序的稳定性和可靠性。Python提供了强大的异常处理机制,使得我们能够优雅地处理各种异常情况。今天,就让我们一起深入学…...

C#子线程更新主线程UI及委托回调使用示例
1.声明线程方法 2.线程中传入对象 3.声明委托与使用 声明委托对象 委托作为参数传入方法 4.在线程中传入委托 5.调用传入的委托...

使用VuePress2.X构建个人知识博客,并且用个人域名部署到GitHub Pages中
使用VuePress2.X构建个人知识博客,并且用个人域名部署到GitHub Pages中 什么是VuePress VuePress 是一个以 Markdown 为中心的静态网站生成器。你可以使用 Markdown 来书写内容(如文档、博客等),然后 VuePress 会帮助你生成一个…...

手写Promise.all
前言 之前在看远方os大佬直播的时候看到有让手写的Promise.all的问题,然后心血来潮自己准备手写一个 开始 首先,我们需要明确原本js提供的Promise.all的特性 Promise.all返回的是一个Promise如果传入的数据中有一个reject即整个all返回的就是reject&…...

调试器基本原理
调试器基本原理 前言 调试器(debugger),是一种用于控制其他程序执行流程、监控和修改其他程序状态的软件工具。 调试器通过实时分析程序的执行状态,协助开发者定位代码错误、了解程序工作原理、性能调优及逆向工程等。 1. 调试器核心功能 1.1 控制程…...
2025年6月|注意力机制|面向精度与推理速度提升的YOLOv8模型结构优化研究:融合ACmix的自研改进方案
版本: 8.3.143(Ultralytics YOLOv8框架) ACmix模块原理 在目标检测任务中,小目标(如裂缝、瑕疵、零件边缘等)由于其尺寸较小、纹理信息稀疏,通常更容易受到图像中复杂背景或噪声的干扰,从而导致漏检或误检…...

JAVA开发代码小工具集合
目录 前言编号生成工具EasyExcel 工具断言工具HTTP 工具字符串 工具验证码生成工具Excel 工具Class 工具Enum 工具分页工具断言工具2IP 地址工具Map 工具 前言 这些工具都是日常开发中能用到的,前后端都有,觉得好用就拿过来了… 编号生成工具 import j…...

利用qcustomplot绘制曲线图
本文详细介绍了qcustomplot绘制曲线图的流程,一段代码一段代码运行看效果。通过阅读本文,读者可以了解到每一项怎么用代码进行配置,进而实现自己想要的图表效果。(本文只针对曲线图) 1 最简单的图形(入门&…...

【基础算法】枚举(普通枚举、二进制枚举)
文章目录 一、普通枚举1. 铺地毯(1) 解题思路(2) 代码实现 2. 回文日期(1) 解题思路思路一:暴力枚举思路二:枚举年份思路三:枚举月日 (2) 代码实现 3. 扫雷(2) 解题思路(2) 代码实现 二、二进制枚举1. 子集(1) 解题思路(2) 代码实现 2. 费解的…...

智能对联网页小程序的仓颉之旅
#传统楹联遇上AI智能体:我的Cangjie Magic开发纪实 引言:一场跨越千年的数字对话 "云对雨,雪对风,晚照对晴空"。昨天晚上星空璀璨,当我用仓颉语言写下第一个智能对联网页小程序的Agent DSL代码时࿰…...

Go字符串切片操作详解:str1[:index]
在Go语言中,return str1[:index] 是一个字符串切片操作,它截取字符串的一部分。让我们深入解析这个操作的含义和原理: 基本语法和含义 str1:原始字符串[:index]:切片操作符str1[:index]: 起始…...
 完全指南)
JavaScript 本地存储 (localStorage) 完全指南
文章目录 JavaScript 本地存储 (localStorage) 完全指南 🔐一、什么是 localStorage?💡二、如何使用 localStorage?🔧1. 存储数据2. 读取数据3. 删除数据4. 清空所有数据 三、存储对象和数组的技巧 🎨1. 存…...

从golang的sync.pool到linux的slab分配器
最近学习golang的时候,看到golang并发编程中有一个sync.pool,即对象池,猛地一看这不跟linux的slab分配器类似嘛,赶紧学习记录下 这里先总结下设计sync.pool和slab的目的 sync.pool 为了缓解特定类型的对象频繁创建和销毁&#x…...

Python分形几何可视化—— 复数迭代、L系统与生物分形模拟
Python分形几何可视化—— 复数迭代、L系统与生物分形模拟 本节将深入探索分形几何的奇妙世界,实现Mandelbrot集生成器和L系统分形树工具,并通过肺部血管分形案例展示分形在医学领域的应用。我们将使用Python的NumPy进行高效计算,结合Matplo…...

【超详细】英伟达Jetson Orin NX-YOLOv8配置与TensorRT测试
文章主要内容如下: 1、基础运行环境配置 2、Torch-GPU安装 3、ultralytics环境配置 4、Onnx及TensorRT导出详解 5、YOLOv8推理耗时分析 基础库版本:jetpack5.1.3, torch-gpu2.1.0, torchvision0.16.0, ultralytics8.3.146 设备的软件开发包基础信息 需…...

Go语言学习-->项目中引用第三方库方式
Go语言学习–>项目中引用第三方库方式 1 执行 go mod tidy 分析引入的依赖有没有正常放在go.mod里面 找到依赖的包会自动下载到本地 并添加在go.mod里面 执行结果: 2 执行go get XXXX(库的名字)...

Vue Fragment vs React Fragment
文章目录 前言🧩 一、概念对比:Vue Fragment vs React Fragment📦 二、使用示例对比✅ Vue 3 中使用 Fragment✅ React 中使用 Fragment 🔍 三、差异解析1. **使用方式**2. **传递属性(如 key)**3. **插槽系…...
)
【LRU】 (最近最少使用)
LRU (最近最少使用) 文章目录 LRU (最近最少使用)一、LRU是什么?二、实现1.常规算法2.双栈更替总结 一、LRU是什么? LRU(Least Recently Used)是一种常见的缓存淘汰策略,核心思想是 “淘汰最长时间未被使用的缓存数据…...

每日Prompt:云朵猫
提示词 仰视,城镇的天空,一片形似猫咪的云朵,用黑色的简笔画,勾勒出猫咪的形状,可爱,俏皮,极简...

AI浪潮下的IT行业:威胁、转变与共生之道
目录 前言1 AI在IT行业的具体应用场景1.1 软件开发中的AI助手1.2 运维与监控的智能化1.3 测试自动化与质量保障1.4 安全防护中的智能威胁识别 2 AI对IT从业者的实际影响2.1 工作内容的结构性变化2.2 技能结构的再平衡 3 IT从业者不可替代的能力与价值3.1 复杂系统的架构与抽象能…...

基于功能基团的3D分子生成扩散模型 - D3FG 评测
D3FG 是一个在口袋中基于功能团的3D分子生成扩散模型。与通常分子生成模型直接生成分子坐标和原子类型不同,D3FG 将分子分解为两类组成部分:官能团和连接体,然后使用扩散生成模型学习这些组成部分的类型和几何分布。 一、背景介绍 D3FG 来源…...

Python Cookbook-7.12 在 SQLite 中储存 BLOB
任务 想将 BLOB 存入一个 SQLite 数据库, 解决方案 Python的 PySQLite 扩展提供了 sqlite.encode 函数,它可帮助你在 SOLite 数据库中插入二进制串。可以基于这个函数编写一个小巧的适配器类: import sqlite,cPickle class Blob(object):自动转换二进制串def __init__(self…...

蓝耘服务器与DeepSeek的结合:引领智能化时代的新突破
🌟 嗨,我是Lethehong!🌟 🌍 立志在坚不欲说,成功在久不在速🌍 🚀 欢迎关注:👍点赞⬆️留言收藏🚀 🍀欢迎使用:小智初学…...

无人机光纤FC接口模块技术分析
运行方式 1. 信号转换:在遥控器端,模块接收来自遥控器主控板的电信号。 2.电光转换:模块内部的激光发射器将电信号转换成特定波长的光信号。 3.光纤传输:光信号通过光纤跳线传输。光纤利用全内反射原理将光信号约束在纤芯内进行…...
)
【LeetCode】3170. 删除星号以后字典序最小的字符串(贪心 | 优先队列)
LeetCode 3170. 删除星号以后字典序最小的字符串(中等) 题目描述解题思路java代码 题目描述 题目链接:3170. 删除星号以后字典序最小的字符串 给你一个字符串 s 。它可能包含任意数量的 * 字符。你的任务是删除所有的 * 字符。 当字符串还…...

Oracle 用户名大小写控制
Oracle 用户名大小写控制 在 Oracle 数据库中,用户名的默认大小写行为和精确控制方法如下: 一 默认用户名大小写行为 不引用的用户名:自动转换为大写 CREATE USER white IDENTIFIED BY oracle123; -- 实际创建的用户名是 "WHITE"…...
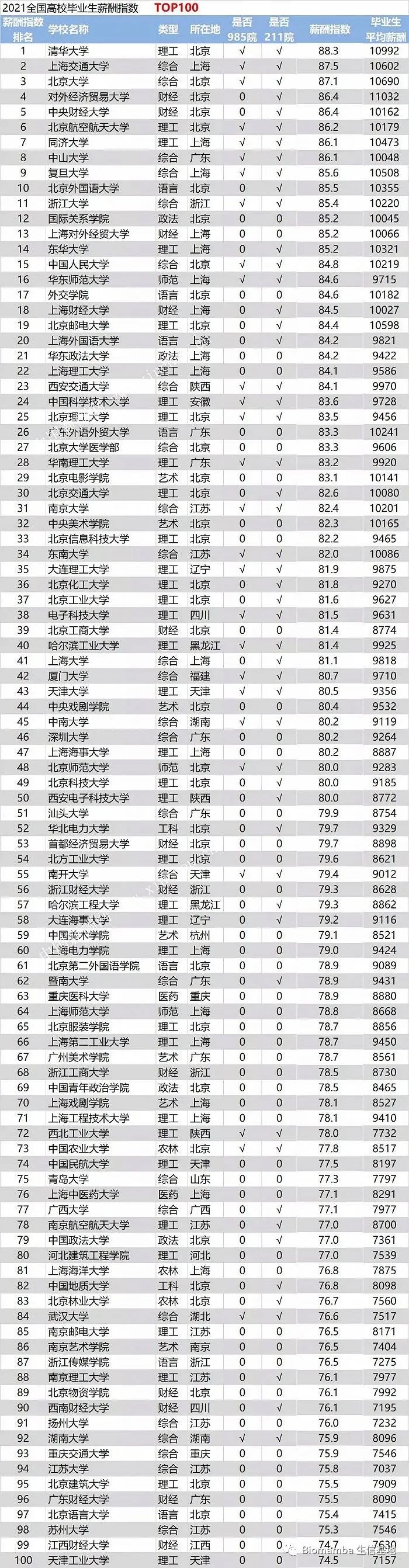
作为过来人,浅谈一下高考、考研、读博
写在前面 由于本人正在读博,标题中的三个阶段都经历过或正在经历,本意是闲聊,也算是给将要经历的读者们做个参考、排雷。本文写于2022年,时效性略有落后,不过逻辑上还是值得大家参考,若所述存在偏颇&#…...

立志成为一名优秀测试开发工程师(第十一天)—Postman动态参数/变量、文件上传、断言策略、批量执行及CSV/JSON数据驱动测试
目录 一、Postman接口关联与正则表达式应用 1.正则表达式解析 2.提取鉴权码。 二、Postman内置动态参数以及自定义动态参数 1.常见内置动态参数: 2.自定义动态参数: 3.“编辑”接口练习 三、图片上传 1.文件的上传 2.上传后内容的验证 四、po…...

Global Security Market知识点总结:主经纪商业务
在全球证券市场的复杂体系中,主经纪商业务(Prime Brokerage)占据着独特且关键的位置。这一业务为大型机构投资者提供了一系列至关重要的服务,极大地影响着金融市场的运作与发展。 一、主经纪商业务的定义 主经纪商业务是投资银行…...
