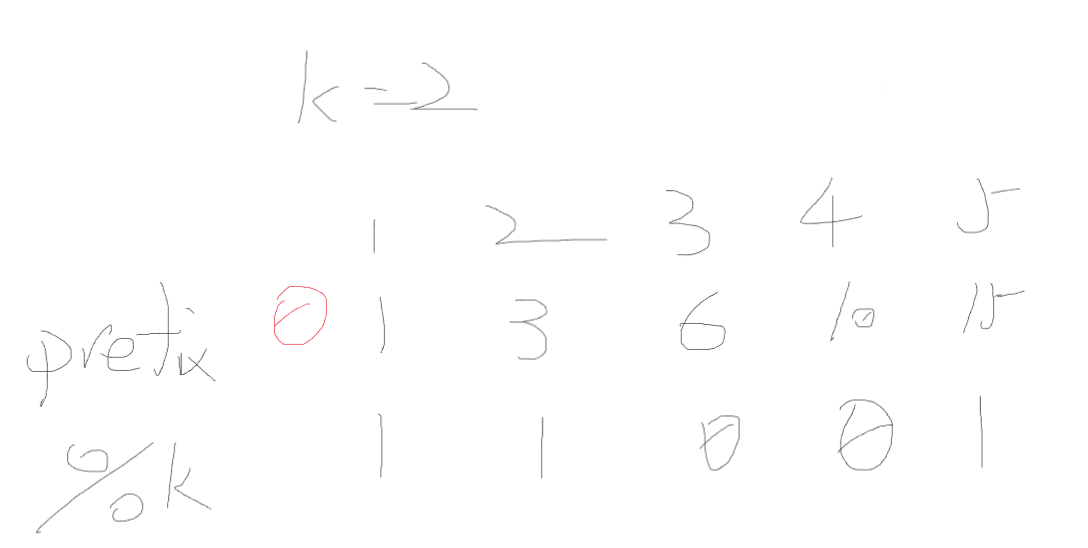算法(蓝桥杯学习C/C++版)
up:
溶金落梧桐
溶金落梧桐的个人空间-溶金落梧桐个人主页-哔哩哔哩视频
蓝桥杯三十天冲刺系列
BV18eQkY3EtP
网站:
OI Wiki
OI Wiki - OI Wiki
注意
比赛时,devc++勾选c++11(必看)
必须勾选c++11一共有两个方法,任用一个就可以了。(方法一有两个c++11可以选,好像都可以)
如果不勾选,map、to_string等不能使用,无法编译
蓝桥杯用的是c++11,所以C++17自带gcd函数或GCC拓展的__gcd函数不能用
- 方法一:

- 方法二

c++大概一秒跑10⁸的数据
10^8,大约是2^26次
对于子集枚举的算法中,O(n)=2^n
int大约2.1*10^9
long long大约9.2*10^18
c++除法 / 是向0取整(对于正数就是向下取整)
return退出函数
return 可以用来退出函数,如果是嵌套的循环,想要直接退出,要在每一层循环都break
可以用return
一般在main函数中调用solve()函数,在solve()函数中写解题逻辑
void solve(){for(){for(){for(){//这里使用return,直接退出了循环//如果用break,在这里要使用三次,每一层都写一遍return;}}}
}int main(){solve();return 0;
}变量int _=1;
首先使用
_作为变量名是符合语法规则的使用 _ 来作为这种控制循环次数的变量。一种竞赛时的默认写法,有一定的通用性
#include <bits/stdc++.h>
using namespace std;void solve(){}int main() {//使用下划线int _=1;while(_--)solve();return 0;
}万能头
定义万能头,不需要敲所有的头文件了,因为都包含了
缺点:影响编译速度,和运行速度没有关系,所以比赛可以用
#include <bits/stdc++.h>关闭缓冲流
提高运行效率
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);return 0;
}endl比'\n'慢
直接这样换,即打的轻松,又用了'\n'
#define endl '\n'#define int long long
如果代码中混合使用 int 和 long long,可能导致隐式类型转换错误。统一使用 long long 可以避免这类问题
int main必须改为signed main
#include <bits/stdc++.h>
using namespace std;
#define int long longsigned main(){return 0;
}数组开大一点点,定义到全局
对于题目给出的数组,自己定义的时候,开大一点点(数字随便,多10个甚至9个都行),为了防止数组越界
数组定义到全局里,不要定义在main中,c++中,如果把数组定义到main函数中,main函数是栈空间,空间比较小,一定义可能会把栈爆了
#include <bits/stdc++.h>
using namespace std;//如果题目要求a数组最大是1000,开大一点点
//定义到全局,不要定义在main函数中
const int NN=1010;
int a[NN];int main(){return 0;
}记忆化搜索的dp,如果是多测(多组测试数据),不要写memset
memset的复杂度是数组的空间复杂度,如果是多组测试数据,用for循环手动把dp初始化成-1
main函数外声明的函数顺序影响调用
同理全部变量的声明也要放在最上面
#include <bits/stdc++.h>
using namespace std;//可以在最上面使用函数声明({}前的,带个分号),这么就无关定义顺序了
void f2();//这个f3不可以使用,因为f3之中有f2,f2还没有定义,f3不知道调用什么
void f3(){f2();
}void f2(){}//这个f1可以使用,因为f2已经定义了,f1在调用f2的时候知道是什么函数
void f1(){f2();
}int main() {return 0;
}由数据范围反推算法复杂度以及算法内容
枚举

题目
蓝桥杯第15届-好数
日期模拟
得到星期:
在最外层的year循环外面,int week=x;//x是第一天的星期
在第三层day循环里面,week=week%7
题目
蓝桥杯 2024 省 A-艺术与篮球

#include <bits/stdc++.h>
using namespace std;int ans=0;
int bh[]={13,1,2,3,5,4,4,2,2,2};
int months[]={-1,31,28,31,30,31,30,31,31,30,31,30,31};bool leap(int year){return (year%400==0)||((year%4==0)&&(year%100!=0));
}void solve(){for(int year=2000;year<=2024;year++){//闰年特判months[2] = leap(year) ? 29 : 28;for(int month=1;month<=12;month++){for(int day=1;day<=months[month];day++){int y1,y2,y3,y4,m1,m2,d1,d2;y1=year/1000;y2=year/100%10;y3=year/10%10;y4=year%10;m1=month/10%10;m2=month%10;d1=day/10%10;d2=day%10;int sum=bh[y1]+bh[y2]+bh[y3]+bh[y4]+bh[m1]+bh[m2]+bh[d1]+bh[d2];if(sum>50)ans++;if(year==2024&&month==4&&day==13)return;}}}
}int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();cout<<ans;return 0;
}进制转换

将字符转换成数字
如果是数字字符,这个字符 c - '0' 就能直接转换为对应的数字值
如果是字母字符,判断条件字符 c >= 'A',c - 'A' + 10 就能转换为对应的数字值(16进制,A表示10,所以字母对应数字是从10开始的)
提升位权(把字符变数字一定要提升位权)
之前累加的结果 ans 乘以进制 k,这相当于把之前的结果左移一位(也就是提升一位位权)
K进制转十进制

c是char类型,是字符。如字符'1'是按照ascii存,数字字符-'0'得到int类型的数字
int calc(char c) {// 如果字符是字母(即大于 '9')转换为对应的数字值(A=10, B=11, ...)if(c >= 'A') return c - 'A'+10;// 如果是数字字符,直接转换为对应的数字值return c - '0';
}int change(int k, string s) {int ans = 0;for(int i = 0; i < s.size(); i++) {ans = ans * k + calc(s[i]); // 基于进制 k 进行累加}return ans; // 返回转换后的十进制数
}十进制转K进制(短除法)
关键:十进制x%=k(得到k进制的当前位),然后x/=k(更新x)

string change(int x, int k) {string ans; // 初始化空字符串,用于存储转换结果while (x) {int tmp = x % k; // 计算 x 对 k 取余,得到当前位的值// 如果余数小于等于9,直接将其转换为字符并追加到结果字符串// 因为是字符串和字符,所以+代表拼接if (tmp <= 9) {// '0' + tmp 转为对应数字字符的ASCII码//因为tmp是int,'0'强转成int,所以得到得是ASCII码中的整数//需要强转成char才能获得真正对应的数字字符ans = ans + (char)(tmp + '0'); } else {// 如果余数大于9,表示需要用字母 A, B, C...表示(例如10为A,11为B等)// tmp - 10 + 'A' 转为对应字母字符的ASCII码ans = ans + (char)( tmp - 10 + 'A' ); }x /= k; // 更新 x,x 除以 k}// 将结果字符串反转并返回,返回的字符串为转换后的进制表示reverse(ans.begin(), ans.end()); // reverse反转字符串(注意:没有返回值)//返回反转的字符串return ans;
}题目
穿越时空之门

#include <bits/stdc++.h>
using namespace std;
int cnt=0;//求k进制各数位之和
int calc(int n,int k){int sum=0;while(n){sum=sum+n%k;n/=k;}return sum;
}void solve(){for(int i=1;i<=2024;i++){if(calc(i,2)==calc(i,4))cnt++;}
}int main(){solve();cout<<cnt;return 0;
}一维前缀和
一维前缀和,即一个数列中,某个数的前n项和=前n-1项的和+这个数
计算前缀和时,索引从1开始,让prefix[0]用默认的0
区间和查询
sum[ l,r ]区间和,即 l~r 之间的和,即 r 的前缀和减去 l 前面一项的前缀和
不会看,直接无脑把区间和sum设置成long long类型后,就不管了
在题目求和中,运用了一维前缀和的思维,出现了int*int的情况,强转成long long防止溢出
sum=sum+(long long)a[i]*(prefix[n]-prefix[i]);
前缀和求差分得到原数组
差分,就是后一项减去前一项的行为
a[ i ] = prefix[ i ] - prefix[ i-1 ] // 对于 i > 0

题目
一维前缀和
#include <bits/stdc++.h>
using namespace std;const int NN=1e5+10;
int n,q;
int a[NN];
int prefix[NN];int main() {cin>>n>>q;for(int i=1;i<=n;i++){cin>>a[i];prefix[i]=prefix[i-1]+a[i];}int sum=0;for(int i=0;i<q;i++){int l,r;cin>>l>>r;int sum=prefix[r]-prefix[l-1];cout<<sum<<endl;}return 0;
}求和(强转成long long类型,防止溢出)

思路:
#include <bits/stdc++.h>
using namespace std;const int NN=2e5+10;
int a[NN];
int b[NN];
int n;int main()
{cin>>n;for(int i=1;i<=n;i++){cin>>a[i];b[i]=b[i-1]+a[i];}long long sum=0;for(int i=1;i<n;i++){//i=1时,是a2+a3+...+an,第一个元素索引是i+1,b[i+1-1]//这里int*int会溢出,强转成long longsum=sum+(long long)a[i]*(b[n]-b[i]);}cout<<sum;return 0;
}一维差分(解决区间修改问题)
对差分数组求前缀和得到原数组(个人理解:求第i项原数组=前一项(i-1)原数组+位置i-1到i的变化率(diff[ i ]))
a[ i ] = a[ i-1 ] + diff[ i ]
a[i-1]:表示前一个位置(i-1)的原始值
diff[i]:表示从位置i-1到位置i的"变化量"或"增量"(即变化率)

差分数组,即这一项与前一项之差
对于数组[ 2,3,7,4,5,1 ],一维差分[ 2,1,4,-3,1,-4 ]
一维差分的前缀和就是原数组(可以看成积分求面积)
快速区间修改
在区间[ l,r ]修改
b[l] += d,相当于对后面所有的项都形成了“连坐”的反应,要求在[ l,r ]区间修改,即希望这个“连坐”只在这个区间有效,所以 b[r+1] -=d 来消除“连坐”影响(差分,就是变化率,对差分的修改,就是直接修改了变化率,而不是修改原数组)
对于数组[ 2,3,7,4,5,1 ],一维差分[ 2,1,4,-3,1,-4],希望[ 3,7,4 ]这个序列全部加上3,对应公式b[2]+=3,b[5]-=3
先看b[2]+=3,后面全部被影响了
再看b[5]-=3
判定序列中是否全部数字相同
已知:差分数组求前缀和就是原数组
当差分数组除第一项以外的所有项数均为0时,原数组一定所有数字相同(因为前缀和一致)
让某一项-1,再让某一项+1(相当于对原序列中的某一个连续的区间全部-1)
最后再让某一项-1
如:
1 2 -1
第二项-1,第三项+1:1 1 0
第二项-1,让不参与计算的n+1项+1: 1 0 0 [+1]
无解的情况
1 2 -3
无论如何 -3不能变成0,因为只能让某一项-1后,让某一项+1,第一项是不参与的,其他的正数和,比-3小,所以不够
在正数和<负数和时,无解
让原数组变成相同的数字
就是让一维差分数组的的b[1]有值,而且所有都是0
i==1时的特判
让一维差分方程b[i](i>1)变成0的操作数,就是所有一维差分数组中所有的正数的和
b[1] 作为差分数组的第一个元素,和其他 b[i](i > 1) 一样,都是差分数组整体的一部分。在处理差分数组时,为了保证处理逻辑的一致性和完整性,把b[1]的值也加上,先把它视做和其他b[i]一样要归0的数
因为本题要求原数组最后全为1,即要b[1]=1,所以在代表操作数的ans+b[1]只有-1,表示留下数字,不要操作,比如这里希望b[1]=1,就要-1,表示操作时,要留下一个数字不操作,它就被保留下来了,最后就是b[1]=1。如果是-1,表示留下两个数字不操作,最后就是b[1]=2
i==1时的特判,按情况而定
long long ans=0;for(int i=1;i<=n;i++){//i=1时的特判if(i==1){ans=ans+diff[1]-1;}else{if(b[i]>0)ans=ans+diff[i];}}题目
一维差分

#include <bits/stdc++.h>
using namespace std;const int NN=2e5+10;
int n,m;
int a[NN],b[NN];int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];b[i]=a[i]-a[i-1];}for(int i=1;i<=m;i++){int l,r,d;cin>>l>>r>>d;b[l]+=d;b[r+1]-=d;}for(int i=1;i<=n;i++){b[i]=b[i-1]+b[i];cout<<b[i]<<" ";}return 0;
}小蓝的操作数

#include <bits/stdc++.h>
using namespace std;const int N=1e5+10;
int a[N],diff[N];
int n;int main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];diff[i]=diff[i]-diff[i-1];}long long ans=0;for(int i=1;i<=n;i++){//i=1时的特判if(i==1){ans=ans+diff[1]-1;}else{if(b[i]>0)ans=ans+diff[i];}}cout<<ans;return 0;
}二维前缀和
二维前缀和
prefix是前缀和数组,a是原序列(即这个格子的值)
prefix[ i ][ j ] 表示从 a[ 1 ][ 1 ] 到 a[ i ][ j ] 的子矩阵中所有元素的和
构造二维前缀和数组公式:
prefix[ i ][ j ]=prefix[ i-1 ][ j ]+prefix[ i ][ j-1 ]-prefix[ i-1 ][ j-1 ]+a[ i ][ j ];
(s[ i ][ j ]=a[ i ][ j ]+s[ i-1 ][ j ]+s[ i ][ j-1 ]-s[ i-1 ][ j-1 ],两个是一样的,用prefix名字清晰,图中忽视S,只看坐标就行)
通过二维前缀和数组,求解某个子矩阵数组的值:
求解(x1,y1)到(x2,y2)
prefix[ x2 ][ y2 ]-prefix[ x1-1 ][ y2 ]-prefix[ x2 ][ y1-1 ]+prefix[ x1-1 ][ y1-1 ]
前缀和求差分得到原数组(差分,就是前一项减去后一项)
a[ i ][ j ] =prefix[ i ][ j ]-prefix[ i−1 ][ j ]-prefix[ i ][ j−1 ]+prefix[ i−1 ] [ j−1 ]
二维前缀和

#include <bits/stdc++.h>
using namespace std;const int NN=1010;
int a[NN][NN],s[NN][NN];
int n,m,q;int main(){cin>>n>>m>>q;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];//构建二维前缀和数组prefix[i][j]=prefix[i-1][j]+prefix[i][j-1]-prefix[i-1][j-1]+a[i][j];}}for(int i=1;i<=q;i++){int x1,y1,x2,y2;cin>>x1>>y1>>x2>>y2;cout<<prefix[x2][y2]-prefix[x1-1][y2]-prefix[x2][y1-1]+prefix[x1-1][y1-1]<<endl;}return 0;
}二维差分(子矩阵修改问题)

用差分数组进行区间更新:
假设我们要对子矩阵 (x1,y1) 到 (x2,y2) 的所有元素加上 d,可以转化为对差分数组 diff[][] 的 4 个单点操作
这个一个二维的差分
希望对(x1,y1)到(x2,y2)这一块就加上d,对diff[x1][y1]+d之后,从(x1,y1)开始,一直到最右下角(某个点(n,m))都会加上d
这时候,我们要消除不需要的加d操作
diff[ x1 ] [y1 ] += d(标记左上角,表示从 (x1,y1) 开始的所有区域都 +d,一直加到了右下角,)
diff[ x2+1 ][ y1 ] -= d(标记左下角,表示从 (x2+1,y1) 开始的所有区域撤销 +d)
diff[ x1 ] [ y2+1 ] -= d(标记右上角,表示从 (x1,y2+1) 开始的所有区域撤销 +d)
diff[ x2+1 ][ y2+1 ] += d(右下角,多减的补回来)
二维差分求前缀和,得到原数组(原数组=前一项数组+变化率diff):
a[ i ][ j ]=a[ i−1 ][ j ]+a[ i ][ j−1 ]−a[ i−1 ][ j−1 ]+diff[ i ][ j ]
构造差分数组(后一项减前一项):
diff[ i ][ j ]=a[ i ][ j ]-a[ i−1 ][ j ]-a[ i ][ j−1 ]+a[ i−1 ][ j−1 ]
(对于差分的理解就是前一项减去后一项,但是在二维数组中,二维的“后一项”是从左上角到这个点( i,j )的,而“前一项”也是同理,对于二维,要减去这个点( i,j )的左侧( i,j-1 )和上侧(i-1,j),再补上多减的( i-1,j-1 ))
题目
二维差分

#include <bits/stdc++.h>
using namespace std;const int NN=1010;
int a[NN][NN];
int diff[NN][NN];
int n,m,q;
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m>>q;for(int i=1; i<=n; i++) {for(int j=1; j<=m; j++) {cin>>a[i][j];diff[ i ][ j ]=a[ i ][ j ]-a[ i-1 ][ j ]-a[ i ][ j-1 ]+a[ i-1 ][ j-1 ];}}//查询while(q--) {int x1,y1,x2,y2,d;cin>>x1>>y1>>x2>>y2>>d;diff[x1][y1]+=d;diff[ x2+1 ][ y1 ] -= d;diff[ x1 ] [y2+1 ] -= d;diff[ x2+1 ][ y2+1 ] += d;}//求前缀和for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {a[i][j] = diff[i][j] + a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];cout << a[i][j] << " ";}cout << endl;}return 0;
}棋盘

#include <bits/stdc++.h>
using namespace std;const int NN=2010;
int a[NN][NN],diff[NN][NN];
int n,m;int main()
{cin>>n>>m;while(m--){int x1,y1,x2,y2;cin>>x1>>y1>>x2>>y2;//原数组是0,差分数组也是0,不用在构建差分数组了,直接操作diff[x1][y1]+=1;diff[x2+1][y1]-=1;diff[x1][y2+1]-=1;diff[x2+1][y2+1]+=1;}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+diff[i][j];//反转奇数次就是1,反转偶数次就是0cout<<a[i][j]%2;}cout<<endl;}return 0;
}二分
左程云-二分搜索
BV1bX4y177uT
序列二分
"大于等于"和"等于的最左边"(即查找第一个满足条件的元素,即求最小,舍弃右边)可以使用同一个模板
"小于等于"和"等于的最右边"(即查找最后一个满足条件的元素,即求最大,舍弃左边)可以使用同一个模板
输出有序数组中等于 x 的最左边的数的下标
因为求的是最左边的x,所以把右边抛弃,a[mid] 在 x 右边,包含了mid这个位置(a[mid]>=x),右边不要(r=mid)(因为包含了mid这个位置,即a[mid]有等于x的可能,不能把mid这个位置舍去)
a[mid] 在 x 左边的可能,不包含mid这个位置(a[mid]<x),左边不要(l=mid+1)(因为不包括mid这个位置,a[mid]不等于x,
它一定不是要求的位置,把包含mid的左边部分舍去,由于舍弃的是左边,即要加1,在更右边的位置从算把mid一起舍弃)
while(l < r) {int mid = l + r >> 1;if(a[mid] >= x) r = mid;else l = mid + 1;}if(a[l] == x) cout << l << endl;输出有序数组中等于 x 的最右边的数的下标(求最大,把左边抛弃)
思路和前面一样
只是把包含mid的右边部分舍去,由于舍弃的是右边,即要减1,在更左边的位置才算把mid一起舍弃
int mid=l+r+1>>1,记住和 mid-1 绑定
while(l < r) {int mid = l + r + 1 >> 1;if(a[mid] <= x) l = mid;else r = mid - 1;}if(a[l] == x) cout << l << endl;查找第一个大于x的元素(不含等于)
对于a[mid]==x的情况
在大于等于x,和小于等于x的要求中,要把a[mid]保留
但在大于x或者小于x的要求中,要把a[mid]跳过
while(l < r) {int mid = l + r >> 1;if(a[mid] > x) { // 仅大于,不含等于r = mid;} else {l = mid + 1; // 包括等于的情况都跳过}
}查找最后一个小于x的元素(不含等于)
while(l < r) {int mid = l + r + 1 >> 1;if(a[mid] < x) { // 仅小于,不含等于l = mid;} else {r = mid - 1; // 包括等于的情况都跳过}
}upper_bound()和low_bound()函数
upper_bound()和lower_bound(),stl中的二分查找函数,返回的是一个指针/迭代器
upper_bound(first,last,value):
在范围 [first,last) 内查找第一个大于value的元素位置(结果减1得到了最后一个小于等于value的位置,注意题目)lower_bound(first,last,value):
在范围 [first,last) 内查找第一个不小于(大于等于)value的元素位置(用value+1来达成和upper_bound一样,找到大于value的元素)
对于引用:比如&a[3],想要获得引用的值,只需要让引用减去第0项的引用,在这里就是&a[3]-&a[0]
对于数组,如int a[N],a本身就是第0项的引用,所以也可以写成&a[3]-a,让得到的是元素在数组中的索引(从0开始)
题目
整数查找(模板题)
蓝桥账户中心
最大通过数

#include<bits/stdc++.h>
using namespace std;typedef long long ll;
const int N=2e5+5;
ll a[N],b[N];int main() {ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int n,m,k;cin>>n>>m>>k;for(int i=1; i<=n; i++) {cin>>a[i];//原地做前缀和a[i]=a[i-1]+a[i];}for(int i=1; i<=m; i++) {cin>>b[i];//原地做前缀和b[i]=b[i-1]+b[i];}int ans=0;//因为关卡或许连第一关都没过,所以索引从0开始for(int i=0; i<=n; i++) {//第一关水晶用完了,breakif(a[i]>k)break;//第一关剩下的水晶ll rest=k-a[i];//upper_bound找到首个大于value的元素的迭代器,得到结果-1,获得最后一个小于等于value的迭代器,减去数组得到元素值//b+m+1,+1确保搜索到最后一个元素,因为upper_bound和lower_bound都是[first,last)int j=upper_bound(b,b+m+1,rest)-1-b;ans=max(i+j,ans);}cout<<ans;return 0;
}暴力
答案二分

左程云
BV1Mh4y1P7qE

阶乘后的0(额外)
阶乘尾数的0,是由1到n中,因子10的数量决定,每有一个10,新增一个0
而10=2*5
含有2的因子,每两个出现一次,含有5的因子,每五个出现一次
所以因子5的个数一定小于因子2的个数
所以求1到n中因子5的个数就是答案
含有5的因子,每五次出现一次(5,10,15……)
含有5的平方的因子,每25(5的平方)次,出现一次(25,50……)
含有5的三次方的因子,每125(5^3)次,出现一次(125……)
依此类推
int countTrailingZeros(int n) {int cnt = 0;while (n) {cnt += n/5;//除以5,方便进行迭代n /= 5;}return cnt; }
题目
二分答案
解析
随着枚举的最小值变大,消耗的x越来越多,即x剩余的越来越少
对于枚举的 i,上限在本题中是10^6+10^13(操作数k+a的最大值),这里直接用1e14

进行二分,对中间的m进行左边的操作,如果不对,就不要了
然后就是普通二分的思路了

代码
暴力(过不了,了解一下思路)
#include<bits/stdc++.h>
using namespace std;typedef long long ll;
const int NN=1e5+10;
ll k;
int n;
int a[NN];void solve(){cin>>n>>k;for(int i=1;i<=n;i++){cin>>a[i];}//用来枚举数组中最小值,即通过最多k次操作使得数组中的所有元素都至少为i/*输入的a上限是1e6,操作次数k上限是1e13,当序列中只有一个数是1e6k次操作后这个数最大的可能性是这个数最大可能性变成1e13+1e6*/for(int i=1;i<=1e13+1e6;i++){/*用ll cnt=0 //cnt表示操作数*///把操作数赋值给xll x=k;//用来枚举序列中每一个数for(int j=1;j<=n;j++){//如果这个数小于最小值,更新操作数if(a[j]<i){k=k-(i-a[j]);/*cnt+=i-a[j] //把每次需要的操作数加上,也可以这样想,不过对于答案二分的「给定条件」和「问题答案」之间的关系不明确*/;}//至少要把数组中每一个变成i,操作次数不够,就不能把每一个数变成i了//i-1 是最后一个满足条件的 i(因为 i-1 时 k 还没耗尽)/*if(cnt>k)*/if(x<0){cout<<i-1;return;}}}
}int main() {ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int t=1;while(t--){solve();}return 0;
}答案二分
#include<bits/stdc++.h>
using namespace std;typedef long long ll;
const int NN=1e5+10;
ll k;
int n;
int a[NN];bool check(ll m){ll x=k;for(int j=1;j<=n;j++){if(a[j]<m){//得到剩余操作数x=x-(m-a[j]);}if(x<0){return false;}}return true;
}void solve(){cin>>n>>k;for(int i=1;i<=n;i++){cin>>a[i];}//r表示上限,应该是a的最大值+k的最大值,1e6+1e13,这里用1e14方便写ll l=1,r=1e14;while(l<r){ll mid=l+r+1>>1;if(check(mid)) l=mid;else r=mid-1;}cout<<l;
}int main() {ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int t=1;while(t--){solve();}return 0;
}代码解析
贪心思想:
对于每个元素,严格按需分配操作次数:只提升不足m的部分。
不浪费操作次数在已经≥m的元素上
(m - a[ j ]) 的含义:
如果当前元素 a[ j ] 小于 m,则需要将它从 a[ j ] 提升到 m。需要操作的次数 = 两者的差值 = m - a[ j ]
(例如:a[ j ]=2,m=5 → 需要 5-2=3 次操作)
if(check(mid)) l=mid:
这里true的情况是所有元素>=mid的情况,所以包含了mid
求阶乘

代码(90%)
#include <bits/stdc++.h>
using namespace std;
#define int long long int countZero(int n) {int cnt = 0;while (n){cnt += n / 5;n /= 5;}return cnt;
}int K;
signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);cin >> K;int l = 0, r = 1e18;while (l < r) {int mid = l + r >> 1;if (countZero(mid) >= K) r = mid;else l = mid + 1;}if (countZero(l) == K) cout << l;else cout << -1;return 0;
}数列分段

题目解析
数组4 2 4 5 1,要求分成三段
我们假设,每一段的最大值是1
放入第一个数组4,就直接爆了,不行
依次类推,枚举的最大值,从1开始到3,都会爆
直接看5
数组4 2 4 5 1,放了三个数字,5放不进,所以枚举的最大值5不行
枚举每一段的最大值是6
首先放入4,发现可以放后面的数字2,就继续放,第一段放了4和2
之后数组都能放进去
所以6是最先符合的
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;const int NN=1e5+10;
int a[NN];
int N,M;bool check(ll mid){//每一段内的和,用来判断分段ll sum=0;//段数,一开始默认段数就是1了int cnt=1;for(int i=1;i<=N;i++){//这个数大于要求的最大值,怎么也放不进,直接falseif(a[i]>mid)return false;if(sum+a[i]<=mid){sum+=a[i];}else{//当这一段爆了之后,增加一段,里面的容量重新开始算cnt++;sum=a[i];}}return cnt<=M;
}void solve(){cin>>N>>M;for(int i=1;i<=N;i++){cin>>a[i];}ll l=1,r=(ll)(1e13);while(l<r){ll mid=r+l>>1;if(check(mid))r=mid;else l=mid+1;}cout<<l;
}int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;while(t--)solve();return 0;
}代码解析
当枚举的最小值的二分后,mid所代表的cnt>m了,所以mid不行,二分逻辑上的mid的左边舍去
当枚举的最小值的二分后,mid所代表的cnt<m了,这里代表因为枚举出来的要求的最小值偏大了,所以实际的段数更少
如:一共五个数:4 2 2 5 1,要求分成三段
枚举的8作为最小值偏大了,所以用两段就足够了,但实际上,把枚举的最大值缩小,前两段中也有数字能放进第三段
所以check检查的逻辑是:段数cnt<=m
因为比要求的段数m更少的段数cnt也可以,只是没有达到二分上mid最好的值
浮点数二分
up说不大可能会考,所以没看
高精度加法
栈

指针一开始指向栈的第一格的下面

题目
模拟栈

#include <bits/stdc++.h>
using namespace std;const int NN = 1e5 + 10;
int stk[NN];
int top = -1;void push(int x) {stk[++top]=x;
}void pop() {top--;
}bool empty() {return top==-1;
}int query() {return stk[top];
}void solve() {int m;cin >> m;while (m--) {string op;cin>>op;if (op=="push") {int x;cin>>x;push(x);} else if (op=="empty") {if(empty())cout<<"YES\n";else cout<<"NO\n";} else if (op == "pop") {if (!empty()) pop();} else{if (empty()) cout<<"empty\n";else cout<<query()<<"\n";}}
}int main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int t = 1;while (t--) solve();return 0;
}递归
对于递归,只需模拟最后两层,剩下所有的递归和最后两层是一样的
回溯
dfs一种是正常的回溯法,一种是在图上进行的dfs操作
子集枚举(递归实现指数型枚举,O(n)=2^n)
对于每个东西,是选和不选,删和不删,留和不留
一旦涉及到两个状态,就是子集枚举

对角线(额外)
主对角线(正对角线):n - j + i(主对角线是从方阵的左上角延伸到右下角的一条线,该线上每个元素的行索引和列索引相等,即i=j)
方向:从 左上到右下(↘️)数学性质:同一主对角线上的所有点满足 行号 - 列号 = 常数(即 i - j = C)
例如:点 (3,1) 和 (4,2) 在同一条主对角线上,因为 3-1 = 4-2 = 2
索引处理:
原始公式 i - j 可能为负数(如 i=1, j=2 → 1-2=-1)
通过变形 n - j + i 确保索引为正数
辅对角线(反对角线):i + j(在二维数组中,对于一个n*n的方阵,若以 0 开始计数,辅对角线元素的行索引 i 和列索引 j 满足i + j = n - 1)
方向:从 右上到左下(↙️)
数学性质:同一副对角线上的所有点满足 行号 + 列号 = 常数(即 i + j = C)
例如:棋盘上的点 (2,3) 和 (1,4) 在同一条副对角线上,因为 2+3 = 1+4 = 5
对角线的数量是2*N-1(对角线是所有斜着的线,不光是中间的那根)
题目
递归实现排列型枚举

#include <iostream>
using namespace std;const int NN=10;
int path[NN];
bool vis[NN];
int n;void dfs(int u){//出递归if(u>n){for(int i=1;i<=n;i++){cout<<path[i]<<" ";}cout<<"\n";return;}//for(int i=1;i<=n;i++){if(!vis[i]){vis[i]=1;//path用来记录已经确定的排列顺序path[u]=i;//下一层dfs(u+1);//回溯vis[i]=0;}}}int main()
{cin>>n;dfs(1);return 0;
}N皇后
N*N的方格放置N个皇后
即要求每一行都放置一个皇后

#include <bits/stdc++.h>
using namespace std;const int NN=20;
//fan反对角线,zhu主对角线
bool col[NN],zhu[NN],fu[NN];
int N;
int cnt=0;//i表示当前正在处理的行号,看每一行是否有位置
void dfs(int i) {//可以填棋子,如果能填完最后一行,就是一个可行解//代表当前行号的u大于要求的行数n,因为i==n时,最后一行还没有开始填if(i>N) {cnt++;return;}for(int j=1; j<=N; j++) {if(!col[j]&&!zhu[N-j+i]&&!fu[i+j]) {//dfs()中的数是按行枚举,如果这个位置有了,它所在的列、主对角线、反对角线不能有棋子//在这个位置有棋子时,可以标记所在的列、主对角线、反对角线为访问过,下次不能访问col[j]=1;zhu[N-j+i]=1;fu[i+j]=1;//访问下一个dfs(i+1);//回溯col[j]=0;zhu[N-j+i]=0;fu[i+j]=0;}}
}void solve() {cin>>N;dfs(1);cout<<cnt;
}int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;while(t--)solve();return 0;
}递归实现指数型枚举(n<=25都可以用)
题目解析
x代表不选,数字代表选了,?代表正在选

代码
#include<bits/stdc++.h>
using namespace std;const int N = 16;
int n;
//status,表示选或不选的状态
bool st[N];//u是当前正在处理的数字
void dfs(int u) {//当u>n时,所有数字遍历完,遍历st数组,打印所有st[i]=1的数字if(u>n) {for(int i=1;i<=n;i++) {if(st[i]) cout<<i<<" ";}cout<<endl;return;}//选和不选在这里就是一种回溯,改变顺序会有影响,这里是先不选后选的情况//不选ust[u]=0;//处理下一个数字dfs(u+1);//选ust[u]=1;//处理下一个数字dfs(u+1);
}
int main() {cin >> n;dfs(1);return 0;
}二进制枚举(O(n)=n*2^n)

基本位运算:
左移<<:二进制位中,在右边补0
这里1<<3,在二进制中补三个0,就是1000,就是8
对于一个十进制数:
<<1,就是*2
>>1,就是/2
&1,就是保留二进制位最后一位的值
#include <bits/stdc++.h>
using namespace std;
int main() {int n;cin >> n; // 输入集合的大小 n// 遍历所有可能的子集(2^n 种)for (int i = 0; i < (1 << n); i++) {// 检查每个元素是否被选中for (int j = 0; j < n; j++) {if ((i >> j & 1) == 1) { // 如果 i 的第 j 位为 1// 这里可以处理选中的元素// 例如:输出选中的元素cout << j << " ";}}cout << "\n"; // 换行,表示一个子集结束}return 0;
}行==0或列==0或对角线==0,五子棋也没有获胜(额外)
当 row 或者 col 的值等于 0 时,这表明当前行或者当前列上没有放置任何一方的棋子,或者全部放置的是另一方的棋子
在代码逻辑里,同样把这种情况视为一方获胜(因为另一方没有在这一行或列落子),所以也判定当前棋盘状态不是平局对于主对角线和辅对角线也同理
题目
五子棋对弈

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
int a[30];//用一维数组从棋子落子情况,存放棋子是1还是0
int b[10][10];//用二维数组存棋盘
int ans=0;bool check(){int pos=0;for(int i=0;i<5;i++){for(int j=0;j<5;j++){//把棋子落子情况从一维转成二维b[i][j]=a[pos++];}}//行和列棋子的情况for(int i=0;i<5;i++){int row=0,col=0;for(int j=0;j<5;j++){row+=b[i][j];//从左向右加,就是行col+=b[j][i];//从上向下加,就是列}//行或列连成5颗棋子,不是平局if(row==0||row==5||col==0||col==5)return false;}//对角线棋子的情况int zhu=0,fu=0;for(int i=0;i<5;i++){//主对角线i=jzhu+=b[i][i];//辅对角线i+j=n-1fu+=b[i][4-i];}//对角线连成5颗棋子,不是平局if(zhu==0||zhu==5||fu==0||fu==5)return false;return true;
}int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n=25;//遍历所有子集for(int i=0;i<(1<<n);i++){int cnt=0;//检查每个元素for(int j=n-1;j>=0;j--){if((i>>j&1)==1)cnt++;//用数组存棋盘中落子情况,表示棋盘第j位的棋子是1还是0a[j]=(i>>j&1);}//一个25格,下满棋盘,所以白子13个,黑子12个if(cnt!=13)continue;if(check())ans++;}cout<<ans;return 0;
}dfs和bfs题目
acwing,课程中的kuangbin
登录 - AcWing
bfs格式
bfs使用队列维护数据
在 BFS(广度优先搜索)中,使用队列(Queue)来维护待处理的节点,是因为 BFS 的核心思想是 按层级逐步扩展搜索,而队列的 先进先出(FIFO) 特性正好符合这一需求
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'//最大常量
const int NN=;
//对于图的搜索,可能需要地图
char g[NN][NN][NN];
//访问数组,如果题目状态唯一,没有重复和无意义的搜索路径,不需要访问数组
bool vis[NN][NN][NN];
//答案数组,如果题目结果唯一,不存在多个有效答案需要记录,不需要答案数组
int ans[NN][NN][NN];struct point{int x,y,z;
};
//使用队列,看情况使用结构体
queue<point> que;//对于位置方向的移动,一般使用偏移量,看情况可能是一维、二维、三维
//{}中写出偏移量
//在某些题目不写偏移量
int dx[]={};
int dy[]={};
int dz[]={}int bfs(){while(!que.empty()){//得到队列首元素auto p=que.front();//队头扩展搜索完毕后出队,避免重复搜索que.pop();//一维位置移动问题//当当前位置x等于目标位置k时,就找到了最短路径,直接返回//if(p==k)return ans[p];//循环,进行遍历for(){//这个点的位置再加上偏移量就是下个点的位置//nx的n表示nextint nx=p.x+dx[i], ny=p.y+dy[i], nz=p.z+dz[i];//对边界的判断if(){//状态更新vis[nx][ny][nz]=1;//答案更新,下一个的位置就是上一个+1ans[nx][ny][nz]=ans[p.x][p.y][p.z]+1;//三维迷宫问题//return语句处于if判断之中。因为一旦找到了目标位置,就意味着找到了最短路径,直接返回if() return ans[nx][ny][nz];//没有得到答案就入队que.push({nx,ny,nz});}}}//如果0也是可能的答案,就return -1;return 0;
}int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);while(){// 初始化(多个样例)memset(vis,0,sizeof(vis));memset(ans,0,sizeof(ans));queue<point> empty; swap(que, empty);// 读入for(int i=1;i<=L;i++){for(int j=1;j<=R;j++){for(int k=1;k<=C;k++){//读入地图cin>>g[i][j][k];if(g[i][j][k]=='S'){//放入起点que.push({i,j,k});vis[i][j][k]=1;}}}}//答案cout<<bfs();}return 0;
}坐标系
二维网格坐标系
和数学的笛卡尔坐标系不同,X向下,Y向右
在三维坐标系中,通常采用 右手坐标系(X向右,Y向前,Z向上)
// 右、左、前、后、上、下 int dx[] = {1, -1, 0, 0, 0, 0}; int dy[] = {0, 0, 1, -1, 0, 0}; int dz[] = {0, 0, 0, 0, 1, -1};
棋盘问题(dfs)

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'const int NN=20;
int n,k,ans=0;
char g[NN][NN];//表示棋盘
bool col[NN];//代表每一行的每一列是否有棋子//u:行,sum:总棋子数
void dfs(int u,int sum){//符合条件得到答案,退出if(sum==k){ans++;return;}//超出边界,退出//先得到答案,再退出,如果先判断超出边界,无论sum 是否等于 k,都会直接返回if(u>n)return;//遍历每一列for(int i=1;i<=n;i++){if(!col[i]&&g[u][i]=='#'){col[i]=1;dfs(u+1,sum+1);col[i]=0;}}//这一行不能放棋子(没有#的情况),直接去下一行dfs(u+1,sum);
}int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);while(cin>>n>>k,n!=-1&&k!=-1){//每一次输入都要初始化访问数组和答案memset(col,0,sizeof(col));ans=0;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>g[i][j];}}dfs(1,0);//枚举每一行cout<<ans<<endl;}return 0;
}地牢大师(三维迷宫bfs)


#include <bits/stdc++.h>
using namespace std;
#define endl '\n'const int NN=110;
char g[NN][NN][NN];
int ans[NN][NN][NN];
bool vis[NN][NN][NN];
int L,R,C;
struct point{int x,y,z;
};
queue<point>que;int dx[]={1,-1,0,0,0,0};
int dy[]={0,0,1,-1,0,0};
int dz[]={0,0,0,0,1,-1};//看情况bfs类型是int还是void
int bfs(){while(!que.empty()){auto p=que.front();que.pop();for(int i=0;i<6;i++){int nx=p.x+dx[i],ny=p.y+dy[i],nz=p.z+dz[i];if(nx>=1&&nx<=L&&ny>=1&&ny<=R&&nz>=1&&nz<=C&&!vis[nx][ny][nz]&&g[nx][ny][nz]!='#'){vis[nx][ny][nz]=1;ans[nx][ny][nz]=ans[p.x][p.y][p.z]+1;if(g[nx][ny][nz]=='E')return ans[nx][ny][nz];que.push({nx,ny,nz});}}}return 0;
}int main(){while(cin>>L>>R>>C,L!=0&&R!=0&&C!=0){//初始化memset(vis,0,sizeof(vis));memset(ans,0,sizeof(ans));queue<point>empty;swap(que,empty);//读入for(int i=1;i<=L;i++){for(int j=1;j<=R;j++){for(int k=1;k<=C;k++){cin>>g[i][j][k];if(g[i][j][k]=='S'){vis[i][j][k]=1;que.push({i,j,k});}}}}int res=bfs();if(res)printf("Escaped in %d minute(s).\n",res);else cout<<"Trapped!"<<endl;}return 0;
}抓住那头牛(一维位置移动bfs)

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'//N,K上限是1e5,但是X有2*X的情况,所以X上限是2*1e5
const int NN=2e5+10;
int ans[NN];
bool vis[NN];
int N,K;
queue<int>que;int dx[]={-1,1,2};int bfs(){while(!que.empty()){auto x=que.front();que.pop();//当前位置 x 等于目标位置 K 时,就找到了最短路径,直接返回对应的步数 ans[x]if(x==K)return ans[x];for(int i=0;i<3;i++){int nx;if(dx[i]==2)nx=x*dx[i];else nx=x+dx[i];//边界判断if(nx>=0&&nx<NN&&!vis[nx]){vis[nx]=1;ans[nx]=ans[x]+1;que.push(nx);}}}return -1;
}int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>N>>K;vis[N]=1;que.push(N);cout<<bfs();return 0;
}找倍数(状态唯一,没有访问数组,结果唯一,没有答案数组bfs)

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define int long longint n;
queue<int>que;int bfs(){while(!que.empty()){auto p=que.front();que.pop();if(p%n==0)return p;//*10,相当于在末尾补0que.push(p*10);//*10+1,相当于在末尾补1que.push(p*10+1);}return -1;
}signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);while(cin>>n,n!=0){queue<int>empty;swap(que,empty);//不考虑前导0,直接将1放入队列que.push(1);cout<<bfs()<<endl;}return 0;
}质数路径(位权)

#include <bits/stdc++.h>
using namespace std;const int N = 10010; // 四位数的最大范围是9999,多一点,避免数组越界
int ans[N]; // 记录操作数
bool vis[N]; // 访问标记
int a[4]; // 存放数字的各位
int d[4] = {1000, 100, 10, 1}; // 位权偏移量
queue<int> que;
int A, B;// 判断一个数是否为素数
bool isPrime(int num) {if (num < 2) return false;for (int i = 2; i * i <= num; i++) {if (num % i == 0) return false;}return true;
}int bfs() {while (!que.empty()) {int p = que.front();que.pop();if (p == B) return ans[p];// 分解数字各位//每次迭代结束时,先执行 i/=10,再执行 j--(如果颠倒不行)//当 i 变为 0 时,循环立即终止,不会执行多余的 j--//防止j变成负数,数据越界for (int i = p, j = 3; i > 0; i /= 10,j--) {a[j] = i % 10;}// 尝试修改每一位for (int j = 0; j < 4; j++) {//遍历给出数字的每一位for (int i = 0; i < 10; i++) {//对于每一位 j,这尝试将该位数字修改为 0 ~9 中的任意一个值//优化if (j == 0 && i == 0) continue; // 千位不能为0//计算将数字 p 的第 j 位修改为 i 后得到的新数字 nx。//其中 d[j] 是位权偏移量数组 d 中对应第 j 位的位权(如千位是 1000,百位是 100 等)//a[j] 是数字 p 当前第 j 位的原始数字。int nx = p + d[j] * (i - a[j]);if (nx >= 1000 && nx < N && isPrime(nx) && !vis[nx]) {vis[nx] = 1;ans[nx] = ans[p] + 1;que.push(nx);}}}}return -1; // 如果无法到达
}int main() {int T;cin >> T;while (T--) {cin >> A >> B;//初始化memset(ans, 0, sizeof(ans));memset(vis, 0, sizeof(vis));queue<int>empty;swap(que,empty);//放入起点que.push(A);vis[A] = 1;int res = bfs();if (res != -1) {cout << res << endl;} else {cout << "Impossible" << endl;}}return 0;
}代码解析(新整数=原整数+对应位权*对应数位变化量)
(i - a[j]) 计算的是将整数 p 的第 j 位从 a[j] 修改为 i 时,该位数字的变化量
例如,如果 a[j] = 3,i = 5,那么 (i - a[j]) = 5 - 3 = 2,表示该位数字需要增加 2
d[j] * (i - a[j]) 则是将该位数字的变化量乘以对应的位权,得到由于这一位数字变化对整个整数的影响值。例如,对于百位(d[1] = 100),如果数字变化量是 2,那么 d[1] * (i - a[1]) = 100 * 2 = 200,表示百位数字变化 2 会使整个整数变化 200
p + d[j] * (i - a[j]) 就是在原整数 p 的基础上,加上由于第 j 位数字变化对整个整数的影响值,从而得到修改后的新整数 nx
罐子(把操作看成二维坐标)
把两个罐子倒水的操作看成二维坐标

题目

#include <bits/stdc++.h>
using namespace std;struct Point {// 当前两个容器的水量int x, y;// 操作步骤记录//定义成string类型,将多个操作编号按顺序拼接起来string steps;
};const int NN = 110;
string op[6] = {"FILL(1)", "FILL(2)", "DROP(1)", "DROP(2)", "POUR(1,2)", "POUR(2,1)"
};int ans[NN][NN]; // 记录到达每个状态的最少步数
bool vis[NN][NN]; // 标记状态是否被访问过
queue<Point> que;
int a, b, c; // 容器容量和目标水量int bfs() {while (!que.empty()) {auto p = que.front();que.pop();// 检查是否达到目标if (p.x == c || p.y == c) {cout << ans[p.x][p.y] << endl;//在结构体中,每一个操作都拼接成了一个字符串,用增强for获得每一个操作,变成数字for (char i : p.steps) {cout << op[i - '0'] << endl;}return 0;}// 计算6种操作的水量变化//pour1 表示从罐子 x(容量为 a)向罐子 y(容量为 b)倒水时,能够倒过去的水量//取 p.x(罐子 x 当前的水量)和 b - p.y(罐子 y 还能容纳的水量)中的较小值int pour1 = min(p.x, b - p.y); // POUR(1,2)int pour2 = min(a - p.x, p.y); // POUR(2,1)//两个罐子的变化量,六个操作对应六个值int dx[] = {a - p.x, 0, -p.x, 0, -pour1, pour2};int dy[] = {0, b - p.y, 0, -p.y, pour1, -pour2};for (int i = 0; i < 6; i++) {int nx = p.x + dx[i];int ny = p.y + dy[i];// 检查新状态是否合法且未访问if (nx >= 0 && nx <= a && ny >= 0 && ny <= b &&!vis[nx][ny]) {vis[nx][ny] = 1;ans[nx][ny] = ans[p.x][p.y] + 1;//结构体中定义了操作步骤是string,用+可以拼接que.push({nx, ny, p.steps + to_string(i)});}}}return -1;
}int main() {cin >> a >> b >> c;memset(ans, 0, sizeof ans);memset(vis, 0, sizeof vis); //放入起点,一开始两个罐子都是空的,且没有操作que.push({0, 0, ""});vis[0][0] = 1;int res=bfs();if(res==-1)cout<<"impossible"<<endl;return 0;
}全球变暖(两个bfs)

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'const int NN = 1010;
char g[NN][NN];
bool vis[NN][NN];
struct Point {int x, y;
};
queue<Point> que; // 全局队列
int dx[] = {-1, 0, 1, 0};
int dy[] = {0, 1, 0, -1};
int N, sum=0, notYanMo=0;// 判断岛屿是否会被完全淹没
bool willBeFlooded(int x, int y) {queue<Point> empty;swap(que, empty);// 清空队列que.push({x, y});vis[x][y] = 1;bool isFlooded = true; // 初始假设会被淹没while (!que.empty()) {auto p = que.front();que.pop();//必须在 while 循环内部,确保每次处理新的陆地节点时,都能正确判断其是否有邻接海洋bool hasAdjacentSea = false; // 当前陆地是否有邻接海洋for (int i = 0; i < 4; i++) {int nx = p.x + dx[i];int ny = p.y + dy[i];if (nx >= 1 && nx <= N && ny >= 1 && ny <= N) {if (g[nx][ny] == '.') {hasAdjacentSea = true; // 当前陆地有邻接海洋} else if (g[nx][ny] == '#' &&!vis[nx][ny]) {que.push({nx, ny});vis[nx][ny] = 1;}}}// 如果当前陆地没有邻接海洋,整个岛屿不会被完全淹没if (!hasAdjacentSea) {isFlooded = false;}}return isFlooded;
}void bfs() {memset(vis, 0, sizeof(vis));for (int i = 1; i <= N; i++) {for (int j = 1; j <= N; j++) {if (g[i][j] == '#' &&!vis[i][j]) {//因为willBeFlooded函数对每个陆地都bfs了//所以bfs函数中的!vis[i][j] 保证了这个位置没有被其他 BFS 过程访问过//所以当进入这个分支时,意味着发现了一个新的、独立的岛屿sum++;//连通岛总数if (!willBeFlooded(i, j)) {notYanMo++;}}}}
}int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> N;for (int i = 1; i <= N; i++) {for (int j = 1; j <= N; j++) {cin >> g[i][j];}}bfs();cout << sum - notYanMo << endl;return 0;
}代码解析(isFlooded和hasAdjacentSea的bool值)

组合数

不选第n个数,在n-1个数中选m个数,就是n个数中选m个数的部分方案数
选第n个数,在n-1个数中,选择m-1个数,把这第n个数一加,就是n个数中选m个数的部分方案数
题目
递归求组合数

#include <iostream>
using namespace std;int n,m,t;int f(int m,int n){if(n==m||m==0)return 1;return f(m-1,n-1)+f(m,n-1);
}void solve(){cin>>n>>m;int ans=0;ans=f(m,n);cout<<ans<<"\n";
}int main()
{cin>>t;while(t--)solve();return 0;
}记忆化搜索
数组的维度通常与问题的状态空间一致:
与dfs函数的参数一致
实现搜索函数:
检查当前状态是否已经被计算过
这一步要在递归边界下面写
一般写dfs函数,返回值是void,使用记忆化搜索,dfs的返回值写成int

#include <bits/stdc++.h>
using namespace std;//1.定义记忆化数组
//记忆化数组的维度和问题的状态空间一致
//因为问题是求斐波那契数列,只有一个参数,所以一维
int dp[50];int f(int n){//递归边界if(n==1||n==2)return 1;//3.实现搜索函数,检查当前状状态是否被计算过//这一步放在递归边界下if(dp[n]!=-1)return dp[n];//3.实现搜索函数,保存记忆化数组//本来return f(n-1)+f(n-2);//增加一个dp[n]=return dp[n]=f(n-1)+f(n-2);
}int main(){//2.初始化记忆化数组memset(dp,-1,sizeof(dp));cout<<f(19);return 0;
}题目
01背包
01 背包,即一种 DP 问题,以放置物品为模型,每个物品只能放一次

题目解题
递归分治
分而治之:将问题分解为若干子问题,递归解决子问题,最后合并结果无记忆化:子问题可能被重复计算,导致效率低下
特点
自顶向下:从原问题出发,逐步分解为子问题可能重复计算:同一子问题会被多次求解(这个背包问题)
代码直观:直接反映问题逻辑,但时间复杂度高
dfs(1,0)往右,表示对第一个物品选,到dfs(2,1)表示第一个物品选了,虽然参数是2,但第二个物品还没有选
这个dfs不是当前的状态,而是当前选完之后会进入到的状态
(代码中,我的变成习惯是从1开始到i<=N,所以第一个物品在索引为1的位置,别的代码可能在索引为0的位置)
代表选的ans2的ans2=dfs(u+1,sum+v[u])+w[u]是递归(题中是价值)返回值的累加
如:dfs(4,5),因为选了第三个物品,第三个物品的价值是四,把4带回去
代码
不用记忆化搜索(时间复杂度2^n,超时)
#include<bits/stdc++.h>
using namespace std;const int N=1010;
int w[N],v[N];
int n,m;int dfs(int u,int sum) {//u代表当前选择的是第几个物品//sum表示当前的总体积,用当前体积隔离不同递归层的状态,没有(用数组的)显式回溯的使用//递归函数返回值代表最大价值if(u>n) {return 0;}//ans1不选,ans2选int ans1=0,ans2=0;//ans1不选,直接跳过第u个物品,ans1=dfs(u+1,sum);//ans2选第u个物品,并增加价值 w[u]//这里的ans2=dfs(u+1,sum+v[u])+w[u]是递归返回值的累加if(sum+v[u]<=m) ans2=dfs(u+1,sum+v[u])+w[u];return max(ans1,ans2);
}
int main() {cin>>n>>m;for(int i=1; i<=n; i++) cin>>v[i]>>w[i];cout<<dfs(1,0);
}使用记忆化搜索
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int w[N],v[N];
//1.定义记忆化数组,参数和递归函数参数一样
int dp[N][N];
int n,m;int dfs(int u,int sum) {
//u代表当前选择的是第几个物品
//sum表示当前的总体积
//递归函数返回值代表最大价值if(u>n) {return 0;}//3.搜索的时候记忆// - 在递归边界下判断当前状态是否访问过,访问过,直接返回if(dp[u][sum]!=-1) return dp[u][sum];//ans1是不选,ans2是选int ans1=0,ans2=dfs(u+1,sum);if(sum+v[u]<=m) ans1=dfs(u+1,sum+v[u])+w[u];// - 没访问过,正常搜索,记忆下来return dp[u][sum]=max(ans1,ans2);
}int main() {//2.初始化记忆化数组为 -1memset(dp,-1,sizeof(dp));cin>>n>>m;for(int i=1; i<=n; i++) cin>>v[i]>>w[i];cout<<dfs(1,0);
}使用动态规划
01背包问题,也是选与不选的问题,可以通过子集枚举枚举出来,但是子集枚举时间复杂度为2^n,很高

如果不选,就从上面转移过来,如果选
看选这个物品和不选这个物品那个是最优的
dp[ i ][ j ]=max(dp[ i-1 ][ j-v[ i ]]+w[ i ],dp[ i-1 ][ j ]);
如图:对于dp[ 2 ][ 2 ],选是从dp[ 1 ][ 0 ]过来,不选是从dp[ 1 ][ 2 ]过来
所以代码中选要 j-v[ i ]
#include <bits/stdc++.h>
using namespace std;const int N=1010;
int dp[N][N];
int n,m;int main() {cin>>n>>m;for(int i=1;i<=n;i++)cin>>v[i]>>w[i];//第一维枚举每件物品for(int i=1;i<=n;i++){//第二维枚举体积for(int j=0;j<=m;j++){if(j<v[i]){//如果容积不够,不能选dp[i][j]=dp[i-1][j];}else{//容积够,能选这个物品//看选这个物品和不选这个物品那个是最优的dp[i][j]=max(dp[i-1][j-v[i]]+w[i],dp[i-1][j]);}/*优化//默认不选dp[i][j]dp[i-1][j];if(j>=v[i]){//当容积允许选第i件物品时,才选dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);}*/}}cout<<dp[n][m];return 0;
}数组分割(没看)

#include <bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int a[N];
int dp[N][2];//统计奇偶性
int n;
const int mod=1000000007;
int dfs(int u,int sum) { //前u个数中选出奇偶性为1/0if(u>n) {//如果奇偶性总和sum是0,是偶数,return 1;是奇数,return 0return sum==0;}if(dp[u][sum]!=-1) return dp[u][sum];//对数字有选和不选,进行判断int ans=0;if(a[u]%2==1) {//当前这个数是奇数//dfs(u+1,sum^1),选这个数//如果当前的数是奇数,奇数+奇数就是偶数,奇偶性sum变成0//dfs(u+1,sum),不选这个数ans=ans+dfs(u+1,sum^1)+dfs(u+1,sum);} else {//当前这个数是偶数//dfs(u+1,sum),奇数选偶数奇偶性不变//dfs(u+1,sum),不选这个数,奇偶性也不便ans=ans+dfs(u+1,sum)+dfs(u+1,sum);}//可以合二为一,直接写成dfs(u+1,sum^(a[u]%2))+dfs(u+1,sum);return dp[u][sum]=ans%mod;
}
void solve() {int sum=0;cin>>n;for(int i=1; i<=n; i++) //只关注奇偶性,范围缩小for(int i=1; i<=n; i++) {//多组测试数据,手动初始化dpdp[i][0]=dp[i][1]=-1;int x;cin>>x;x%=2;a[i]=x;sum+=a[i];}//总和为奇数,只能拆成一组偶数,用一组奇数,不能拆成两组都为偶数if(sum%2==1) {cout<<"0\n";return;}cout<<dfs(1,0);
}
int main() {int t;cin>>t;while(t--) solve();return 0;
}动态规划
动态规划,O(n)=n^3,对于n<=100的情况下使用的算法
动态规划的特点:
有后效性,当前的决策会影响到后面的决策。具有最优子结构的特征
解这类题的步骤:
1.定义数组(数学归纳法中的定义函数):如dp[i](dp代表方案)表示的是什么,时刻记住定义的数组的含义2.初始化dp:初始化dp,初始化的方法有两种:根据数组定义来写或根据实际意思。
3.遍历所有的情况:用子结构递推到最终的结果
4.写状态转移方程:dp[i]由前一个怎样转移过来的
题目
李白打酒加强版(三维dp)


#include<bits/stdc++.h>
using namespace std;const int mod=1e9+7;
const int NN=110;//1.定义数组
//含义:dp是前i个店遇到j朵花,剩k斗酒的方案
int dp[NN][NN][NN];//三维dp数组
int n,m;int main()
{cin>>n>>m;//2.初始化//这里根据数组定义写//题目:一天,他提着酒壶,从家里出来,酒壶中有酒 2 斗,所以遇0店0花有2酒方案数是1dp[0][0][2]=1;//3.遍历所有的情况for(int i=0;i<=n;i++){for(int j=0;j<=m-1;j++){if(i==0&&j==0) continue; for(int k=0;k<=100;k++)//因为最多出现100次操作2,故va最大为100{//4.写状态转移方程:dp[i]由什么转移过来//i代表店,逢店加一倍。所以对于i-1时,是从k/2的状态转移到k的//因为i-1,所以i>=1。因为k/2,所以k要是偶数if(k%2==0&&i>=1) dp[i][j][k]=(dp[i][j][k]%mod+dp[i-1][j][k/2]%mod)%mod;//j代表花,遇花喝一斗。所以对于j-1,是从k+1的状态转移到k的if(j>=1) dp[i][j][k]=(dp[i][j][k]%mod+dp[i][j-1][k+1]%mod)%mod;}}}//最后的结果,题目:最后一次遇到的是花,他正好把酒喝光了//即对于花m-1的情况,还有1酒cout<<dp[n][m-1][1]%mod;
}跳石头(使用bitset的dp)

#include <bits/stdc++.h>
using namespace std;const int NN=4e4+10;/*
这个数组的大小是 MAXN,即数组有 MAXN 个元素
而数组中的每个元素的类型是 bitset<MAXN> 。即,数组的每个元素本身都是一个 bitset 对象
每个这样的 bitset 对象可以存储 MAXN 个二进制位
*/
bitset<NN> dp[NN];
int c[NN];int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n;cin>>n;for(int i=1;i<=n;i++)cin>>c[i];int ans=0;//动态规划的依赖关系:dp [j] 依赖于 dp [j + c [j]] 和 dp [2*j],即 后面的状态会影响前面的状态//如果从 j = 1 开始,dp[j + c[j]] 和 dp[j * 2] 可能还未计算,导致错误for(int j=n;j>=1;j--){/*bitset 的本质是 二进制位数组,每一位只能是 0 或 1f因此,dp[j][c[j]] = 1 就是在 dp[j] 的二进制位中,把第c[j]位设为1,表示这个数字可以被访问*/dp[j][c[j]]=1;/*dp[j + c[j]] 存储了从位置 j + c[j] 出发能到达的状态集合,dp[2*j] 存储了从位置 2*j 出发能到达的状态集合通过按位或操作,将这些状态集合合并到 dp[j] 中即从位置 j 出发不仅能到达自身直接能到达的状态,还能到达通过 j + c[j] 或 2*j 这些位置能到达的状态*/if(j+c[j]<=n)dp[j]|=dp[j+c[j]];if(2*j<=n)dp[j]|=dp[2*j];/*利用 bitset 的 count() 函数统计 dp[j] 中值为 1 的位的数量即从位置 i 出发能到达的不同状态的数量通过不断更新 ans 取最大值,最终得到小明最多能获得的分数*/ans=max(ans,(int)dp[j].count());}cout<<ans;return 0;
}dijkstra(最短路)
图-最短路径-Dijkstra(迪杰斯特拉)算法_哔哩哔哩_bilibili
dijkstra算法求单元最短路问题,即图中某一确定的点到另一点的最短路
使用堆(优先队列)时,堆能够自动依据距离对所有点进行排序。在每一轮迭代时,直接从堆顶取出当前距离源点最近的点

邻接表存储图(额外)
//用邻接表存图
int h[NN],e[NN],ne[NN],w[NN],idx;
void add(int a,int b,int c){w[idx]=c;e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}dijkstra模板
#include <bits/stdc++.h>
using namespace std;//注意:对于无向图,边的存储量是实际的2倍,看情况提高最大值
const int NN= ;
int n,m;typedef pair<int,int> PII; //first存距离,second存结点编号//dist储从起点(源点)到各个结点的当前最短距离
//st标记某个结点的最短距离是否已经确定
int dist[NN],st[NN];//用邻接表存图
int h[NN],e[NN],ne[NN],w[NN],idx;
void add(int a,int b,int c) {w[idx]=c;e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}int dijkstra() {memset(dist,0x3f,sizeof(dist)); // 将所有距离初始化正无穷priority_queue<PII, vector<PII>, greater<PII>> heap; // 小根堆dist[1] = 0; // 第一个点到起点的距离为 0//把 1 号点放入堆中,0代表到1号点的最短路径,1是坐标heap.push({0,1});while(!heap.empty()) { // 堆不空//找到当前距离最小的点auto p = heap.top();heap.pop();//second就是点的编号,如果这个点的最短路确定了,就不用更新其他点了if(st[p.second]) continue;st[p.first] = true;//标记p已经确定最短路// 遍历节点 p.second 的所有邻边(p.second 是当前距离起点最近的节点)for(int i = h[p.second]; i != -1; i = ne[i]) {// e[i] 是当前边的终点(即 p.second 的邻居节点)int j = e[i];// 如果从起点到 j 的当前最短距离 > 从起点到 p.second 的最短距离 + 当前边的权重if(dist[j] > dist[p.second] + w[i]) {// 更新到 j 的最短距离dist[j] = dist[p.second] + w[i];// 将 {新距离, 节点j} 加入堆heap.push({dist[j], j});}}}// 说明 1 和 n 是不连通的,不存在最短路if(dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}int main() {//h 数组存储的是每个顶点的第一条边在 e 数组中的索引//若 h[i] 为 -1,则表示顶点 i 没有出边memset(h,-1,sizeof(h));cin >> n >> m;while(m--) {int a,b,c;cin>>a>>b>>c;add(a,b,c);//add(b,a,c); //如果题目要求双向,再来add}cout << dijkstra();return 0;
}题目

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'//注意:对于无向图,边的存储量是实际的2倍
const int NN=2e5+10;
int n,m;
int a[NN];typedef pair<int,int> PII; //first存距离,second存结点编号
int dist[NN],st[NN];//用邻接表存图
int h[NN],e[NN],ne[NN],w[NN],idx;
void add(int a,int b,int c){w[idx]=c;e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}int dijkstra(){memset(dist,0x3f,sizeof(dist)); // 将所有距离初始化正无穷priority_queue<PII, vector<PII>, greater<PII>> heap; // 小根堆//把 1 号点放入堆中,0代表到1号点的最短路径,1是坐标heap.push({0,1}); dist[1] = 0; // 第一个点到起点的距离为 0while(!heap.empty()) // 堆不空{//找到当前距离最小的点auto p = heap.top();heap.pop();//second就是点的编号,如果这个点的最短路确定了,就不用更新其他点了if(st[p.second]) continue;st[p.second] = true;//标记p已经确定最短路//i赋值成头节点,一直遍历到下一条边for(int i = h[p.second]; i!=-1; i=ne[i]){//取出这个节点孩子的编号int j = e[i];//题目中:dist[j]是未确定的最短路的点,w[i]是路程的时间,a[j]是隔离的时间if(dist[j] > dist[p.second] + w[i]+a[j]){dist[j] = dist[p.second] + w[i]+a[j];heap.push({dist[j],j}); //入堆}}}// 说明 1 和 n 是不连通的,不存在最短路if(dist[n] == 0x3f3f3f3f) return -1; return dist[n];
}int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);//h 数组存储的是每个顶点的第一条边在 e 数组中的索引//若 h[i] 为 -1,则表示顶点 i 没有出边memset(h,-1,sizeof(h));cin>>n>>m;for(int i=1;i<=n;i++)cin>>a[i];while(m--){int x,y,z;cin>>x>>y>>z;//x,y是两个顶点,z是权重,题目要求路线双向,所以两个add构建无向图add(x,y,z);add(y,x,z);}//到第n个城市不需要隔离,要把n减掉int res=dijkstra();if(res!=-1)cout<<res-a[n];return 0;
}数学
求最大公因数(最大公约数)
欧基里得算法(辗转相除法)
BV19r4y127fu
公约数(公因数):一个能被若干个整数同时均整除的整数
- 求 A 和 B 的最大公因数,除法关系
- (A,B)=(B,R)
- 求到最后,R=0,B 就是最大公因数

//求最大公因数
int GCD(int a,int b){if (a%b==0)return b;else return GCD(b,a%b);
}求最小公倍数
- 两个数相乘,然后除以它们的最大公因数
//求最小公倍数
int LCM(int a,int b){return ((a*b)/GCD(a,b));
}C++17自带lcm函数
分解质因数
给定正整数,打印出所有的因数都是质数
对正整数n进行分解质因数,先找到一个最小的质数
1.该正整数n为质数,则说明不需要分解
2.如果该正整数n不是质数,但是能被最小的质数整除,就打印最小的质数,然后从正整数n除以最小质数,作为新的正整数重复执行1和2
从小到大遍历 i
循环从 i=2 开始,逐步增加 i
由于 i 从小到大遍历,第一个满足 x % i == 0 的 i 一定是 x 的最小质因数:
如果 i 是合数,它一定已经被更小的质因数分解过:
例如 i=4:
如果 x % 4 == 0,说明 x 是 4 的倍数。
但 4 本身可以分解为 2*2,所以 x 一定已经被 i=2 分解过。
因此,x 不可能再被 4 整除(因为 2 已经分解完了)
结论:i 只会是质数,因为合数因数已经被更小的质因数分解
if(n>1):
处理可能剩余的大于sqrt(n)的质因数
假设输入 n = 15
首先,i = 2,15 % 2 != 0,不执行内层循环。
接着,i = 3,15 % 3 == 0,进入内层循环,n 变为 5
此时,i = 4,4 * 4 > 5,外层循环结束
此时 n = 5 > 1,需要处理
//分解质因数核心步骤//用 i*i <= n 动态判断,整数运算更快,用i<=sqrt(n)慢for(int i=2;i*i<=n;i++){//确认当前的 i 是否为 n 的因数。只有当 n 能被 i 整除时,i 才有可能是 n 的质因数if(n%i==0){//内层的 while 循环来进一步分解 n 中包含的所有 i 因子while(n%i==0){n/=i;}}}// 处理可能剩余的大于 sqrt(n) 的质因数if(n>1){//...}唯一分解定理(额外)
完全平方数

题目解析
由唯一分解定理:任何一个数,都可以分解成若干个质数的乘积
如果这个数是完全平方数,那么这若干个质数的指数一定是偶数
对于本题,需要记录指数不是偶数的数字
代码
#include <bits/stdc++.h>
using namespace std;
#define int long longsigned main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n;cin>>n;map<int,int>mp;//分解质因数for(int i=2;i*i<=n;i++){while(n%i==0){n/=i;//这里i就是分解出来的质因子//把 n 中包含的 i 因子去除,然后将 mp[i] 的值加 1,以此记录 i 作为质因数出现的次数mp[i]++;}}if(n>1)mp[n]++;int ans=1;for(auto i:mp){//如果分解出的质因子只出现了一次if(i.second%2==1)ans*=i.first;}cout<<ans;return 0;
}判断素数(欧拉筛法)
质数,又称素数,除了1和该数自身外,无法被其他自然数整除的数
1既不是质数(素数)也不是合数
平方根法(欧拉筛法)判断素数:
对于一个数字 n,根号n*根号n=n
因数是关于根号 n 对称分布的
所以只需要遍历到根号 n,如果在根号n内没有因数,那么之后也没有了
bool isPrime(int num) {//有的题目,传入的num就直接从2开始,这个if(num<2)可以不写if (num < 2) return false;//不要写sqrt,比i*i慢for (int i = 2; i * i <= num; i++) {if (num % i == 0) return false;}return true;
}模运算性质(额外)
对于减法的取模,在成为负数时,要再加上p

快速幂
蓝桥云课-快速幂
BV1nd4y1A7vF
n&1:
判断n的二进制形式最后一位是否为1
//这个mod可以不用
ll qmi(ll a,ll n,ll mod) { //计算a^nll ans=1;//用ans返回结果while(n) { //把n看成二进制,逐个处理它的最后一位if(n&1)ans=ans*a%mod;//n的最后一位是1表示这一位要计算,需要乘a,这个mod自己定义,1000或某个数a=a*a%mod;//加倍,a^2->a^4->a^8...n>>=1;//n右移1位,把n的最后一位去掉}return ans;
}
乘法逆元
乘法逆元
BV195411w75c
视频里还讲了p不是质数的情况,用扩展欧几里得算法
但题目中一般是10^9+7

欧拉算法
题目
最大公约数

筛质数

#include <bits/stdc++.h>
using namespace std;//不要用sqrt,比用i*i慢
bool isPrime(int num) {if (num < 2) return false;for (int i = 2; i * i <= num; i++) {if (num % i == 0) return false;}return true;
}int n;
int cnt=0;int main()
{cin>>n;//1既不是质数(素数)也不是合数,遍历从2开始for(int i=2;i<=n;i++){if(isPrime(i))cnt++;}cout<<cnt;return 0;
}分解质因数
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'void divide(int n){cout<<n<<"=";for(int i=2;i*i<=n;i++){if(n%i==0){while(n%i==0){cout<<i;n/=i;//如果还有剩余,输出乘号if(n>1)cout<<"*";}}}// 处理剩余的质数if(n>1)cout<<n;cout<<endl;
}int a,b;
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>a>>b;for(int i=a;i<=b;i++)divide(i);return 0;
}快速幂
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;ll qmi(ll a,ll n,ll mod){ll ans=1;while(n){if(n&1)ans=ans*a%mod;a=a*a%mod;n>>=1;}return ans;
}ll b,p,k;int main()
{cin>>b>>p>>k;cout<<qmi(b,p,k);return 0;
}乘法逆元
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define endl '\n'll p=1e9+7;
int T;ll qmi(ll a,ll n){ll ans=1;while(n){if(n&1)ans=ans*a%p;a=a*a%p;n>>=1;}return ans;
}int main()
{cin>>T;while(T--){ll N;cin>>N;cout<<qmi(N,p-2)<<endl;}return 0;
}高斯求和
高斯求和是一种快速计算连续整数和的方法

同余定理
给定一个正整数m,如果两个整数a和b满足a-b能够被m整除,即(a-b)/m得到一个整数,那么就称整数a与b对模m同余
记作a≡b(mod m)
a 和 b 除以 m 后的余数相同,即a-b是m的倍数(m能整除a-b)
即,如果a%m==b%m,(a-b)%m==0
两个数模 m 同余,所以它们的差能被 m 整除
题目
k倍区间(前缀和,同余定理,组合数)

题目解析
k=2,对1 2 3 4 5这个序列求前缀和
然后再对k进行取余
已知同余定理:对于余数相同的两个数字,它们的差能被某个正整数k整除(a≡b(mod k))
在这里,“它们的差”就是区间和(用前缀和求差就是求区间和)
而这个区间和能被k整除,符合题目要求
所以要计算不同余数,相同的次数出现了几次
然后用组合数的基本定义(组合数的基本定义是阶乘的方式,和递推公式数学本质一样)求有几个区间
因为是在出现相同余数的前缀和中选两个,即在出现的同余次数中选两个
所以公式为n(n-1)/2
对于两个不同的模 K 为 0 的前缀和,它们之间的子数组和是 K 的倍数,这样的组合数可以用组合公式 C(n, 2) = n * (n - 1) / 2 计算(从 n 个元素中选 2 个的组合数)
但是,单个模 K 为 0 的前缀和本身也算一种满足条件的情况,所以需要额外加上这 n 种情况。而 n * (n - 1) / 2 + n = n * (n + 1) / 2
代码
AC
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;int N,K;
const int NN=1e5+10;
int a[NN];
ll prefix[NN];int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>N>>K;map<int,int>mp;for(int i=1;i<=N;i++){cin>>a[i];//对每一个前缀和取模prefix[i]=(prefix[i-1]+a[i])%K;//计算不同余数出现的次数mp[prefix[i]]++;}ll ans=0;for(auto i:mp){//组合数C(n,2)=n(n-1)/2if(i.first==0){//ans+=i.second*(i.second+1)/2;//简写ans+=(ll)i.second*(i.second-1)/2+i.second;} else ans+=(ll)i.second*(i.second-1)/2;}cout<<ans;return 0;
}暴力(只通过2个)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;int N,K;
const int NN=1e5+10;
ll a[NN],prefix[NN];
int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>N>>K;for(int i=1;i<=N;i++){cin>>a[i];prefix[i]=prefix[i-1]+a[i];}int cnt=0;//求区间,O(n^2)for(int i=1;i<=N;i++){for(int j=i;j<=N;j++){if((prefix[j]-prefix[i-1])%K==0)cnt++;}}cout<<cnt;return 0;
}等差数列

等差数列求和
题目要求中包含连续的正整数相加,这就可以联想到等差数列求和公式
判断是否是2^n
bool check(int n){//如果是2^n,一直除2,最后会等于1,所以在n=1是循环停止,循环进行条件是n!=1while(n!=1){//n为偶,除2if(n%2==0)n/=2;//n是奇数且不等于1(比如 3、5 等),返回false,因为它不可能是2的幂次方数else return false;}return true;
}题目
等差数列

题目分析
题目要求项数最少,即公差 d 最大。
而由于等差数列的任意两项之差都是公差的倍数,所以我们只需要求出给出的数两两之差的最大公因数即可
代码
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'const int NN=1e5+10;
int a[NN];
int n;
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;for(int i=1;i<=n;i++)cin>>a[i];sort(a+1,a+n+1);if (a[1] == a[n]){//公差d为0的情况//都排完序了第一个和最后一个还是相等//肯定是全部都相等,直接结束cout << n << endl;return 0;}int d = a[2] - a[1];//初值设为一个公差的若干倍for (int i = 3; i <= n; i++)d = __gcd(d, a[i] - a[i - 1]);cout << (a[n] - a[1]) / d + 1 << endl;//求项数return 0;
}数字诗意

#include <bits/stdc++.h>
using namespace std;
#define int long longbool check(int n){while(n!=1){if(n%2==0)n/=2;else return false;}return true;
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n;cin>>n;int ans=0;for(int i=1;i<=n;i++){int x;cin>>x;if(check(x))ans++;}cout<<ans;return 0;
}并查集
BV1Bh4y1k7fZ
用并查集或者bfs求连通块
并查集也可以判断两个点在不在同一个集合(就是判断两个点连不连通)
并查集优化方式有:

题目
并查集

朴素代码
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'const int NN=1e5+10;
//父节点是前一个节点
int pre[NN];//函数命名成root,因为并查集,查的是元素的根节点,而且避免和stl中的find重名
int root(int x){//朴素写法//当 pre[x]=x 时,说明x的父节点就是它自身,此时x就是所在集合的根节点,直接返回 x//x不是根节点,传入pre[x],继续查找 x 的父节点的根节点,直到找到根节点为止//return pre[x]==x?x:root(pre[x]);//路径压缩优化//找到节点x的根节点后,将节点x的父节点直接设置为根节点,实现了路径压缩return pre[x]=pre[x]==x?x:root(pre[x]);
}void merge(int x,int y){//此时,x和y代表的是两个集合的根节点x=root(x),y=root(y);//x和y的根节点相同,已经在同一个集合中,此时不需要进行合并操作,直接返回if(x==y)return;//x和y不相等,分别属于不同的集合。将x的父节点设置为y(将y的父节点设置为x没区别)pre[x]=y;
}void solve(){int n,m;cin>>n>>m;//初始化,把每个节点变成自己的父节点(自环)for(int i=1;i<=n;i++) pre[i]=i;while(m--){int op,x,y;cin>>op>>x>>y;//如果操作是1,合并if(op==1)merge(x,y);else cout<<(root(x)==root(y)?'Y':'N')<<endl;}
}int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int _=1;while(_--)solve();return 0;
}路径压缩(优化)
原本
优化
优化的代码只有一个改动,在朴素代码中注释了
合根植物(是否属于同一个集合)


#include <bits/stdc++.h>
using namespace std;const int M=1000;
const int N=1000;
//父节点
int pre[M*N];
int m,n,k;int root(int x){return pre[x]=pre[x]==x?x:root(pre[x]);
}void merge(int x,int y){x=root(x);y=root(y);if(x==y)return;pre[x]=y;
}void solve(){cin>>m>>n>>k;for(int i=1;i<=m*n;i++)pre[i]=i;while(k--){int a,b;cin>>a>>b;merge(a,b);}int cnt=0;for(int i=1;i<=n*m;i++){//如果根节点等于自身,说明没有成为别人的子节点if(root(i)==i)cnt++;}cout<<cnt;
}int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int _=1;while(_--)solve();return 0;
}修改数组(先把所有可能都设置成父节点,是否出现过,出现就修改)
题目

题目分析



代码
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'const int NN=1e5+10;
int pre[NN];
int N;int root(int x){return pre[x]=pre[x]==x?x:root(pre[x]);
}void merge(int x,int y){x=root(x);y=root(y);if(x==y)return;pre[x]=y;
}int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>N;for(int i=1;i<=1e5+5;i++){pre[i]=i;}int A;for(int i=1;i<=N;i++){cin>>A;A=root(A);//找到A的根节点cout<<A<<' ';merge(A,A+1);//将A与A+1相连}return 0;
}字符串
isdigit(c)检查是否是数字字符
和c<='9'&&c>='0'效果一样
数字字符-'0'得到原本的数字
to_string(把十进制整数和浮点变成字符串)
stoi(返回对应字符串内容的整数值)
reverse(s.begin(),s.end())反转
sort(s.begin(),s.end())按字典序排序
toupper和tolower
把字符串全部转成大写或者小写
substr截取字符串
字符串基本操作
// string str1; //生成空字符串
// string str2("123456789"); //生成"1234456789"的复制品
// string str5(5, '1'); //结果为"11111"// 尾插一个字符s1.push_back('a');
//但是对于字符串,+就是连接,可以直接s1+='a',这个push_back()没用//插入字符找迭代器
//str.insert(s.begin()+i,'a')如果前面是s.begin()+i那么只能插入字符;//插入字符串找下标
// str.insert(pos,"string"如:cs):在指定的位置pos插入字符串;//string s1 = "123456789";
// s1.erase(s1.begin()+1); // 结果:13456789
// s1.erase(1);//删除1,包括1以后的所有值;//结果:1
// s1.erase(s1.begin()+1,s1.end()-2); // 结果:189//都是闭区间
// s1.erase(2,2); 从第二个位置开始是删除2后边的2个位置 // 结果:1256789//转置字符串
// reverse(s.begin(),s.end());string str=s;//string s("dog bird chicken bird cat");//字符串查找-----找到后返回首字母在字符串中的下标// 1. 查找一个字符串// if(s.find("chicken",0)!=string::npos) //代表从0下标开始,没有找到返回string::npos(通常是 4294967295 或 18446744073709551615,取决于系统)//cout << s.find("chicken") << endl; // 结果是:9// 2. 从下标为6开始找字符'i',返回找到的第一个i的下标//cout << s.find('i',6) << endl; // 结果是:11//tring s1("0123456789");//string s2 = s1.substr(2,5); // 结果:23456-----参数5表示:截取的字符串的长度题目
记数问题(数字字符-'0',to_string)

#include <bits/stdc++.h>
using namespace std;int n,x;int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>x;int cnt=0;for(int i=1;i<=n;i++){string s=to_string(i);for(int i=0;i<s.size();i++){if(s[i]-'0'==x)cnt++;}}cout<<cnt;return 0;
}统计单词数
#include <bits/stdc++.h>
using namespace std;string s1,s2;
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);//读入两行getline(cin,s1);getline(cin,s2);//全部转成大写,方便判断for(int i=0;i<s1.size();i++) s1[i]=toupper(s1[i]);for(int i=0;i<s2.size();i++) s2[i]=toupper(s2[i]);//要找给定的单词,单词是独立的,即这个单词左右两边都有空格s1=' '+s1+' ';//把句子的开头和结尾增加空格,方便找到出现在开头或结尾的单词s2=' '+s2+' ';//没有找到返回-1if(s2.find(s1)==-1){cout<<-1;}else{int cnt=0;//这个单词第一次出现的开始位置int st=s2.find(s1);int pos=st;while(pos!=string::npos){cnt++;//要找单词有多少个,即每次找到单词的位置pos之后,再从下一个位置往后找,每次找到次数cnt++pos=s2.find(s1,pos+1);}cout<<cnt<<' '<<st;}return 0;
}结构体
题目

#include <bits/stdc++.h>
using namespace std;const int NN=1010;
int N;struct Node{string name;int chinese,math,eng;int sum;int idx;
}stu[NN];//直接用Node类型声明数组stubool cmp(Node a,Node b){if(a.sum!=b.sum) return a.sum>b.sum;else return a.idx<b.idx;
}int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>N;for(int i=1;i<=N;i++){string name;int x,y,z;cin>>name>>x>>y>>z;stu[i]={name,x,y,z,x+y+z,i};}//自定义排序sort(stu+1,stu+1+N,cmp);cout<<stu[1].name<<' '<<stu[1].chinese<<' '<<stu[1].math<<' '<<stu[1].eng;return 0;
}输入输出
getchar()获取空字符
scanf读时间/日期
用scanf读要把流关闭
scanf可以按照一定的格式读入数据。读入整数用%d,读入long long 用%lld
printf("%02d\n",a),表示输出2位数字,没有两位就补前导0
题目
日期问题
set、map、priority_queue 等容器在存储自定义结构体时,必须知道如何比较元素(默认按 < 排序)
operator<用于 set 去重和排序:set 会自动根据 < 排序,并保证元素唯一

#include <bits/stdc++.h>
using namespace std;struct Node {int year, month, day;// set对于自定义的结构体,要定义比较运算符,用于排序bool operator<(const Node& other) const {//返回year成员较小的对象为trueif (year != other.year) return year < other.year;//返回month成员较小的对象为trueif (month != other.month) return month < other.month;//返回day成员较小的对象为truereturn day < other.day;}
};bool leap(int year) {return (year % 400 == 0) || (year % 4 == 0 && year % 100 != 0);
}int main() {int x, y, z;//用scanf读取日期scanf("%d/%d/%d", &x, &y, &z);//题目要求不相同的日期,所以去重set<Node> st;int months[] = {-1, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};for (int year = 1960; year <= 2059; year++) {// 每次年份循环时设置2月天数months[2] = leap(year) ? 29 : 28;for (int month = 1; month <= 12; month++) {for (int day = 1; day <= months[month]; day++) {// 检查三种可能的日期格式if ((x == year % 100 && y == month && z == day) ||(x == month && y == day && z == year % 100) ||(x == day && y == month && z == year % 100)) {st.insert({year, month, day});}}}}// 输出结果for (auto i : st) {//02:输出至少两位,不足补0printf("%d-%02d-%02d\n", i.year, i.month, i.day);}return 0;
}航班时间


#include <bits/stdc++.h>
using namespace std;int f(){int h1,h2,m1,m2,s1,s2;scanf("%d:%d:%d %d:%d:%d",&h1,&m1,&s1,&h2,&m2,&s2);int day=0;if(getchar()==' '){scanf("(%d)",&day);}//把去程/回程花费时间变成秒return (day*24*3600+h2*3600+m2*60+s2)-(h1*3600+m1*60+s1);
}int main(){int n;scanf("%d",&n);while(n--){int sec=(f()+f())/2;//一小时3600秒,总的秒/3600=小时//一分钟60秒,总的秒%3600/60=分钟(总的秒%3600就是不超过一个小时的秒数)//总的秒%60=秒(总的秒%60就是不超过一个分钟)printf("%02d:%02d:%02d\n",sec/3600,sec%3600/60,sec%60);}return 0;
}getline(cin,a)获取整行

while(cin>>a[++cnt])全读,忽略空格换行
题目

#include <bits/stdc++.h>
using namespace std;const int NN=110;
int a[NN];
int N;
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);//这个代表行数的N没有用,因为while(cin>>a[++cnt]);跳过空格换行cin>>N;int cnt=0;//一直输入,++cnt,先++,让数组从下标1开始while(cin>>a[++cnt]);sort(a+1,a+cnt+1);int m,n;for(int i=2;i<=cnt;i++){if(a[i]==a[i-1]+2)m=a[i]-1;if(a[i]==a[i-1])n=a[i];}cout<<m<<" "<<n;return 0;
}stl

stack
对于出栈,一定要判断是否为空,如果栈为空,出栈会报错

题目
表达式括号匹配

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);string s;cin>>s;stack<char>st;for(int i=0;i<s.size();i++){if(s[i]=='(')st.push('(');else if(s[i]==')'){//对于出栈,一定要考虑是否为空,如果栈为空,出栈会报错if(st.empty()){cout<<"NO"<<endl;return 0;}st.pop();}}if(st.empty())cout<<"YES"<<endl;else cout<<"NO"<<endl;return 0;
}后缀表达式
洛谷P1449 后缀表达式_哔哩哔哩_bilibili
题目解析
变成树,遍历方式:遍历左子树,然后遍历右子树,最后遍历根节点
遇到数字就压栈,遇到符号就出栈运算,把运算后新的数字入栈,依次循环

代码
#include <bits/stdc++.h>
using namespace std;string s;
stack<int> st;
int l = 0, r = 0;
int main() {ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin>>s;for(int i = 0; i < s.size(); i++) {if(s[i] == '@') break;if(isdigit(s[i])) {l = l * 10 + (s[i] - '0');}else if(s[i] == '.') {st.push(l);l = 0; // 重置临时数字}else if(s[i] == '+' || s[i] == '-' || s[i] == '*' || s[i] == '/') {// 注意顺序:左操作数先出栈l = st.top(); st.pop();r = st.top(); st.pop();if(s[i] == '+') {st.push(l + r);}else if(s[i] == '-') {st.push(r - l); // 注意顺序}else if(s[i] == '*') {st.push(l * r);}else if(s[i] == '/') {st.push(r / l); // 注意顺序}l = 0; // 重置}}cout << st.top();return 0;
}queue
循环问题用队列做比较好
队列先进先出
在循环问题中,最早发现的节点最早被处理
题目
约瑟夫问题

#include <bits/stdc++.h>
using namespace std;int n,m;
queue<int>que;
int cnt=1;int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m;//把元素放入队列for(int i=1;i<=n;i++) que.push(i);while(que.size()){//首元素保存,然后出队int first=que.front();que.pop();if(cnt==m){//到了规定的此处,出队的元素输出cout<<first<<" ";cnt=1;}else{//没有到规定的次数,原本出队的元素入队que.push(first);cnt++;}}return 0;
}赢球票(循环问题用队列)
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'const int NN=110;
int a[NN];
int N;
queue<int>que;int check(int x){queue<int>empty;swap(que,empty);//实现轮转数组for(int i=x;i<=N;i++)que.push(a[i]);//把x后面的数字入队for(int i=1;i<x;i++)que.push(a[i]);//把x前面的数字入队int sum=0,cur=1;while(!que.empty()){int p=que.front();que.pop();if(p==cur){//如果报数和当前值一样,加上sum+=p;cur=1;}else{//不一样,重新入队(入队操作让圆圈的轮转顺序不变)que.push(p);cur++;}if(cur>N)break;}return sum;
}int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>N;for(int i=1;i<=N;i++)cin>>a[i];int ans=0;for(int i=1;i<=N;i++)ans=max(ans,check(i));cout<<ans;return 0;
}priority_queue
优先队列是一种堆
greater,小根堆,从小到大,堆顶是最小的
less,大根堆,从大到小,堆顶是最大的
![]()
题目
合并果子
#include <bits/stdc++.h>
using namespace std;int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n;cin>>n;priority_queue<int,vector<int>,greater<int>>pque;for(int i=1;i<=n;i++){int x;cin>>x;pque.push(x);}int ans=0;//找到大于两堆才进行合并while(pque.size()>1){int t1=pque.top();pque.pop();int t2=pque.top();pque.pop();ans+=t1+t2;pque.push(t1+t2);}cout<<ans;return 0;
}map
BV1Bw9GYBEj8
哈希表是一种通过键直接访问值的数据结构,很多语言的map底层基于哈希表实现。哈希表内部由一个数组构成,这个数组中的每个元素(数组项 )被视为一个 “桶”
std::map 提供了高效的查找操作。可以通过 count 函数快速判断某个键是否存在
find函数,指向键等于 key 的元素的迭代器。若找不到这种元素,则返回尾后(end() )迭代器

map自动按照第一个type的字典序,从小到大排序

哈希表的实现
#include <bits/stdc++.h>
using namespace std;map<int,bool>mp;
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int q;cin>>q;while(q--){char op;int x;cin>>op>>x;if(op=='I')mp[x]=true;else cout<<(mp.count(x)?"Yes":"No")<<endl;}return 0;
}密文搜索

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);string s;cin>>s;map<string,int>mp;for(int i=0;i<s.size();i++){string str=s.substr(i,8);if(str.size()!=8)break;//获得每一个子串,自己按照字典序手动排序sort(str.begin(),str.end());//有相同排序的,就是同一种,直接++mp[str]++;}int n;cin>>n;int ans=0;for(int i=1;i<=n;i++){string str;cin>>str;//对密码列表进行手动排序sort(str.begin(),str.end());//经过排序后,一样的话,加上一样的个数,就是答案ans+=mp[str];}cout<<ans;return 0;
}set


题目
不重复数字(用set存元素,元素顺序存数组,手动按顺序输出)

用set存数字,虽然可以去重,但是会从小到大排序
可以存数组,让set去重之后,按照数组中数字的顺序
通过count和erase手动按照顺序输出
#include <bits/stdc++.h>
using namespace std;int T,n;
const int NN=5e4+10;
int a[NN];void solve(){cin>>n;set<int>st;//这里元素用数组存,应为set会从小到大排序,不能直接存数字for(int i=1;i<=n;i++){cin>>a[i];st.insert(a[i]);}for(int i=1;i<=n;i++){//因为用数组a保存了元素的顺序,让i=1开始遍历,就能按照顺序输出if(st.count(a[i])){//如果存在这个数字,输出,然后删除所有相同的元素cout<<a[i]<<' ';st.erase(a[i]);}}cout<<endl;
}int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>T;while(T--)solve();return 0;
}unordered_set
set有序集合,速度log
unordered_set无序集合,速度c
都是不重复
题目
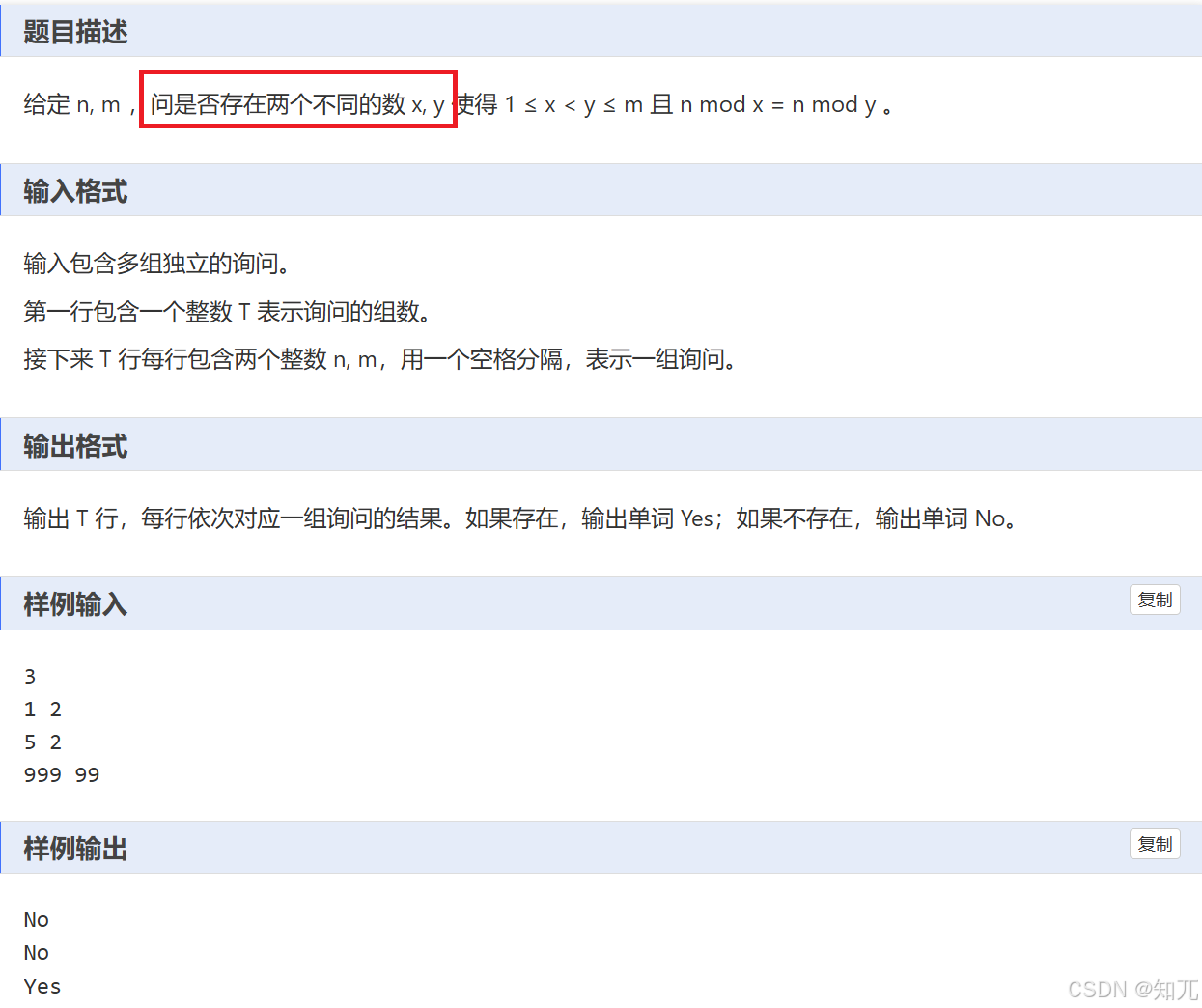
#include <bits/stdc++.h>
using namespace std;
int main(){int tt;scanf("%d",&tt);while(tt--){int n,m;scanf("%d %d",&n,&m);bool flag=false;unordered_set<int>sett;for(int i=1;i<=m;i++){int temp=n%i;auto it=sett.find(temp);if(it!=sett.end()){cout<<"Yes"<<'\n';flag=true;break;}else{sett.insert(temp);}}if(!flag)cout<<"No"<<'\n';}return 0;
}用advance()移动迭代器 (额外)

题目
第k小整数(advance()移动set)

#include <bits/stdc++.h>
using namespace std;int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int n, k;cin >> n >> k;set<int> st;while(n--){int x; cin >> x;st.insert(x);}// 输出第k小的元素if(st.size() < k) {cout << "NO RESULT";} else {auto it = st.begin();advance(it, k-1); // 移动到第k小的元素cout << *it;}return 0;
}双指针
题目
最长子序列
题目解析
一个指针指向S,一个指针指向T
遍历S,如果S[i]==T[j],j++

代码
#include <bits/stdc++.h>
using namespace std;string S,T;
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>S>>T;int ans=0;for(int i=0,j=0;i<S.size()and j<T.size();i++){if(S[i]==T[j]){j++;ans++;}}cout<<ans;return 0;
}#include <bits/stdc++.h>
using namespace std;
#define int long longint a,b,n;
int ans=0;void solve(){cin>>a>>b>>n;int cnt=0;for(int week=1;;week++){week%=7;if(week>=1&&week<=5){cnt+=a;ans++;}else{cnt+=b;ans++;}if(cnt>=n)return;}
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int _=1;while(_--)solve();cout<<ans;return 0;
}几何
拼正方形
要拼成一个正方形,需要的相同的小正方形的个数必须是完全平方数
题目

题目分析
要使边长尽可能的大,就肯定是要多用 2×2 的方块
我们先用 2×2 的方块拼一个最大正方形
的结果2717561.0183988509662675986152793⋯,向下取整后值为 2717561,因为用的是2*2的方块,所以边长要*2(不然就是用1×1小正方形拼成正方形时的边长),目前正方形最大边长就是 2717561×2=5435122
这时,再用1*1的方块补
到这里要想让边长 +1 就要用 5435122×4+4 个 1×1 的正方形
但是5435122×4+4>10470245,故不能再拼一层
答案
5435122
相关文章:

算法(蓝桥杯学习C/C++版)
up: 溶金落梧桐 溶金落梧桐的个人空间-溶金落梧桐个人主页-哔哩哔哩视频 蓝桥杯三十天冲刺系列 BV18eQkY3EtP 网站: OI Wiki OI Wiki - OI Wiki 注意 比赛时,devc勾选c11(必看) 必须勾选c11一共有两个方法,任用…...

Docker镜像无法拉取问题解决办法
最近再学习RabbitMQ,需要从Docker镜像中拉取rabbitMQ,但是下拉失败 总的来说就是无法和docker镜像远程仓库建立连接 我又去尝试ping docker.io发现根本没有反应,还是无法连接找了许多办法还是没有办法解决,最后才发现是镜像问题&a…...

ZephyrOS 嵌入式开发Black Pill V1.2之Debug调试器
版本和环境信息如下: PC平台: Windows 11 专业版 Zephyr开发环境:v4.1.0 Windows 下搭建 Zephyr 开发环境 WeAct BlackPill V1.2开发板: WeAct STM32F411CEU6 BlackPill 核心板 Debug调试器: ST-LINK V2: ST-LINK V2 S…...
:英文越狱提示词下的表现与分析)
# 主流大语言模型安全性测试(二):英文越狱提示词下的表现与分析
主流大语言模型安全性测试(二):英文越狱提示词下的表现与分析 在上一篇文章中,我们对多个主流大语言模型(LLM)进行了中文诱导性提示词的越狱测试,评估其是否能够在面对非法、有害或危险内容请求…...

SAP 在 AI 与数据统一平台上的战略转向
在 2025 年 SAP Sapphire 大会上,SAP 展示了其最新的产品战略和技术整合方向,与以往不同的是,今年的讨论更加务实、聚焦客户实际需求。SAP 强调,ERP 的转型不再是“一刀切”或破坏性的,而是可以根据客户现状࿰…...

服务器磁盘空间被Docker容器日志占满处理方法
事发场景: 原本正常的服务停止运行了,查看时MQTT服务链接失败,查看对应的容器服务发现是EMQX镜像停止运行了,重启也是也报错无法正常运行,报错如下图: 报错日志中连续出现两个"no space left on devi…...

c++学习-this指针
1.基本概念 非静态成员函数都会默认传递this指针(静态成员函数属于类本身,不属于某个实例对象),方便访问对象对类成员变量和 成员函数。 2.基本使用 编译器实际处理类成员函数,this是第一个隐藏的参数,类…...
交易所系统攻坚:高并发撮合引擎与合规化金融架构设计
交易所系统攻坚:高并发撮合引擎与合规化金融架构设计 ——2025年数字资产交易平台的性能与合规双轮驱动 一、高并发撮合引擎:从微秒级延迟到百万TPS 核心架构设计 订单簿优化:数据结构创新:基于红黑树与链表混合存储,…...

OpenCV计算机视觉实战(10)——形态学操作详解
OpenCV计算机视觉实战(10)——形态学操作详解 0. 前言1. 腐蚀与膨胀1.1 为什么要做腐蚀与膨胀1.2 OpenCV 实现 2. 开运算与闭运算2.1 开运算与闭运算原理2.2 OpenCV 实现 3. 形态学梯度与骨架提取3.1 形态学梯度3.2 骨架提取 小结系列链接 0. 前言 形态…...

libiec61850 mms协议异步模式
之前项目中使用到libiec61850库,都是服务端开发。这次新的需求要接收服务端的遥测数据,这就涉及到客户端开发了。 客户端开发没搞过啊,挑战不少,但是人不就是通过战胜困难才成长的嘛。通过查看libiec61850的客户端API发现…...

[论文阅读] 人工智能 | 利用负信号蒸馏:用REDI框架提升LLM推理能力
【论文速读】利用负信号蒸馏:用REDI框架提升LLM推理能力 论文信息 arXiv:2505.24850 cs.LG cs.AI cs.CL Harnessing Negative Signals: Reinforcement Distillation from Teacher Data for LLM Reasoning Authors: Shuyao Xu, Cheng Peng, Jiangxuan Long, Weidi…...

基于 NXP + FPGA+Debian 高可靠性工业控制器解决方案
在工业系统开发中,**“稳定”**往往比“先进”更重要。设备一旦部署,生命周期动辄 5~10 年,系统重启或异常恢复成本高昂。 这时候,一套“值得托付”的软硬件组合,就显得尤为关键。 ✅ NXP —— 提供稳定、长期供货的工…...

CSS 选择器全解析:分组选择器/嵌套选择器,从基础到高级
一、CSS 选择器基础:从单个元素到多个元素 CSS 选择器是用来定位 HTML 元素的工具,就像 “元素的地址”。最基础的选择器有: 元素选择器(按标签名定位) css p { color: red; } /* 所有<p>标签 */ div { b…...

uniapp 对接腾讯云IM群公告功能
UniApp 实战:腾讯云IM群公告功能 一、前言 在即时通讯场景中,群公告是信息同步的重要渠道。本文将基于uniapp框架,结合腾讯云IM SDK,详细讲解如何实现群公告的发布、修改、历史记录查询等核心功能。 群公告的数据结构设计权限校…...

垂起固定翼无人机应用及技术分析
一、主要应用行业 1. 能源基础设施巡检 电力巡检:适用于超高压输电线路通道的快速巡查,实时回传数据提升智能运检效率。 油田管道监测:利用长航时特性(1.5-2小时)对大范围管道进行隐患排查,减少人力巡…...

Python Robot Framework【自动化测试框架】简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

vite配置@别名,以及如何让IDE智能提示路经
1.配置路径(vite.config.js) // vite.config.js import { defineConfig } from "vite"; import vue from "vitejs/plugin-vue"; import path from "path";// https://vite.dev/config/ export default defineConfig({server: {port: 8080,},plu…...

c#bitconverter操作,不同变量类型转byte数组
缘起:串口数据传输的基础是byte数组,write(buff,0,num)或者writeline(string),如果是字符串传输就是string变量就可以了,但是在modbus这类hex传递时,就要遇到转换了,拼凑byte数组时需要各种变量的值传递,解…...
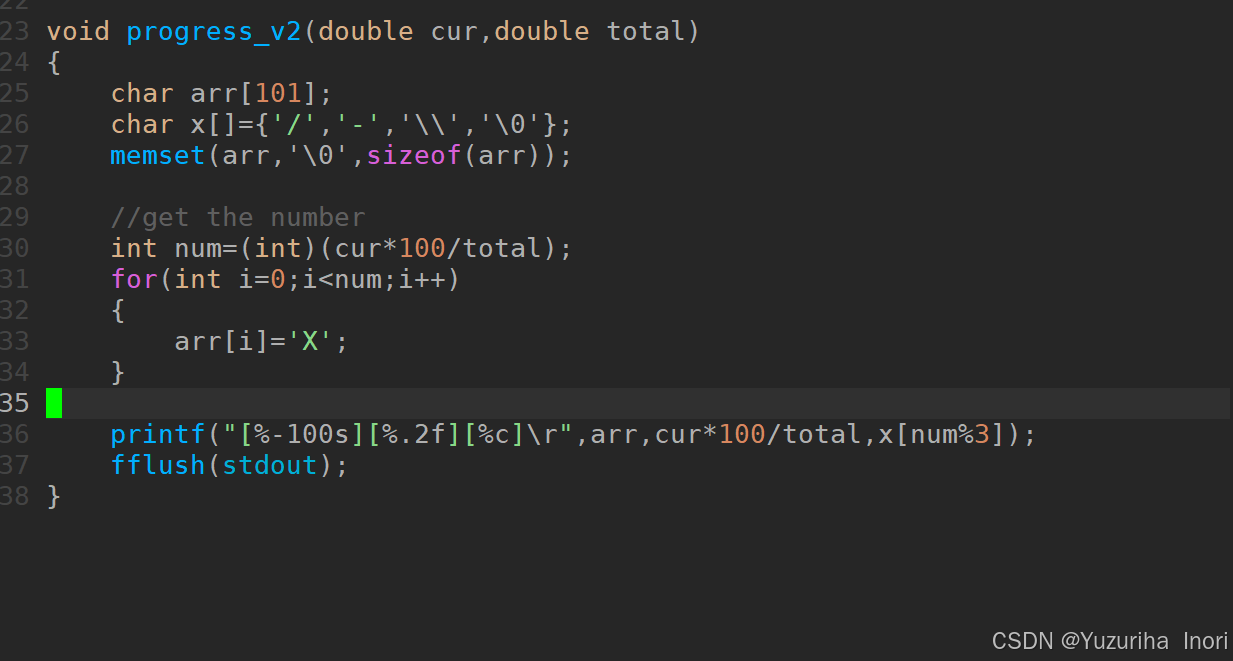
【Linux】LInux下第一个程序:进度条
前言: 在前面的文章中我们学习了LInux的基础指令 【Linux】初见,基础指令-CSDN博客【Linux】初见,基础指令(续)-CSDN博客 学习了vim编辑器【Linux】vim编辑器_linux vim insert-CSDN博客 学习了gcc/g【Linux】编译器gc…...

RPA+AI:自动化办公机器人开发指南
RPAAI:自动化办公机器人开发指南 系统化学习人工智能网站(收藏):https://www.captainbed.cn/flu 文章目录 RPAAI:自动化办公机器人开发指南摘要引言技术融合路径1. 传感器层:多模态数据接入2. 决策层&…...
+ SSS)
daz3d + PBRSkin (MDL)+ SSS
好的,我们来解释一下 Daz3D 中的 PBRSkin (MDL) Shader。 简单来说,PBRSkin (MDL) 是 Daz Studio 中一种基于物理渲染(PBR)技术、专门用于创建高度逼真人物皮肤效果的着色器(Shader)。 它利用 NVIDIA 的材…...
计算矩阵A和B的乘积
根据矩阵乘法规则,编程计算矩阵的乘积。函数fix_prod_ele()是基本方法编写,函数fix_prod_opt()是优化方法编写。 程序代码 #define N 3 #define M 4 typedef int fix_matrix1[N][M]; typedef int fix_matrix2[M][N]; int fix_prod_ele(f…...

Houdini POP入门学习05 - 物理属性
接下来随着教程学习碰撞部分,当粒子较为复杂或者下载了一些粒子模板进行修改时,会遇到一些较奇怪问题,如粒子穿透等,这些问题实际上可以通过调节参数解决。 hip资源文件:https://download.csdn.net/download/grayrail…...

每日Prompt:双重曝光
提示词 新中式,这幅图像将人体头像轮廓与山水中式建筑融为一体,双重曝光,体现了反思、内心平静以及人与自然相互联系的主题,靛蓝,水墨画,晕染,极简...
)
sendDefaultImpl call timeout(rocketmq)
rocketmq 连接异常 senddefaultimpl call timeout-腾讯云开发者社区-腾讯云 第一种情况: 修改broker 的配置如下,注意brokerIP1 这个配置必须有,不然 rocketmq-console 显示依然是内网地址 caused by: org.apache.rocketmq.remoting.excep…...
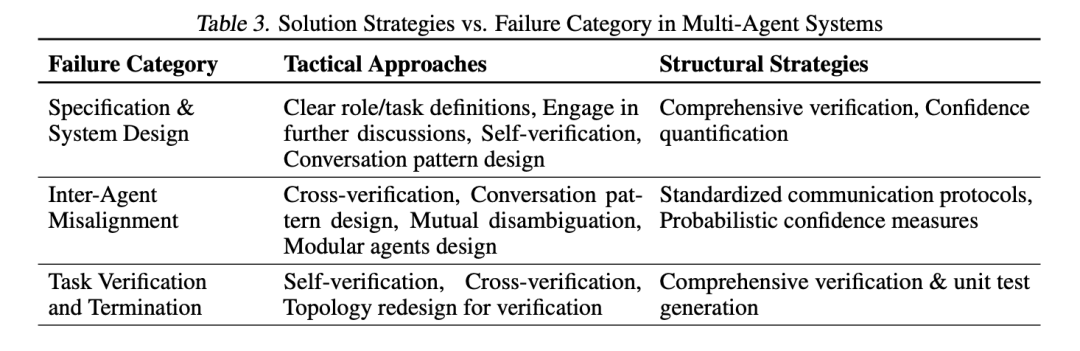
【LLM】多智能体系统 Why Do Multi-Agent LLM Systems Fail?
note 构建一个成功的 MAS,不仅仅是提升底层 LLM 的智能那么简单,它更像是在构建一个组织。如果组织结构、沟通协议、权责分配、质量控制流程设计不当,即使每个成员(智能体)都很“聪明”,整个系统也可能像一…...

CSS 定位:原理 + 场景 + 示例全解析
一. 什么是CSS定位? CSS中的position属性用于设置元素的定位方式,它决定了元素在页面中的"定位行为" 为什么需要定位? 常规布局(如 display: block)适用于主结构 定位适用于浮动按钮,弹出层,粘性标题等场景帮助我们精确控制元素在页面中的位置 二. 定位类型全…...

如何在没有 iTunes 的情况下备份 iPhone
我可以在没有 iTunes 的情况下将 iPhone 备份到电脑吗?虽然 iTunes 曾经是备份 iPhone 的主要方法,但它并不是 iOS 用户唯一的备份选项。您可以选择多种方便的替代方案来备份 iPhone,无需使用 iTunes。您可以在这里获得更灵活、更人性化的备份…...
如何把 Mac Finder 用得更顺手?——高效文件管理定制指南
系统梳理提升 Mac Finder 体验的实用设置与技巧,助你用更高效的方式管理文件。文末引出进阶选择 Path Finder。 阅读原文请转到:https://jimmysong.io/blog/customize-finder-for-efficiency/ 作为一个用 Mac 多年的用户,我始终觉得 Finder 虽…...

赋能大型语言模型与外部世界交互——函数调用的崛起
大型语言模型 (LLM) 近年来在自然语言处理领域取得了革命性的进展,展现出强大的文本理解、生成和对话能力。然而,这些模型在与外部实时数据源和动态系统交互方面存在固有的局限性 1。它们主要依赖于训练阶段学习到的静态知识,难以直接访问和利…...