求解插值多项式及其余项表达式
例
求满足 P ( x j ) = f ( x j ) P(x_j) = f(x_j) P(xj)=f(xj) ( j = 0 , 1 , 2 j=0,1,2 j=0,1,2) 及 P ′ ( x 1 ) = f ′ ( x 1 ) P'(x_1) = f'(x_1) P′(x1)=f′(x1) 的插值多项式及其余项表达式。
解:
由给定条件,可确定次数不超过3的插值多项式。此多项式通过点 ( x 0 , f ( x 0 ) ) , ( x 1 , f ( x 1 ) ) (x_0,f(x_0)),(x_1,f(x_1)) (x0,f(x0)),(x1,f(x1))及 ( x 2 , f ( x 2 ) ) (x_2,f(x_2)) (x2,f(x2)),故形式为
P ( x ) = f ( x 0 ) + f [ x 0 , x 1 ] ( x − x 0 ) + f [ x 0 , x 1 , x 2 ] ( x − x 0 ) ( x − x 1 ) + A ( x − x 0 ) ( x − x 1 ) ( x − x 2 ) P(x) = f(x_0) + f[x_0,x_1](x-x_0) + f[x_0,x_1,x_2](x-x_0)(x-x_1)+ A(x-x_0)(x-x_1)(x-x_2) P(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+A(x−x0)(x−x1)(x−x2),
其中A为待定常数,可由条件 P ′ ( x 1 ) = f ′ ( x 1 ) P'(x_1) = f'(x_1) P′(x1)=f′(x1)确定
A = f ′ ( x 1 ) − f [ x 0 , x 1 ] − ( x 1 − x 0 ) f [ x 0 , x 1 , x 2 ] ( x 1 − x 0 ) ( x 1 − x 2 ) A=\frac{f'(x_1)-f[x_0,x_1]-(x_1-x_0)f[x_0,x_1,x_2]}{(x_1-x_0)(x_1-x_2)} A=(x1−x0)(x1−x2)f′(x1)−f[x0,x1]−(x1−x0)f[x0,x1,x2]
为求出余项 R ( x ) = f ( x ) − P ( x ) R(x)=f(x)-P(x) R(x)=f(x)−P(x)的表达式,设
R ( x ) = f ( x ) − P ( x ) = K ( x ) ( x − x 0 ) 2 ( x − x 1 ) 2 ( x − x 2 ) R(x) = f(x)-P(x) = K(x)(x-x_0)^2(x-x_1)^2(x-x_2) R(x)=f(x)−P(x)=K(x)(x−x0)2(x−x1)2(x−x2)
其中 K ( x ) K(x) K(x)为待定函数。
构造
φ ( t ) = f ( t ) − P ( t ) − K ( x ) ( t − x 0 ) 2 ( t − x 1 ) 2 ( t − x 2 ) \varphi(t) = f(t)-P(t)-K(x)(t-x_0)^2(t-x_1)^2(t-x_2) φ(t)=f(t)−P(t)−K(x)(t−x0)2(t−x1)2(t−x2)
显然 φ ( x j ) = 0 ( j = 0 , 1 , 2 ) \varphi(x_j)=0(j=0,1,2) φ(xj)=0(j=0,1,2),且 φ ′ ( x 1 ) = 0 , φ ( x ) = 0 \varphi'(x_1)=0,\varphi(x)=0 φ′(x1)=0,φ(x)=0,故 φ ( t ) \varphi(t) φ(t)在 ( a , b ) (a,b) (a,b)内有五个零点(重根算两个)。
由Rolle 定理, φ ( 4 ) ( t ) \varphi^{(4)}(t) φ(4)(t)在 ( a , b ) (a,b) (a,b)内至少有一个零点 ξ \xi ξ,故
φ ( 4 ) ( ξ ) = f ( 4 ) ( ξ ) − 4 ! K ( x ) = 0 \varphi^{(4)}(\xi)=f^{(4)}(\xi)-4!K(x)=0 φ(4)(ξ)=f(4)(ξ)−4!K(x)=0
于是 K ( x ) = f ( 4 ) ( ξ ) / 4 ! K(x)=f^{(4)}(\xi)/4! K(x)=f(4)(ξ)/4!,余项表达式为
R ( x ) = f ( 4 ) ( ξ ) ( x − x 0 ) ( x − x 1 ) 2 ( x − x 2 ) / 4 ! R(x)=f^{(4)}(\xi)(x-x_0)(x-x_1)^2(x-x_2)/4! R(x)=f(4)(ξ)(x−x0)(x−x1)2(x−x2)/4!
其中 ξ \xi ξ位于 x 0 , x 1 , x 2 x_0,x_1,x_2 x0,x1,x2和 x x x所界定的范围内.
相关文章:

求解插值多项式及其余项表达式
例 求满足 P ( x j ) f ( x j ) P(x_j) f(x_j) P(xj)f(xj) ( j 0 , 1 , 2 j0,1,2 j0,1,2) 及 P ′ ( x 1 ) f ′ ( x 1 ) P(x_1) f(x_1) P′(x1)f′(x1) 的插值多项式及其余项表达式。 解: 由给定条件,可确定次数不超过3的插值多项式。…...

vue3: bingmap using typescript
项目结构: <template><div class"bing-map-market"><!-- 加载遮罩层 --><div class"loading-overlay" v-show"isLoading || errorMessage"><div class"spinner-container"><div class&qu…...

vue3前端实现导出Excel功能
前端实现导出功能可以使用一些插件 我使用的是xlsx库 1.首先我们需要在vue3的项目中安装xlsx库。可以使用npm 或者 pnpm来进行安装 npm install xlsx或者 pnpm install xlsx2.在vue组件中引入xlsx库 import * as XLSX from xlsx;3.定义导出实例方法 const exportExcel () …...

超大规模芯片验证:基于AMD VP1902的S8-100原型验证系统实测性能翻倍
引言: 随着AI、HPC及超大规模芯片设计需求呈指数级增长原型验证平台已成为芯片设计流程中验证复杂架构、缩短迭代周期的核心工具。然而,传统原型验证系统受限于单芯片容量(通常<5000万门)、多芯片分割效率及系统级联能力&#…...

【工作记录】接口功能测试总结
如何对1个接口进行接口测试 一、单接口功能测试 1、接口文档信息 理解接口文档的内容: 请求URL: https://[ip]:[port]/xxxserviceValidation 请求方法: POST 请求参数: serviceCode(必填), servicePsw(必填) 响应参数: status, token 2、编写测试用例 2.1 正…...

Dubbo Logback 远程调用携带traceid
背景 A项目有调用B项目的服务,A项目使用 logback 且有 MDC 方式做 traceid,调用B项目的时候,traceid 没传递过期,导致有时候不好排查问题和链路追踪 准备工作 因为使用的是 alibaba 的 dubbo 所以需要加入单独的包 <depend…...

【element-ui】el-autocomplete实现 无数据匹配
文章目录 方法一:使用 default 插槽方法二:使用 empty-text 属性(适用于列表类型)总结 在使用 Element UI 的 el-autocomplete 组件时,如果你希望在没有任何数据匹配的情况下显示特定的内容,你可以通过自定…...

NLP学习路线图(二十):FastText
在自然语言处理(NLP)领域,词向量(Word Embedding)是基石般的存在。它将离散的符号——词语——转化为连续的、富含语义信息的向量表示,使得计算机能够“理解”语言。而在众多词向量模型中,FastText 凭借其独特的设计理念和卓越性能,尤其是在处理形态丰富的语言和罕见词…...

力扣面试150题--除法求值
Day 62 题目描述 做法 此题本质是一个图论问题,对于两个字母相除是否存在值,其实就是判断,从一个字母能否通过其他字母到达,做法如下: 遍历所有等式,为每个变量分配唯一的整数索引。初始化一个二维数组 …...

SQL进阶之旅 Day 20:锁与并发控制技巧
【JDK21深度解密 Day 20】锁与并发控制技巧 文章简述 在高并发的数据库环境中,锁与并发控制是保障数据一致性和系统稳定性的核心机制。本文作为“SQL进阶之旅”系列的第20天,深入探讨SQL中的锁机制、事务隔离级别以及并发控制策略。文章从理论基础入手…...

美业破局:AI智能体如何用数据重塑战略决策(5/6)
摘要:文章深入剖析美业现状与挑战,指出其市场规模庞大但竞争激烈,面临获客难、成本高、服务标准化缺失等问题。随后阐述 AI 智能体与数据驱动决策的概念,强调其在美业管理中的重要性。接着详细说明 AI 智能体在美业数据收集、整理…...
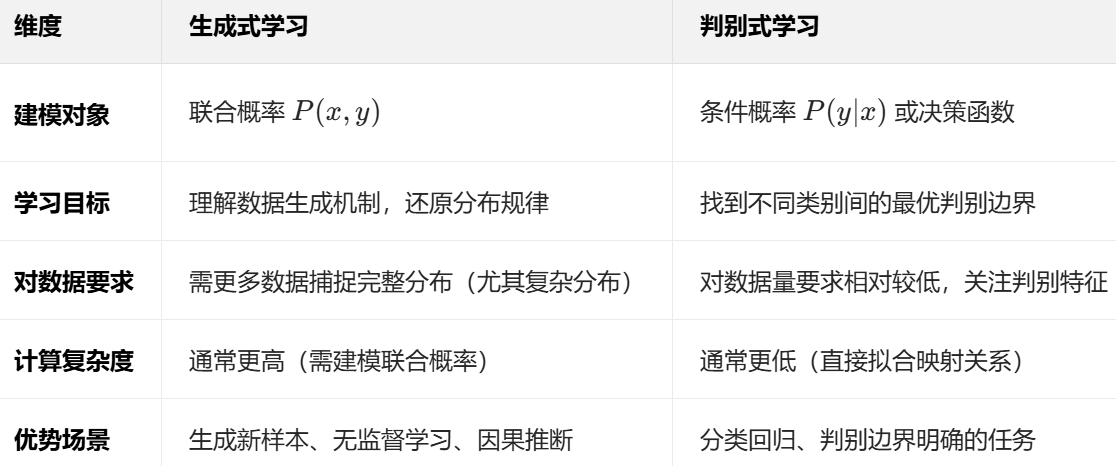
生成模型+两种机器学习范式
生成模型:从数据分布到样本创造 生成模型(Generative Model) 是机器学习中一类能够学习数据整体概率分布,并生成新样本的模型。其核心目标是建模输入数据 x 和标签 y 的联合概率分布 P(x,y),即回答 “数据是如何产生的…...

【学习笔记】Python金融基础
Python金融入门 1. 加载数据与可视化1.1. 加载数据1.2. 折线图1.3. 重采样1.4. K线图 / 蜡烛图1.5. 挑战1 2. 计算2.1. 收益 / 回报2.2. 绘制收益图2.3. 累积收益2.4. 波动率2.5. 挑战2 3. 滚动窗口3.1. 创建移动平均线3.2. 绘制移动平均线3.3 Challenge 4. 技术分析4.1. OBV4.…...

在Linux查看电脑的GPU型号
VGA 是指 Video Graphics Array,这是 IBM 于 1987 年推出的一种视频显示标准。 lspci | grep vga 📌 lspci | grep -i vga 的含义 lspci:列出所有连接到 PCI 总线的设备。 grep -i vga:过滤输出,仅显示包含“VGA”字…...

A Execllent Software Project Review and Solutions
The Phoenix Projec: how do we produce software? how many steps? how many people? how much money? you will get it. i am a pretty judge of people…a prank...

windows命令行面板升级Git版本
Date: 2025-06-05 11:41:56 author: lijianzhan Git 是一个 分布式版本控制系统 (DVCS),由 Linux 之父 Linus Torvalds 于 2005 年开发,用于管理 Linux 内核开发。它彻底改变了代码协作和版本管理的方式,现已成为软件开发的事实标准工具&…...

Langgraph实战--自定义embeding
概述 在Langgraph中我想使用第三方的embeding接口来实现文本的embeding。但目前langchain只提供了两个类,一个是AzureOpenAIEmbeddings,一个是:OpenAIEmbeddings。通过ChatOpenAI无法使用第三方的接口,例如:硅基流平台…...

大故障,阿里云核心域名疑似被劫持
2025年6月5日凌晨,阿里云多个服务突发异常,罪魁祸首居然是它自家的“核心域名”——aliyuncs.com。包括对象存储 OSS、内容分发 CDN、镜像仓库 ACR、云解析 DNS 等服务在内,全部受到波及,用户业务连夜“塌房”。 更让人惊讶的是&…...
)
什么是「镜像」?(Docker Image)
🧊 什么是「镜像」?(Docker Image) 💡 人话解释: Docker 镜像就像是一个装好程序的“快照包”,里面包含了程序本体、依赖库、运行环境,甚至是系统文件。 你可以把镜像理解为&…...

SQLMesh实战:用虚拟数据环境和自动化测试重新定义数据工程
在数据工程领域,软件工程实践(如版本控制、测试、CI/CD)的引入已成为趋势。尽管像 dbt 这样的工具已经推动了数据建模的标准化,但在测试自动化、工作流管理等方面仍存在不足。 SQLMesh 应运而生,旨在填补这些空白&…...

服务器健康摩尔斯电码:深度解读S0-S5状态指示灯
当服务器机柜中闪烁起神秘的琥珀色灯光,运维人员的神经瞬间绷紧——这些看似简单的Sx指示灯,实则是服务器用硬件语言发出的求救信号。掌握这套"摩尔斯电码",等于拥有了预判故障的透视眼。 一、状态指示灯:服务器的生命体…...

设计模式基础概念(行为模式):模板方法模式 (Template Method)
概述 模板方法模式是一种行为设计模式, 它在超类中定义了一个算法的框架, 允许子类在不修改结构的情况下重写算法的特定步骤。 是基于继承的代码复用的基本技术,模板方法模式的类结构图中,只有继承关系。 需要开发抽象类和具体子…...
传统业务对接AI-AI编程框架-Rasa的业务应用实战(番外篇2)-- Rasa 训练数据文件的清理
经过我的【传统业务对接AI-AI编程框架-Rasa的业务应用实战】系列 1-6 的表述 已经实现了最初的目标:将传统平台业务(如发票开具、审核、计税、回款等)与智能交互结合,通过用户输入提示词或语音,识别用户意图和实体信…...

LVDS的几个关键电压概念
LVDS的几个关键电压概念 1.LVDS的直流偏置 直流偏置指的是信号的电压围绕的基准电压,信号的中心电压。在LVDS中,信号是差分的, 两根线之间的电压差表示数据,很多时候两根线的电压不是在0v开始变化的,而是在某个 固定的…...

2023年ASOC SCI2区TOP,随机跟随蚁群优化算法RFACO,深度解析+性能实测
目录 1.摘要2.连续蚁群优化算法ACOR3.随机跟随策略4.结果展示5.参考文献6.代码获取7.算法辅导应用定制读者交流 1.摘要 连续蚁群优化是一种基于群体的启发式搜索算法(ACOR),其灵感来源于蚁群的路径寻找行为,具有结构简单、控制参…...
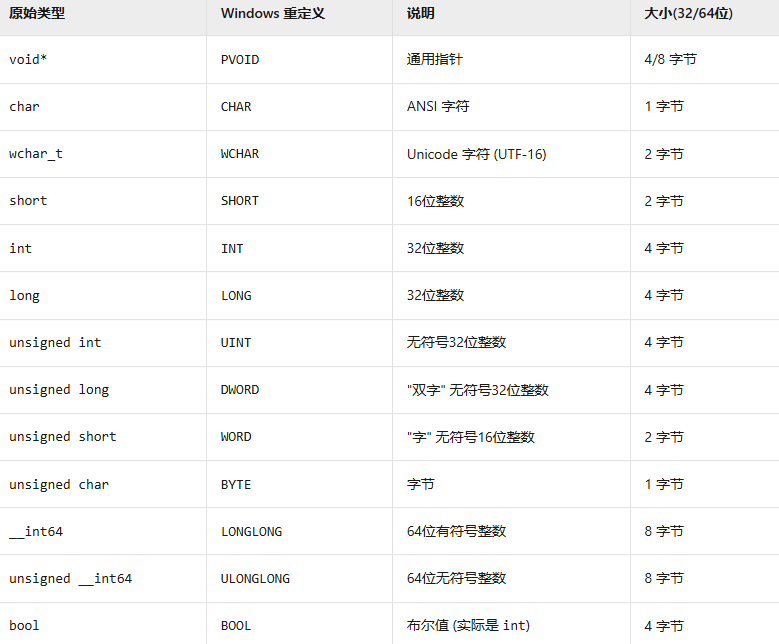
DLL动态库实现文件遍历功能(Windows编程)
源文件: 文件遍历功能的动态库,并支持用户注册回调函数处理遍历到的文件 a8f80ba 周不才/cpp_linux study - Gitee.com 知识准备 1.Windows中的数据类型 2.DLL导出/导入宏 使用__declspec(dllexport)修饰函数,将函数标记为导出函数存放到…...

Java Map完全指南:从基础到高级应用
文章目录 1. Map接口概述Map的基本特性 2. Map接口的核心方法基本操作方法批量操作方法 3. 主要实现类详解3.1 HashMap3.2 LinkedHashMap3.3 TreeMap3.4 ConcurrentHashMap 4. 高级特性和方法4.1 JDK 1.8新增方法4.2 Stream API结合使用 5. 性能比较和选择建议性能对比表选择建…...

jvm 垃圾收集算法 详解
垃圾收集算法 分代收集理论 垃圾收集器的理论基础,它建立在两个分代假说之上: 弱分代假说:绝大多数对象都是朝生夕灭的。强分代假说:熬过越多次垃圾收集过程的对象就越难以消亡。 这两个分代假说共同奠定了多款常用的垃圾收集…...

[特殊字符] 深入理解 Linux 内核进程管理:架构、核心函数与调度机制
Linux 内核作为一个多任务操作系统,其进程管理子系统是核心组成部分之一。无论是用户应用的运行、驱动行为的触发,还是系统调度决策,几乎所有操作都离不开进程的创建、调度与销毁。本文将从进程的概念出发,深入探讨 Linux 内核中进…...

Nginx Stream 层连接数限流实战ngx_stream_limit_conn_module
1.为什么需要连接数限流? 数据库/Redis/MQ 连接耗资源:恶意脚本或误配可能瞬间占满连接池,拖垮后端。防御慢速攻击:层叠式限速(连接数+带宽)可阻挡「Slow Loris」之类的 TCP 低速洪水。公平接入…...
