.Net Framework 4/C# 泛型的使用、迭代器和分部类
一、泛型的使用
泛型是用于处理算法、数据结构的一种编程方法。泛型的目标是采用广泛适用和可交互性的形式来表示算法和数据结构,以便它们能够直接用于软件构造。
泛型简单理解就是,在声明时暂时不固定其类型,例如 int 类型、double 类型等,在调用泛型时,再将要用的类型补上。
(一) 类型参数 T
泛型的类型参数 T 可以看作是一个占位符,它不是一种类型,它仅代表了某种可能的类型,类型参数 T 可以在使用时用任何类型来代替。类型参数 T 的命名规则如下:
- 使用描述性名称命名泛型类型参数,除非单个字母名称完全可以让人理解它表示的含义,而描述名称不会有更多的意义;
例如有:
public interface ISessionChannel<Session>
public delegate TOutput Converter<Input, Output>2. T 作为描述性类型参数名的前缀
例如有:
public interface ISessionChannel<TSession>
{TSession Session{ get; }
}(二) 泛型接口
泛型接口的声明形式如下:
<
相关文章:

.Net Framework 4/C# 泛型的使用、迭代器和分部类
一、泛型的使用 泛型是用于处理算法、数据结构的一种编程方法。泛型的目标是采用广泛适用和可交互性的形式来表示算法和数据结构,以便它们能够直接用于软件构造。 泛型简单理解就是,在声明时暂时不固定其类型,例如 int 类型、double 类型等,在调用泛型时,再将要用的类型补…...

LLM 笔记:Speculative Decoding 投机采样
1 基本介绍 投机采样(Speculative Sampling)是一种并行预测多个可能输出,然后快速验证并采纳正确部分的加速策略 在不牺牲输出质量的前提下,减少语言模型生成 token 所需的时间 传统的语言模型生成是 串行 的 必须生成一个&…...

当SAP系统内计划订单转换为生产订单时发生了什么?
【SAP系统研究】 #SAP #计划订单 #生产订单 #采购申请 一、关于计划订单的一点疑惑 曾经对SAP为什么会有计划订单,是感到很疑惑的。 这个界面简单,配置点也不多,能被随意“摆布”,一旦要变形就消失得无影无踪的计划订单,why? 但是,再次重新审视过之后,才发现它其实…...

PDF转PPT转换方法总结
你是否遇到过这些场景? 收到客户发来的产品手册PDF,明天就要用它做演示; 公司历史资料只有PDF版,领导突然要求更新为幻灯片。 这时PDF转PPT工具就成了救命稻草。接下来,介绍三种PDF转PPT工具。 1. iLoveOFD在线转换…...
3D Web轻量化引擎HOOPS Communicator的定制化能力全面解析
HOOPS Communicator 是Tech Soft 3D推出的高性能Web工程图形引擎。它通过功能丰富的JavaScript API,帮助开发团队在浏览器中快速添加2D/3D CAD模型的查看与交互功能。该引擎专为工程应用优化,支持大规模模型的流畅浏览、复杂装配的智能导航、流式加载和服…...
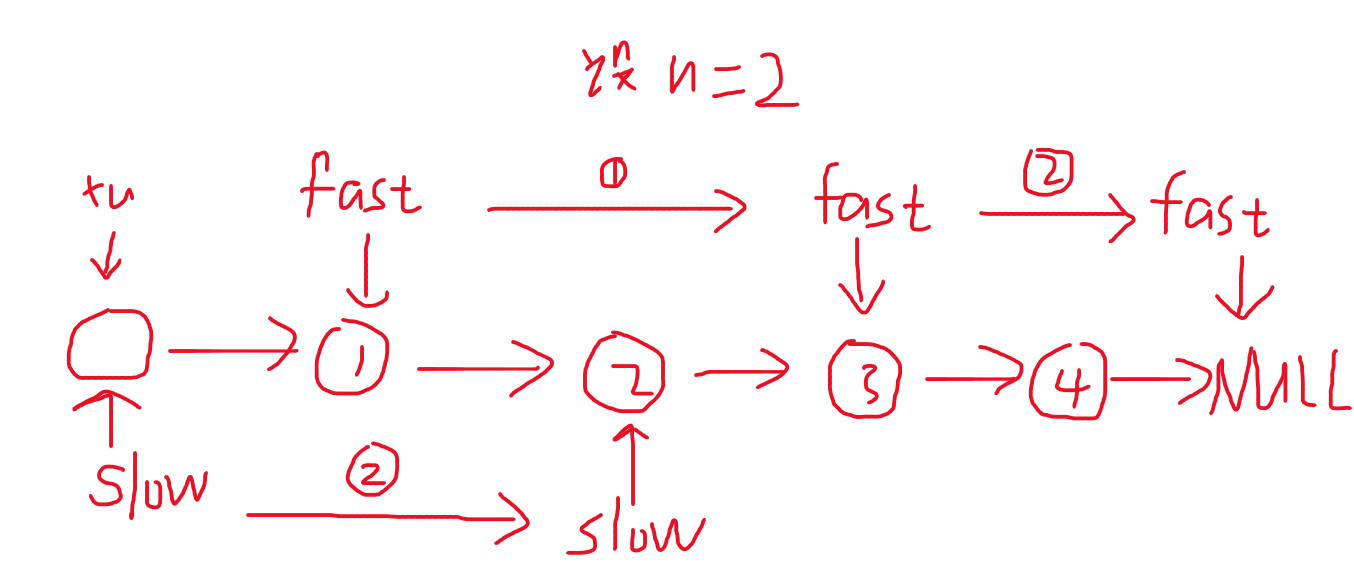
【力扣链表篇】19.删除链表的倒数第N个节点
题目: 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 示例 1: 输入:head [1,2,3,4,5], n 2 输出:[1,2,3,5]示例 2: 输入:head [1], n 1 输出:[]…...

.Net Framework 4/C# 集合和索引器
一、ArrayList 类(集合) ArrayList 类位于 System.Collections 命名空间下,它可以动态地添加和删除元素。 ArrayList 提供了3个构造器,通过这3个构造器可以有3种声明方式: 默认构造器,将会以默认ÿ…...

如何使用Jmeter进行压力测试?
🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 一、什么是压力测试 软件测试中:压力测试(Stress Test),也称为强度测试、负载测试。压力测试是模拟实际应用的软硬…...

Grafana-ECharts应用讲解(玫瑰图示例)
工具: MySQL 数据库 MySQL Workbench 数据库管理工具(方便编辑数据) Grafana v11.5.2 Business Charts 6.6(原 Echarts插件) 安装 安装 MySQL社区版安装 MySQL Workbench安装 Grafana在 Grafana 插件中搜索 Business Charts 进行安装以上安装步骤网上教程很多,自行搜…...

洛谷P1591阶乘数码
P1591 阶乘数码 题目描述 求 n ! n! n! 中某个数码出现的次数。 输入格式 第一行为 t ( t ≤ 10 ) t(t \leq 10) t(t≤10),表示数据组数。接下来 t t t 行,每行一个正整数 n ( n ≤ 1000 ) n(n \leq 1000) n(n≤1000) 和数码 a a a。 输出格式…...

前端vue3 上传/导入文件 调用接口
点击按钮导入: <el-uploadaction"https://run.mocky.io/v3/9d059bf9-4660-45f2-925d-ce80ad6c4d15":auto-upload"false":on-change"handleFileChange":show-file-list"false"><el-button type"warning"…...

概述侧边导航的作用与价值
侧边导航的作用与价值:介绍侧边导航的核心优势和用户体验提升点。设计原则:使用表格对比说明侧边导航的三大设计准则。基础实现方法:分步骤讲解静态侧边导航的实现技术。高级交互实现:提供滑动式侧边栏的完整交互解决方案。优化技…...

Python训练营-Day22-Titanic - Machine Learning from Disaster
Description linkkeyboard_arrow_up 👋🛳️ Ahoy, welcome to Kaggle! You’re in the right place. This is the legendary Titanic ML competition – the best, first challenge for you to dive into ML competitions and familiarize yourself w…...
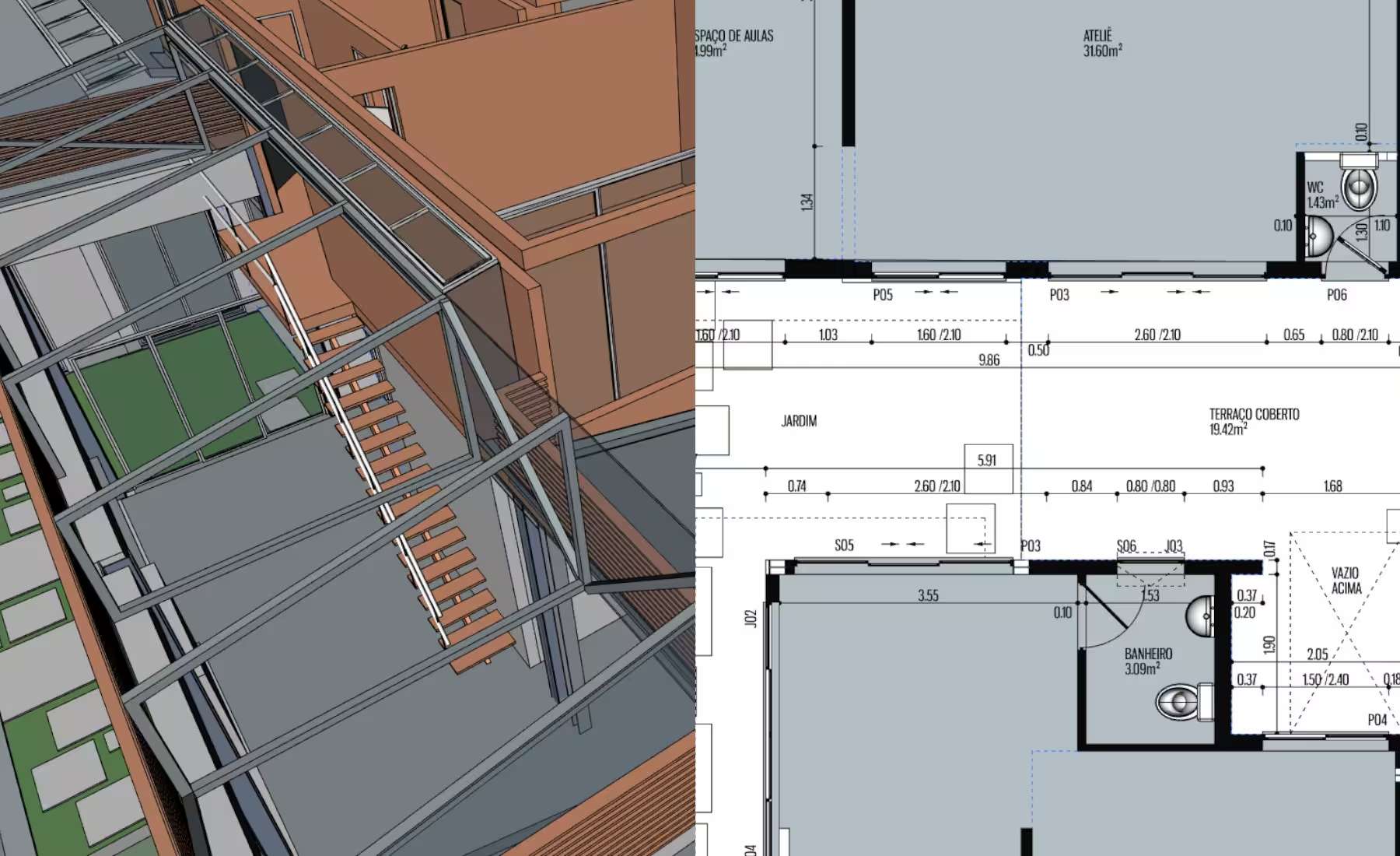
FreeCAD:开源世界的三维建模利器
FreeCAD 开发模式 FreeCAD的开发采用多语言协作模式,其核心框架与高性能模块主要使用C构建,而用户界面与扩展功能则通过Python脚本实现灵活定制。具体来说: C核心层:作为基础架构,C负责实现与Open CASCADE Technology…...

指针的定义与使用
1.指针的定义和使用 int point1(){//定义指针int a 10;//指针定义语法: 数据类型 * 指针变量名int * p;cout << "sizeof (int(*)) --> " << sizeof(p) << endl;//让指针记录变量a的地址 & 取址符p &a ;cout << &qu…...

嵌入式里的时间魔法:RTC 与 BKP 深度拆解
文章目录 RTC实时时钟与BKPUnix时间戳UTC/GMT时间戳转换时间戳转换BKP简介BKP基本结构1. 电池供电模块(VBAT 输入)2. 侵入检测模块(TAMPER 输入)3. 时钟输出模块(RTC 输出)4. 内部寄存器组 RTC简介RTC时钟源…...

Java项目中常用的中间件及其高频问题避坑
Java项目中常用的中间件及其高频问题避坑如下: 一、常用中间件分类及作用 1. 消息队列中间件 作用:解耦系统、异步通信、削峰填谷。代表产品: Kafka:高吞吐量流处理,适合日志收集、实时分析。RocketMQ:金融级可靠性,支持事务消…...

图卷积网络:从理论到实践
图卷积网络(Graph Convolutional Networks, GCNs)彻底改变了基于图的机器学习领域,使得深度学习能够应用于非欧几里得结构,如社交网络、引文网络和分子结构。本文将解释GCN的直观理解、数学原理,并提供代码片段帮助您理…...

ES 学习总结一 基础内容
ElasticSearch学习 一、 初识ES1、 认识与安装2、 倒排索引2.1 正向索引2.2 倒排索引 3、 基本概念3.1 文档和字段3.2 索引和倒排 4 、 IK分词器 二、 操作1、 mapping 映射属性2、 索引库增删改查3、 文档的增删改查3.1 新增文档3.2 查询文档3.3 删除文档3.4 修改文档3.5 批处…...

Maven 构建缓存与离线模式
🧑 博主简介:CSDN博客专家,历代文学网(PC端可以访问:https://literature.sinhy.com/#/?__c=1000,移动端可微信小程序搜索“历代文学”)总架构师,15年工作经验,精通Java编程,高并发设计,Springboot和微服务,熟悉Linux,ESXI虚拟化以及云原生Docker和K8s,热衷于探…...

基于51单片机的光强控制LED灯亮灭
目录 具体实现功能 设计介绍 资料内容 全部内容 资料获取 具体实现功能 具体功能: (1)按下按键K后光敏电阻进行光照检测,LCD1602显示光照强度值; (2)光照值小于15时,上面2个LE…...

【Linux操作系统】基础开发工具(yum、vim、gcc/g++)
文章目录 Linux软件包管理器 - yumLinux下的三种安装方式什么是软件包认识Yum与RPMyum常用指令更新软件安装与卸载查找与搜索清理缓存与重建元数据 yum源更新1. 备份现有的 yum 源配置2. 下载新的 repo 文件3. 清理并重建缓存 Linux编辑器 - vim启动vimVim 的三种主要模式常用操…...

gopool 源码分析
gopool gopool是字节跳动开源节流的gopkg包中协程池的一个实现。 关键结构 协程池: type pool struct {// The name of the poolname string// capacity of the pool, the maximum number of goroutines that are actually working// 协程池的最大容量cap int32…...

【Survival Analysis】【机器学习】【3】 SHAP可解釋 AI
前言: SHAP(SHapley Additive explanations) 是一种基于博弈论的可解释工具。 现在很多高分的 论文里面都会带这种基于SHAP 分析的图,用于评估机器学习模型中特征对预测结果的贡献度. pip install -i https://pypi.tuna.tsinghua.edu.cn/sim…...

ModuleNotFoundError No module named ‘torch_geometric‘未找到
ModuleNotFoundError: No module named torch_geometric’未找到 试了很多方法,都没成功,安装torch对应版本的torch_geometric都不行, 后来发现是pip被设置了环境变量,所有pip文件都给安装在了一个文件夹了 排查建议 1. 检查 p…...

iOS 门店营收表格功能的实现
iOS 门店营收表格功能实现方案 核心功能需求 数据展示:表格形式展示门店/日期维度的营收数据排序功能:支持按营收金额、增长率等排序筛选功能:按日期范围/门店/区域筛选交互操作:点击查看详情、数据刷新数据可视化:关…...

链表题解——环形链表【LeetCode】
141. 环形链表 方法一 核心思想: 使用一个集合 seen 来记录已经访问过的节点。遍历链表,如果当前节点已经存在于集合中,说明链表存在环;否则,将当前节点添加到集合中,继续遍历。如果遍历结束(h…...

Cell-o1:强化学习训练LLM解决单细胞推理问题
细胞类型注释是分析scRNA-seq数据异质性的关键任务。尽管最近的基础模型实现了这一过程的自动化,但它们通常独立注释细胞,未考虑批次水平的细胞背景或提供解释性推理。相比之下,人类专家常基于领域知识为不同细胞簇注释不同的细胞类型。为模拟…...

求解插值多项式及其余项表达式
例 求满足 P ( x j ) f ( x j ) P(x_j) f(x_j) P(xj)f(xj) ( j 0 , 1 , 2 j0,1,2 j0,1,2) 及 P ′ ( x 1 ) f ′ ( x 1 ) P(x_1) f(x_1) P′(x1)f′(x1) 的插值多项式及其余项表达式。 解: 由给定条件,可确定次数不超过3的插值多项式。…...

vue3: bingmap using typescript
项目结构: <template><div class"bing-map-market"><!-- 加载遮罩层 --><div class"loading-overlay" v-show"isLoading || errorMessage"><div class"spinner-container"><div class&qu…...
