FPGA定点和浮点数学运算-实例对比
在创建 RTL 示例时,经常使用 VHDL 2008 附带的 VHDL 包。它提供了出色的功能,可以高效地处理定点数,当然,它们也是可综合的。该包的一些优点包括:
有符号和无符号(后缀和后缀)定点向量。
轻松将定点数表示并量化为定点向量。
小数点位于向量元素 0 和 -1 之间。这样就无需在运算过程中跟踪小数点以进行对齐(大量运算这点很难把握)。
运算的溢出、舍入和范围管理有明确的定义。
算术和比较运算符。
因此,当需要实现算法时,我会使用这个包。但是实际应用时,还会有很多浮点运算。
自然而然地,一个问题出现了:用定点和浮点实现同一个方程时,资源有什么区别?
我们将要看的例子是如何利用多项式近似地将ADC读数转换为温度值。这在工业应用中很常见(使用铂电阻温度计时)。

要实现的具体方程是 y = 2E-09x4 - 4E-07x3 + 0.011x2 + 2.403x - 251.26,该方程是从绘制方程式中提取出来的。虽然我们可以直接实现该方程,但这会非常浪费资源,还会增加开发的复杂性和风险。

使用定点数系统,我们需要做一些量化来保持精度和准确度。
代码和一个简单的仿真如下。
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use ieee.fixed_pkg.all;
entity complex_example is port(
clk : in std_logic;
ip : in std_logic_vector(7 downto 0);
op : out std_logic_vector(8 downto 0));
end complex_example;
architecture Behavioral of complex_example is
signal power_a : sfixed(8 downto -32):=(others=>'0');
signal power_b : sfixed(8 downto -32):=(others=>'0');
signal power_c : sfixed(8 downto -32):=(others=>'0');
signal calc : sfixed(8 downto -32) :=(others=>'0');
signal store : sfixed(8 downto 0) := (others =>'0');
constant a : sfixed(8 downto -32):= to_sfixed( 2.00E-09, 8,-32 );
constant b : sfixed(8 downto -32):= to_sfixed( 4.00E-07, 8,-32 );
constant c : sfixed(8 downto -32):= to_sfixed( 0.0011, 8,-32 );
constant d : sfixed(8 downto -32):= to_sfixed( 2.403, 8,-32 );
constant e : sfixed(8 downto -32):= to_sfixed( 251.26, 8,-32 );
type reg_array is array (9 downto 0) of sfixed(8 downto -32);
signal pipeline_reg : reg_array;
begin
cvd : process(clk)
begin if rising_edge(clk) then store <= to_sfixed('0'&ip,store);power_a <= resize (arg => power_b * store * a,size_res => power_a);power_b <= resize (arg => power_c * store * b,size_res => power_b); power_c <= resize (arg => store * store * c,size_res => power_c); calc <= resize (arg => power_a - power_b + power_c + (store * d) - e,size_res => calc);pipeline_reg <= pipeline_reg(pipeline_reg'high -1 downto 0 ) & calc; op <= to_slv(pipeline_reg(pipeline_reg'high)(8 downto 0));end if;
end process;
end Behavioral;对于 109 Ω的电阻输入,温度应报告为 23.7°C。我们可以在下面的定点仿真中看到,结果符合预期,精度在可接受的范围内。

使用浮点包实现相同的功能,以类似的方式实现
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.FLOAT_pkg.ALL; -- Use the floating-point package
entity FloatingPointPolynomial isPort (clk : in STD_LOGIC;x : in float32; -- Input x as a 32-bit floating-point numbery : out float32 -- Output y as a 32-bit floating-point number );
end FloatingPointPolynomial;
architecture Behavioral of FloatingPointPolynomial is-- Define constants for the polynomial coefficientsconstant a4 : float32 := TO_float(2.00E-09);constant a3 : float32 := TO_float(-4.00E-07);constant a2 : float32 := TO_float(0.011);constant a1 : float32 := TO_float(2.403);constant a0 : float32 := TO_float(-251.26);signal x2, x3, x4 : float32; -- Intermediate powers of xsignal term4, term3, term2, term1 : float32; -- Polynomial termssignal res : float32;type reg_array is array (9 downto 0) of float32;signal pipeline_reg : reg_array;
beginprocess(clk)beginif rising_edge(clk) then-- Calculate powers of xx2 <= x * x;x3 <= x2 * x;x4 <= x3 * x;-- Calculate each term in the polynomialterm4 <= a4 * x4;term3 <= a3 * x3;term2 <= a2 * x2;term1 <= a1 * x;-- Calculate final resultres <= term4 + term3 + term2 + term1 + a0;pipeline_reg <= pipeline_reg(pipeline_reg'high -1 downto 0 ) & res;y <= (pipeline_reg(pipeline_reg'high));end if;end process;
end Behavioral;仿真再次显示了预期的结果,作为浮点结果,我们得到的结果也包括分数元素。

因此,定点和浮点都能够实现定义的算法。
为了了解利用所需的资源,决定将这两种算数实现都以 K26 SoM 为目标进行综合。
运行综合将识别每个模块所需的资源。
正如预期的那样,定点实现所需的逻辑占用空间比浮点实现所需的小得多。
 定点实现
定点实现  浮点实现
浮点实现 我们不仅需要考虑逻辑占用空间,还需要考虑时序性能。考虑到这一点,将两个设计都设置为 200 MHz 运行,并从一开始就实现了基准时序收敛。
实现时序收敛比定点收敛更重要,这在浮点实现中是可以预料到的。不得不重新审视设计,并在几个关键阶段实现流水线,因为最初的代码只是为了确定占用空间的差异。
值得注意的是,Versal 系列中的 DSP58 支持浮点运算,但它不能直接从 float32 映射到 DSP。为了利用此功能,我们需要实例化配置为 FP32 操作的 DSP58,或者利用 Vivado IP 集成器提供的浮点 IP。
总结这篇博客,正如预期的那样,在使用 VHDL 中的浮点库时,逻辑占用空间存在很大差异。
建议在必要时利用定点,并在绝对必要时限制浮点。
相关文章:

FPGA定点和浮点数学运算-实例对比
在创建 RTL 示例时,经常使用 VHDL 2008 附带的 VHDL 包。它提供了出色的功能,可以高效地处理定点数,当然,它们也是可综合的。该包的一些优点包括: 有符号和无符号(后缀和后缀)定点向量。轻松将定…...

MySQL Binlog 数据恢复全指南
MySQL Binlog 数据恢复全指南 一、Binlog 核心概念 1. 什么是 Binlog? Binlog(二进制日志)是 MySQL 记录所有修改数据的 SQL 语句的日志文件,采用二进制格式存储。它是 MySQL 最重要的日志之一,具有三大核心功能&am…...

python版若依框架开发:后端开发规范
python版若依框架开发 从0起步,扬帆起航。 python版若依部署代码生成指南,迅速落地CURD!项目结构解析前端开发规范后端开发规范文章目录 python版若依框架开发1.启动命令2.配置⽂件3.上传配置1.启动命令 本项⽬⾃定义了两个启动命令 pyhton app.py --env=devpython app.p…...

Linux编程:2、进程基础知识
一、进程基本概念 1、进程与程序的区别 程序:静态的可执行文件(如电脑中的vs2022安装程序)。进程:程序的动态执行过程(如启动后的vs2022实例),是操作系统分配资源的单位(如 CPU 时…...

时序数据库IoTDB与EdgeX Foundry集成适配服务介绍
一、背景介绍 EdgeX Foundry:由Linux基金会运维的开放源码边缘计算软件框架,自2017年开源后广泛应用于全球各行业场景。VMware自2018年起在中国社区推广EdgeX技术,拓展生态,并持续贡献代码。IoTDB:由Apache基…...

Android第十二次面试-多线程和字符串算法总结
多线程的创建与常见使用方法 一、多线程创建方式 1. 继承Thread类 class MyThread extends Thread {Overridepublic void run() {// 线程执行逻辑System.out.println(Thread.currentThread().getName() " is running");} }// 使用 MyThread thread new …...

ES6——数组扩展之Set数组
在ES6(ECMAScript 2015)中,JavaScript的Set对象提供了一种存储任何值唯一性的方式,类似于数组但又不需要索引访问。这对于需要确保元素唯一性的场景非常有用。Set对象本身并不直接提供数组那样的方法来操作数据(例如ma…...

Cursor Rules 使用
前言 最近在使用 Cursor 进行编程辅助时,发现 AI 生成的代码风格和当前的代码风格大相径庭。而且有时它会输出很奇怪的代码,总是不符合预期。 遂引出本篇,介绍一下 Rules ,它就可以做一些规范约束之类的事情。 什么是 Cursor R…...

服务器数据恢复—服务器raid5阵列崩溃如何恢复数据?
服务器数据恢复环境&故障: 某品牌型号为X3850服务器上有一组由14块数据盘和1块热备盘组建的raid5磁盘阵列。 服务器在正常使用过程中突然崩溃,管理员查看raid5阵列故障情况的时发现磁盘阵列中有2块硬盘掉线,但是热备盘没有启用。 服务器数…...

Go语言堆内存管理
Go堆内存管理 1. Go内存模型层级结构 Golang内存管理模型与TCMalloc的设计极其相似。基本轮廓和概念也几乎相同,只是一些规则和流程存在差异。 2. Go内存管理的基本概念 Go内存管理的许多概念在TCMalloc中已经有了,含义是相同的,只是名字有…...

【DAY41】简单CNN
内容来自浙大疏锦行python打卡训练营 浙大疏锦行 知识点: 数据增强卷积神经网络定义的写法batch归一化:调整一个批次的分布,常用与图像数据特征图:只有卷积操作输出的才叫特征图调度器:直接修改基础学习率 卷积操作常…...

Rust 学习笔记:使用自定义命令扩展 Cargo
Rust 学习笔记:使用自定义命令扩展 Cargo Rust 学习笔记:使用自定义命令扩展 Cargo Rust 学习笔记:使用自定义命令扩展 Cargo Cargo 支持通过 $PATH 中的 cargo-something 形式的二进制文件拓展子命令,而无需修改 Cargo 本身。 …...
)
LeetCode 08.06 面试题 汉诺塔 (Java)
经典递归解决汉诺塔问题:清晰的三步移动策略 问题描述 在汉诺塔问题中,有 3 根柱子和 N 个大小不同的盘子,盘子初始按升序堆叠在第一根柱子上(最小的在顶部)。目标是将所有盘子移动到第三根柱子上,并满足…...

使用MinIO搭建自己的分布式文件存储
目录 引言: 一.什么是 MinIO ? 二.MinIO 的安装与部署: 三.Spring Cloud 集成 MinIO: 1.前提准备: (1)安装依赖: (2)配置MinIO连接: &…...

单元测试与QTestLib框架使用
一.单元测试的意义 在软件开发中,单元测试是指对软件中最小可测试单元(通常是函数、类的方法)进行隔离的、可重复的验证。进行单元测试具有以下重要意义: 1.提升代码质量与可靠性: 早期错误检测: 在开发…...

java面试场景题:QPS 短链系统怎么设计
以下是对文章的润色版本: 这道场景设计题,初看似乎业务简单,实则覆盖的知识点极为丰富: 高并发与高性能分布式 ID 生成机制;Redis Bloom Filter——高并发、低内存损耗的过滤组件知识;分库、分表海量数据存…...

java面试场景提题:
以下是润色后的文章,结构更清晰,语言更流畅,同时保留了技术细节: 应对百倍QPS增长的系统设计策略 整体架构设计思路 面对突发性百倍QPS增长,系统设计需从硬件、架构、代码、数据四个维度协同优化: 硬件层…...

K7 系列各种PCIE IP核的对比
上面三个IP 有什么区别,什么时候用呢? 7 series Integrated Block for PCIE AXI Memory Mapped to PCI Express DMA subsystem for PCI Express 特点 这是 Kintex-7 内置的 硬核 PCIe 模块。部分事务层也集成在里面,使用标准的PCIE 基本没…...

natapp 内网穿透失败
连不上网络错误调试排查详解 - NATAPP-内网穿透 基于ngrok的国内高速内网映射工具 如何将DNS服务器修改为114.114.114.114_百度知道 连不上/错误信息等问题解决汇总 - NATAPP-内网穿透 基于ngrok的国内高速内网映射工具 nslookup auth.natapp.cnping auth.natapp.cn...
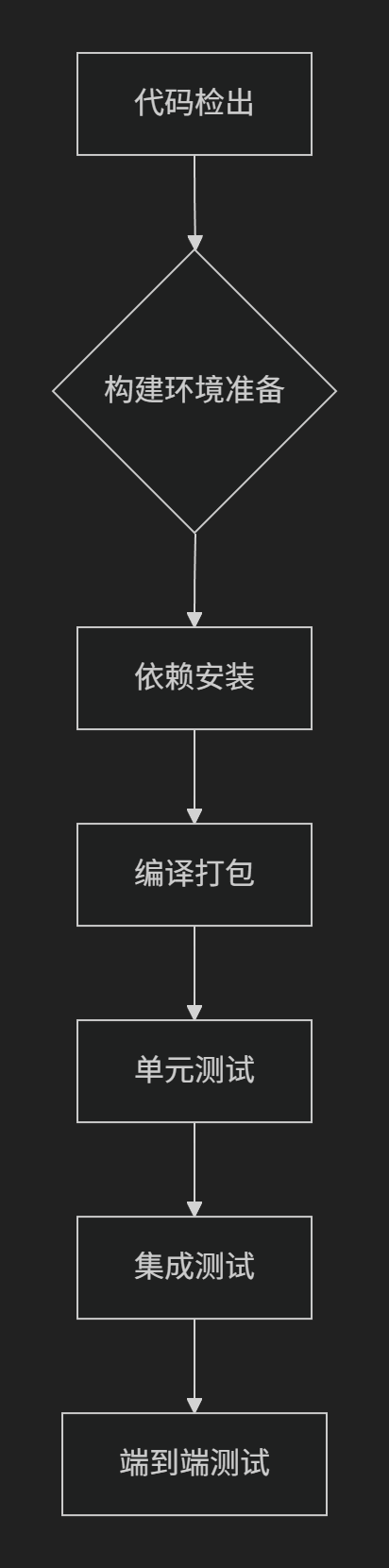
深入解析CI/CD开发流程
引言:主播最近实习的时候发现部门里面使用的是CI/CD这样的集成开发部署,但是自己不是太了解什么意思,所以就自己查了一下ci/cd相关的资料,整理分享了一下 一、CI/CD CI/CD是持续集成和持续交付部署的缩写,旨在简化并…...

Docke启动Ktransformers部署Qwen3MOE模型实战与性能测试
docker运行Ktransformers部署Qwen3MOE模型实战及 性能测试 最开始拉取ktransformers:v0.3.1-AVX512版本,发现无论如何都启动不了大模型,后来发现是cpu不支持avx512指令集。 由于本地cpu不支持amx指令集,因此下载avx2版本镜像: …...

应用分享 | 精准生成和时序控制!AWG在确定性三量子比特纠缠光子源中的应用
在量子技术飞速发展的今天,实现高效稳定的量子态操控是推动量子计算、量子通信等领域迈向实用化的关键。任意波形发生器(AWG)作为精准信号控制的核心设备,在量子实验中发挥着不可或缺的作用。丹麦哥本哈根大学的研究团队基于单个量…...

相机--相机标定实操
教程 camera_calibration移动画面示例 usb_cam使用介绍和下载 标定流程 单目相机标定 我使用的是USB相机,所以直接使用ros的usb_cam功能包驱动相机闭关获取实时图像,然后用ros的camera_calibration标定相机。 1,下载usb_cam和camera_calibration: …...

深入理解汇编语言中的顺序与分支结构
本文将结合Visual Studio环境配置、顺序结构编程和分支结构实现,全面解析汇编语言中的核心编程概念。通过实际案例演示无符号/有符号数处理、分段函数实现和逻辑表达式短路计算等关键技术。 一、汇编环境配置回顾(Win32MASM) 在Visual Studi…...

DAY43 复习日
浙大疏锦行-CSDN博客 kaggle找到一个图像数据集,用cnn网络进行训练并且用grad-cam做可视化 进阶:把项目拆分成多个文件 src/config.py: 用于存放项目配置,例如文件路径、学习率、批次大小等。 # src/config.py# Paths DATA_DIR "data…...

【仿生机器人】仿生机器人智能架构:从感知到个性的完整设计
仿生机器人智能架构:从感知到个性的完整设计 仿生机器人不仅需要模拟人类的外表,更需要具备类人的认知、情感和个性特征。本研究提出了一个综合性的软件架构,实现了从环境感知到情感生成、从实时交互到人格塑造的完整智能系统。该架构突破了…...

【业务框架】3C-相机-Cinemachine
概述 插件,做相机需求,等于相机老师傅多年经验总结的工具 Feature Transform:略Control Camera:控制相机参数Noise:增加随机性Blend:CameraBrain的混合列表指定一个虚拟相机到另一个相机的过渡ÿ…...

【Auto.js例程】华为备忘录导出到其他手机
目录 问题描述方法步骤1.安装下载Visual Studio Code2.安装扩展3.找到Auto.js插件,并安装插件4.启动服务器5.连接手机6.撰写脚本并运行7.本文实现功能的代码8.启动手机上的换机软件 问题描述 问题背景:华为手机换成一加手机,华为备忘录无法批…...

单片机的低功耗模式
什么是低功耗? STM32的低功耗(low power mode)特性是其嵌入式处理器系列的一个重要优势,特别适用于需要长时间运行且功耗敏感的应用场景,如便携式设备、物联网设备、智能家居系统等。 在很多应用场合中都对电子设备的…...

架构师级考验!飞算 JavaAI 炫技赛:AI 辅助编程解决老项目难题
当十年前 Hibernate 框架的 N1 查询隐患在深夜持续困扰排查,当 SpringMVC 控制器中错综复杂的业务逻辑在跨语言迁移时令人抓狂,企业数字化进程中的百万行老系统,已然成为暗藏危机的 “技术债冰山”。而此刻,飞算科技全新发布的 Ja…...
