函数与数列的交汇融合
前情概要
现行的新高考对数列的考查难度增加,那么整理与数列交汇融合的相关题目就显得非常必要了。
典例剖析
- 依托函数,利用导数,求数列的最值;
№ 1 、 \color{blue}{№ 1、} №1、 等差数列 { a n } \{a_{n}\} {an} 的前 n n n 项和为 S n S_{n} Sn, 已知 S 10 = 0 S_{10}=0 S10=0, S 15 = 25 S_{15}=25 S15=25, 则 n ⋅ S n n\cdot S_{n} n⋅Sn 的最小值为__________.
解: 由于数列 { a n } \{a_{n}\} {an} 为等差数列, 故可设 S n = a n 2 + b n S_{n}=an^{2}+bn Sn=an2+bn, 则 { 100 a + 10 b = 0 225 a + 15 b = 25 \left\{\begin{array}{l}{100a+10b=0}\\{225a+15b=25}\end{array}\right. {100a+10b=0225a+15b=25,
解得 a = 1 3 a=\cfrac{1}{3} a=31 , b = − 10 3 b=-\cfrac{10}{3} b=−310, 则 S n = 1 3 n 2 − 10 3 n S_{n}=\cfrac{1}{3}n^{2}-\cfrac{10}{3}n Sn=31n2−310n,
从而 n ⋅ S n = 1 3 n 3 − 10 3 n 2 n\cdot S_{n}=\cfrac{1}{3}n^{3}-\cfrac{10}{3}n^{2} n⋅Sn=31n3−310n2,其依托对应的函数为 y = 1 3 x 3 − 10 3 x 2 y=\cfrac{1}{3}x^{3}-\cfrac{10}{3}x^{2} y=31x3−310x2,
对函数 y = 1 3 x 3 − 10 3 x 2 y=\cfrac{1}{3}x^{3}-\cfrac{10}{3}x^{2} y=31x3−310x2,由于 n ∈ N ∗ n\in N^* n∈N∗,故不妨限定 x > 0 x>0 x>0,
先求函数的单调性, y ′ = x 2 − 20 3 x = x ( x − 20 3 ) y'=x^2-\cfrac{20}{3}x=x(x-\cfrac{20}{3}) y′=x2−320x=x(x−320),
当 x < 20 3 x<\cfrac{20}{3} x<320时, y ′ < 0 y'<0 y′<0,函数单调递减,当 x > 20 3 x>\cfrac{20}{3} x>320时, y ′ > 0 y'>0 y′>0,函数单调递增;
则当 x = 20 3 x=\cfrac{20}{3} x=320 时, y y y 取极小值,
则 n ⋅ S n = 1 3 n 3 − 10 3 n 2 n\cdot S_{n}=\cfrac{1}{3}n^{3}-\cfrac{10}{3}n^{2} n⋅Sn=31n3−310n2在 { 1 , 2 , 3 , 4 , 5 , 6 } \{1,2,3,4,5,6\} {1,2,3,4,5,6} 上单调递减,在 { 7 , 8 , 9 , ⋯ , } \{7,8,9,\cdots,\} {7,8,9,⋯,} 上单调递增,
又当 n = 6 n=6 n=6 时, 6 S 6 = − 48 6S_{6}=-48 6S6=−48,当 n = 7 n=7 n=7 时, 7 S 7 = − 49 7S_{7}=-49 7S7=−49,
故当 n = 7 n=7 n=7 时, n ⋅ S n n\cdot S_{n} n⋅Sn的最小值为 − 49 -49 −49.
- 依托函数,使用裂项相消法求数列的前 n n n项的和
№ 2 、 \color{blue}{№ 2、} №2、 设函数 f ( x ) = x m + a x f(x)=x^{m}+ax f(x)=xm+ax 的导数 f ′ ( x ) = 2 x + 2 f'(x)=2x+2 f′(x)=2x+2,求数列 { 1 f ( n ) } \{\cfrac{1}{f(n)}\} {f(n)1} ( n ∈ N ∗ ) (n\in N^{*}) (n∈N∗) 的前 n n n 项和 S n S_{n} Sn
解 因为 f ′ ( x ) = 2 x + 2 f'(x)=2x+2 f′(x)=2x+2, 所以 f ( x ) = x 2 + 2 x + C f(x)=x^{2}+2x+C f(x)=x2+2x+C,
因为 f ( x ) = x m + a x f(x)=x^{m}+ax f(x)=xm+ax, 所以 m = 2 m=2 m=2, a = 2 a=2 a=2, C = 0 C=0 C=0,
即 f ( x ) = x 2 + 2 x f(x)=x^{2}+2x f(x)=x2+2x,所以 f ( n ) = n 2 + 2 n = n ( n + 2 ) f(n)=n^{2}+2n=n(n+2) f(n)=n2+2n=n(n+2),
从而设 b n = 1 f ( n ) = 1 2 ( 1 n − 1 n + 2 ) b_{n}=\cfrac{1}{f(n)}=\cfrac{1}{2}(\cfrac{1}{n}-\cfrac{1}{n+2}) bn=f(n)1=21(n1−n+21),
所以 S n = b 1 + b 2 + b 3 + ⋯ + b n − 1 + b n S_{n}=b_{1}+b_{2}+b_{3}+\cdots+b_{n-1}+b_{n} Sn=b1+b2+b3+⋯+bn−1+bn
= 1 2 [ ( 1 − 1 3 ) + ( 1 2 − 1 4 ) + ⋯ + ( 1 n − 1 − 1 n + 1 ) + ( 1 n − 1 n + 2 ) ] =\cfrac{1}{2}\left[(1-\cfrac{1}{3})+(\cfrac{1}{2}-\cfrac{1}{4})+\cdots+(\cfrac{1}{n-1}-\cfrac{1}{n+1})+(\cfrac{1}{n}-\cfrac{1}{n+2})\right] =21[(1−3
相关文章:

函数与数列的交汇融合
前情概要 现行的新高考对数列的考查难度增加,那么整理与数列交汇融合的相关题目就显得非常必要了。 典例剖析 依托函数,利用导数,求数列的最值;№ 1 、 \color{blue}{№ 1、} №1、 等差数列 { a n } \{a_{n}\} {an} 的前 n n n 项和为 S n S_{n} Sn, 已知 S 10…...

怎么让自己ip显示外省?一文说清操作
在互联网时代,IP地址不仅关联网络连接,还可能影响IP属地显示。那么,手机和电脑用户怎么让自己IP显示外省?一文说清操作要点。 二、4种主流方法详解 要让自己的IP显示为外省地址,主要有以下几种方法: …...

【Docker】容器安全之非root用户运行
【Docker】容器安全之非root用户运行 1. 场景2. 原 Dockerfile 内容3. 整改结果4. 非 root 用户带来的潜在问题4.1 文件夹读写权限异常4.2 验证文件夹权限 1. 场景 最近有个项目要交付,第三方测试对项目源码扫描后发现一个问题,服务的 Dockerfile 都未指…...

汽车车载软件平台化项目规模颗粒度选择的一些探讨
汽车进入 SDV 时代后,车载软件研发呈现出开源生态构建、电子架构升级、基础软件标准化、本土供应链崛起、AI 原生架构普及、云边协同开发等趋势,这些趋势促使车载软件研发面临新挑战,如何构建适应这些变化的平台化架构成为车企与 Tier 1 的战…...

【八股消消乐】构建微服务架构体系—服务注册与发现
😊你好,我是小航,一个正在变秃、变强的文艺倾年。 🔔本专栏《八股消消乐》旨在记录个人所背的八股文,包括Java/Go开发、Vue开发、系统架构、大模型开发、具身智能、机器学习、深度学习、力扣算法等相关知识点ÿ…...

大数据+智能零售:数字化变革下的“智慧新零售”密码
大数据+智能零售:数字化变革下的“智慧新零售”密码 大家好,今天咱们聊聊一个火到不行的话题:大数据在智能零售中的应用。这个领域,不仅是技术的“硬核战场”,更是商业创新的风口浪尖。谁能玩转数据,谁就能掌控消费者心智,实现销售爆发。 咱们不搞枯燥学术,而是用最“…...

C++_核心编程_菱形继承
4.6.8 菱形继承 菱形继承概念: 两个派生类继承同一个基类 又有某个类同时继承者两个派生类 这种继承被称为菱形继承,或者钻石继承 菱形继承问题: 1. 羊继承了动物的数据, 驼同样继承了动物的数据࿰…...

掌握Git核心:版本控制、分支管理与远程操作
前言 无论热爱技术的阅读者你是希望掌握Git的企业级应用,能够深刻理解Git操作过程及操作原理,理解工作区暂存区、版本库的含义;还是想要掌握Git的版本、分支管理,自由的进行版本回退、撤销、修改等Git操作方式与背后原理和通过分…...

c#,Powershell,mmsys.cpl,使用Win32 API展示音频设备属性对话框
常识(基础) 众所周知,mmsys.cpl使管理音频设备的控制面板小工具, 其能产生一个对话框(属性表)让我们查看和修改各设备的详细属性: 在音量合成器中单击音频输出设备的小图标也能实现这个效果&a…...

STM标准库-TIM旋转编码器
文章目录 一、编码器接口1.1简介1.2正交编码器1.3编码器接口基本结构**1. 模块与 STM32 配置的映射关系****2. 设计实现步骤(核心流程)****① 硬件规划****② 时钟使能****③ GPIO 配置(对应架构图 “GPIO” 模块)****④ 时基单元…...

深入解析JVM工作原理:从字节码到机器指令的全过程
一、JVM概述 Java虚拟机(JVM)是Java平台的核心组件,它实现了Java"一次编写,到处运行"的理念。JVM是一个抽象的计算机器,它有自己的指令集和运行时内存管理机制。 JVM的主要职责: 加载:读取.class文件并验…...

MCP通信方式之Streamable HTTP
目录 一、前言二、三种传输方式对比1、Stdio和 HTTP SSE工作原理2、Streamable HTTP3、Streamable HTTP解决什么问题三、Streamable HTTP MCP设计原理四、Streamable HTTP MCP demo演示1、MCP server示例2、MCP Client示例一、前言 2025年5月9日,MCP(Model Context Protocol)…...

第七十三篇 从电影院售票到停车场计数:生活场景解析Java原子类精髓
目录 一、原子类基础:电影院售票系统1.1 传统售票的并发问题1.2 原子类解决方案 二、原子类家族:超市收银系统2.1 基础类型原子类2.2 数组类型原子类 三、CAS机制深度解析:停车场管理系统3.1 CAS工作原理3.2 车位计数器实现 四、高性能实践&a…...

【原创】基于视觉模型+FFmpeg+MoviePy实现短视频自动化二次编辑+多赛道
AI视频处理系统功能总览 🎯 系统概述 这是一个智能短视频自动化处理系统,专门用于视频搬运和二次创作。系统支持多赛道配置,可以根据不同的内容类型(如"外国人少系列"等)应用不同的处理策略。 Ἵ…...

C++----剖析list
前面学习了vector和string,接下来剖析stl中的list,在数据库中学习过,list逻辑上是连续的,但是存储中是分散的,这是与vector这种数组类型不同的地方。所以list中的元素设置为一个结构体,将list设计成双向的&…...

纳米AI搜索与百度AI搜、豆包的核心差异解析
一、技术定位与设计目标 1、纳米AI搜索:轻量化边缘计算导向 专注于实时数据处理与资源受限环境下的高效响应,通过算法优化和模型压缩技术,实现在物联网设备、智能终端等低功耗场景的本地化部署。其核心优势在于减少云端依赖,保障…...

不到 2 个月,OpenAI 火速用 Rust 重写 AI 编程工具。尤雨溪也觉得 Rust 香!
一、OpenAI 用 Rust 重写 Codex CLI OpenAI 已用 Rust 语言重写了其 AI 命令行编程工具 Codex CLI,理由是此举能提升性能和安全性,同时避免对 Node.js 的依赖。他们认为 Node.js “可能让部分用户感到沮丧或成为使用障碍”。 Codex 是一款实验性编程代理…...

人工智能:网络安全的“智能守护者”
在数字化时代,网络安全已经成为企业和个人面临的重大挑战。随着网络攻击的复杂性和频率不断增加,传统的安全防护手段已经难以应对。人工智能(AI)技术的出现为网络安全带来了新的希望和解决方案。本文将探讨人工智能在网络安全中的…...

Python60日基础学习打卡Day46
一、 什么是注意力 注意力机制的由来本质是从onehot-elmo-selfattention-encoder-bert这就是一条不断提取特征的路。各有各的特点,也可以说由弱到强。 其中注意力机制是一种让模型学会「选择性关注重要信息」的特征提取器,就像人类视觉会自动忽略背景&…...

综述论文解读:Editing Large Language Models: Problems, Methods, and Opportunities
论文为大语言模型知识编辑综述,发表于自然语言处理顶会ACL(原文链接)。由于目前存在广泛的模型编辑技术,但一个统一全面的分析评估方法,所以本文: 1、对LLM的编辑方法进行了详尽、公平的实证分析,探讨了它们各自的优势…...

WEB3全栈开发——面试专业技能点P1Node.js / Web3.js / Ethers.js
一、Node.js 事件循环 Node.js 的事件循环(Event Loop)是其异步编程的核心机制,它使得 Node.js 可以在单线程中实现非阻塞 I/O 操作。 🔁 简要原理 Node.js 是基于 libuv 实现的,它使用事件循环来处理非阻塞操作。事件…...

Vscode下Go语言环境配置
前言 本文介绍了vscode下Go语言开发环境的快速配置,为新手小白快速上手Go语言提供帮助。 1.下载官方Vscode 这步比较基础,已经安装好的同学可以直接快进到第二步 官方安装包地址:https://code.visualstudio.com/ 双击一直点击下一步即可,记…...

Java八股文——MySQL篇
文章目录 Java八股文——MySQL篇慢查询如何定位慢查询?如何分析慢SQLExplain标准答案 索引索引类型索引底层数据结构什么是聚簇索引什么是非聚簇索引?(二级索引)(回表)聚集索引选取规则回表查询 什么是覆盖…...

Oracle数据库学习笔记 - 创建、备份和恢复
Oracle数据库学习笔记 创建,备份和恢复 Oracle 版本基于11g 尽量不使用图形界面方式,操作适用于linux和windows 创建数据库 创建实例 # 步骤1:设置环境变量 export ORACLE_SIDmyorcl export ORACLE_HOME/u01/app/oracle/product/19.0.0/dbh…...

Go语言--语法基础5--基本数据类型--输入输出(1)
I : input 输入操作 格式化输入 scanf O : output 输出操作 格式化输出 printf 标准输入 》键盘设备 》 Stdin 标准输出 》显示器终端 》 Stdout 异常输出 》显示器终端 》 Stderr 1 、输入语句 Go 语言的标准输出流在打印到屏幕时有些参数跟别的语言…...

永磁同步电机无速度算法--自适应龙贝格观测器
一、原理介绍 传统龙伯格观测器,在设计观测器反馈增益矩阵K时,为简化分析与设计,根据静止两相坐标系下的对称关系,只引入了K、K,两个常系数,且在实际应用时,大多是通过试凑找到一组合适的反馈增益系数缺乏…...
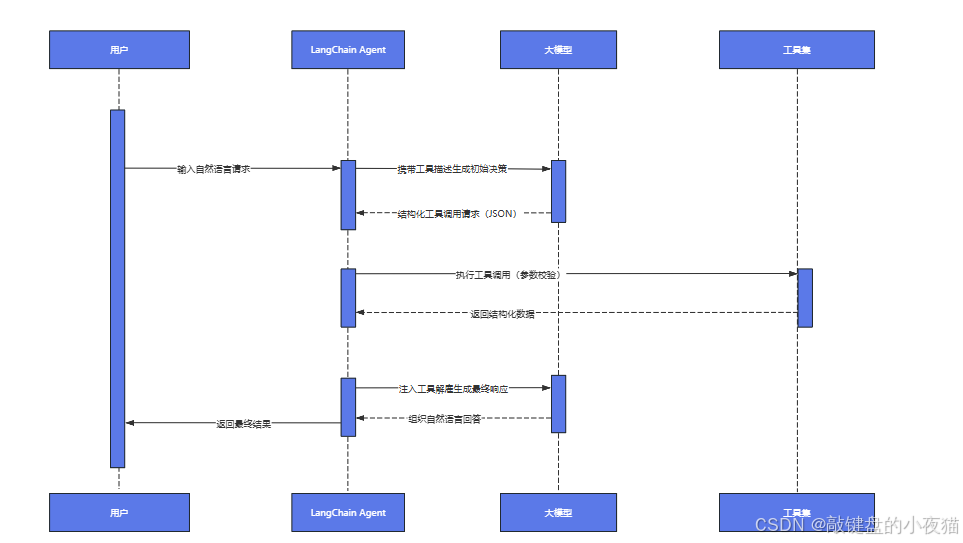
LangChain工具集成实战:构建智能问答系统完整指南
导读:在人工智能快速发展的今天,如何构建一个既能理解自然语言又能调用外部工具的智能问答系统,成为许多开发者面临的核心挑战。本文将为您提供一套完整的解决方案,从LangChain内置工具包的基础架构到复杂系统的工程实践。 文章深…...

【razor】x264 在 的intra-refresh和IDR插帧
你提到的是这样一个情况: 使用 DirectShow 采集,帧率稳定(如回调了20帧)使用 x264 的 total intra refresh 模式(intra-refresh=1) 进行编码但编码过程中「隔几十秒才有一帧intra(关键帧)」这不正常,具体分析如下: 🎯 一、问题核心 x264 的 intra refresh 模式(特…...

分库分表的取舍
文章目录 大数据量下采用**水平分表**的缺点**1. 跨表查询复杂性与性能下降****2. 数据分布不均衡****3. 分布式事务与一致性问题****4. 扩展性受限****5. 查询条件限制与索引管理复杂****6. 数据迁移与维护成本高****7. 业务逻辑复杂度增加****总结** shardingJdbc分片策略**1…...

随机算法一文深度全解
随机算法一文深度全解 一、随机算法基础1.1 定义与核心特性1.2 算法优势与局限 二、随机算法经典案例2.1 随机化快速排序原理推导问题分析与策略代码实现(Python、Java、C) 2.2 蒙特卡罗方法计算 π 值原理推导问题分析与策略代码实现(Python…...
