力扣HOT100之二分查找:4. 寻找两个正序数组的中位数

这道题如果没有时间复杂度的限制的话,相当好做,但是这道题要求时间复杂度为O(log(m + n)),思路很难想,我看了一圈题解,发现华南溜达虎的视频讲得还不错,我是参考他的思路写出来的,这里把他的思路记录一下。
对于两个升序排列的数组,我们只需要在两个数组中分别找到下标i和j,使得nums1[i]左侧的元素与nums2[j]左侧的元素个数之和最多比nums1[i]与nums2[j]及其右边的元素数量多1,则我们就找到了中位数,下面简单举个例子。
 对于上面两个数组,我们通过寻找合适的下标
对于上面两个数组,我们通过寻找合适的下标i和j,使得左侧的元素个数为5。
对于上面的数组,元素个数为10,所以剩下的元素也为5个,针对这种情况,我们只需要选出红色圈内的最大值(max(nums1[i - 1], nums2[j - 1])),再选出右侧元素中的最小值(min(nums1[i], nums2[j])),再求平均值即可求出中位数。
对于下面的数组,元素个数为9,所以剩下的元素个数为4个,针对这种情况,我们只需要选出红色圈内的最大值,即可求出中位数。
那么,我们如何选出合适的i和j呢?我这里就直接引用作者的约束了。
1. nums1[i - 1] < nums1[i]
2. nums2[j - 1] < nums2[j]
3. nums1[i - 1] < nums2[j]
4. nums2[j - 1] < nums1[i]
第一条和第二条约束是为了保证两个数组都是递增的,在本题显然成立,因此不用开率;第三条和第四条则确保了nums1[i]和nums2[j]左侧的所有元素恰好为合并数组中的前一半元素。在满足以上性质以后,我们可以进行进一步分析,左侧的元素可以用一根线串起来,如下所示。

用绳子将左侧的所有元素穿起来,绳子两头的右边一位就是对应的元素下标i和j,同时我们不难发现,无论元素总数为奇数还是偶数,绳子上的元素个数均等于i + j,因此我们一旦确定了i,j也随之确定了。我们要做的就是在nums1中找到i,然后就能找到中位数。我们在初始化时,默认将i设置为nums1的中间位置,然后j通过绳子的长度-i得到。上面的第三条和第四条性质并不总是同时满足,但是一定不会同时不满足,这是两个数组均为递增数组的性质决定的。当第三条性质不满足时,则说明上面的线太长,而下面的线太短,此时我们需要将上面的线头向左移,当第四条性质不满足时,说明下面的线太长,而上面的线太短,此时我们需要将上面的线头向右移。当同时满足以上四条性质时,则找到了合适的位置。以上说的是最常见的情况,也就是绳子的两端可以落在两个数组中间的情况,下面我们来看一下绳子落在数组边界之外的情况:
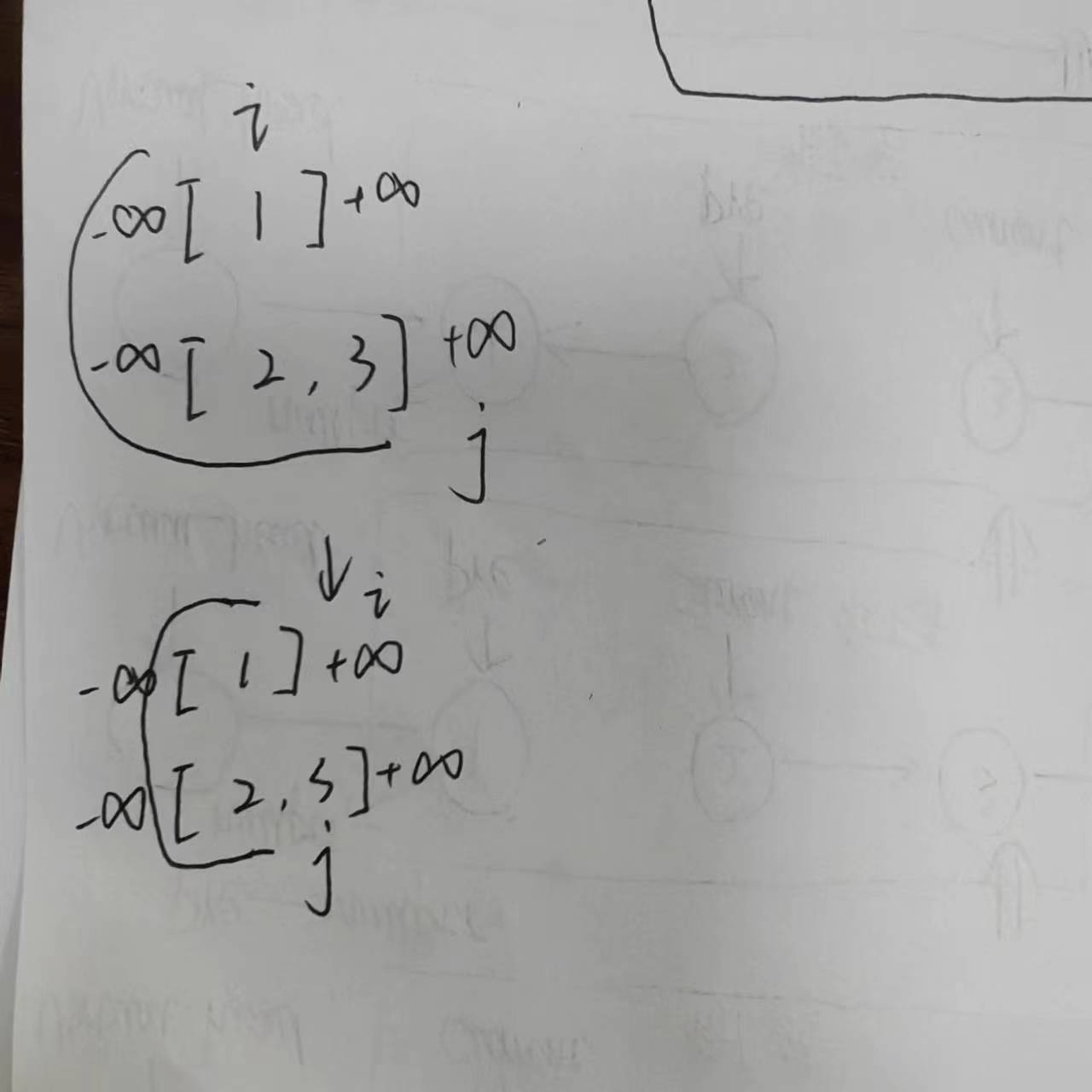
当我们进行初始化时,i = (0 + nums1.size()) / 2,为0,此时j的初始位置发生了越界。当我们找到合适的i和j后,我们发现此时i发生了越界,此时线上的元素为[1, 2],我们返回其中的较大值作为中位数。但是我们是怎么从初始状态转移到最终的状态的呢?在初始状态下,i的左边没有元素,在判断条件三的时候显然会发生越界访问,此时我们观察到条件四也不满足,为了维护上述性质的成立,3和4只能由一条不成立,条件四不成立是板上钉钉的事实,我们需要执行条件四的维护操作,而条件三应当想办法使其成立,在这种情况下,应当假设i左边存在一个元素(仅在发生左边越界的时候才会出现),无论nums[j]为何值,都有nums1[i - 1] < nums2[j]成立,所以应当假设数组的左侧有INT_MIN,当发生左侧越界时,则用INT_MIN来代替nums[i - 1],当nums2发生左侧越界时也是同理。当发生右侧越界时,我们采用INT_MAX来代替越界的值。
感觉这道题目还是很晦涩难懂,真的好难想╮(╯▽╰)╭
class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {if(nums1.size() > nums2.size())swap(nums1, nums2); //确保nums1总是较短的那个数组int m = nums1.size();int n = nums2.size();int left = 0, right = m; //在nums1中进行二分查找while(left <= right){int i = (left + right) / 2;int j = (m + n + 1) / 2 - i; //绳子的长度为(m + n + 1) / 2int left1 = (i == 0) ? INT_MIN : nums1[i - 1];int right1 = (i == m) ? INT_MAX : nums1[i];int left2 = (j == 0) ? INT_MIN : nums2[j - 1];int right2 = (j == n) ? INT_MAX : nums2[j];if(left1 <= right2 && left2 <= right1){if((m + n) % 2 == 1)return max(left1, left2);return (min(right1, right2) + max(left1, left2)) / 2.0;}else if(left1 > right2)right = i - 1;else left = i + 1;}return 0;}
};
相关文章:
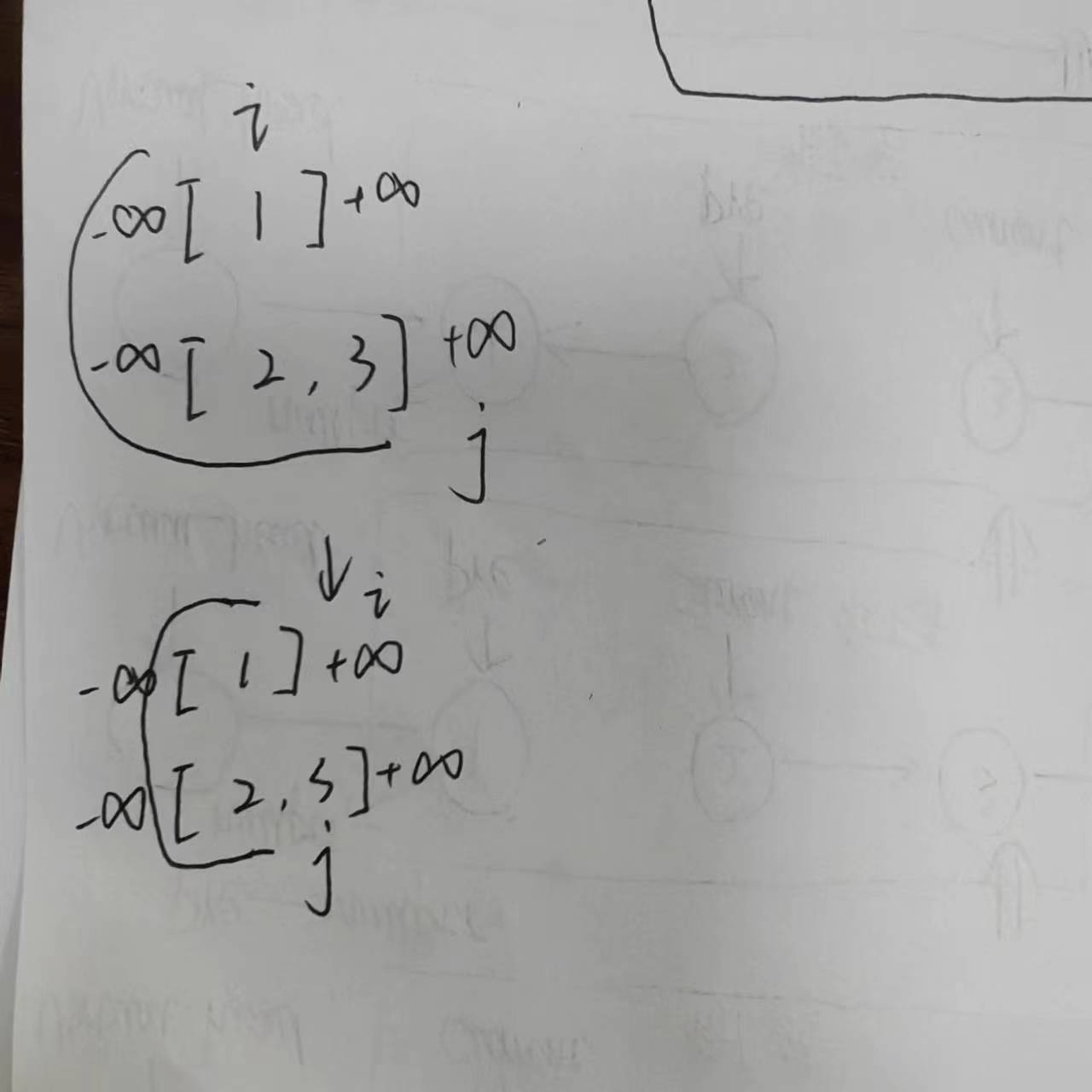
力扣HOT100之二分查找:4. 寻找两个正序数组的中位数
这道题如果没有时间复杂度的限制的话,相当好做,但是这道题要求时间复杂度为O(log(m n)),思路很难想,我看了一圈题解,发现华南溜达虎的视频讲得还不错,我是参考他的思路写出来的,这里把他的思路…...

PyTorch——损失函数与反向传播(8)
Loss Functions 越小越好 L1loss MSELoss 损失函数 CrossEntyopyLoss 损失函数 import torch from torch.nn import L1Loss from torch import nn# 创建输入和目标张量,用于后续的损失计算 inputs torch.tensor([1,2,3],dtypetorch.float32) targets torch.tenso…...

macOS 升级 bash 到最新版本
macOS 的默认「终端」,千年不变的版本。 》〉bash --version GNU bash, version 3.2.57(1)-release (arm64-apple-darwin24) Copyright (C) 2007 Free Software Foundation, Inc. 官方 bash.git - bash 已经将 bash 升级到了 5.2的大版本。 macOS 最新版系统的 ba…...

Linux下如何查看一个端口被什么进程占用? 该进程又打开了哪些文件?
Linux下如何查看一个端口被什么进程占用? 该进程又打开了哪些文件? 查看端口 1.使用lsof命令查看端口占用的进程 lsof可以列出系统上打开的文件,其中包括网络连接、进程信息等。 lsof -i:<端口号> 例如,如果需…...

力扣面试150题--课程表
Day 63 题目描述 做法 初次思路:本质就是将所有前置课程和后置课程作为一个有向图(前者指向后者),判断这个图是否是一个有向无环图(即是否存在拓扑排序)(本质做法是dfs) 做法&…...

用通俗的话解释下MCP是个啥?
在AI领域,模型的开发、部署和迭代速度日益加快,但随之而来的挑战也愈发显著:如何高效管理不同版本的模型?如何在复杂环境中确保模型的可追溯性和可复用性?如何实现跨团队、跨平台的模型协作? 在计算机领域…...

LeetCode 高频 SQL 50 题(基础版)之 【子查询】· 上
题目:1978. 上级经理已离职的公司员工 题解: select employee_id from Employees where salary<30000 and manager_id is not null and manager_id not in (select distinct employee_id from Employees ) order by employee_id题目:626.…...

Spark流水线+Gravitino+Marquez数据血缘采集
1.Openlinage和Marquez简介 1.1 OpenLineage 概述 OpenLineage 是一个开放标准和框架,用于跨工具、平台和系统捕获数据血缘信息。它定义了通用的数据血缘模型和API,允许不同的数据处理工具(如ETL、调度器、数据仓库)以标准化格…...
、TimesNet和LSTM三种模型,并提供可视化展示)
一个完整的时间序列异常检测系统,使用Flask作为后端框架,实现了AE(自编码器)、TimesNet和LSTM三种模型,并提供可视化展示
时间序列异常检测系统 下面是一个完整的时间序列异常检测系统,使用Flask作为后端框架,实现了AE(自编码器)、TimesNet和LSTM三种模型,并提供可视化展示。 系统概述 这个系统能够: 从多种来源加载时间序列数据使用三种先进算法进行异常检测可视化展示原始数据、重建数据和…...

深度学习在非线性场景中的核心应用领域及向量/张量数据处理案例,结合工业、金融等领域的实际落地场景分析
一、工业场景:非线性缺陷检测与预测 1. 半导体晶圆缺陷检测 问题:微米级划痕、颗粒污染等缺陷形态复杂,与正常纹理呈非线性关系。解决方案: 输入张量:高分辨率晶圆图像 → 三维张量 (Batch, Height,…...

基于微信小程序的车位共享平台的设计与实现源码数据库文档
摘 要 近年来,随着国民经济的飞速发展,城镇化进程的步伐加快,城市人口急剧增长,人们的生活水平持续改善,特别是大中型城市,城市的交通规模日益增大,汽车的保有量不断提高,然而城市的…...

多模态大语言模型arxiv论文略读(111)
SEA: Supervised Embedding Alignment for Token-Level Visual-Textual Integration in MLLMs ➡️ 论文标题:SEA: Supervised Embedding Alignment for Token-Level Visual-Textual Integration in MLLMs ➡️ 论文作者:Yuanyang Yin, Yaqi Zhao, Yaji…...

网页端 VUE+C#/FastAPI获取客户端IP和hostname
1 IP可以获取,但是发现获取到的是服务端的IP,如何解决呢。 如果采用nginx反向代理,那么可以在conf/nginx.conf文件中配置 location /WebApi/ { proxy_pass http://localhost:5000/; #这个/会替换location种的WebApi路径 #关键,加…...

一个自动反汇编脚本
一、环境 wsl ubuntu18.04、python3.6 二、目的 调试程序,需要分析第三方库。希望能将多个库自动转为汇编文件。 三、使用方法 将该脚本下载,进入wsl,进入到该脚本所有文件夹。 请使用 python 脚本名.py 运行。 1)、运行…...

函数与数列的交汇融合
前情概要 现行的新高考对数列的考查难度增加,那么整理与数列交汇融合的相关题目就显得非常必要了。 典例剖析 依托函数,利用导数,求数列的最值;№ 1 、 \color{blue}{№ 1、} №1、 等差数列 { a n } \{a_{n}\} {an} 的前 n n n 项和为 S n S_{n} Sn, 已知 S 10…...

怎么让自己ip显示外省?一文说清操作
在互联网时代,IP地址不仅关联网络连接,还可能影响IP属地显示。那么,手机和电脑用户怎么让自己IP显示外省?一文说清操作要点。 二、4种主流方法详解 要让自己的IP显示为外省地址,主要有以下几种方法: …...

【Docker】容器安全之非root用户运行
【Docker】容器安全之非root用户运行 1. 场景2. 原 Dockerfile 内容3. 整改结果4. 非 root 用户带来的潜在问题4.1 文件夹读写权限异常4.2 验证文件夹权限 1. 场景 最近有个项目要交付,第三方测试对项目源码扫描后发现一个问题,服务的 Dockerfile 都未指…...

汽车车载软件平台化项目规模颗粒度选择的一些探讨
汽车进入 SDV 时代后,车载软件研发呈现出开源生态构建、电子架构升级、基础软件标准化、本土供应链崛起、AI 原生架构普及、云边协同开发等趋势,这些趋势促使车载软件研发面临新挑战,如何构建适应这些变化的平台化架构成为车企与 Tier 1 的战…...

【八股消消乐】构建微服务架构体系—服务注册与发现
😊你好,我是小航,一个正在变秃、变强的文艺倾年。 🔔本专栏《八股消消乐》旨在记录个人所背的八股文,包括Java/Go开发、Vue开发、系统架构、大模型开发、具身智能、机器学习、深度学习、力扣算法等相关知识点ÿ…...

大数据+智能零售:数字化变革下的“智慧新零售”密码
大数据+智能零售:数字化变革下的“智慧新零售”密码 大家好,今天咱们聊聊一个火到不行的话题:大数据在智能零售中的应用。这个领域,不仅是技术的“硬核战场”,更是商业创新的风口浪尖。谁能玩转数据,谁就能掌控消费者心智,实现销售爆发。 咱们不搞枯燥学术,而是用最“…...

C++_核心编程_菱形继承
4.6.8 菱形继承 菱形继承概念: 两个派生类继承同一个基类 又有某个类同时继承者两个派生类 这种继承被称为菱形继承,或者钻石继承 菱形继承问题: 1. 羊继承了动物的数据, 驼同样继承了动物的数据࿰…...

掌握Git核心:版本控制、分支管理与远程操作
前言 无论热爱技术的阅读者你是希望掌握Git的企业级应用,能够深刻理解Git操作过程及操作原理,理解工作区暂存区、版本库的含义;还是想要掌握Git的版本、分支管理,自由的进行版本回退、撤销、修改等Git操作方式与背后原理和通过分…...

c#,Powershell,mmsys.cpl,使用Win32 API展示音频设备属性对话框
常识(基础) 众所周知,mmsys.cpl使管理音频设备的控制面板小工具, 其能产生一个对话框(属性表)让我们查看和修改各设备的详细属性: 在音量合成器中单击音频输出设备的小图标也能实现这个效果&a…...

STM标准库-TIM旋转编码器
文章目录 一、编码器接口1.1简介1.2正交编码器1.3编码器接口基本结构**1. 模块与 STM32 配置的映射关系****2. 设计实现步骤(核心流程)****① 硬件规划****② 时钟使能****③ GPIO 配置(对应架构图 “GPIO” 模块)****④ 时基单元…...

深入解析JVM工作原理:从字节码到机器指令的全过程
一、JVM概述 Java虚拟机(JVM)是Java平台的核心组件,它实现了Java"一次编写,到处运行"的理念。JVM是一个抽象的计算机器,它有自己的指令集和运行时内存管理机制。 JVM的主要职责: 加载:读取.class文件并验…...

MCP通信方式之Streamable HTTP
目录 一、前言二、三种传输方式对比1、Stdio和 HTTP SSE工作原理2、Streamable HTTP3、Streamable HTTP解决什么问题三、Streamable HTTP MCP设计原理四、Streamable HTTP MCP demo演示1、MCP server示例2、MCP Client示例一、前言 2025年5月9日,MCP(Model Context Protocol)…...

第七十三篇 从电影院售票到停车场计数:生活场景解析Java原子类精髓
目录 一、原子类基础:电影院售票系统1.1 传统售票的并发问题1.2 原子类解决方案 二、原子类家族:超市收银系统2.1 基础类型原子类2.2 数组类型原子类 三、CAS机制深度解析:停车场管理系统3.1 CAS工作原理3.2 车位计数器实现 四、高性能实践&a…...

【原创】基于视觉模型+FFmpeg+MoviePy实现短视频自动化二次编辑+多赛道
AI视频处理系统功能总览 🎯 系统概述 这是一个智能短视频自动化处理系统,专门用于视频搬运和二次创作。系统支持多赛道配置,可以根据不同的内容类型(如"外国人少系列"等)应用不同的处理策略。 Ἵ…...

C++----剖析list
前面学习了vector和string,接下来剖析stl中的list,在数据库中学习过,list逻辑上是连续的,但是存储中是分散的,这是与vector这种数组类型不同的地方。所以list中的元素设置为一个结构体,将list设计成双向的&…...

纳米AI搜索与百度AI搜、豆包的核心差异解析
一、技术定位与设计目标 1、纳米AI搜索:轻量化边缘计算导向 专注于实时数据处理与资源受限环境下的高效响应,通过算法优化和模型压缩技术,实现在物联网设备、智能终端等低功耗场景的本地化部署。其核心优势在于减少云端依赖,保障…...
