c# 完成恩尼格玛加密扩展
c# 完成恩尼格玛加密扩展
- 恩尼格玛
- 扩展为可见字符
- 恩尼格玛的设备
- 原始字符顺序
- 转子的设置
- 反射器的设置
- 连接板的设置
- 初始数据的设置
- 第一版 C# 代码
- 第二版 C# 代码
- 总结
恩尼格玛
在之前,我们使用 python 实现了一版恩尼格玛的加密算法,但是这一版,转子的字符仅仅只支持26个字母,且无大小写的区分,所以适用范围就相当有限了。
具体的恩尼格玛的说明,可以参考文章:https://blog.csdn.net/weixin_30807779/article/details/98515455
具体来说,恩尼格玛实现了加密和解密使用的是同一套算法,关键就在于有一个反射器,在使用相同转子的情况下,按照相同的顺序输入加密前和加密后的字符就可以得到互换后的字符,且一一对应。
CSDN 文盲老顾的博客,https://blog.csdn.net/superwfei
老顾的个人社区,https://bbs.csdn.net/forums/bfba6c5031e64c13aa7c60eebe858a5f?category=10003&typeId=3364713
扩展为可见字符
为了使恩尼格玛的算法适用范围更广,我们需要将所有的可见 ASCII 码都加入到编码之中。
恩尼格玛的设备
原始字符顺序
这个字符顺序,算是一个基本设置,毕竟 ASCII 从 32 到 127 的顺序还是有点不太习惯,当然,按照这个顺序也没有问题,也可以自己定义字符顺序
// abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789`~!@#$%^&*()-_=+[{]}\|;:'",./<>?
转子的设置
对于恩尼格玛的转子来说,其实就是原始字符串中,第一个字符对应打乱后转子字符里的第一个字符,第二个字符对应第二个字符。
如果是多个转子,需要注意,不是第一个转子的第一个字符对应第二个转子的字符,而是原始字符的第一个字符,对应第二个转子的第一个字符哦。
反射器的设置
反射器,是一个比较特殊的路径,它是将所有字符两两对应的关系,这个反射器,我们也可以用字符串来进行描述,比如第一个字符对应最后一个字符,如果是双数数量的字符就没什么毛病,如果是单数数量的字符,那么中间的字符对应它自身即可。
连接板的设置
同理,连接板和反射板差不多,这里使用的是和反射器一样的设置,即字符两两对应,如果想增加复杂度,也可以和转子一样,不按照两两对应的方式,这个之后我们再讨论
初始数据的设置
那么,对于恩尼格玛的算法来说,我们需要一个初始字符串,然后一个反射板,一个连接板,至少一个转子这样的数据。
那么,我们就只需要一个原始字符串,然后将原始字符串随机打乱至少3次,每次打乱的数据作为原始数据存放到一个数组中。
这个数组至少是四个元素,第一个元素,就是原始字符串,第二个元素作为连接板的数据,第三个元素作为反射器的设置,第四个及之后的所有元素,作为转子的数据即可。
第一版 C# 代码
那么我们的第一版代码就可以根据之前我们的 py 代码进行构建了
public static string Enigma(string keyword, string[] EnigmaRotors){string result = string.Empty;int l = EnigmaRotors.Length;int cl = EnigmaRotors[1].Length;if (l < 4){return keyword;}Hashtable link = new Hashtable();Hashtable reverser = new Hashtable();for (int i = 0; i < cl; i++){link[EnigmaRotors[1].Substring(i, 1)] = EnigmaRotors[1].Substring(cl - i - 1, 1);}for (int i = 0; i < cl; i++){reverser[EnigmaRotors[2].Substring(i, 1)] = EnigmaRotors[2].Substring(cl - i - 1, 1);}for (int i = 0; i < keyword.Length; i++){List<string> lst = new List<string>();for (int j = 0; j < EnigmaRotors.Length - 3; j++){lst.Add(EnigmaRotors[3 + j]);int t = (int)Math.Floor(i / Math.Pow(cl, j)) % cl;if (t > 0){// 正转lst[lst.Count - 1] = lst[lst.Count - 1].Substring(t) + lst[lst.Count - 1].Substring(0, t);// 反转//lst[lst.Count - 1] = lst[lst.Count - 1].Substring(cl - t) + lst[lst.Count - 1].Substring(0, cl - t);}}string r = keyword.Substring(i, 1);r = link[r].ToString();for (int j = 0; j < lst.Count; j++){string rotor = lst[j];r = rotor.Substring(EnigmaRotors[0].IndexOf(r), 1);}r = reverser[r].ToString();for (int j = 0; j < lst.Count; j++){string rotor = lst[lst.Count - j - 1];r = EnigmaRotors[0].Substring(rotor.IndexOf(r), 1);}r = link[r].ToString();result += r;}return result;}在代码中,我们对于原始数据 EnigmaRotors 的长度进行了验证,当该数据至少有四个元素的时候,才进行加密算法。当然,我这里没有对每个元素的字符是否一致进行验证,其实基本上也不太需要。
其中,在方法中,link 就是连接板,reverser 就是反射器,我们使用 Hashtable 来代替字典。
int t = (int)Math.Floor(i / Math.Pow(cl, j)) % cl;
这一行来计算当前输入字符的顺序,是否需要对每个转子进行转动。
string r = keyword.Substring(i, 1);
而循环中,这行代码之前,为转子确定状态
之后,则是按照连接板,转子,反射器,转子,连接板的顺序,对字符进行替换的过程了。
不过,这一版需要传输一个非常大的 string[] 对象作为参数,实在是有点不太友好。
第二版 C# 代码
public static string Enigma(string keyword, string chars,int seed,int len = 1)
在这一版,我们可以不再输入一个长字符串数组当做参数了
我们只需要将原始字符串作为参数
然后给出一个随机函数的种子,用来限定每次使用随机函数打乱字符串的时候,可以得出相同的结果
最后,给出一个转子的数量,最低是1
这个版本,与上一版的区别就在于,EnigmaRotors 的数据,是由随机种子,原始字符串和转子数量来自动生成的。
即,我们使用一个 List 来存放临时数据,最后将该数据的 ToArray() 结果保存为 EnigmaRotors 即可。
Random rnd = new Random(seed);
List<string> lst = new List<string>();
// 原始字符串
lst.Add(chars);
// 连接版
lst.Add(Shuffle(rnd,chars));
// 反射器
lst.Add(Shuffle(rnd,chars));
for (int i=0;i<len;i++){// 增加转子lst.Add(Shuffle(rnd,chars));
}
EnigmaRotors = lst.ToArray();
以上代码,插入到第一版的代码中函数定义的开始部分即可。后续代码与第一版并无区别。
然后,我们还需要实现一个洗牌的函数 Shuffle,具体该怎么打乱字符串,自己简单实现一下即可
public string Shuffle(Random rnd,string chars){List<byte> result = new List<byte>();List<byte> lst = new List<byte>();lst.AddRange(Encoding.UTF8.GetBytes(chars));while (lst.Count > 0){int n = rnd.Next(lst.Count);result.Add(lst[n]);lst.RemoveAt(n);}return Encoding.UTF8.GetString(result);
}
总结
由于 c# 没有 python 那么多的语法糖,所以很多内容,需要自己靠循环一点点来实现,也因为 c# 没有那么多第三方包,类似洗牌,打乱字符串这种方法,也得自己来实现。
但其实这些内容都是基本内容,自己实现起来,也没有那么复杂。
总的来说,用 c# 来实现恩尼格玛加密,也是一件比较简单的事情。
相关文章:

c# 完成恩尼格玛加密扩展
c# 完成恩尼格玛加密扩展 恩尼格玛扩展为可见字符恩尼格玛的设备原始字符顺序转子的设置反射器的设置连接板的设置 初始数据的设置第一版 C# 代码第二版 C# 代码 总结 恩尼格玛 在之前,我们使用 python 实现了一版恩尼格玛的加密算法,但是这一版&#x…...

华为 “一底双长焦” 专利公布,引领移动影像新变革
6 月 6 日,国家知识产权局公布的一项专利发明申请吸引了众多目光,该专利发明人为华为技术有限公司,名为 “光学镜头、摄像头模组及电子设备” 。从展示的技术图来看,这一光学镜头呈现出独特的 “一底双镜头结构”,其中…...

老年生活照护实训室建设规划:照护质量评估与持续改进实训体系
随着人口老龄化程度的不断加深,老年生活照护需求日益增长,对专业照护人才的培养提出了更高要求。老年生活照护实训室建设方案作为培养高素质照护人才的重要载体,其核心在于构建科学完善的照护质量评估与持续改进实训体系。通过该体系的建设&a…...

【python深度学习】Day 48 PyTorch基本数据类型与操作
知识点: 随机张量的生成:torch.randn函数卷积和池化的计算公式(可以不掌握,模型会自动计算的)pytorch的广播机制:加法和乘法的广播机制 ps:numpy运算也有类似的广播机制,基本一致 作…...

Go深入学习延迟语句
1 延迟语句是什么 编程的时候,经常会需要申请一些资源,比如数据库连接、文件、锁等,这些资源需要再使用后释放掉,否则会造成内存泄露。但是编程人员经常容易忘记释放这些资源,从而造成一些事故。 Go 语言直接在语言层…...

【大模型】【推荐系统】LLM在推荐系统中的应用价值
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点B.4 两大推荐方法 C 模型结构C.1 知识蒸馏(训练过程)C.2 轻量推理(部署过程) D 实验设计E 个人总结 A 论文出处 论文题目:SLMRec:Distilling…...

uni-app学习笔记二十九--数据缓存
uni.setStorageSync(KEY,DATA) 将 data 存储在本地缓存中指定的 key 中,如果有多个key相同,下面的会覆盖掉原上面的该 key 对应的内容,这是一个同步接口。数据可以是字符串,可以是数组。 <script setup>uni.setStorageSyn…...

csharp基础....
int[][] jaggedArray new int[3][]; jaggedArray[0] new int[] { 1, 2 }; jaggedArray[1] new int[] { 3, 4, 5 }; jaggedArray[2] new int[] { 6, 7, 8, 9 }; 嵌套 反转和排序 List<int> list new List<int> { 1, 2, 3, 4, 5 }; list.Reverse(); Cons…...

【C/C++】EBO空基类优化介绍
空对象优化(Empty Base Optimization,简称 EBO)是 C 编译器的一种 优化技术,用于消除空类作为基类时占用的内存空间,从而避免浪费空间、提升结构体或类的存储效率。 1 什么是“空对象”? 一个**空类&#…...

工作邮箱收到钓鱼邮件,点了链接进去无法访问,会有什么问题吗?
没事的,很可能是被安全网关拦截了。最近做勒索实验,有感而发,不要乱点击邮箱中的附件。 最初我们采用钓鱼邮件投递恶意载荷,发现邮件网关把我们的 exe/bat 程序直接拦截了,换成压缩包也一样拦截了,载荷始终…...

基于安卓的线上考试APP源码数据库文档
摘 要 21世纪的今天,随着社会的不断发展与进步,人们对于信息科学化的认识,已由低层次向高层次发展,由原来的感性认识向理性认识提高,管理工作的重要性已逐渐被人们所认识,科学化的管理,使信息存…...

【数据结构】顺序表和链表详解(下)
前言:上期我们从顺序表开始讲到了单链表的概念,分类,和实现,而这期我们来将相较于单链表没那么常用的双向链表。 文章目录 一、双向链表二,双向链表的实现一,增1,头插2,尾插3&#x…...

【系统架构设计师】绪论-系统架构概述
目录 绪论 系统架构概述 单选题 绪论 系统架构概述 单选题 1、软件方法学是以软件开发方法为研究对象的学科。其中,()是先对最高居次中的问题进行定义、设计、编程和测试,而将其中未解决的问题作为一个子任务放到下一层次中去…...

SQL-事务(2025.6.6-2025.6.7学习篇)
1、简介 事务是一组操作的集合,它是一个不可分割的工作单位,事务会把所有的操作作为一个整体一起向系统提交或撤销操作请求,即这些操作要么同时成功,要么同时失败。 默认MySQL的事务是自动提交的,也就是说࿰…...

OpenCV 图像通道的分离与合并
一、知识点 1、一张彩色图像可以由R、G、B三个通道的灰度图合并而成。 2、void split(InputArray m, OutputArrayOfArrays mv); (1)、将多通道阵列划分为几个单通道阵列。 (2)、参数说明: m: 要分离的多通道阵列。 mv: 输出的vector容器,每个元素都…...
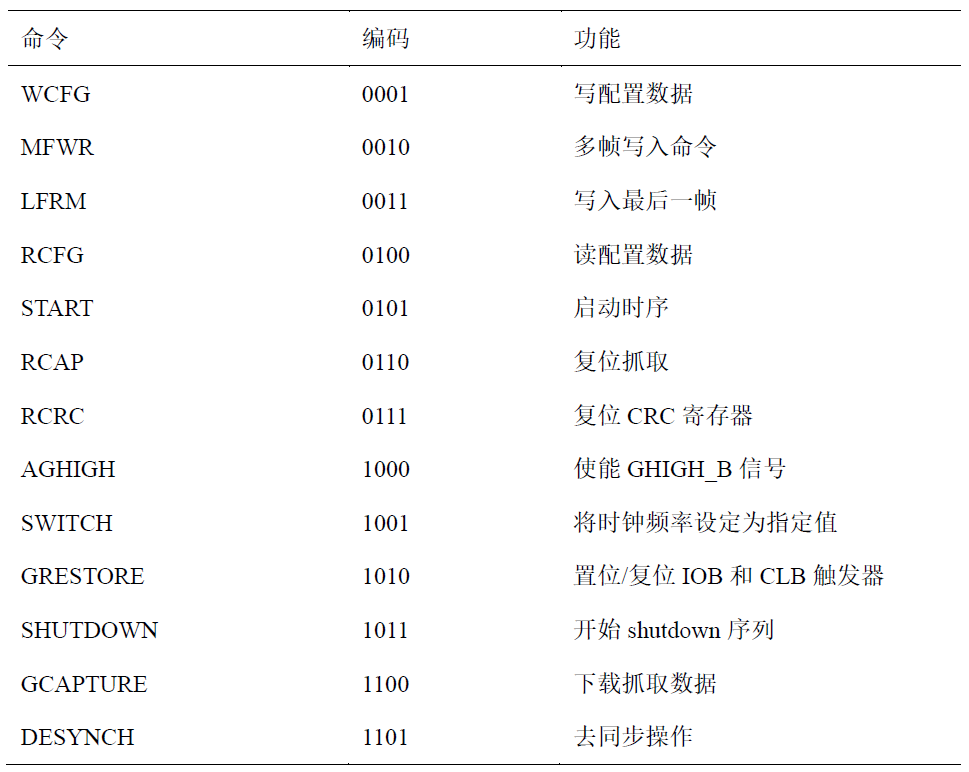
Virtex II 系列FPGA的配置原理
对FPGA 芯片的配置,本质上是将根据设计生成的包含配置命令和配置数据的比特流文件写入到配置存储器中。 1 配置模式 Virtex II 系列FPGA 一共有五种配置模式,配置模式的选择是根据管脚M[2:0]来决定。 (1)串行配置模式 串行配置模…...

蓝桥杯 国赛2024python(b组)题目(1-3)
第一题 试卷答题页 - 蓝桥云课 问题描述 在今年蓝桥杯的决赛中,一共有 1010 道题目,每道题目的分数依次为 55 分,55 分,1010 分,1010 分,1515 分,1515 分,2020 分,2020 分…...

低代码平台前端页面表格字段绑定与后端数据传输交互主要有哪些方式?华为云Astro在这方面有哪些方式?
目录 🔧 一、低代码平台中常见的数据绑定与交互方式 1. 接口绑定(API 调用) 2. 数据源绑定(DataSource) 3. 变量中转(临时变量 / 页面状态) 4. 数据模型绑定(模型驱动) 🌐 二、华为云 Astro 轻应用的实现方式 ✅ 1. 数据源绑定(API服务+API网关) ✅ 2. 变…...

stm32——UART和USART
串口通信协议UART和USART 1. UART与USART协议详解 特性UART (Universal Asynchronous Receiver/Transmitter)USART (Universal Synchronous Asynchronous Receiver/Transmitter)全称通用异步收发器通用同步/异步收发器同步/异步异步:不共享时钟,数据通过…...

算法题(165):汉诺塔问题
审题: 本题需要我们找到最优的汉诺塔搬法然后将移动路径输出 思路: 方法一:递归 我们先分析题目 n为2的情况,我们先将第一个盘子移动到三号柱子上,然后再将二号盘子移动到二号柱子上 n为3的情况,我们先将前…...

玄机——某次行业攻防应急响应(带镜像)
今天给大家带来一次攻防实战演练复现的过程。 文章目录 简介靶机简介1.根据流量包分析首个进行扫描攻击的IP是2.根据流量包分析第二个扫描攻击的IP和漏扫工具,以flag{x.x.x.x&工具名}3.提交频繁爆破密钥的IP及爆破次数,以flag{ip&次数}提交4. 提…...

低代码逻辑引擎配置化实战:三步穿透审批记录查询
在堆积如山的报销单中埋头寻找某笔特殊费用的审批轨迹在跨部门协作时被追问"这个合同到底卡在哪个环节" 在快节奏的办公自动化场景中,这些场景是很常见的,传统OA系统中分散的审批记录查询方式往往太繁琐。 为破解这一痛点,在JVS低…...

深入理解React Hooks的原理与实践
深入理解React Hooks的原理与实践 引言 React Hooks 自 2018 年 React 16.8 发布以来,彻底改变了前端开发者的编码方式。它通过函数式组件提供了状态管理和生命周期等功能,取代了传统的类组件,使得代码更加简洁、复用性更强。然而ÿ…...

WEB3技术重要吗,还是可有可无?
我从几个角度给你一个全面、理性、技术导向的回答: ✅ 一、Web3 技术的重要性:“有意义,但不是万能” Web3 技术并不是可有可无的噱头,而是一种在特定场景下提供独特价值的技术体系。 它重要的原因包括: 1. 重构数字…...

Python 隐藏法宝:双下划线 _ _Dunder_ _
你可能不知道,Python里那些用双下划线包裹的"魔法方法"(Dunder方法),其实是提升代码质量的绝佳工具。但有趣的是,很多经验丰富的开发者对这些方法也只是一知半解。 先说句公道话: 这其实情有可原。因为在多数情况下&am…...

《视觉SLAM十四讲》自用笔记 第三讲:三维空间刚体运动
第三讲 三维空间刚体运动 3.0 目标 1.理解三维空间的刚体运动描述方式:旋转矩阵、变换矩阵、四元数和欧拉角。 2.掌握 Eigen 库的矩阵、几何模块使用方法。 3.1 旋转矩阵 3.1.1 点和向量,坐标系 三维空间中,刚体的运动可以用两个概念来…...

【Zephyr 系列 15】构建企业级 BLE 模块通用框架:驱动 + 事件 + 状态机 + 低功耗全栈设计
🧠关键词:Zephyr、BLE 模块、架构设计、驱动封装、事件机制、状态机、低功耗、可维护框架 📌面向读者:希望将 BLE 项目从“Demo 工程”升级为“企业可复用框架”的研发人员与技术负责人 📊预计字数:5500+ 字 🧭 前言:从 Demo 到产品化,架构该如何升级? 多数 BLE…...

Docker构建Vite项目内存溢出:从Heap Limit报错到完美解决的剖析
问题现象:诡异的"消失的index.html" 最近在CI/CD流水线中遇到诡异现象:使用Docker构建Vite项目时,dist目录中缺少关键的index.html文件,但本地构建完全正常。报错截图显示关键信息: FATAL ERROR: Reached heap limit Allocation failed - JavaScript heap out…...
)
Linux运维新人自用笔记(乌班图apt命令和dpkg命令、两系统指令区别,rpm解决路径依赖、免安装配置java环境)
内容全为个人理解和自查资料梳理,欢迎各位大神指点! 每天学习较为零散。 day17 一、Ubuntu apt命令和dpkg命令 二进制命令配置文件数据文件,打包好的单个文件 Windows :.exe macos:.dmg 后缀适用系统安装方式.d…...

vm+ubuntu24.04扩展磁盘
vmubuntu24.04扩展磁盘 $ lsblk $ sudo fdisk -l 1.修复 GPT 表警告 $ sudo parted /dev/sda print当询问是否修复时,输入 Fix2.扩展物理分区 /dev/sda3 $ sudo growpart /dev/sda 33.刷新物理卷 (PV) $ sudo pvresize /dev/sda3检查可用的扩展空间. $ sudo vgd…...
