数学建模期末速成 主成分分析的基本步骤
设有 n n n个研究对象, m m m个指标变量 x 1 , x 2 , ⋯ , x m x_1,x_2,\cdots,x_m x1,x2,⋯,xm,第 i i i个对象关于第 j j j个指标取值为 a i j a_{ij} aij,构造数据矩阵 A = ( a i j ) n × m A=\left(\begin{array}{c}a_{ij}\end{array}\right)_{n\times m} A=(aij)n×m
(1)对原来的 m m m个指标进行标准化,得到标准化的指标变量
y j = x j − μ j s j , j = 1 , 2 , ⋯ , m , 式中 : μ j = 1 n ∑ i = 1 n a i j ; s i = 1 n − 1 ∑ i = 1 n ( a i j − μ j ) 2 y_{j}=\frac{x_{j}-\mu_{j}}{s_{j}},\quad j=1,2,\cdots,m\:,\\\text{式中}:\mu_{j}=\frac{1}{n}\sum_{i=1}^{n}a_{ij};s_{i}\:=\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}\left(a_{ij}-\mu_{j}\right)^{2}} yj=sjxj−μj,j=1,2,⋯,m,式中:μj=n1i=1∑naij;si=n−11i=1∑n(aij−μj)2
对应地,得到标准化的数据矩阵
B = ( b i j ) n × m , 其中 b i j = a i j − μ j s j , i = 1 , 2 , ⋯ , n , j = 1 , 2 , ⋯ , m B=(b_{ij})_{n\times m},\text{其中 }b_{ij}=\frac{a_{ij}-\mu_{j}}{s_{j}},i=1,2,\cdots,n,j=1\:,\\2,\cdots,m B=(bij)n×m,其中 bij=sjaij−μj,i=1,2,⋯,n,j=1,2,⋯,m
(2)根据标准化的数据矩阵 B B B求出相关系数矩阵 R = ( r i j ) m × n R=(r_{ij})_{m\times n} R=(rij)m×n其中
b i j = a i j − μ j s j , i = 1 , 2 , ⋯ , n , j = 1 , 2 , ⋯ , m b_{ij}=\frac{a_{ij}-\mu_{j}}{s_{j}},i=1\:,2\:,\cdots,n\:,j=1\:,2\:,\cdots,m bij=sjaij−μj,i=1,2,⋯,n,j=1,2,⋯,m
(3) 计算相关系数矩阵 R R R 的特征值 λ 1 ≥ λ 2 ≥ ⋯ ≥ λ m \lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_m λ1≥λ2≥⋯≥λm,及对应的标准正交化特征向量 u 1 , u 2 , ⋯ , u m u_1, u_2, \cdots, u_m u1,u2,⋯,um,其中 u j = [ u 1 j , u 2 j , ⋯ , u m j ] T u_j = [u_{1j}, u_{2j}, \cdots, u_{mj}]^T uj=[u1j,u2j,⋯,umj]T,由特征向量组成 p p p 个新的指标变量
{ F 1 = u 11 y 1 + u 21 y 2 + ⋯ + u m 1 y m , F 2 = u 12 y 1 + u 22 y 2 + ⋯ + u m 2 y m , ⋮ F m = u 1 m y 1 + u 2 m y 2 + ⋯ + u m m y m , \begin{cases} F_1 = u_{11} y_1 + u_{21} y_2 + \cdots + u_{m1} y_m, \\ F_2 = u_{12} y_1 + u_{22} y_2 + \cdots + u_{m2} y_m, \\ \vdots \\ F_m = u_{1m} y_1 + u_{2m} y_2 + \cdots + u_{mm} y_m, \end{cases} ⎩ ⎨ ⎧F1=u11y1+u21y2+⋯+um1ym,F2=u12y1+u22y2+⋯+um2ym,⋮Fm=u1my1+u2my2+⋯+ummym,
式中: F 1 F_1 F1 为第 1 主成分; F 2 F_2 F2 为第 2 主成分; ⋯ \cdots ⋯, F m F_m Fm 为第 m m m 主成分。
(4) 计算主成分贡献率及累积贡献率,主成分 F j F_j Fj 的贡献率为
w j = λ j ∑ k = 1 m λ k , j = 1 , 2 , ⋯ , m , w_j = \frac{\lambda_j}{\sum_{k=1}^m \lambda_k}, \quad j = 1, 2, \cdots, m, wj=∑k=1mλkλj,j=1,2,⋯,m,
前 i i i 个主成分的累积贡献率为
∑ k = 1 i λ k ∑ k = 1 m λ k \frac{\sum_{k=1}^i \lambda_k}{\sum_{k=1}^m \lambda_k} ∑k=1mλk∑k=1iλk
一般取累积贡献率达 85%以上的特征值 λ 1 , λ 2 , ⋯ , λ k \lambda_1, \lambda_2, \cdots, \lambda_k λ1,λ2,⋯,λk 所对应的第 1, 第 2, ⋯ \cdots ⋯,第 k ( k ≤ p ) k (k \leq p) k(k≤p) 主成分
(5) 最后利用得到的主成分 F 1 , F 2 , ⋯ , F k F_1, F_2, \cdots, F_k F1,F2,⋯,Fk 分析问题,或者继续进行评价、回归、聚类等其他建模
[!warning] 注意
主成分分析的结果受量纲的影响,由于各变量的单位可能不同,结果可能不同这是主成分分析的最大问题。因此,在实际问题中,需要先对各变量进行无量纲化处理,然后用协方差矩阵或相关系数矩阵进行分析。
补充
无量纲化处理
在数学建模中,无量纲化处理(Non-dimensionalization)是通过引入特征尺度将包含单位的物理量转化为无量纲量的过程。其核心目的是简化模型、减少参数数量、揭示变量间的本质关系,并提高数值计算的稳定性。
如何做到无量纲化?
-
选择特征尺度
针对每个变量(如时间、长度、速度等),选择一个具有物理意义的参考值(如初始值、平衡状态值、特征长度等)。例如:- 时间尺度:若系统周期为 ( T ),可将时间 ( t ) 转化为 ( \tilde{t} = t/T )。
- 长度尺度:若物体长度为 ( L ),可将坐标 ( x ) 转化为 ( \tilde{x} = x/L )。
-
变量替换
将原变量替换为无量纲形式,例如: v ~ = v v c ( v c 为特征速度) \tilde{v} = \frac{v}{v_c} \quad \text{(\( v_c \) 为特征速度)} v~=vcv(vc 为特征速度)3. 方程转化
将原方程中的变量和参数全部替换为无量纲量,整理后得到无量纲方程。
无量纲化的意义 -
简化模型结构
-
揭示尺度规律
-
数值计算稳定性
-
普适性分析
标准化
由于样本数据矩阵由多个指标组成,不同指标一般有不同的量纲,为消除量纲的影响,通常需要进行数据变换处理。常用的数据变换方法有:
- 中心化处理:先求出每个变量的样本平均值,再从原始数据中减去该变量的均值
b i j = a i j − μ j , i = 1 , ⋯ , n ; j = 1 , ⋯ , p , 式中 : μ j = ∑ i = 1 n a i j n b_{ij}=a_{ij}-\mu_{j}\:, \quad i=1\:,\cdots,n\:;j=1\:,\cdots,p\:,\\\text{式中}:\mu_j=\frac{\sum_{i=1}^na_{ij}}n bij=aij−μj,i=1,⋯,n;j=1,⋯,p,式中:μj=n∑i=1naij - 规格化处理:每一个变量的原始数据减去该变量中的最小值,再除以极差
b i j = a i j − min 1 ≤ i ≤ n ( a i j ) max 1 ≤ i ≤ n ( a i j ) − min 1 ≤ i ≤ n ( a i j ) , i = 1 , ⋯ , n ; j = 1 , ⋯ , p . b_{ij}=\frac{a_{ij}-\min_{1\leq i\leq n}\left(\:a_{ij}\:\right)}{\max_{1\leq i\leq n}\left(\:a_{ij}\:\right)-\min_{1\leq i\leq n}\left(\:a_{ij}\right)},\quad i=1\:,\cdots,n\:;j=1\:,\cdots,p. bij=max1≤i≤n(aij)−min1≤i≤n(aij)aij−min1≤i≤n(aij),i=1,⋯,n;j=1,⋯,p. - 标准化变换:先对每个变量进行中心化变换,然后用该变量的标准差进行标准化
b i j = a i j − μ j s j , i = 1 , ⋯ , n ; j = 1 , ⋯ , p , 式中 : μ j = ∑ i = 1 n a i j n ; s j = 1 n − 1 ∑ i = 1 n ( a i j − μ j ) 2 b_{ij}=\frac{a_{ij}-\mu_{j}}{s_{j}},\quad i=1\:,\cdots,n\:;j=1\:,\cdots,p\:,\\\text{式中}:\mu_{j}=\frac{\sum_{i=1}^{n}a_{ij}}{n};s_{j}=\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}\left(a_{ij}-\mu_{j}\right)^{2}} bij=sjaij−μj,i=1,⋯,n;j=1,⋯,p,式中:μj=n∑i=1naij;sj=n−11i=1∑n(aij−μj)2
相关文章:

数学建模期末速成 主成分分析的基本步骤
设有 n n n个研究对象, m m m个指标变量 x 1 , x 2 , ⋯ , x m x_1,x_2,\cdots,x_m x1,x2,⋯,xm,第 i i i个对象关于第 j j j个指标取值为 a i j a_{ij} aij,构造数据矩阵 A ( a i j ) n m A\left(\begin{array}{c}a_{ij}\end{array}\right)_{…...

视频音频去掉开头结尾 视频去掉前n秒后n秒 电视剧去掉开头歌曲
视频音频去掉开头结尾 视频去掉前n秒后n秒 视频音频去掉开头结尾 视频去掉前n秒后n秒 电视剧去掉开头歌曲 如果你有一些视频或者音频,你想去掉开头或结尾的几秒钟,那么你可以尝试一下这个工具,首先,我们来看一下,我们以…...

【在线五子棋对战】二、websocket 服务器搭建
文章目录 Ⅰ. WebSocket1、简介2、特点3、原理解析4、报文格式 Ⅱ. WebSocketpp1、认识2、常用接口3、websocketpp库搭建服务器搭建流程主体框架填充回调函数细节 4、编写 makefile 文件5、websocket客户端 Ⅰ. WebSocket 1、简介 WebSocket 是从 HTML5 开始支持的一种网页端…...

C++课设:从零开始打造影院订票系统
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、项目背景与需求分析二、系统架构设计…...

【计算机网络】数据链路层-滑动窗口协议
数据链路层滑动窗口协议 1. 三种协议对比表 特性停止-等待协议GBN协议SR协议窗口大小发送 1,接收 1发送 W (1<W≤2ⁿ-1),接收 1发送 C,接收 R确认方式单个确认累积确认选择性确认重传策略超时重传回退N帧重传选择性重传接收缓冲区…...

在linux系统上,如何安装Elasticsearch?
1.问题描述 当尝试连接时报错,报错内容为: elastic_transport.ConnectionError: Connection error caused by: ConnectionError(Connection error caused by: NewConnectionError(<urllib3.connection.HTTPConnection object at 0x7fd808b179d0>:…...
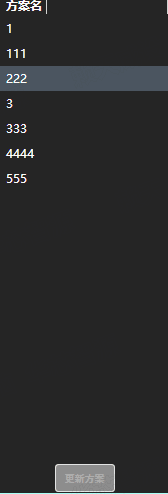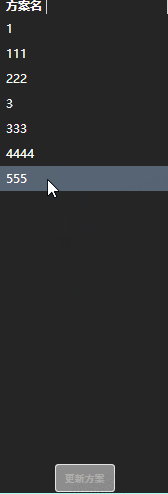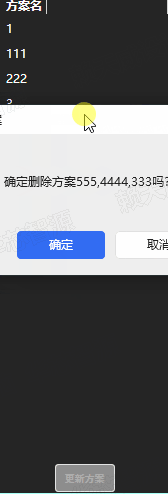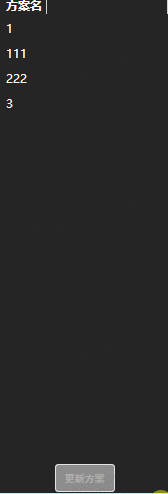
wpf Behaviors库实现支持多选操作进行后台绑定数据的ListView
<ListView ItemsSource"{Binding SchemeItems}" SelectionMode"Extended" VerticalAlignment"Stretch" HorizontalAlignment"Stretch"><ListView.ContextMenu><ContextMenu><MenuItem Header"删除" …...

【HarmonyOS 5】拍摄美化开发实践介绍以及详细案例
以下是 HarmonyOS 5 拍摄美化功能的简洁介绍,整合核心能力与技术亮点: 一、AI 影像创新 AI 魔法移图 系统级图像分层技术实现人物/物体自由拖拽、缩放与复制,突破传统构图限制。自动分离主体与背景,一键生成错位创意照&…...

《Vuejs设计与实现》第 8 章(挂载与更新)
目录 8.1 挂载子节点与属性 8.2 HTML Attributes 与 DOM Properties 8.3 设置元素属性的正确方式 8.4 处理 class 属性 8.5 卸载操作 8.6 区分 vnode 类型 8.7 事件处理优化 8.8 事件冒泡与更新时机问题 8.9 子节点的更新 8.10 文本节点和注释节点 8.11 片段…...

Ubuntu20.04中 Redis 的安装和配置
Ubuntu20.04 中 Redis 的安装和配置 Ubuntu 安装 MySQL 及其配置 1. Redis 的安装 更新系统包列表并安装 Redis : # 更新包管理工具 sudo apt update# -y:自动确认所有提示(非交互式安装) sudo apt install -y redis-server测…...

从游戏到自动驾驶:互联网时代强化学习如何让机器学会自主决策?
一、为什么机器需要“试错学习”?——强化学习的核心秘密 你有没有玩过《超级马里奥》?当你操控马里奥躲避乌龟、跳过悬崖时,其实就在用一种“试错”的方法学习最优路径。强化学习(Reinforcement Learning, RL)就是让…...

实验四:图像灰度处理
实验四 图像处理实验报告 目录 实验目的实验内容 原理描述Verilog HDL设计源代码Testbench仿真代码及仿真结果XDC文件配置下板测试 实验体会实验照片 实验目的 在实验三的基础上,将图片显示在显示器上,并进行灰度处理。 实验内容 原理描述 1. 图片的…...

asp.net mvc如何简化控制器逻辑
在ASP.NET MVC中,可以通过以下方法简化控制器逻辑: ASP.NET——MVC编程_aspnet mvc-CSDN博客 .NET/ASP.NET MVC Controller 控制器(IController控制器的创建过程) https://cloud.tencent.com/developer/article/1015115 【转载…...

解析“与此站点的连接不安全”警告:成因与应对策略
一、技术本质:SSL/TLS协议的信任链断裂 现代浏览器通过SSL/TLS协议建立加密通信,其核心在于证书颁发机构(CA)构建的信任链。当用户访问网站时,浏览器会验证服务器证书的有效性,包括: 证书链完…...

PyCharm和VS Code哪个更适合初学者
对于 Python 初学者来说,选择 VS Code 还是 PyCharm 取决于你的具体需求和使用场景。以下是两者的详细对比和推荐建议: VS Code 优点: 轻量级:启动速度快,占用资源少,适合在低端设备上运行。高度可定制&am…...

⚡️ Linux Docker 基本命令参数详解
🐳 Linux Docker 基本命令参数详解 📘 1. Docker 简介 Docker 是一个开源的容器化平台,它通过将应用及其依赖打包到一个轻量级、可移植的容器中,从而实现跨平台运行。Docker 采用 C/S 架构,服务端称为 Docker Daemon&a…...

做题笔记(ctfshow)
一。ctfshow web13 文件扫描 存在upload.php.bak <?php header("content-type:text/html;charsetutf-8");$filename $_FILES[file][name];$temp_name $_FILES[file][tmp_name];$size $_FILES[file][size];$error $_FILES[file][error];$arr pathinfo($fi…...

Linux 用户层 和 内核层锁的实现
目录 一、系统调用futex介绍1. 核心机制2. 常见操作3. 工作流程示例(互斥锁)4. 优势5. 注意事项6. 典型应用 二、Linux中用户态的锁和内核的锁不是同一个实现吗?2.1 本质区别2.2 用户态锁如何工作(以 pthread_mutex 为例ÿ…...
)
Android第十五次面试总结(第三方组件和adb命令)
Android 第三方组件转为系统组件核心流程 这通常是在进行 Android 系统定制(如 ROM 开发、固件制作)时完成,目的是让第三方应用拥有更高的权限和系统身份。主要过程如下: 核心准备:签名!赋予系统身份 …...

Agent短期记忆的几种持久化存储方式
今天给大家讲一下关于Agent长期对话的几种持久化存储方式,之前的文章给大家说过短期记忆和长期记忆,短期记忆基于InMemorySaver做checkpointer(检查点),短期记忆 (线程级持久性) 使代理能够跟踪…...

Git 常见操作
目录 1.git stash 2.合并多个commit 3. git commit -amend (后悔药) 4.版本回退 5.merge和rebase 6.cherry pick 7.分支 8.alias 1.git stash git-stash操作_git stash 怎么增加更改内容-CSDN博客 2.合并多个commit 通过git bash工具交互式操作。 1.查询commit的c…...

从 ClickHouse、Druid、Kylin 到 Doris:网易云音乐 PB 级实时分析平台降本增效
网易云音乐基于 Apache Doris 替换了早期架构中 Kylin、Druid、Clickhouse、Elasticsearch、HBase 等引擎,统一了实时分析架构,并广泛应用于广告实时数仓、日志平台和会员报表分析等典型场景中,带来导入性能提升 3~30 倍ÿ…...

隐函数 因变量确定标准
涉及多元隐函数求导法的逻辑本质:当我们对隐函数关系 F ( x , y , z ) 0 F(x, y, z) 0 F(x,y,z)0 使用偏导法求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z时,为什么「偏导」能确定谁是因变量?为什么只有当对 z z z 的偏导 F z…...

Facebook接入说明
Facebook 原生 Messenger 聊天消息接入到一洽对话中 1、创建 Facebook 主页 进入 https://www.facebook.com/pages/create 页面根据提示创建主页(如果已经有待用主页,可跳过) 2、授权对话权限 1、向您的一洽负责人获取 Facebook 授权链接 2、…...

Grafana 地图本土化方案:使用高德地图API平替GeoMap地图指南
[ 知识是人生的灯塔,只有不断学习,才能照亮前行的道路 ] 📢 大家好,我是 WeiyiGeek,一名深耕安全运维开发(SecOpsDev)领域的技术从业者,致力于探索DevOps与安全的融合(De…...

Python爬虫实战:研究demiurge框架相关技术
1. 引言 在当今数字化时代,互联网上蕴含着海量的有价值信息。爬虫技术作为获取这些信息的重要手段,被广泛应用于学术研究、商业分析、舆情监测等多个领域。然而,构建一个高效、稳定且可维护的爬虫系统面临诸多挑战,如网页结构复杂多变、反爬机制日益严格、数据处理流程繁琐…...

3 个优质的终端 GitHub 开源工具
1、Oh My Zsh Oh My Zsh 是一个帮助你管理和美化 zsh 终端的开源工具。它让你的终端更炫酷、更高效。安装后,你可以快速使用各种插件和主题,比如常见的 git 命令简化、支持多种编程语言工具等,每次打开终端都会有惊喜。无论你是开发者还是普…...
 = 0 隐函数微分 确定自变量)
F(x, y, z) = 0 隐函数微分 确定自变量
多元隐函数偏导的通用公式: 设一个隐函数由三元函数定义: F ( x , y , z ) 0 F(x, y, z) 0 F(x,y,z)0 且假设 z z ( x , y ) z z(x, y) zz(x,y),即 z z z 是 x , y x, y x,y 的函数,满足这个等式恒成立。则有以下公式&am…...

亚马逊AWS云服务器高效使用指南:最大限度降低成本的实战策略
对于初次接触云计算的企业或个人开发者而言,亚马逊云服务器(Amazon EC2)的配置与成本控制往往面临双重挑战:既要理解数百种实例规格的技术参数,又要避免因配置不当导致的资源浪费。本文将深入剖析AWS EC2的核心使用场景…...

Android设备推送traceroute命令进行网络诊断
文章目录 工作原理下载traceroute for android推送到安卓设备执行traceroutetraceroute www.baidu.com Traceroute(追踪路由) 是一个用于网络诊断的工具,主要用于追踪数据包从源主机到目标主机所经过的路由路径,以及每一跳&#x…...
