2025年全国I卷数学压轴题解答
第19题第3问: b b b 使得存在 t t t, 对于任意的 x x x, 5 cos x − cos ( 5 x + t ) < b 5\cos x-\cos(5x+t)<b 5cosx−cos(5x+t)<b, 求 b b b 的最小值.
解:
b b b 的最小值 b m i n = min t max x g ( x , t ) b_{min}=\min_{t} \max_{x} g(x,t) bmin=mintmaxxg(x,t), 其中 g ( x , t ) = 5 cos x − cos ( 5 x + t ) g(x,t)=5\cos x-\cos (5x+t) g(x,t)=5cosx−cos(5x+t).
下面先求解 max x g ( x , t ) \max_{x} g(x,t) maxxg(x,t).
构造关于变元 x x x 的辅助函数 h ( x ) = g ( x , t ) h(x)=g(x,t) h(x)=g(x,t).
则 max x g ( x , t ) = max x h ( x ) \max_{x} g(x,t)=\max_{x} h(x) maxxg(x,t)=maxxh(x).
h ′ ( x ) = − 5 sin x + 5 sin ( 5 x + t ) h'(x)=-5\sin x+5\sin (5x+t) h′(x)=−5sinx+5sin(5x+t).
求解以下方程得到极值点:
2 k π + x = 5 x + t 2k\pi+x=5x+t 2kπ+x=5x+t, k ∈ Z k\in \mathbb{Z} k∈Z.
x = 2 k π − t 4 x=\frac{2k\pi-t}{4} x=42kπ−t.
( 2 k + 1 ) π − x = 5 x + t (2k+1)\pi-x=5x+t (2k+1)π−x=5x+t.
x = ( 2 k + 1 ) π − t 6 x=\frac{(2k+1)\pi-t}{6} x=6(2k+1)π−t.
显然 h ( x ) h(x) h(x) 的图像以 2 π 2\pi 2π 为周期, 且满足性质 h ( x ) = − h ( x + π ) h(x)=-h(x+\pi) h(x)=−h(x+π), 所以它的每个极大值的相反数必然是极小值, 反之亦然. 对负的极值取相反数就得到一个正的极值. 由此得到:
max x h ( x ) = max { max k ∣ 5 cos ( k π 2 − t 4 ) − cos ( 5 k π 2 − t 4 ) ∣ , max k ∣ 5 cos ( ( 2 k + 1 ) π 6 − t 6 ) − cos ( ( 10 k + 5 ) π 6 + t 6 ) ∣ } \max_{x} h(x)=\max \{\max_{k}|5 \cos (\frac{k\pi}{2}-\frac{t}{4}) - \cos (\frac{5k\pi}{2}-\frac{t}{4})|, \max_{k} |5 \cos (\frac{(2k+1)\pi}{6} - \frac{t}{6}) - \cos (\frac{(10k+5)\pi}{6}+\frac{t}{6})|\} maxxh(x)=max{maxk∣5cos(2kπ−4t)−cos(25kπ−4t)∣,maxk∣5cos(6(2k+1)π−6t)−cos(6(10k+5)π+6t)∣}
其中:
5 cos ( k π 2 − t 4 ) − cos ( 5 k π 2 − t 4 ) = 4 cos ( k π 2 − t 4 ) 5 \cos (\frac{k\pi}{2}-\frac{t}{4})- \cos (\frac{5k\pi}{2}-\frac{t}{4}) =4 \cos (\frac{k\pi}{2}-\frac{t}{4}) 5cos(2kπ−4t)−cos(25kπ−4t)=4cos(2kπ−4t),
cos ( ( 10 k + 5 ) π 6 + t 6 ) = cos ( ( − 10 k − 5 ) π 6 − t 6 ) = − cos ( ( − 10 k − 5 ) π 6 − t 6 + ( 2 k + 1 ) π ) = − cos ( ( 2 k + 1 ) π 6 − t 6 ) \cos (\frac{(10k+5)\pi}{6}+\frac{t}{6}) = \cos (\frac{(-10k-5)\pi}{6}-\frac{t}{6})=-\cos (\frac{(-10k-5)\pi}{6}-\frac{t}{6}+(2k+1)\pi)=-\cos(\frac{(2k+1)\pi}{6}-\frac{t}{6}) cos(6(10k+5)π+6t)=cos(6(−10k−5)π−6t)=−cos(6(−10k−5)π−6t+(2k+1)π)=−cos(6(2k+1)π−6t).
5 cos ( ( 2 k + 1 ) π 6 − t 6 ) − cos ( ( 10 k + 5 ) π 6 + t 6 ) = 6 cos ( ( 2 k + 1 ) π 6 − t 6 ) 5 \cos (\frac{(2k+1)\pi}{6} - \frac{t}{6}) - \cos (\frac{(10k+5)\pi}{6}+\frac{t}{6})=6\cos (\frac{(2k+1)\pi}{6} - \frac{t}{6}) 5cos(6(2k+1)π−6t)−cos(6(10k+5)π+6t)=6cos(6(2k+1)π−6t).
所以 max x g ( x , t ) = max x h ( x ) = max { max k ∣ 4 cos ( k π 2 − t 4 ) ∣ , max k ∣ 6 cos ( ( 2 k + 1 ) π 6 − t 6 ) ∣ } \max_{x}g(x,t)=\max_{x} h(x)=\max \{\max_{k}|4 \cos (\frac{k\pi}{2}-\frac{t}{4}) |, \max_{k} |6 \cos (\frac{(2k+1)\pi}{6} - \frac{t}{6})|\} maxxg(x,t)=maxxh(x)=max{maxk∣4cos(2kπ−4t)∣,maxk∣6cos(6(2k+1)π−6t)∣}.
下面求解: max t max x g ( x , t ) \max_{t} \max_{x}g(x,t) maxtmaxxg(x,t).
其中:
max k ∣ 6 cos ( ( 2 k + 1 ) π 6 − t 6 ) ∣ = max k = − 1 , 0 , 1 ∣ 6 cos ( ( 2 k + 1 ) π 6 − t 6 ) ∣ = 6 max { ∣ cos − π − t 6 ∣ , ∣ cos π − t 6 ∣ , ∣ cos 3 π − t 6 ∣ } \max_{k} |6 \cos (\frac{(2k+1)\pi}{6} - \frac{t}{6})|=\max_{k=-1,0,1}|6 \cos (\frac{(2k+1)\pi}{6} - \frac{t}{6})|=6\max\{|\cos\frac{-\pi-t}{6}|, |\cos\frac{\pi-t}{6}|, |\cos\frac{3\pi-t}{6}|\} maxk∣6cos(6(2k+1)π−6t)∣=maxk=−1,0,1∣6cos(6(2k+1)π−6t)∣=6max{∣cos6−π−t∣,∣cos6π−t∣,∣cos63π−t∣}.
构造关于变元 x x x 的辅助函数 g ( x ) = max { ∣ cos ( x − π 3 ) ∣ , ∣ cos x ∣ , ∣ cos ( x + π 3 ) ∣ } g(x)=\max\{|\cos (x-\frac{\pi}{3})|, |\cos x|, |\cos (x+\frac{\pi}{3})|\} g(x)=max{∣cos(x−3π)∣,∣cosx∣,∣cos(x+3π)∣}, 结合图像可知 g ( x ) ≥ 3 2 g(x)\geq \frac{\sqrt{3}}{2} g(x)≥23, 当 x = π 6 x=\frac{\pi}{6} x=6π 时等号成立.
所以 max { ∣ cos π − t 6 ∣ , ∣ cos 3 π − t 6 ∣ } ≤ 3 2 \max\{|\cos\frac{\pi-t}{6}|, |\cos\frac{3\pi-t}{6}|\} \leq \frac{\sqrt{3}}{2} max{∣cos6π−t∣,∣cos63π−t∣}≤23, 当 π − t 6 = π 6 \frac{\pi-t}{6}=\frac{\pi}{6} 6π−t=6π, 即 t = 0 t=0 t=0 时等号成立.
∣ 4 cos ( k π 2 − t 4 ) ∣ ≤ 4 < 3 3 |4 \cos (\frac{k\pi}{2}-\frac{t}{4})|\leq 4<3\sqrt{3} ∣4cos(2kπ−4t)∣≤4<33.
综上, max t max x g ( x , t ) = 3 3 \max_{t} \max_{x}g(x,t)=3\sqrt{3} maxtmaxxg(x,t)=33.
相关文章:

2025年全国I卷数学压轴题解答
第19题第3问: b b b 使得存在 t t t, 对于任意的 x x x, 5 cos x − cos ( 5 x t ) < b 5\cos x-\cos(5xt)<b 5cosx−cos(5xt)<b, 求 b b b 的最小值. 解: b b b 的最小值 b m i n min t max x g ( x , t ) b_{min}\min_{t} \max_{x} g(x,t) bmi…...
: 发布订阅模式)
JS设计模式(5): 发布订阅模式
解锁JavaScript发布订阅模式:让代码沟通更优雅 在JavaScript的世界里,我们常常会遇到这样的场景:多个模块之间需要相互通信,但是又不想让它们产生过于紧密的耦合。这时候,发布订阅模式就像一位优雅的信使,…...

实现p2p的webrtc-srs版本
1. 基本知识 1.1 webrtc 一、WebRTC的本质:实时通信的“网络协议栈”类比 将WebRTC类比为Linux网络协议栈极具洞察力,二者在架构设计和功能定位上高度相似: 分层协议栈架构 Linux网络协议栈:从底层物理层到应用层(如…...
)
Android多媒体——音/视频数据播放(十八)
在媒体数据完成解码并准备好之后,播放流程便进入了最终的呈现阶段。为了确保音视频内容能够顺利输出,系统需要首先对相应的播放设备进行初始化。只有在设备初始化成功后,才能真正开始音视频的同步渲染与播放。这一过程不仅影响播放的启动速度,也直接关系到播放的稳定性和用…...

第2篇:BLE 广播与扫描机制详解
本文是《BLE 协议从入门到专家》专栏第二篇,专注于解析 BLE 广播(Advertising)与扫描(Scanning)机制。我们将从协议层结构、广播包格式、设备发现流程、控制器行为、开发者 API、广播冲突与多设备调度等方面,全面拆解这一 BLE 最基础也是最关键的通信机制。 一、什么是 B…...

开源 vGPU 方案:HAMi,实现细粒度 GPU 切分
本文主要分享一个开源的 GPU 虚拟化方案:HAMi,包括如何安装、配置以及使用。 相比于上一篇分享的 TimeSlicing 方案,HAMi 除了 GPU 共享之外还可以实现 GPU core、memory 得限制,保证共享同一 GPU 的各个 Pod 都能拿到足够的资源。…...

EC2安装WebRTC sdk-c环境、构建、编译
1、登录新的ec2实例,证书可以跟之前的实例用一个: ssh -v -i ~/Documents/cert/qa.pem ec2-user70.xxx.165.xxx 2、按照sdk-c demo中readme的描述开始安装环境: https://github.com/awslabs/amazon-kinesis-video-streams-webrtc-sdk-c 2…...

盲盒一番赏小程序:引领盲盒新潮流
在盲盒市场日益火爆的今天,如何才能在众多盲盒产品中脱颖而出?盲盒一番赏小程序给出了答案,它以创新的玩法和优质的服务,引领着盲盒新潮流。 一番赏小程序的最大特色在于其独特的赏品分级制度。赏品分为多个等级,从普…...

边缘计算设备全解析:边缘盒子在各大行业的落地应用场景
随着工业物联网、AI、5G的发展,数据量呈爆炸式增长。但你有没有想过,我们生成的数据,真的都要发回云端处理吗?其实不一定。特别是在一些对响应时间、网络带宽、数据隐私要求高的行业里,边缘计算开始“火”了起来&#…...

Linux实现线程同步的方式有哪些?
什么是线程同步? 想象一下超市收银台:如果所有顾客(线程)同时挤向同一个收银台(共享资源),场面会一片混乱。线程同步就是给顾客们发"排队号码牌",确保: 有序访…...

python打卡day47
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import D…...

python学习day39
图像数据与显存 知识点回顾 1.图像数据的格式:灰度和彩色数据 2.模型的定义 3.显存占用的4种地方 a.模型参数梯度参数 b.优化器参数 c.数据批量所占显存 d.神经元输出中间状态 4.batchisize和训练的关系 import torch import torchvision import torch.nn as nn imp…...

Ansible+Zabbix-agent2快速实现对多主机监控
ansible Ansible 是一款开源的自动化工具,用于配置管理(Configuration Management)、应用部署(Application Deployment)、任务自动化(Task Automation)和编排(Orchestration…...

年度峰会上,抖音依靠人工智能和搜索功能吸引广告主
上周早些时候举行的第五届年度TikTok World产品峰会上,TikTok推出了一系列旨在增强该应用对广告主吸引力的功能。 新产品列表的首位是TikTok Market Scope,这是一个全新的分析平台,为广告主提供整个考虑漏斗的全面视图,使他们能够…...

Vuex:Vue.js 应用程序的状态管理模式
什么是Vuex? Vuex 是专门为 Vue.js 应用程序开发的状态管理模式 库。它采用集中式存储管理应用的所有组件的状态,并以相应的规则保证状态以一种可预测的方式发生变化。 在大型单页应用中,当多个组件共享状态时,简单的单向数据流…...

【中间件】Web服务、消息队列、缓存与微服务治理:Nginx、Kafka、Redis、Nacos 详解
Nginx 是什么:高性能的HTTP和反向代理Web服务器。怎么用:通过配置文件定义代理规则、负载均衡、静态资源服务等。为什么用:提升Web服务性能、高并发处理、负载均衡和反向代理。优缺点:轻量高效,但动态处理能力较弱&am…...

如何使用CodeRider插件在IDEA中生成代码
一、环境搭建与插件安装 1.1 环境准备 名称要求说明操作系统Windows 11JetBrains IDEIntelliJ IDEA 2025.1.1.1 (Community Edition)硬件配置推荐16GB内存50GB磁盘空间 1.2 插件安装流程 步骤1:市场安装 打开IDEA,进入File → Settings → Plugins搜…...

电脑定时关机工具推荐
软件介绍 本文介绍一款轻量级的电脑自动关机工具,无需安装,使用简单,可满足定时关机需求。 工具简介 这款关机助手是一款无需安装的小型软件,文件体积仅60KB,下载后可直接运行,无需复杂配置。 使用…...

Ubuntu 可执行程序自启动方法
使用 autostart(适用于桌面环境) 适用于 GNOME/KDE 桌面环境(如 Ubuntu 图形界面) 1. 创建 .desktop 文件 sudo vi ~/.config/autostart/my_laser.desktop[Desktop Entry] TypeApplication NameMy Laser Program Execbash -c &…...

Springboot多数据源配置实践
Springboot多数据源配置实践 基本配置文件数据库配置Mapper包Model包Service包中业务代码Mapper XML文件在某些复杂的业务场景中,我们可能需要使用多个数据库来存储和管理不同类型的数据,而不是仅仅依赖于单一数据库。本技术文档将详细介绍如何在 Spring Boot 项目中进行多数…...

第6章:Neo4j数据导入与导出
在实际应用中,数据的导入与导出是使用Neo4j的重要环节。无论是初始数据加载、系统迁移还是数据备份,都需要高效可靠的数据传输机制。本章将详细介绍Neo4j中的各种数据导入与导出方法,帮助读者掌握不同场景下的最佳实践。 6.1 数据导入策略 …...

uni-app学习笔记二十三--交互反馈showToast用法
showToast部分文档位于uniapp官网-->API-->界面:uni.showToast(OBJECT) | uni-app官网 uni.showToast(OBJECT) 用于显示消息提示框 OBJECT参数说明 参数类型必填说明平台差异说明titleString是提示的内容,长度与 icon 取值有关。iconString否图…...

Go爬虫开发学习记录
Go爬虫开发学习记录 基础篇:使用net/http库 Go的标准库net/http提供了完善的HTTP客户端功能,是构建爬虫的基石: package mainimport ("fmt""io""net/http" )func fetchPage(url string) string {// 创建自定…...

前端异步编程全场景解读
前端异步编程是现代Web开发的核心,它解决了浏览器单线程执行带来的UI阻塞问题。以下从多个维度进行深度解析: 一、异步编程的核心概念 JavaScript的执行环境是单线程的,这意味着在同一时间只能执行一个任务。为了不阻塞主线程,J…...

分布式光纤声振传感技术原理与瑞利散射机制解析
分布式光纤传感技术(Distributed Fiber Optic Sensing,简称DFOS)作为近年来迅速发展的新型感知手段,已广泛应用于边界安防、油气管道监测、结构健康诊断、地震探测等领域。其子类技术——分布式光纤声振传感(Distribut…...
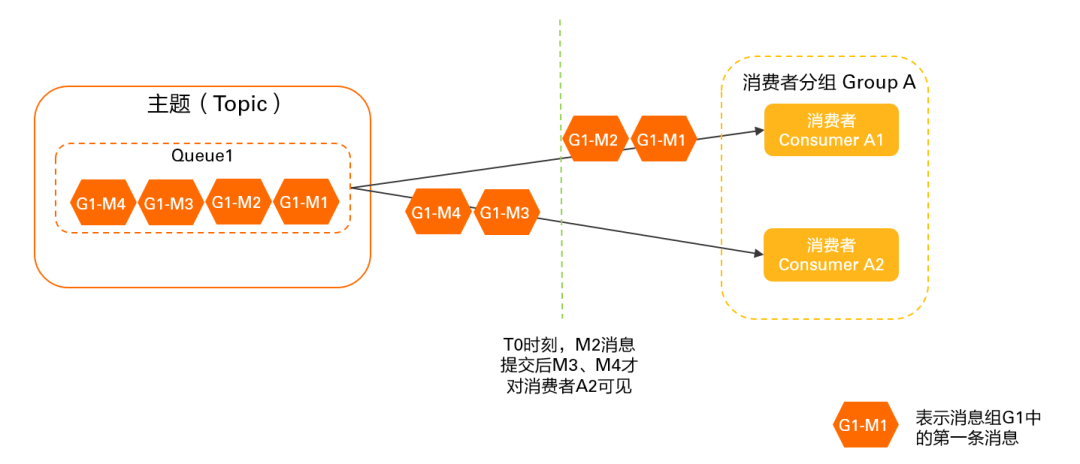
RocketMQ 客户端负载均衡机制详解及最佳实践
延伸阅读:🔍「RocketMQ 中文社区」 持续更新源码解析/最佳实践,提供 RocketMQ 专家 AI 答疑服务 前言 本文介绍 RocketMQ 负载均衡机制,主要涉及负载均衡发生的时机、客户端负载均衡对消费的影响(消息堆积/消费毛刺等…...

Q1起重机指挥理论备考要点分析
Q1起重机指挥理论备考要点分析 一、考试重点内容概述 Q1起重机指挥理论考试主要包含三大核心模块:安全技术知识(占40%)、指挥信号规范(占30%)和法规标准(占30%)。考试采用百分制,8…...

c++算法学习3——深度优先搜索
一、深度优先搜索的核心概念 DFS算法是一种通过递归或栈实现的"一条路走到底"的搜索策略,其核心思想是: 深度优先:从起点出发,选择一个方向探索到底,直到无路可走 回溯机制:遇到死路时返回最近…...

如何让非 TCP/IP 协议驱动屏蔽 IPv4/IPv6 和 ARP 报文?
——从硬件过滤到协议栈隔离的完整指南 引言 在现代网络开发中,许多场景需要定制化网络协议(如工业控制、高性能计算),此时需确保驱动仅处理特定协议,避免被标准协议(如 IPv4/IPv6/ARP)干扰。本文基于 Linux 内核驱动的实现,探讨如何通过硬件过滤、驱动层拦截和协议栈…...

组合模式:构建树形结构的艺术
引言:处理复杂对象结构的挑战 在软件开发中,我们常遇到需要处理部分-整体层次结构的场景: 文件系统中的文件与文件夹GUI中的容器与组件组织结构中的部门与员工菜单系统中的子菜单与菜单项组合模式正是为解决这类问题而生的设计模式。它允许我们将对象组合成树形结构来表示&…...
