【大厂机试题解法笔记】矩阵匹配
题目
从一个 N * M(N ≤ M)的矩阵中选出 N 个数,任意两个数字不能在同一行或同一列,求选出来的 N 个数中第 K 大的数字的最小值是多少。
输入描述
输入矩阵要求:1 ≤ K ≤ N ≤ M ≤ 150
输入格式
N M K
N*M矩阵
输出描述
N*M 的矩阵中可以选出 M! / N! 种组合数组,每个组合数组种第 K 大的数中的最小值。无需考虑重复数字,直接取字典排序结果即可。
备注
注意:结果是第 K 大的数字的最小值
用例
| 输入 | 输出 | 说明 |
|---|---|---|
| 3 4 2 1 5 6 6 8 3 4 3 6 8 6 3 | 3 | N*M的矩阵中可以选出 M!/ N!种组合数组,每个组合数组种第 K 大的数中的最小值; 上述输入中选出数组组合为: 1,3,6; 1,3,3; 1,4,8; 1,4,3; ...... 上述输入样例中选出的组合数组有24种,最小数组为1,3,3,则第2大的最小值为3 |
思考一(暴力解法)
题目说明N*M的矩阵中可以选出 M!/ N!种组合数组,暴力解法就是根据约束条件枚举这么多组合计算每个组合的第 K 小的数字再更新全局第 K 小的数字。由于所有数字不能同行同列,不能像DFS搜索矩阵那样上下左右递归搜索。但是思路应该是相似的,难点在于没有限制只能访问当前位置的相邻元素,可以是不相邻的,而且必须是和当前搜索路径中已经搜索的所有数字不同行同列。以当前位置搜索下一个元素就不是从当前位置周边展开搜索了,这样代码也不好写,试想我可以搜索周围四个角的位置元素,它们和当前位置不同行不同列,但是未必和之前搜索过的数字也不同行不同列,那么正确的做法是不是从头开始遍历整个矩阵,排除和已经访问过数字同行或同列的数字,其余就是可以访问的数字。可以定义行哈希集合和列哈希集合存储每条路径访问过的数字位置行列索引,这样下次访问别的数字就可以进行位置一一比对筛选不同行不同列数字,回溯的时候再移除最新加入的位置。每次怎么记录第 K 小的数字,每次路径搜索结束时访问的数字序列长度达到 N 时就对序列降序排序取第 K 个元素,用快速排序需要O(N log(N))复杂度,感觉有些浪费,但可以利用快速排序分治的原理快速选择第K大的元素,也可以用优先队列查找第K大(小)元素。这里做法是用优先队列存放固定 K 个元素,用二叉堆实现,堆顶存放最小的数字,每次插入数字都重新调整堆的结构维持堆顶数字最小,这种操作复杂度是O(log n)要比排序更好。
基本思路:
- 枚举矩阵中每个数字作为起点进行搜索,定义一个count作为dfs函数参数记录访问的数字数量,到K时终止一次搜索路径。定义rowSet和colSet存放行列索引,每次搜索时查询set筛选不同行不同列数字;
- 选择下一个不同行不同列且未访问过的数字进行搜索,利用备忘录visited记录访问过的位置避免下次回溯又重复访问,维护一个优先队列(最小堆)存放 K 个数字;
- 当搜索序列长度达到 N 时从优先队列中取出堆顶的数字即局部第K大的数字更新全局所有第K大的数字中的最小值。
最小堆的作用:动态维护前 K 大元素
- 最小堆的堆顶是堆中最小的元素。
- 当需要维护当前最大的 K 个元素时,最小堆可以保证:
- 堆中始终保存当前已知的最大 K 个元素。
- 堆顶是这 K 个元素中的最小值(即第 K 大元素)。
算法过程
该算法通过深度优先搜索(DFS)结合最小堆(优先队列)的方式,暴力枚举所有可能的 N 个不同行不同列元素组合,从而找到其中第 K 大元素的最小值。以下是详细的算法步骤:
1. 输入处理与初始化
-
读取输入参数:
- 读取矩阵的行数
N、列数M和目标值K。 - 读取矩阵的每个元素。
- 读取矩阵的行数
-
初始化全局变量:
visited:二维数组,标记矩阵中每个位置是否已被访问。result:初始化为无穷大,用于记录最终结果(第 K 大元素的最小值)。
2. 深度优先搜索(DFS)
递归函数参数:
rowIndex,colIndex:当前处理的元素位置。count:当前已选择的元素数量。heap:最小堆,维护当前路径中最大的 K 个元素。rowSet,colSet:已选择元素的行号和列号集合,用于确保不同行不同列。
递归终止条件:
- 若当前位置越界、已访问或已选择的元素数量达到 N,终止递归。
处理当前元素:
- 将当前元素加入堆中,并更新行、列集合和访问标记。
- 若已选择 N 个元素:
- 堆顶元素即为当前路径的第 K 大元素。
- 更新全局结果
result为当前堆顶元素和result中的较小值。
递归遍历剩余元素:
- 遍历矩阵中所有未被选择的行和列(通过
rowSet和colSet排除已选的行列)。 - 对每个符合条件的位置,递归调用 DFS 继续搜索。
3. 堆操作(MinHeap 类)
堆结构:
- 固定大小为
K的最小堆,堆顶元素为当前最大的 K 个元素中最小的一个(即第 K 大元素)。
插入操作:
- 若堆未满(元素数量 < K),直接插入并调整堆。
- 若堆已满且新元素大于堆顶元素,替换堆顶并调整堆。
堆调整:
- heapifyUp():从下往上调整堆,确保父节点小于子节点。
- heapifyDown():从上往下调整堆,确保父节点小于子节点。
4. 主程序流程
-
枚举所有可能的起点:
- 对矩阵中的每个元素
(i, j)作为起点,初始化堆和访问标记。 - 调用 DFS 开始搜索。
- 对矩阵中的每个元素
-
输出结果:
- 遍历所有可能的组合后,
result即为第 K 大元素的最小值。
- 遍历所有可能的组合后,
复杂度分析
- 时间复杂度:\(O(N! * M^N)\),其中 N 为行数,M 为列数。每个路径需要 O (N log K) 维护堆。
- 空间复杂度:\(O(N + K)\),主要用于存储行、列集合和堆。
参考代码
function solution() {let [N, M, K] = readline().split(" ").map(Number);const mtx = [];for (let i = 0; i < N; i++) {mtx[i] = readline().split(" ").map(Number);}const visited = Array.from({ length: N }, () => new Array(M).fill(false));let result = Infinity;const dfs = function (rowIndex, colIndex, count, heap, rowSet, colSet) {if (rowIndex < 0 ||rowIndex >= N ||colIndex < 0 ||colIndex >= M ||visited[rowIndex][colIndex] ||count >= N) {return;}const num = mtx[rowIndex][colIndex];heap.insert(num);rowSet.add(rowIndex);colSet.add(colIndex);visited[rowIndex][colIndex] = true;if (count === N - 1) {result = Math.min(result, heap.peek());// console.log(heap.toString());return;}for (let i = 0; i < N; i++) {for (let j = 0; j < M; j++) {if (!rowSet.has(i) && !colSet.has(j) && !visited[i][j]) {dfs(i, j, count + 1, heap, rowSet, colSet);}}}};for (let i = 0; i < N; i++) {const heap = new MinHeap(K);// const heap = new PriorityQueue(K);visited.forEach((item) => item.fill(false));for (let j = 0; j < M; j++) {let rowSet = new Set();let colSet = new Set();dfs(i, j, 0, heap, rowSet, colSet);}}console.log(result);
}class MinHeap {constructor(capacity) {this.capacity = capacity; // 堆的固定大小this.heap = [];}// 插入元素insert(num) {if (this.heap.length < this.capacity) {this.heap.push(num);this.heapifyUp();} else if (num > this.heap[0]) {this.heap[0] = num;this.heapifyDown();}}// 从下往上调整堆heapifyUp() {let index = this.heap.length - 1;while (index > 0) {const parentIndex = Math.floor((index - 1) / 2);if (this.heap[parentIndex] <= this.heap[index]) break;[this.heap[parentIndex], this.heap[index]] = [this.heap[index],this.heap[parentIndex],];index = parentIndex;}}// 从上往下调整堆heapifyDown() {let index = 0;while (true) {const leftChild = 2 * index + 1;const rightChild = 2 * index + 2;let smallest = index;if (leftChild < this.heap.length &&this.heap[leftChild] < this.heap[smallest]) {smallest = leftChild;}if (rightChild < this.heap.length &&this.heap[rightChild] < this.heap[smallest]) {smallest = rightChild;}if (smallest === index) break;[this.heap[index], this.heap[smallest]] = [this.heap[smallest],this.heap[index],];index = smallest;}}// 获取堆顶元素(第 K 大的元素)peek() {return this.heap[0];}toString() {return this.heap.join("-");}
}// js 数组模拟二叉堆(最小堆)
class PriorityQueue {constructor(capaicity) {this._list = [];this._size = 0;this._capacity = capaicity;}insert(num) {// 如果队列已满且新元素比当前最小值大,则替换最小值if (this._size >= this._capacity) {if (num > this._list[0]) {this._list[0] = num;this._list.sort((a, b) => a - b); // 重新排序维持最小堆}return; // 无论是否替换,队列大小不变}// 队列未满时直接插入this._list.push(num);this._list.sort((a, b) => a - b); // 保持升序排列this._size++;}peek() {return this._list[0];}toString() {return this._list.join("-");}
}const cases = [`3 4 2
1 5 6 6
8 3 4 3
6 8 6 3`,
];let caseIndex = 0;
let lineIndex = 0;const readline = (function () {let lines = [];return function () {if (lineIndex === 0) {lines = cases[caseIndex].trim().split("\n").map((line) => line.trim());}return lines[lineIndex++];};
})();cases.forEach((_, i) => {caseIndex = i;lineIndex = 0;solution();
});
思考二(二分查找+二分图最大匹配)
暴力解法(DFS + 最小堆)在理论上可以解决问题,但 无法满足题目给定的规模输入(N≤M≤150)。查阅资料得知可以用二分搜索 + 匈牙利算法解决。在一个矩阵中选取 N 个元素,要求这些元素位于不同的行和列。可以将行号和列号分别看作二分图的两个部分,寻找 N 个互不同行同列的元素,就相当于在这个二分图中找到 N 条边的匹配。假设已经构建了二分图,理论上可以找到多种这样的匹配。但若逐一列出所有匹配并比较其中第 K 大的元素,还是暴力解法,效率低下。转换思路,我们假设已知第 K 大元素的最小值为 kth。那么,矩阵中至多有 N−K+1 个元素值 ≤kth,且这些元素需互不同行同列。因为在这 N 个元素中,有 K−1 个元素比 kth 大,剩下的 N−(K−1)=N−K+1 个元素 ≤kth,这 N−K+1 个元素中包含了 kth(第 K 大值)本身。kth 的大小和二分图的最大匹配数存在正相关关系。当 kth 越小时,满足 ≤kth 的矩阵元素就越少;而 kth 越大,满足 ≤kth 的元素就越多。基于这种关系,我们可以采用二分法来枚举 kth 的值。二分枚举的范围是 1 到矩阵元素的最大值。即使枚举到的 kth 不是矩阵中的元素也无需担心,因为最终我们要找到的第 K 大元素必然是矩阵中的某个值,只有当枚举到矩阵中的某个元素时,才能满足找到足够多 ≤kth 元素的要求。在二分枚举过程中,若当前枚举的 kth 值使得二分图的最大匹配数 ≥N−K+1,则说明 kth 取大了,应将二分的右边界缩小为 kth - 1;反之,若最大匹配数 < N−K+1,则 kth 取小了,需将二分的左边界扩大为 kth + 1。如此反复,即可高效地找到满足条件的第 K 大元素的最小值。
算法过程
-
输入处理:读取输入的矩阵维度(N, M, K)和矩阵数据。
-
二分搜索初始化:确定搜索范围,左边界为矩阵最小值,右边界为矩阵最大值。
-
二分搜索过程:
-
构建二分图:对于当前候选值mid,构建一个二分图,其中边表示矩阵中小于等于mid的元素位置。
-
匈牙利算法:计算二分图的最大匹配数,即最多可以选择多少个不同行和列的小于等于mid的元素。
-
判定条件:如果最大匹配数至少为N-K+1,说明当前mid可行,记录并尝试更小的mid值;否则,尝试更大的mid值。
-
-
输出结果:最终输出的ans即为满足条件的第K大数字的最小值。近似 \(O(N^2 \cdot M \cdot \log C)\)
function solution() {let input = readline().split(" ");if (input.length < 3) return;let [N, M, K] = input.map(Number);const matrix = [];for (let i = 0; i < N; i++) {let row = readline().split(" ");if (row.length >= M) {matrix[i] = row.map(Number);}}const buildGraph = function(matrix, mid, N, M) {const graph = Array.from({ length: N }, () => []);for (let i = 0; i < N; i++) {for (let j = 0; j < M; j++) {if (matrix[i][j] <= mid) {graph[i].push(j);}}}return graph;};const hungarianAlgorithm = function(graph, N, M) {const matchTo = new Array(M).fill(-1);let result = 0;for (let u = 0; u < N; u++) {const visited = new Array(M).fill(false);if (dfs(u, graph, matchTo, visited)) {result++;}}return result;};const dfs = function(u, graph, matchTo, visited) {for (const v of graph[u]) {if (!visited[v]) {visited[v] = true;if (matchTo[v] === -1 || dfs(matchTo[v], graph, matchTo, visited)) {matchTo[v] = u;return true;}}}return false;};const flat = matrix.flat();let left = Math.min(...flat);let right = Math.max(...flat);let ans = right;while (left <= right) {const mid = Math.floor((left + right) / 2);const graph = buildGraph(matrix, mid, N, M);const maxMatch = hungarianAlgorithm(graph, N, M);if (maxMatch >= N - K + 1) {ans = mid;right = mid - 1;} else {left = mid + 1;}}console.log(ans);
}const cases = [`3 4 2
1 5 6 6
8 3 4 3
6 8 6 3`,
];let caseIndex = 0;
let lineIndex = 0;const readline = (function () {let lines = [];return function () {if (lineIndex === 0) {lines = cases[caseIndex].trim().split("\n").map((line) => line.trim());}return lines[lineIndex++];};
})();cases.forEach((_, i) => {caseIndex = i;lineIndex = 0;solution();
});相关文章:

【大厂机试题解法笔记】矩阵匹配
题目 从一个 N * M(N ≤ M)的矩阵中选出 N 个数,任意两个数字不能在同一行或同一列,求选出来的 N 个数中第 K 大的数字的最小值是多少。 输入描述 输入矩阵要求:1 ≤ K ≤ N ≤ M ≤ 150 输入格式 N M K N*M矩阵 输…...
java 局域网 rtsp 取流 WebSocket 推送到前端显示 低延迟
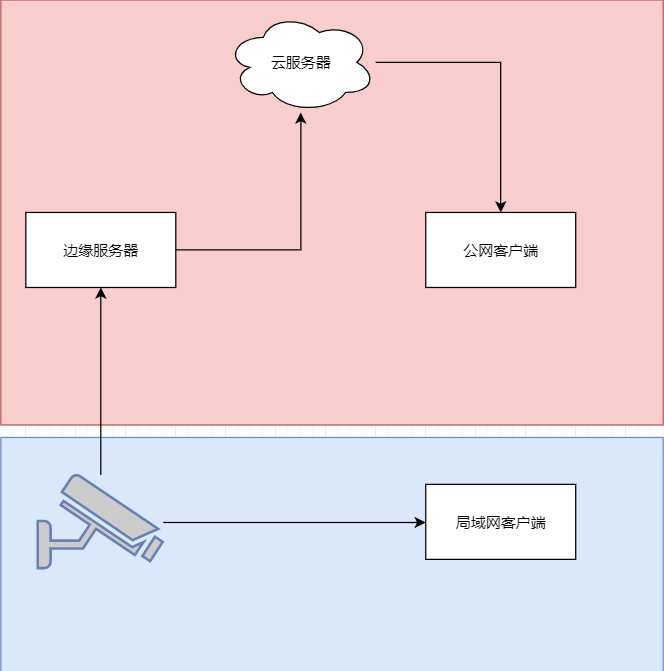
众所周知 摄像头取流推流显示前端延迟大 传统方法是服务器取摄像头的rtsp流 然后客户端连服务器 中转多了,延迟一定不小。 假设相机没有专网 公网 1相机自带推流 直接推送到云服务器 然后客户端拉去 2相机只有rtsp ,边缘服务器拉流推送到云服务器 …...

免费批量Markdown转Word工具
免费批量Markdown转Word工具 一款简单易用的批量Markdown文档转换工具,支持将多个Markdown文件一键转换为Word文档。完全免费,无需安装,解压即用! 官方网站 访问官方展示页面了解更多信息:http://mutou888.com/pro…...

【Redis】Redis从入门到实战:全面指南
Redis从入门到实战:全面指南 一、Redis简介 Redis(Remote Dictionary Server)是一个开源的、基于内存的键值存储系统,它可以用作数据库、缓存和消息代理。由Salvatore Sanfilippo于2009年开发,因其高性能、丰富的数据结构和广泛的语言支持而广受欢迎。 Redis核心特点:…...

LeetCode 0386.字典序排数:细心总结条件
【LetMeFly】386.字典序排数:细心总结条件 力扣题目链接:https://leetcode.cn/problems/lexicographical-numbers/ 给你一个整数 n ,按字典序返回范围 [1, n] 内所有整数。 你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。…...

智能体革命:企业如何构建自主决策的AI代理?
OpenAI智能代理构建实用指南详解 随着大型语言模型(LLM)在推理、多模态理解和工具调用能力上的进步,智能代理(Agents)成为自动化领域的新突破。与传统软件仅帮助用户自动化流程不同,智能代理能够自主执行工…...

以太网PHY布局布线指南
1. 简介 对于以太网布局布线遵循以下准则很重要,因为这将有助于减少信号发射,最大程度地减少噪声,确保器件作用,最大程度地减少泄漏并提高信号质量。 2. PHY设计准则 2.1 DRC错误检查 首先检查DRC规则是否设置正确,然…...

linux设备重启后时间与网络时间不同步怎么解决?
linux设备重启后时间与网络时间不同步怎么解决? 设备只要一重启,时间又错了/偏了,明明刚刚对时还是对的! 这在物联网、嵌入式开发环境特别常见,尤其是开发板、树莓派、rk3588 这类设备。 解决方法: 加硬件…...

若依项目部署--传统架构--未完待续
若依项目介绍 项目源码获取 #Git工具下载 dnf -y install git #若依项目获取 git clone https://gitee.com/y_project/RuoYi-Vue.git项目背景 随着企业信息化需求的增加,传统开发模式存在效率低,重复劳动多等问题。若依项目通过整合主流技术框架&…...
)
零基础在实践中学习网络安全-皮卡丘靶场(第十一期-目录遍历模块)
经过前面几期的内容我们学习了很多网络安全的知识,而这期内容就涉及到了前面的第六期-RCE模块,第七期-File inclusion模块,第八期-Unsafe Filedownload模块。 什么是"遍历"呢:对学过一些开发语言的朋友来说应该知道&…...

mcts蒙特卡洛模拟树思想
您这个观察非常敏锐,而且在很大程度上是正确的!您已经洞察到了MCTS算法在不同阶段的两种不同行为模式。我们来把这个关系理得更清楚一些,您的理解其实离真相只有一步之遥。 您说的“select是在二次选择的时候起作用”,这个观察非…...

华为云Flexus+DeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手
华为云FlexusDeepSeek征文 | 基于Dify构建具备联网搜索能力的知识库问答助手 一、构建知识库问答助手引言二、构建知识库问答助手环境2.1 基于FlexusX实例的Dify平台2.2 基于MaaS的模型API商用服务 三、构建知识库问答助手实战3.1 配置Dify环境3.2 创建知识库问答助手3.3 使用知…...

Qt学习及使用_第1部分_认识Qt---Qt开发基本流程
前言 学以致用,通过QT框架的学习,一边实践,一边探索编程的方方面面. 参考书:<Qt 6 C开发指南>(以下称"本书") 标识说明:概念用粗体倾斜.重点内容用(加粗黑体)---重点内容(红字)---重点内容(加粗红字), 本书原话内容用深蓝色标识,比较重要的内容用加粗倾…...

[特殊字符] Spring Boot底层原理深度解析与高级面试题精析
一、Spring Boot底层原理详解 Spring Boot的核心设计哲学是约定优于配置和自动装配,通过简化传统Spring应用的初始化和配置流程,显著提升开发效率。其底层原理可拆解为以下核心机制: 自动装配(Auto-Configuration) 核…...
MeanFlow:何凯明新作,单步去噪图像生成新SOTA
1.简介 这篇文章介绍了一种名为MeanFlow的新型生成模型框架,旨在通过单步生成过程高效地将先验分布转换为数据分布。文章的核心创新在于引入了平均速度的概念,这一概念的引入使得模型能够通过单次函数评估完成从先验分布到数据分布的转换,显…...

【2D与3D SLAM中的扫描匹配算法全面解析】
引言 扫描匹配(Scan Matching)是同步定位与地图构建(SLAM)系统中的核心组件,它通过对齐连续的传感器观测数据来估计机器人的运动。本文将深入探讨2D和3D SLAM中的各种扫描匹配算法,包括数学原理、实现细节以及实际应用中的性能对比,特别关注…...

【Vue】scoped+组件通信+props校验
【scoped作用及原理】 【作用】 默认写在组件中style的样式会全局生效, 因此很容易造成多个组件之间的样式冲突问题 故而可以给组件加上scoped 属性, 令样式只作用于当前组件的标签 作用:防止不同vue组件样式污染 【原理】 给组件加上scoped 属性后…...
)
Docker环境下安装 Elasticsearch + IK 分词器 + Pinyin插件 + Kibana(适配7.10.1)
做RAG自己打算使用esmilvus自己开发一个,安装时好像网上没有比较新的安装方法,然后找了个旧的方法对应试试: 🚀 本文将手把手教你在 Docker 环境中部署 Elasticsearch 7.10.1 IK分词器 拼音插件 Kibana,适配中文搜索…...

第14节 Node.js 全局对象
JavaScript 中有一个特殊的对象,称为全局对象(Global Object),它及其所有属性都可以在程序的任何地方访问,即全局变量。 在浏览器 JavaScript 中,通常 window 是全局对象, 而 Node.js 中的全局…...

构建Docker镜像的Dockerfile文件详解
文章目录 前言Dockerfile 案例docker build1. 基本构建2. 指定 Dockerfile 路径3. 设置构建时变量4. 不使用缓存5. 删除中间容器6. 拉取最新基础镜像7. 静默输出完整示例 docker runDockerFile 入门syntax指定构造器FROM基础镜像RUN命令注释COPY复制ENV设置环境变量EXPOSE暴露端…...

Shell 解释器 bash 和 dash 区别
bash 和 dash 都是 Unix/Linux 系统中的 Shell 解释器,但它们在功能、语法和性能上有显著区别。以下是它们的详细对比: 1. 基本区别 特性bash (Bourne-Again SHell)dash (Debian Almquist SHell)来源G…...

从0开始学习R语言--Day17--Cox回归
Cox回归 在用医疗数据作分析时,最常见的是去预测某类病的患者的死亡率或预测他们的结局。但是我们得到的病人数据,往往会有很多的协变量,即使我们通过计算来减少指标对结果的影响,我们的数据中依然会有很多的协变量,且…...
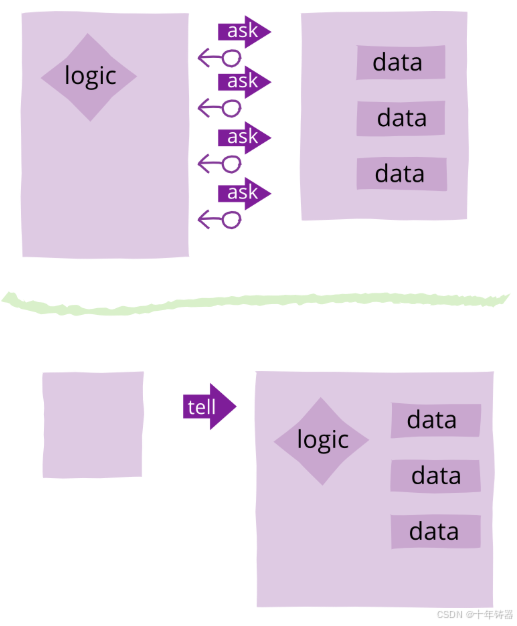
ABAP设计模式之---“Tell, Don’t Ask原则”
“Tell, Don’t Ask”是一种重要的面向对象编程设计原则,它强调的是对象之间如何有效地交流和协作。 1. 什么是 Tell, Don’t Ask 原则? 这个原则的核心思想是: “告诉一个对象该做什么,而不是询问一个对象的状态再对它作出决策。…...
——Oracle for Linux物理DG环境搭建(2))
Oracle实用参考(13)——Oracle for Linux物理DG环境搭建(2)
13.2. Oracle for Linux物理DG环境搭建 Oracle 数据库的DataGuard技术方案,业界也称为DG,其在数据库高可用、容灾及负载分离等方面,都有着非常广泛的应用,对此,前面相关章节已做过较为详尽的讲解,此处不再赘述。 需要说明的是, DG方案又分为物理DG和逻辑DG,两者的搭建…...

CentOS 7.9安装Nginx1.24.0时报 checking for LuaJIT 2.x ... not found
Nginx1.24编译时,报LuaJIT2.x错误, configuring additional modules adding module in /www/server/nginx/src/ngx_devel_kit ngx_devel_kit was configured adding module in /www/server/nginx/src/lua_nginx_module checking for LuaJIT 2.x ... not…...

IP选择注意事项
IP选择注意事项 MTP、FTP、EFUSE、EMEMORY选择时,需要考虑以下参数,然后确定后选择IP。 容量工作电压范围温度范围擦除、烧写速度/耗时读取所有bit的时间待机功耗擦写、烧写功耗面积所需要的mask layer...
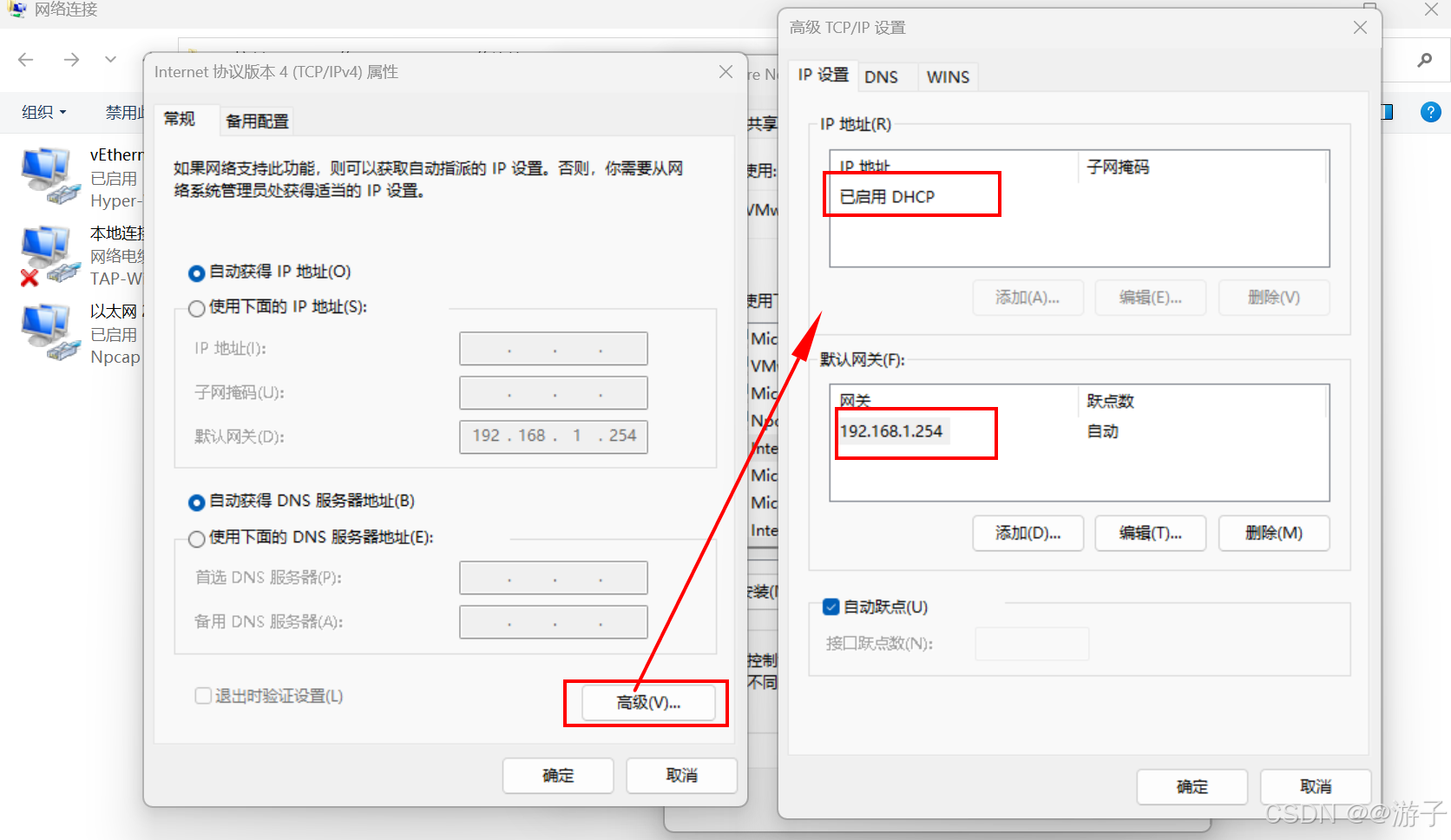
虚拟机网络不通的问题(这里以win10的问题为主,模式NAT)
当我们网关配置好了,DNS也配置好了,最后在虚拟机里还是无法访问百度的网址。 第一种情况: 我们先考虑一下,网关的IP是否和虚拟机编辑器里的IP一样不,如果不一样需要更改一下,因为我们访问百度需要从物理机…...

SOC-ESP32S3部分:30-I2S音频-麦克风扬声器驱动
飞书文档https://x509p6c8to.feishu.cn/wiki/SKZzwIRH3i7lsckUOlzcuJsdnVf I2S简介 I2S(Inter-Integrated Circuit Sound)是一种用于传输数字音频数据的通信协议,广泛应用于音频设备中。 ESP32-S3 包含 2 个 I2S 外设,通过配置…...

比较数据迁移后MySQL数据库和ClickHouse数据仓库中的表
设计一个MySQL数据库和Clickhouse数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

break 语句和 continue 语句
break语句和continue语句都具有跳转作用,可以让代码不按既有的顺序执行 break break语句用于跳出代码块或循环 1 2 3 4 5 6 for (var i 0; i < 5; i) { if (i 3){ break; } console.log(i); } continue continue语句用于立即终…...
