大学生活题解

样例输入:
3
.xA
...
Bx.
样例输出:
6
思路分析:
这道题只需要在正常的广搜模板上多维护一个— —方向,如果当前改变方向,就坐标不变,方向变,步数加一;否则坐标变,方向不变,步数加一。
#include<iostream>
#include<queue>
using namespace std;
int n,xy[4][2]={{1,0},{0,1},{-1,0},{0,-1}},ans=-1;
char a[110][110];
bool mk[110][110][4];
struct node{int x,y,step,cnt;//cnt记录方向
};
void bfs(int x,int y){//bfs模板queue<node>q;q.push((node){x,y,0,-1});//起点方向标记-1while(q.size()){node t=q.front();if(a[t.x][t.y]=='B'){//判断是否到终点ans=t.step;return;}q.pop();for(int i=0;i<4;i++){int xx=t.x+xy[i][0],yy=t.y+xy[i][1];//偏移量if(xx>=1&&xx<=n&&yy>=1&&yy<=n&&a[xx][yy]!='x'&&mk[xx][yy][i]==0){//判断越界等if(t.cnt==-1||t.cnt==i){//特判-1和方向不变mk[xx][yy][i]=1;q.push((node){xx,yy,t.step+1,i});}else{//方向改变q.push((node){t.x,t.y,t.step+1,i});}}}}
}
int main(){cin>>n;int x,y;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>a[i][j];if(a[i][j]=='A'){x=i,y=j;}}}bfs(x,y);cout<<ans;return 0;
}相关文章:

大学生活题解
样例输入: 3 .xA ... Bx.样例输出: 6思路分析: 这道题只需要在正常的广搜模板上多维护一个— —方向,如果当前改变方向,就坐标不变,方向变,步数加一;否则坐标变,方向不…...

flask的配置项
flask的配置项 为了使 Flask 应用程序正常运行,有多种配置选项需要考虑。下面是一些基本的 Flask 配置选项: DEBUG: 这个配置项决定 Flask 是否应该在调试模式下运行。如果这个值被设为 True,Flask 将会提供更详细的错误信息,并…...

暑假刷题第16天--7/28
143. 最大异或对 - AcWing题库(字典树) #include<iostream> using namespace std; const int N100005; int a[N]; int nex[10000007][2],cnt; void insert(int x){int p0;for(int i30;i>0;i--){int ux>>i&1;if(!nex[p][u])nex[p][u]…...

vue vite ts electron ipc arm64
初始化 npm init vue # 全选 yes npm i # 进入项目目录后使用 npm install electron electron-builder -D npm install commander -D # 额外组件增加文件 新建 plugins 文件夹 src/background.ts 属于主进程 ipcMain.on、ipcMain.handle 都用于主进程监听 ipc,…...

数据分析-关于指标和指标体系
一、电商指标体系 二、指标体系的作用 三、统计学中基本的分析手段...

Vue+ElementUI操作确认框及提示框的使用
在进行数据增删改查操作中为保证用户的使用体验,通常需要显示相关操作的确认信息以及操作结果的通知信息。文章以数据的下载和删除提示为例进行了简要实现,点击下载以及删除按钮,会出现对相关信息的提示,操作结果如下所示。 点击…...

宋浩线性代数笔记(二)矩阵及其性质
更新线性代数第二章——矩阵,本章为线代学科最核心的一章,知识点多而杂碎,务必仔细学习。 重难点在于: 1.矩阵的乘法运算 2.逆矩阵、伴随矩阵的求解 3.矩阵的初等变换 4.矩阵的秩 (去年写的字,属实有点ugl…...

Linux之Shell 编程详解(二)
第 9 章 正则表达式入门 正则表达式使用单个字符串来描述、匹配一系列符合某个语法规则的字符串。在很多文 本编辑器里,正则表达式通常被用来检索、替换那些符合某个模式的文本。在 Linux 中,grep, sed,awk 等文本处理工具都支持…...
TCP网络通信编程之字节流
目录 【TCP字节流编程】 // 网络编程中,一定是server端先运行 【案例1】 【思路分析】 【客户端代码】 【服务端代码】 【结果展示】 【案例2】 【题目描述】 【注意事项】 【服务端代码】 【客户端代码】 【代码结果】 【TCP字节流编程】 // 网络编程中&a…...

【暑期每日一练】 day8
目录 选择题 (1) 解析: (2) 解析: (3) 解析: (4) 解析: (5) 解析: 编程题 题一 描述…...

maven的基本学习
maven https://www.bilibili.com/video/BV14j411S76G?p1&vd_source5c648979fd92a0f7ba8de0cde4f02a6e 1.简介 1.1介绍 Maven翻译为"专家"、“内行”,是Apache下的一个纯Java开发的开源项目。基于项目对象模型(缩写:POM)概念,Maven利用一…...

疲劳驾驶检测和识别2:Pytorch实现疲劳驾驶检测和识别(含疲劳驾驶数据集和训练代码)
疲劳驾驶检测和识别2:Pytorch实现疲劳驾驶检测和识别(含疲劳驾驶数据集和训练代码) 目录 疲劳驾驶检测和识别2:Pytorch实现疲劳驾驶检测和识别(含疲劳驾驶数据集和训练代码) 1.疲劳驾驶检测和识别方法 2.疲劳驾驶数据集 (1)疲…...
安防监控视频汇聚EasyCVR修改录像计划等待时间较长,是什么原因?
安防监控视频EasyCVR视频融合汇聚平台基于云边端智能协同,支持海量视频的轻量化接入与汇聚、转码与处理、全网智能分发等。音视频流媒体视频平台EasyCVR拓展性强,视频能力丰富,具体可实现视频监控直播、视频轮播、视频录像、云存储、回放与检…...

EXCEL数据自动web网页查询----高效工作,做个监工
目的 自动将excel将数据填充到web网页,将反馈的数据粘贴到excel表 准备 24KB的鼠标连点器软件(文末附链接)、Excel 宏模块 优势 不需要编程、web验证、爬虫等风险提示。轻量、稳定、安全。 缺点 效率没那么快 演示 宏环境 ht…...

visual studio 2022换背景遇到的问题
如果要自定义背景图,则可以下载ClaudialIDE 1.在拓展->点击拓展管理->右上角搜索background->点击下载ClaudialIDE->加载完之后需要关闭vs界面进行下载,下载失败,弹出“由于出现以下错误 无法安装一个或多个扩展”。 解决&#x…...
MODBUS-TCP转Ethernet IP 网关连接空压机 配置案例
本案例是工业现场应用捷米特JM-EIP-TCP的Ethernet/IP转Modbus-TCP网关连接欧姆龙PLC与空压机的配置案例。使用设备:欧姆龙PLC,捷米特JM-EIP-TCP网关, ETHERNET/IP 的电气连接 ETHERNET/IP 采用标准的 T568B 接法,支持直连和交叉接…...

Go重写Redis中间件 - GO实现TCP服务器
GO实现TCP服务器 首先新建一个项目go-redis,将config和lib包放到项目中,config.go用来解析配置,比如端口、功能、DB数;lib包有两个文件夹,分别是logger和sync,其中logger.go是一个日志框架,sync包中的bool.go包装了atomic操作,因为atomic原生没有bool类型,所以将uint…...
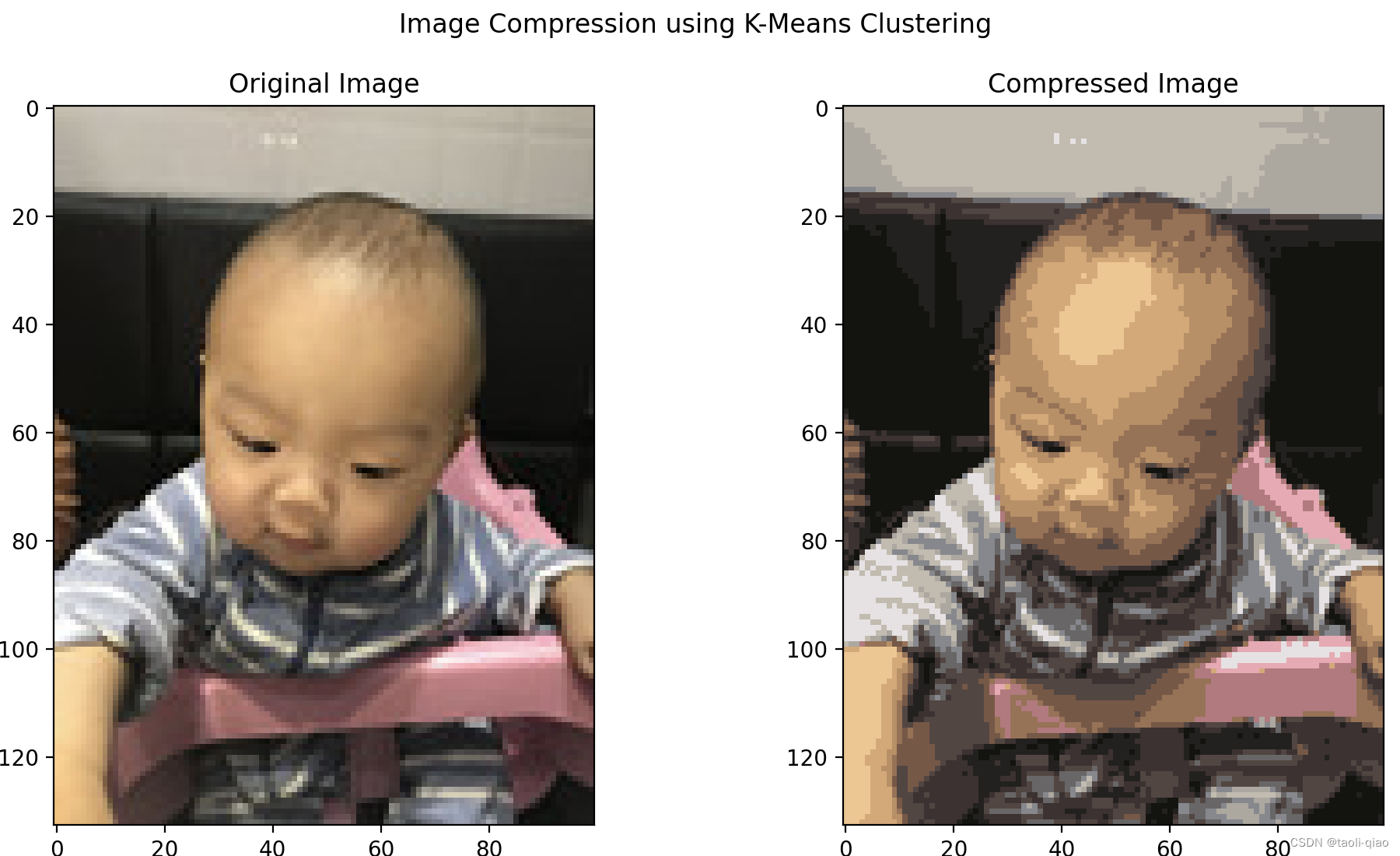
使用Kmeans算法完成聚类任务
聚类任务 聚类任务是一种无监督学习任务,其目的是将一组数据点划分成若干个类别或簇,使得同一个簇内的数据点之间的相似度尽可能高,而不同簇之间的相似度尽可能低。聚类算法可以帮助我们发现数据中的内在结构和模式,发现异常点和离…...
内网穿透技术 - 带你玩转NATAPP
前言 使用内网穿透工具,我们就可以在公网中直接访问在局域网内搭建的服务器网页,也可以直接远程连接到局域网内的机器。本文章主要介绍下NATAPP内网穿透工具的使用。 NATAPP使用教程 官网 在官网先注册,然后登录。登录后,会有一…...

SQL server 简介
SQL server 简介 学习目的 SQL Server 是由微软公司开发的一种关系型数据库管理系统(RDBMS),用于存储和检索数据。它提供了一个可扩展的、安全的和可靠的数据存储和管理解决方案。 SQL Server 主要用于构建企业级应用程序,支持…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...

boost::filesystem::path文件路径使用详解和示例
boost::filesystem::path 是 Boost 库中用于跨平台操作文件路径的类,封装了路径的拼接、分割、提取、判断等常用功能。下面是对它的使用详解,包括常用接口与完整示例。 1. 引入头文件与命名空间 #include <boost/filesystem.hpp> namespace fs b…...
