数值分析第六章节 用Python实现解线性方程组的迭代法
参考书籍:数值分析 第五版 李庆杨 王能超 易大义编 第5章 解线性方程组的迭代法
文章声明:如有发现错误,欢迎批评指正
文章目录
- 迭代法的基本概念
- 雅可比迭代法与高斯-塞格尔迭代法
- 雅可比迭代法
- 高斯-塞格尔迭代法
迭代法的基本概念
6.1.1引言:定义:(1)对于给定的线性方程组 x = B x + f x=Bx+f x=Bx+f,用公式 x ( k + 1 ) = B x ( k ) + f x^{(k+1)}=Bx^{(k)}+f x(k+1)=Bx(k)+f逐步带入求近似解的方法称为迭代法(或称为一阶定常迭代法,这里 B B B与 k k k无关)(2)如果 lim k → ∞ x ( k ) \lim\limits_{k\rightarrow\infty}x^{(k)} k→∞limx(k)存在(记为 x ∗ x^* x∗),称此迭代法收敛,显然 x ∗ x^{*} x∗就是此方程组的解,否则称此迭代法发散。6.1.2:向量序列与矩阵序列的极限:给定线性方程组 x = B x + f x=Bx+f x=Bx+f及一阶定常迭代法 x ( k + 1 ) = B x ( k ) + f x^{(k+1)}=Bx^{(k)}+f x(k+1)=Bx(k)+f式,对任意选取初始向量 x ( 0 ) x^{(0)} x(0),迭代法 x ( k + 1 ) = B x ( k ) + f x^{(k+1)}=Bx^{(k)}+f x(k+1)=Bx(k)+f式收敛的充要条件是矩阵 B B B的谱半径 ρ ( B ) < 1 \rho(B)<1 ρ(B)<1。其他跳过。
雅可比迭代法与高斯-塞格尔迭代法
雅可比迭代法
{ x ( 0 ) x ( k + 1 ) = B x ( k ) + f , k = 0 , 1 , … , x ( 0 ) 为初始向量, B = D − 1 ( L + U ) , f = D − 1 b \left\{\begin{matrix}x^{(0)}\\x^{(k+1)}=Bx^{(k)}+f,k=0,1,\dots,\end{matrix}\right.x^{(0)}为初始向量,B=D^{-1}(L+U),f=D^{-1}b {x(0)x(k+1)=Bx(k)+f,k=0,1,…,x(0)为初始向量,B=D−1(L+U),f=D−1b
我感觉我写得挺好,可以算作通用代码,前提必须保证收敛。输入:输入系数矩阵行数,系数矩阵,初始向量,迭代次数。输出:解的向量。命名十分规范,懂了理论不难看懂。
def func1(B,x):#不通用的矩阵乘法global nlt=[]for i in range(n):cnt=0for j in range(n):cnt+=B[i][j]*x[j]lt.append(cnt)return lt
def func2(Bx,f):#不通用的矩阵加法global nlt=[]for i in range(n):lt.append(Bx[i]+f[i])return lt
n=int(input())
lt=[]
for _ in range(n):lt.append([eval(_) for _ in input().strip().split()])
D_inv=[[0 for _ in range(n)] for _ in range(n)]
for i in range(n):D_inv[i][i]=1/lt[i][i]
L_sum_U=[[0 for _ in range(n)] for _ in range(n)]
for i in range(1,n):for j in range(i):L_sum_U[i][j]=-lt[i][j]
for i in range(n-1):for j in range(i+1,n):L_sum_U[i][j]=-lt[i][j]
B=[[0 for _ in range(n)] for _ in range(n)]
for i in range(n):for j in range(n):B[i][j]=L_sum_U[i][j]*D_inv[i][i]
f=[0 for _ in range(n)]
for i in range(n):f[i]=D_inv[i][i]*lt[i][-1]
x=[eval(_) for _ in input().strip().split()]
num=int(input())
for _ in range(1,num+1):x=func2(func1(B,x),f)
print(x)
用的例1,一模一样。

高斯-塞格尔迭代法
{ x ( 0 ) x ( k + 1 ) = B x ( k ) + f , k = 0 , 1 , … , x ( 0 ) 为初始向量, B = ( D − L ) − 1 U , f = ( D − L ) − 1 b \left\{\begin{matrix}x^{(0)}\\x^{(k+1)}=Bx^{(k)}+f,k=0,1,\dots,\end{matrix}\right.x^{(0)}为初始向量,B=(D-L)^{-1}U,f=(D-L)^{-1}b {x(0)x(k+1)=Bx(k)+f,k=0,1,…,x(0)为初始向量,B=(D−L)−1U,f=(D−L)−1b
我感觉我写得挺好,可以算作通用代码,前提必须保证收敛。输入:输入系数矩阵行数,系数矩阵,初始向量,迭代次数。输出:解的向量。命名十分规范,懂了理论不难看懂。
def func1(lt1,lt2):#矩阵乘法a,b=len(lt1),len(lt2[0])lt=[[0 for _ in range(b)] for _ in range(a)]for i in range(a):for j in range(b):for p in range(len(lt1[0])):lt[i][j]+=lt1[i][p]*lt2[p][j]return lt
def func2(lt1,lt2):#不通用的矩阵加法global nlt=[]for i in range(n):lt.append([lt1[i][0]+lt2[i][0]])return lt
n=int(input())
lt=[]
for _ in range(n):lt.append([eval(_) for _ in input().strip().split()])
D=[[0 for _ in range(n)] for _ in range(n)]
for i in range(n):D[i][i]=lt[i][i]
L=[[0 for _ in range(n)] for _ in range(n)]
for i in range(1,n):for j in range(i):L[i][j]=-lt[i][j]
U=[[0 for _ in range(n)] for _ in range(n)]
for i in range(n-1):for j in range(i+1,n):U[i][j]=-lt[i][j]
D_minus_L=[[0 for _ in range(n)] for _ in range(n)]
for i in range(n):for j in range(n):D_minus_L[i][j]=D[i][j]-L[i][j]
#这里涉及一个求解下三角阵的逆矩阵
D_minus_L_inv=[[0 for _ in range(n)] for _ in range(n)]
for i in range(n):for j in range(i):cnt=0for k in range(i):cnt-=D_minus_L[i][k]*D_minus_L_inv[k][j]D_minus_L_inv[i][j]=cnt/D_minus_L[i][i]D_minus_L_inv[i][i]=1/D_minus_L[i][i]
B=func1(D_minus_L_inv,U)
f=func1(D_minus_L_inv,[[lt[_][-1]] for _ in range(n)])
x=[[eval(_)] for _ in input().strip().split()]
num=int(input())
for _ in range(1,num+1):x=func2(func1(B,x),f)
print(x)
用的例1,一模一样。

就这样吧,剩下方法,自己研究。
相关文章:

数值分析第六章节 用Python实现解线性方程组的迭代法
参考书籍:数值分析 第五版 李庆杨 王能超 易大义编 第5章 解线性方程组的迭代法 文章声明:如有发现错误,欢迎批评指正 文章目录 迭代法的基本概念雅可比迭代法与高斯-塞格尔迭代法雅可比迭代法高斯-塞格尔迭代法 迭代法的基本概念 6.1.1引言…...

【低代码专题方案】使用iPaaS平台下发数据,快捷集成MDM类型系统
01 场景背景 伴随着企业信息化建设日趋完善化、体系化,使用的应用系统越来越多,业务发展中沉淀了大量数据。主数据作为数据治理中枢,保存大量标准数据库,如何把庞大的数据下发到各个业务系统成了很棘手的问题。 传统的数据下发方…...
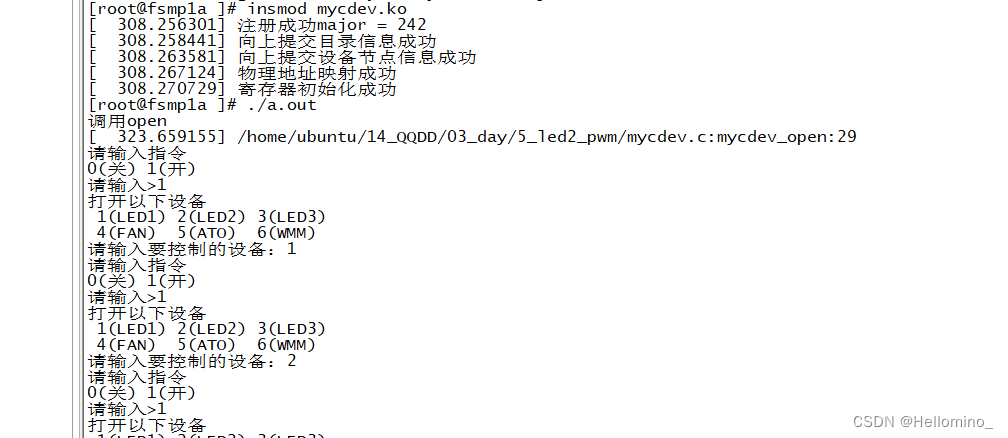
驱动开发 day3 (模块化驱动启动led,蜂鸣器,风扇,震动马达)
模块化驱动启动led,蜂鸣器,风扇,震动马达并加上Makefile 封装模块化驱动,可自由安装卸载驱动,便于驱动更新(附图) 1.安装模块驱动同时初始化各个设备并使能 2.该驱动会自动创建驱动节点. 3.通过c函数程序输入控制各个设备 4.卸载模块驱动 //编译驱动…...
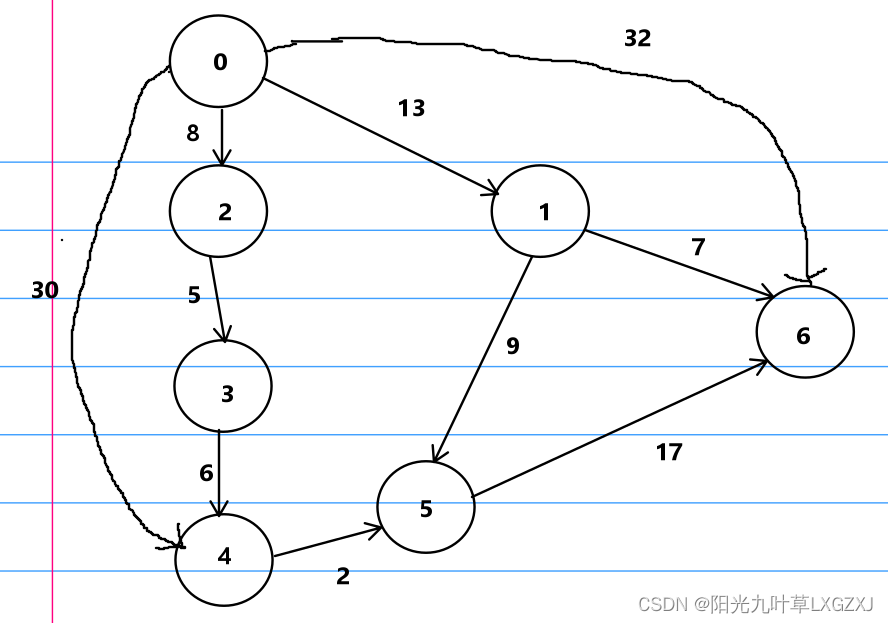
数据结构与算法基础-学习-27-图之最短路径之Dijkstra(迪杰斯特拉)算法
一、最短路径应用案例 例如从北京到上海旅游,有多条路可以到目的地,哪条路线最短,哪条路线最省钱,就是典型的最短路径问题。 二、最短路径问题分类 最短路径问题可以分为两类,第一类为:两点间最短路径。第…...
Windows Server 2012 能使用的playwright版本
由于在harkua_bot里面使用到了playwright,我的服务器又是Windows Server 2012 R2,最新版playwright不支持Windows Server 2012 R2,支持Windows Server 2016以上,所以有了这个需求 https://cdn.npmmirror.com/binaries/playwright…...

css实现溢出变为省略号
单行文本溢出省略 text-overflow:规定当文本溢出时,显示省略符号来代表被修剪的文本 white-space:设置文字在一行显示,不能换行 overflow:文字长度超出限定宽度,则隐藏超出的内容overflow设为hidden&#…...

nginx如何配置两个服务器的连接
nginx 中通过server_name listen的方式配置多个服务器 nginx配置两个站点的windows操作方法,双域名双站点...

Linux环境Arduino IDE中配置ATOM S3
linux选择ubuntu发行版。 硬件设备有多小呢: 功能超级强大。 之前的ROS1和ROS2案例已经全部移植完成并测试结束(三轮纯人力校验😎)。 官网文档信息非常非常好: https://docs.m5stack.com/zh_CN/quick_start/atoms3…...
【C#】.Net Framework框架下的Authorize权限类
2023年,第31周,第3篇文章。给自己一个目标,然后坚持总会有收货,不信你试试! 在C#的.NET Framework中,你可以使用Authorize类来处理权限认证。Authorize类位于System.Web.Mvc命名空间中,它提供了…...

C++ list底层实现原理
文章目录 一、list底层实现二、类构成三、构造函数四、迭代器五、获取第一个元素六、获取最后一个元素七、插入元素 一句话:list底层实现一个双向循环链表 一、list底层实现 一个双向循环链表 二、类构成 class list : protected_List_base_list_base.lsit_impl…...

C#实现数字验证码
开发环境:VS2019,.NET Core 3.1,ASP.NET Core API 1、建立一个验证码控制器 新建两个方法Create和Check,Create用于创建验证码,Check用于验证它是否有效。 声明一个静态类变量存放列表,列表中存放包含令…...

Git的常用命令以及使用场景
文章目录 1.前言2.工作区,暂存区,版本库简介3.Git的常用命令4.版本回退5.撤销修改6.删除文件7.总结 1.前言 在学习Git命令之前,需要先了解工作区,暂存区和版本库这三个概念 2.工作区,暂存区,版本库简介 在使用Git进行版本控制时,有三个重要的概念:工作…...

tcp keepalive
tcp keepalive用于检查两者之间的链路是否正常,或防止链路断开。 一旦建立了TCP连接,该连接被定义为有效,直到一方关闭它。一旦连接进入连接状态,它将无限期地保持连接状态。但实际上,这种联系不会无限期地持续下去。如…...

PP-Matting: AI高精度图像前景Matting,让抠图轻而易举
分割和Matting的一个重要区别是:分割返回的是像素分类标签,其结果是整型数据;而Matting返回的是属于前景或背景的概率P,从而在前景与背景交互区域产生渐变的效果,使得抠图更加自然。Matting分割模型训练完成后,对于原始图像每个位置上的像素,都将生成一个表示其前景透明…...
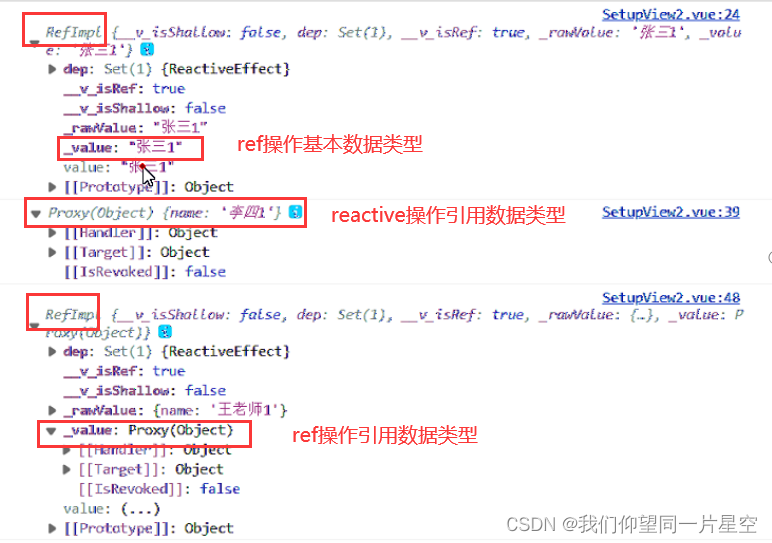
VUE3-01
1.选项式和组合式 选项式API:按照作用组织代码 组合式API:按照功能组织代码 2.<script setup> <template><div class"about"><h1>{{name}}</h1><button click"sayHello">测试</button>…...
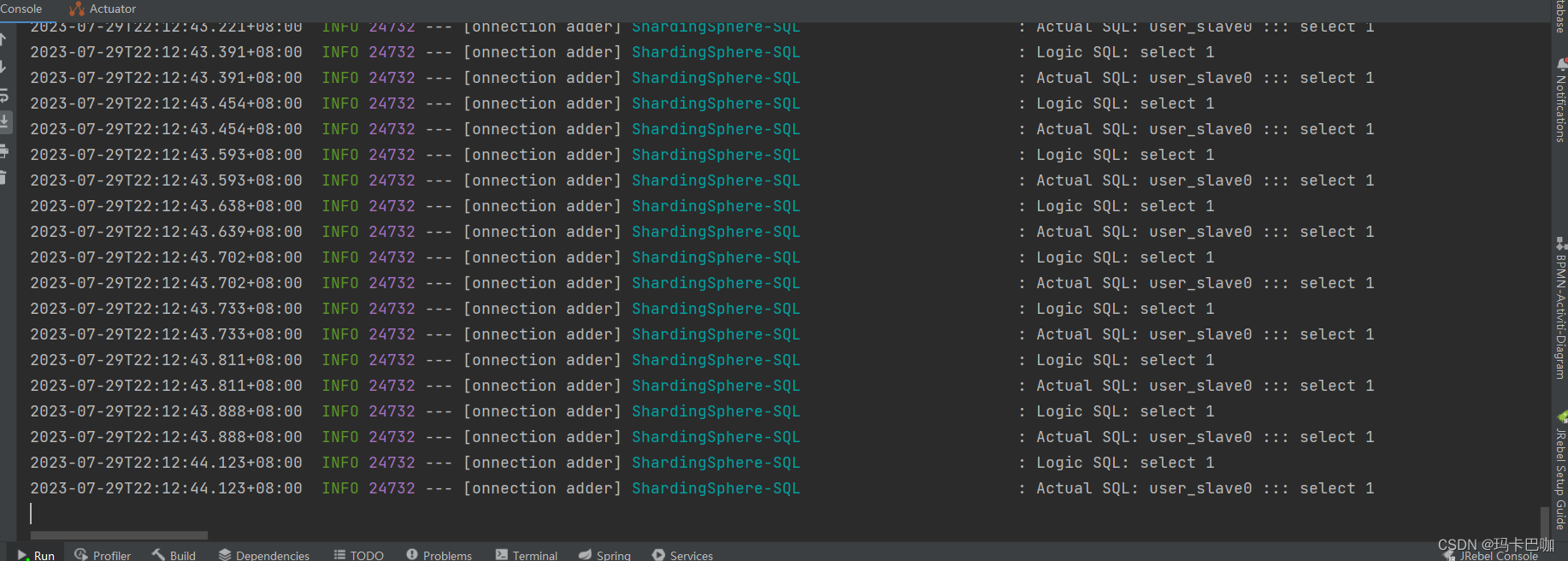
分库分表之基于Shardingjdbc+docker+mysql主从架构实现读写分离(二)
说明:如果实现了docker部署mysql并完成主从复制的话再继续,本篇文章主要说明springboot配置实现Shardingjdbc进行读写分离操作。 如果没实现docker部署mysql实现主从架构的话点击我 Shardingjdbc配置介绍(版本:5.3.2)…...

Python 进阶(四):日期和时间(time、datetime、calendar 模块)
❤️ 博客主页:水滴技术 🌸 订阅专栏:Python 入门核心技术 🚀 支持水滴:点赞👍 收藏⭐ 留言💬 文章目录 1. time模块1.1 获取当前时间1.2 时间休眠1.3 格式化时间 2. datetime模块2.1 获取当前…...
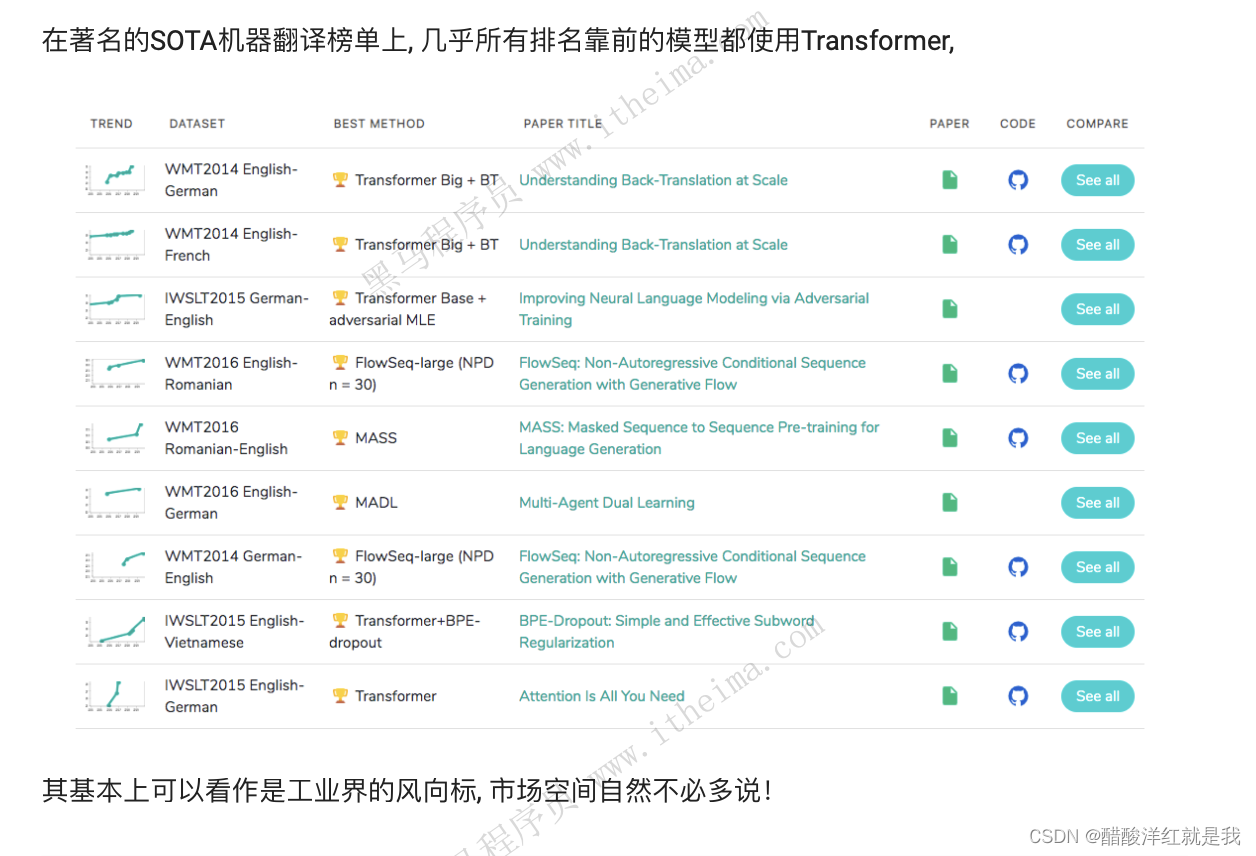
Transformer背景介绍
目录 Transformer的诞生Transformer的优势Transformer的市场 Transformer的诞生 论文地址 Transformer的优势 Transformer的市场...

深入理解BeanDefinition和Spring Beans
深入理解BeanDefinition和Spring Beans 引言 在Spring框架中,BeanDefinition和Spring Beans是非常重要的概念。BeanDefinition定义了Spring Bean的元数据,而Spring Beans是应用程序中的对象实例。理解BeanDefinition和Spring Beans的概念和使用方法对于…...
实验六 调度器-实验部分
目录 一、知识点 1.进程调度器设计的目标 1.1.进程的生命周期 1.2.用户进程创建与内核进程创建 1.3.进程调度器的设计目标 2.ucore 调度器框架 2.1.调度初始化 2.2.调度过程 2.2.1.调度整体流程 2.2.2.设计考虑要点 2.2.3.数据结构 2.2.4.调度框架应与调度算法无关…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
