教雅川学缠论04-笔
笔由3部分组成:
顶分型+K线+底分型,或者
底分型+K线+顶分型
注意:笔加一起至少7根K线,因为一个底分型至少3根,K先至少1个,顶分型至少3根
下图中红色线段就是一个标准的笔,它始于一个底分型,途径一根K线,终止与一个顶分型
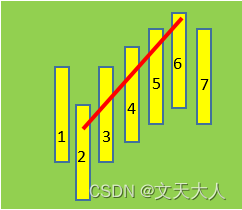
下图中就不是笔,因为它不满足7根K线
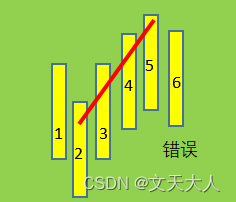
现在理解了笔的概念,我们使用2023年4-7月的武汉控股K线,画一下,注意两个蓝色虚线方框中的部分,这部分为什么没有笔?因为该两部分虽然是底分型+顶分型,但是不足7根K线,所以原笔继续前进
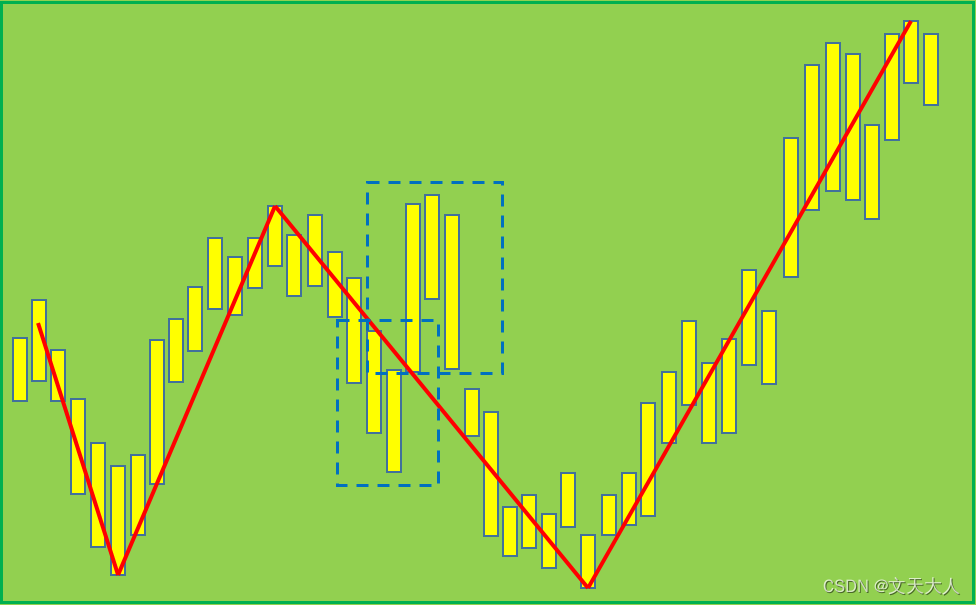
到此为止,笔的概念就已经介绍完毕
相关文章:

教雅川学缠论04-笔
笔由3部分组成: 顶分型K线底分型,或者 底分型K线顶分型 注意:笔加一起至少7根K线,因为一个底分型至少3根,K先至少1个,顶分型至少3根 下图中红色线段就是一个标准的笔,它始于一个底分型ÿ…...
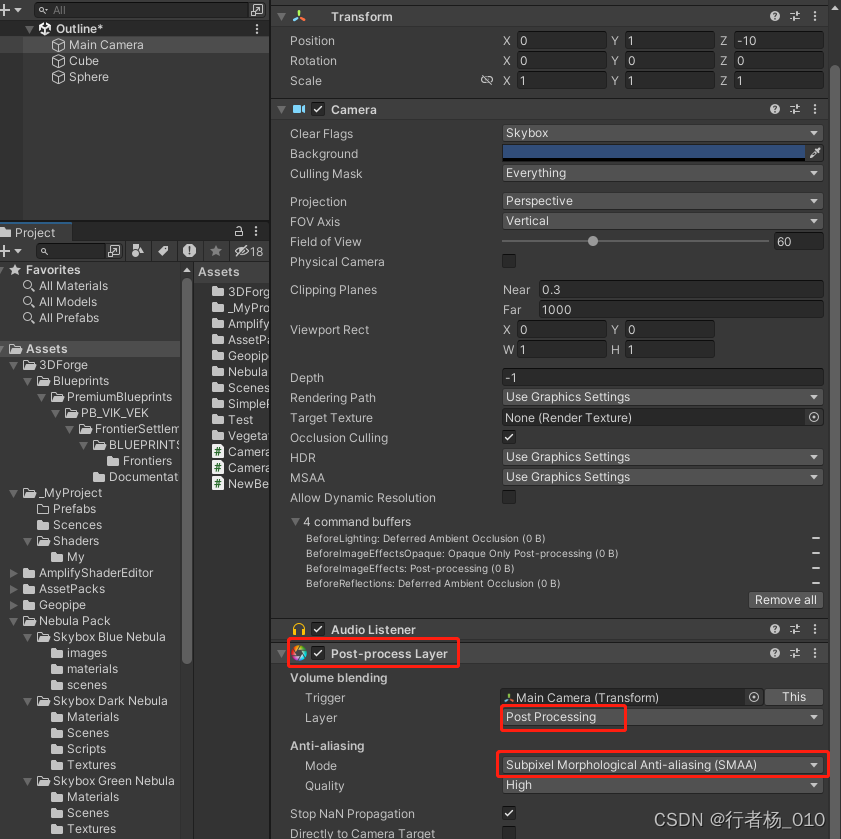
Unity3d_post process layer 抗锯齿设置
1、 2、 3、 4、 5、...
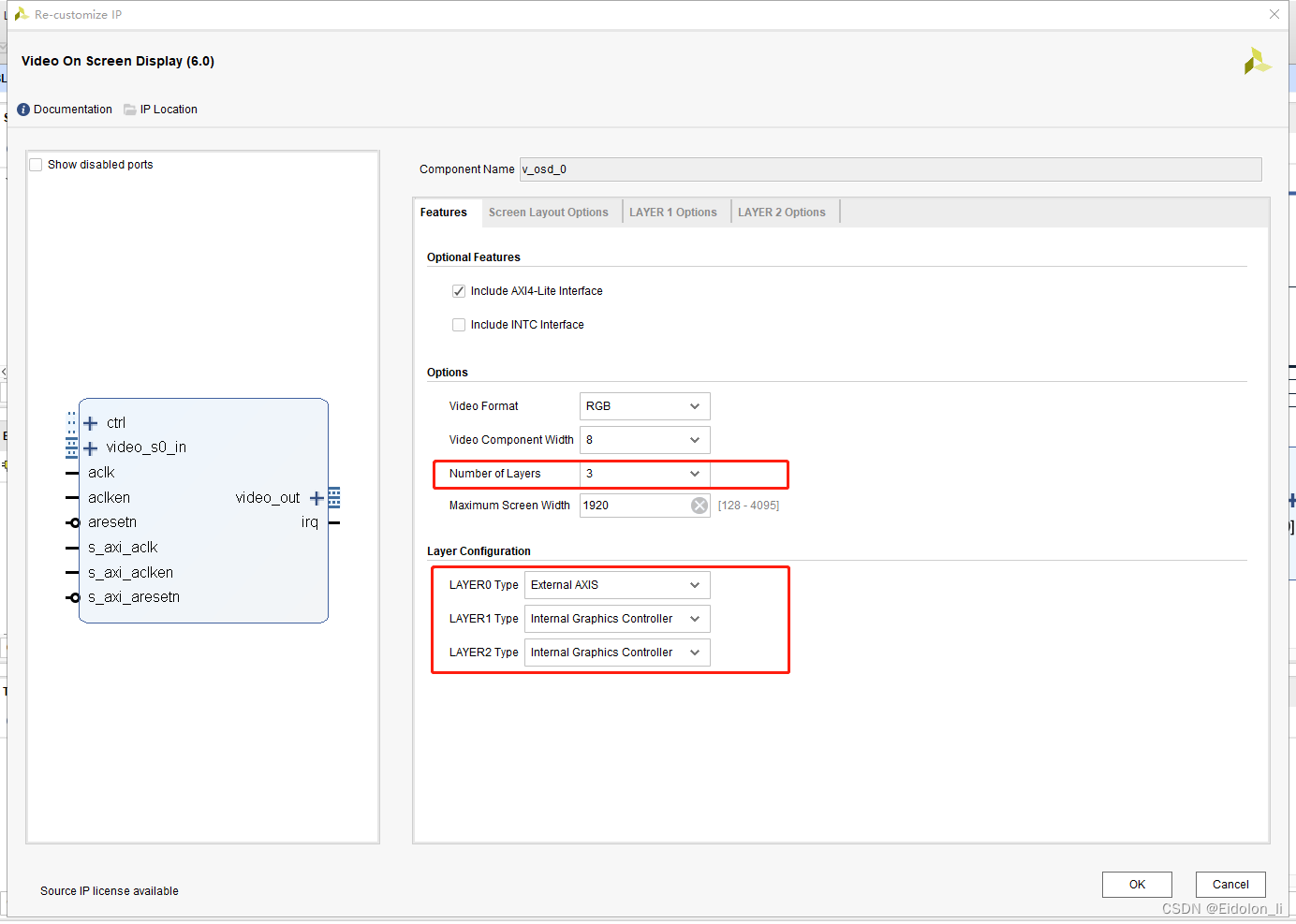
基于FPGA实现OSD功能
简介 基于FPGA平台实现简单的OSD的功能,对于FPGA实现OSD只能实行简单的画框和文字叠加,如果实现复杂的车道线画框,则没法实现(起码我个人感觉,这个功能没有思路执行)。 FPGA实现OSD功能需要7系列平台,以及VDMA、OSD等Xilinx公司的IP使用(本功能工程采用Vivado2017.4平台…...

Java019-1——面向对象的三大特性
一、封装性 将类的某些信息隐藏在类内部,不允许外部程序直接访问,而是通过该类提供的方法来实现对隐藏信息的操作和访问。(这里说的信息就是类中的属性和方法) 1.1、封装性的体现 想要通过代码体现封装性之前,需要先…...
2023年的深度学习入门指南(22) - 百川大模型13B的运行及量化
2023年的深度学习入门指南(22) - 百川大模型13B的运行及量化 不知道上一讲的大段代码大家看晕了没有。但是如果你仔细看了会发现,其实代码还是不全的。比如分词器我们就没讲。 另外,13B比7B的改进点也没有讲。 再有,对于13B需要多少显存我们…...
方法函数)
无涯教程-jQuery - empty( )方法函数
empty()方法删除所有匹配的子节点。 empty( ) - 语法 selector.empty( ) empty( ) - 示例 以下是一个简单的示例,简单说明了此方法的用法- <html><head><title>The jQuery Example</title><script type"text/javascript"…...

微信小程序实现蓝牙开锁、开门、开关、指令发送成功,但蓝牙设备毫无反应、坑
文章目录 开源htmlJavaScript 开源 wx联系本人获取源码(开源): MJ682517 html <view><view class"p_l_36 p_r_36"><input class"w_100_ h_80 lh_80 ta_c b_2s_eee radius_20" value"{{instructVal}}" type"text" plac…...

微信小程序中使用echarts方法
小程序中使用echarts echarts是一个基于JS的数据可视化图标库,它提供了直观,生动,可交互,可个性定制的数据可视化图表。一般在vue中会使用到,并且官网也详细的说明了如何在vue中使用,但是今天我想来探讨的…...

【面试题】前端中 JS 发起的请求可以暂停吗?
这个问题非常有意思,我一看到就想了很多可以回复的答案,但是评论区太窄,就直接开一篇文章来写了。 审题 JS 发起的请求可以暂停吗?这一句话当中有两个概念需要明确,一是什么样的状态才能称之为 暂停?二是…...
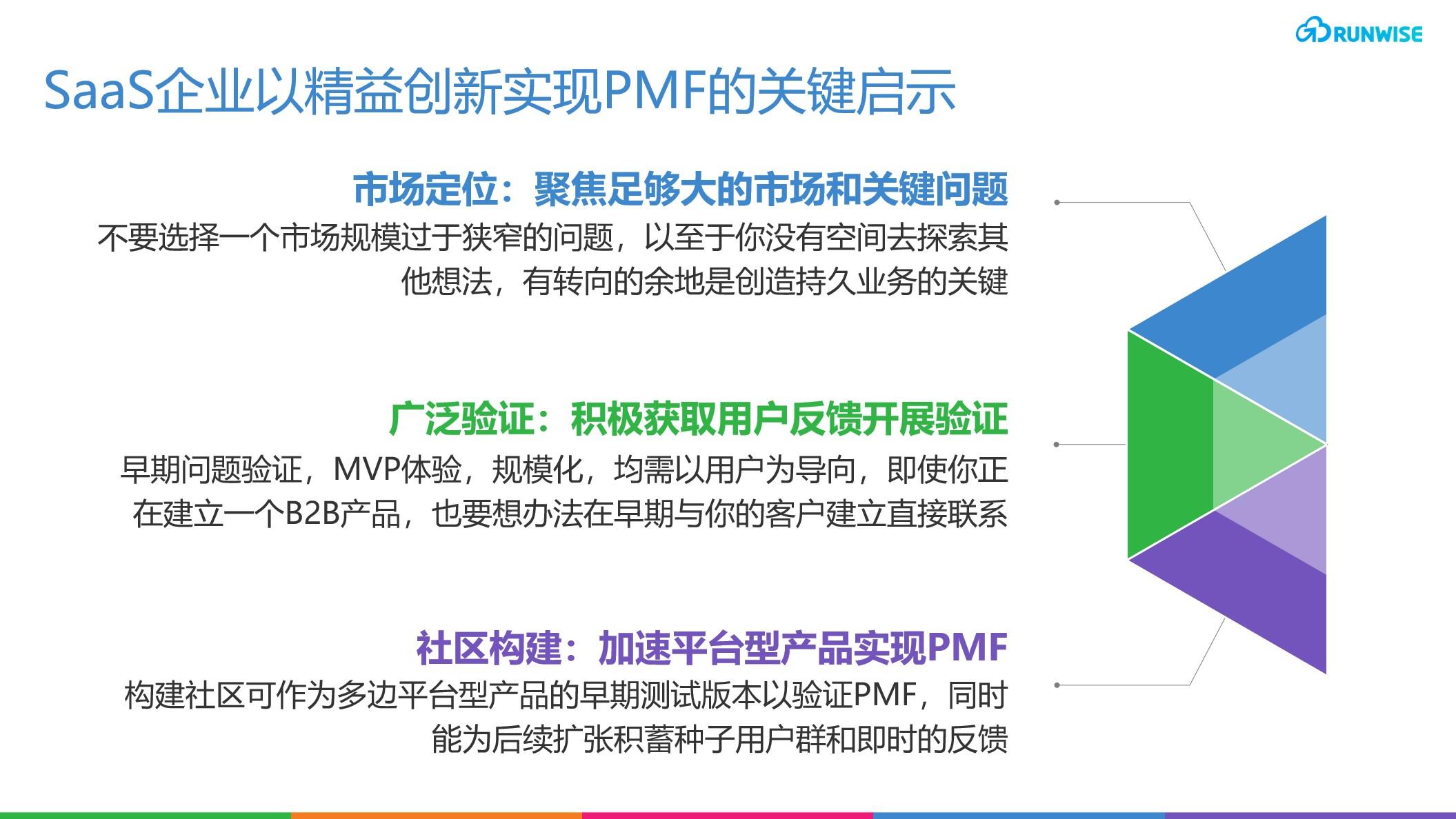
通过社区参与解锁早期增长:Maven 远程医疗平台概览
Maven通过用户导向的渐进式验证,找到了一个被忽视的巨大女性医疗服务市场,作为女性医疗保健的先行者,已服务超过1500万用户,目前估值已达$14亿。本文将深入探索Maven实现产品市场匹配的三个阶段,从如何验证初始的市场机…...
Vue中使用echarts
1 安装 npm install -g cnpm --registryhttps://registry.npm.taobao.org cnpm install echarts -S 2 main.js引入 3 引入成功...
边缘计算对现代交通的重要作用
边缘计算之所以重要,是在于即使在5G真正商用之时,可以实现超大带宽(eMBB)的应用场景,但庞大数据量的涌现也就意味着需要在云和端传输过程中找到一个承接点,对数据进行预处理再选择是否上云。 边缘计算应用演…...

Python桥接模式介绍、使用
一、Python桥接模式介绍 概念: Python桥接模式(Bridge Pattern)是一种软件设计模式,用于将抽象部分与其实现部分分离,使它们可以独立地变化。 它可以通过使用桥接接口来创建一个桥接对象来连接抽象和实现部分。 功能…...

ChatGPT在知识图谱的构建和更新中的应用如何?
ChatGPT在知识图谱的构建和更新中具有重要的应用潜力。知识图谱是一种用于表示和存储结构化知识的图形化数据模型,通常由实体、属性和关系组成。知识图谱的构建和更新是一个复杂而关键的过程,涉及知识的收集、组织、链接和推理。ChatGPT作为一种预训练语…...
JS正则表达式:常用正则手册/RegExp/正则积累
一、正则基础语法 JavaScript 正则表达式 | 菜鸟教程 JS正则表达式语法大全(非常详细) 二、使用场景 2.1、校验中国大陆手机号的正则表达式 正则 /^1[3456789]\d{9}$/解释 序号正则解释1^1以数字 1 开头2[3456789]第二位可以是 3、4、5、6、7、8、…...

自动化测试框架unittest与pytest的区别!
引言 前面文章已经介绍了python单元测试框架,大家平时经常使用的是unittest,因为它比较基础,并且可以进行二次开发,如果你的开发水平很高,集成开发自动化测试平台也是可以的。而这篇文章主要讲unittest与pytest的区别&…...
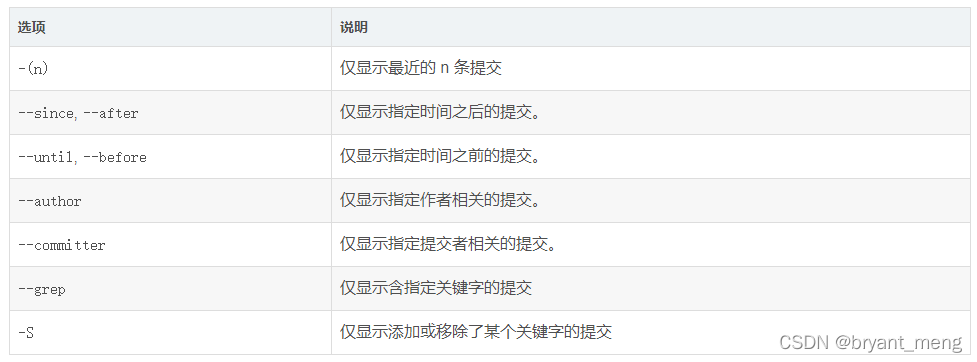
【Git】
学习来自于: 女朋友乱用Git,差点把我代码删了。。。 一些常用的Git 知识点整理 关于Git这一篇就够了 Git基本命令大全 30分钟精通Git,学不会来找我 Git 版本管理 | 莫烦PYTHON Git 代码版本管理教程 文章目录 【前言】集中式与分布式的…...

[论文笔记] CLRerNet: Improving Confidence of Lane Detection with LaneIoU
Honda, Hiroto, and Yusuke Uchida. “CLRerNet: Improving Confidence of Lane Detection with LaneIoU.” arXiv preprint arXiv:2305.08366 (2023). 2023.05 出的一篇车道线检测的文章, 效果在CULane, CurveLanes SOTA 文章目录 简介LaneIoULineIoU存在问题为什么使用LaneIo…...

LeetCode|backtracking|review:40. 131. 93. 47. 332. | 37. Sudoku Solver
复习: 40. Combination Sum II [1,1,2,3]中,答案里有[1,1,2], 但是不能有两个[1,2,3] 131. Palindrome Partitioning 每个for都是在给定的start之后找一个palindrome。当start 93. Restore IP Addresses forloop每次loop都是在给定的start的后三个数…...

被泼冷水后,谁能超越微服务?
历史总会重演。一切刚过去的,又会被重新提起。开源项目Codename One的联合创始人Shai,曾是Sun Microsystems开源LWUIT项目的共同作者,参与了无数开源项目。作为最早一批Java开发者,最近感慨道:单体,又回来了…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...
