电磁波定义、特性以及信道相关知识
文章目录
- 前言
- 一、电磁波的定义、特性、波谱
- 1、电磁波的特性
- 2、电磁波谱的划分及用途
- 二、地球大气层的结构
- 三、电磁波的传播方式
- 1、地波(ground-wave)
- 2、天波(sky-wave)
- 3、视线传播(line-of-sight)
- ①、相关特性
- ②、增大视线传播距离的其他途径
- 四、随参信道的特性与影响
- 1、随参信道的特性
- 2、多径传播对于宽带信号的影响
- ①、频率选择性衰落
- ②、避免频率选择性衰落的方法
- 3、OFDM —— 减小频率选择性衰落的有效措施之一
- ①、定义
- ②、思想
- 五、信道容量
- 1、无扰信道的容量——奈奎斯特定理
- 2、有扰信道的容量——香农公式
- ①、定义
- ②、结论
- ③、应用
- 3、联系
前言
记录一下通信原理学习笔记,主要内容包括电磁波的概念及传播方式,以及随参信道的特性与影响、信道容量相关知识。
一、电磁波的定义、特性、波谱
1、电磁波的特性
- 低频电磁波,主要束缚在有形的导电体内传递。
- 高频电磁波,即可在空间,也可在导电体内传递。
- 电磁波在空间的传播速度等于光速: c = 3 c=3 c=3x 1 0 8 m / s 10^8m/s 108m/s
- 频率 f f f和波长 λ \lambda λ是电磁波的重要特性: λ = c f \lambda=\large \frac{c}{f} λ=fc
- 为了有效地发射和接收电磁波,天线尺寸: h ≥ λ 10 h\geq\large \frac{\lambda}{10} h≥10λ
=======> f f f越高 --> λ \lambda λ越短 --> h h h越小
2、电磁波谱的划分及用途
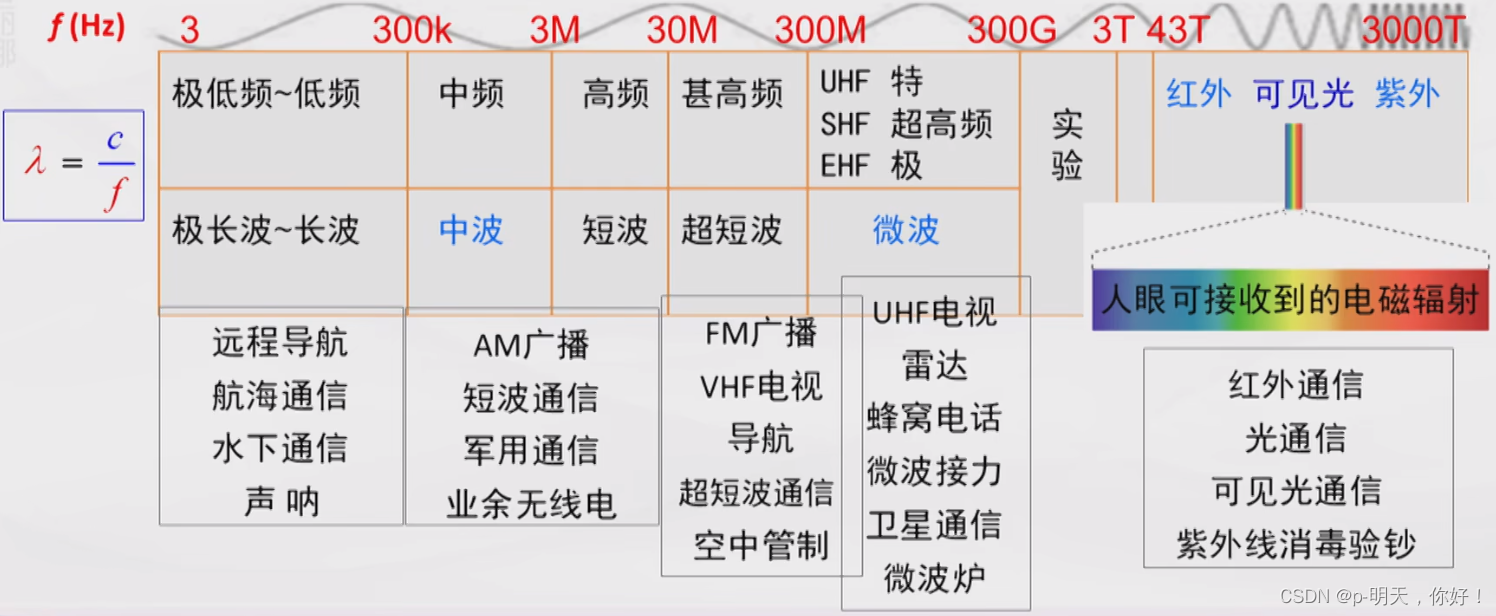
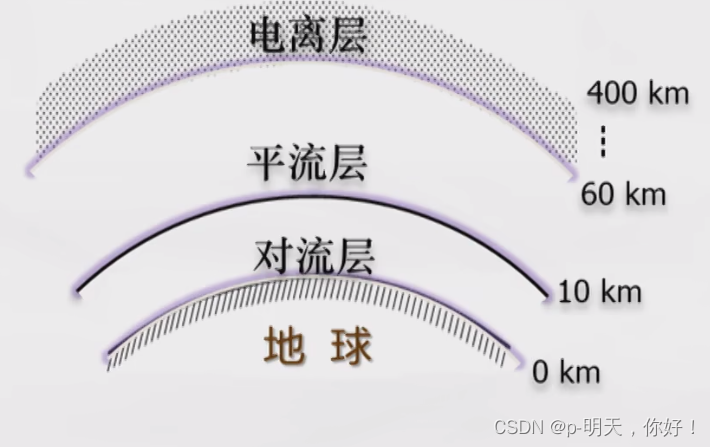
二、地球大气层的结构
- 对流层:约 0~10 km
- 平流层:约 10~60 km
- 电离层:约 60~400 km
三、电磁波的传播方式
1、地波(ground-wave)
- 频率:< 2MHz
- 特性:有绕射能力
- 距离:数百或数千 km
- 应用:AM 广播

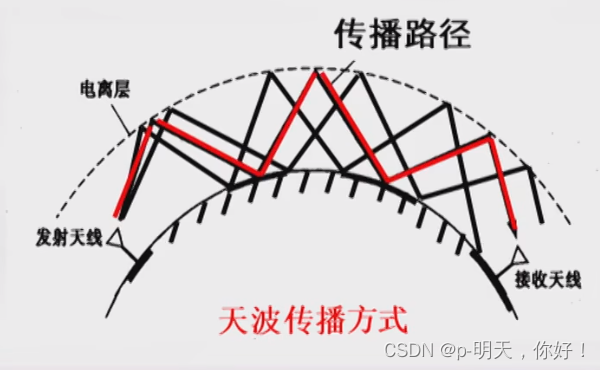
2、天波(sky-wave)
- 频率:2~30 MHz
- 特性:被电离层反射
- 距离:约 4000 km(一跳)
- 用于:远程、短波通信
3、视线传播(line-of-sight)
①、相关特性
- 频率:> 30 MHz
- 特征:直线传播、穿透电离层
- 用途:超短波和微波通信、卫星和外太空通信
- 距离:与天线高度 h 有关
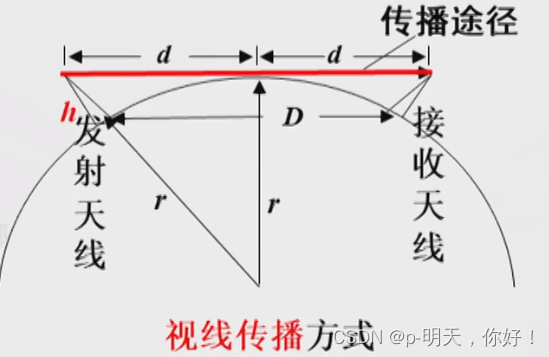
h = D 2 8 r ≈ D 2 50 ( m ) h=\frac{D^2}{8r}\approx\frac{D^2}{50}(m) h=8rD2≈50D2(m)
D D D 为收发天线间距离( k m km km), r = 6370 k m r=6370km r=6370km, r r r 是地球半径
例如设收发天线的架设高度均为 40 m 40m 40m,则最远通信距离为 D = 44.7 k m D=44.7km D=44.7km
②、增大视线传播距离的其他途径
- 微波中继(微博接力)
- 卫星中继(静止卫星、移动卫星)
- 平流层通信
<1>、微波中继
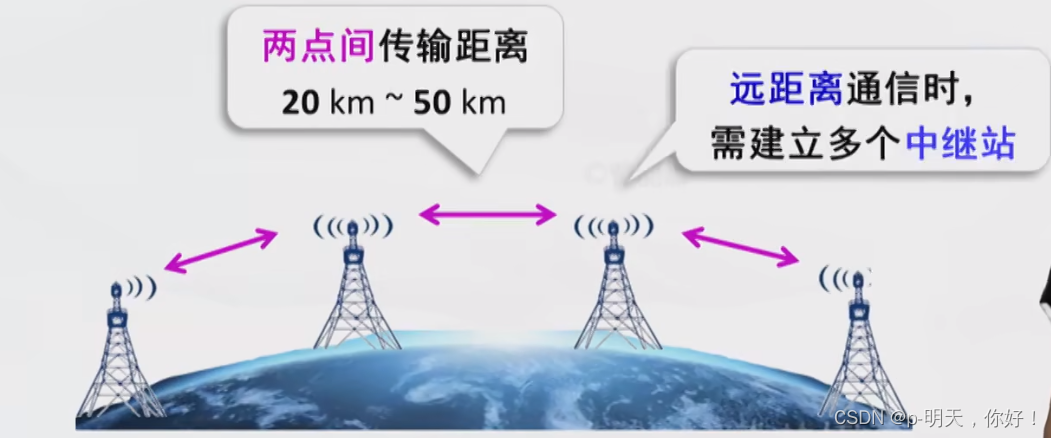
<2>、卫星中继

优点:通信容量大,传输质量稳定, 传输距离远,覆盖区域广
缺点:传输时延大,信号衰减大, 造价高。
四、随参信道的特性与影响
随参信道:指的是传输特性随时间随机变化的信道
如短波电离层反射、各种散射信道、移动通信信道等
1、随参信道的特性
- 衰减随时间变化
- 时延随时间变化
- 多径传播
多径传播:发端的信号经过了多条路径到达了接收端,或者说接收信号是多条路径下来的合成信号。
由于每条路径对信号的衰减和时延随机变化,因此,多径传播现象对信号会带来严重的影响
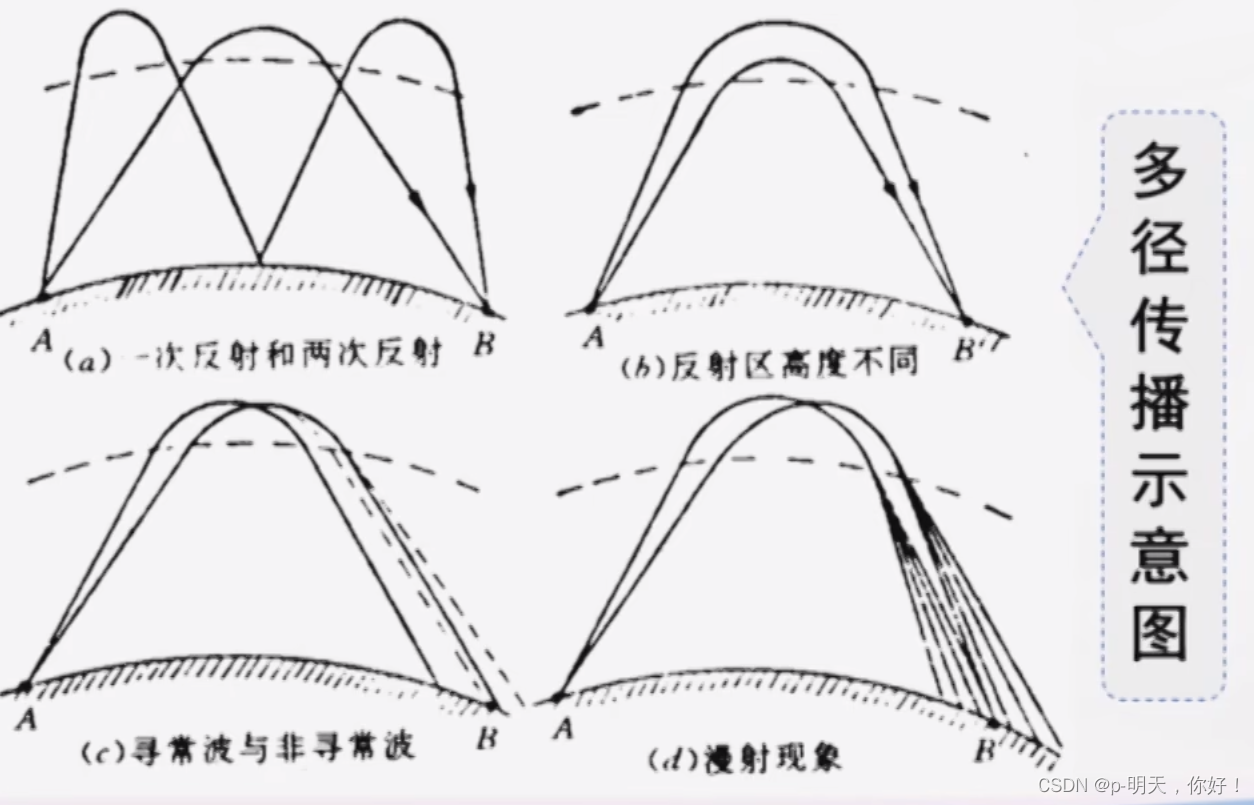
2、多径传播对于宽带信号的影响
①、频率选择性衰落
- 传输零点位置:衰减最小
- 传输极点位置
信道对不同频率的信号成分有不同的衰减,且随时间变化
τ \tau τ为两条路径的相对时延差
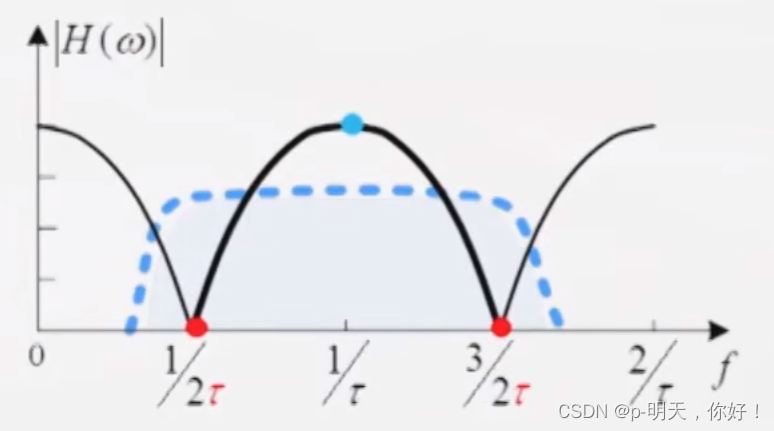
结论①:多径传播使信号产生瑞利型衰落与频率弥散
结论②:多径传播造成频率选择性衰减
②、避免频率选择性衰落的方法
- 信道相关带宽: Δ f = 1 / τ \Delta f=1/\tau Δf=1/τ ——相邻传输零点的频率间隔
- 应使信道带宽 B s B_s Bs小于 Δ f \Delta f Δf,工程经验公式: B s = ( 1 / 3 B_s=(1/3 Bs=(1/3~ 1 / 5 ) Δ f 1/5)\Delta f 1/5)Δf
- 数字信号的码元宽度: T s = ( 3 T_s=(3 Ts=(3~ 5 ) τ 5)\tau 5)τ ——> R B = 1 T s R_B=\frac{1}{T_s} RB=Ts1(码元速率决定了数字信号占用的带宽)注:数字信号码元宽度 T s T_s Ts
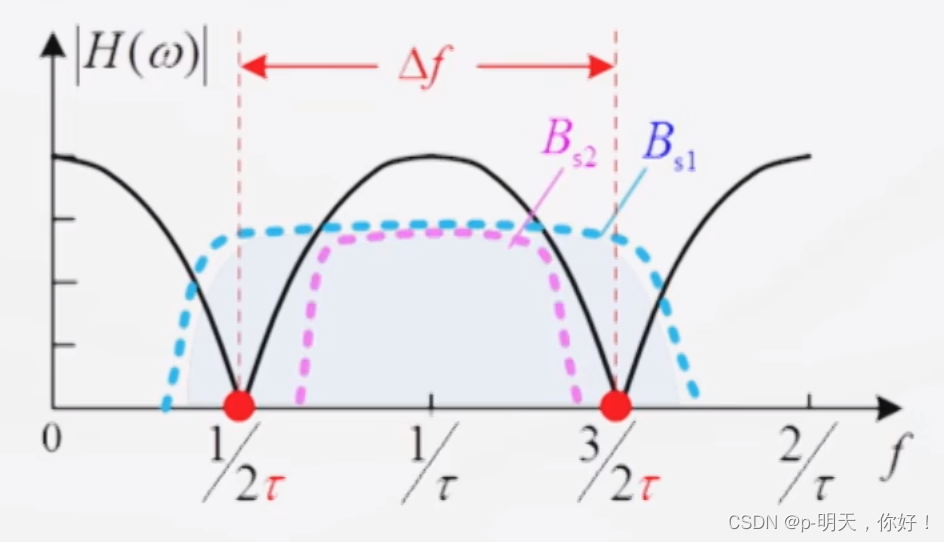
这就意味着要限制码元速率对传输高速的数字信号时,频选衰落将会引起严重的码间串扰,但是实际中我们需要高速传输,那么高速传输必然会引起频选衰落,怎么办呢?=====>OFDM —— 减小频率选择性衰落的有效措施之一。
3、OFDM —— 减小频率选择性衰落的有效措施之一
①、定义
正交频分复用(Orthogonal Frequency Division Multiplexing),是 4G 的关键技术之一
—— 具有较强的抗多径传播和抗频率选择性衰落的能力,以及较高的频谱利用率,在高速无线通信系统中得到了广泛应用。
T s T_s Ts短 ---- 占用 B B B大
②、思想
思想:将信道分成 N 个正交子信道,将高速数据信号经过串/并转换成 N 路并行的低速子数据流,分别调制到各子载波上并行传输。
T s T_s Ts长 ---- 占用 B B B小
因占用带宽小,所以子信道的信号带宽 < 信道的相关带宽,所以每个子信道上可以看成是平坦型衰落,从而消除码间串扰,子信道的均衡也相对容易。
五、信道容量
1、无扰信道的容量——奈奎斯特定理
奈奎斯特证明,对于一个带宽为 B 赫兹的无扰信道,其所能承载的最大信息速率(信道容量)为:
C = 2 B log 2 M ( b / s ) C=2B\log_2^M(b/s) C=2Blog2M(b/s)
B B B —— 信道带宽(Hz)
M M M —— 信号电平数(进制数)
例使用 B = 3000 H z B=3000Hz B=3000Hz 的话音信道通过调制解调器来传输数字信息:
- 若 M = 2 M=2 M=2 则 C = 6000 ( b / s ) C= 6000 (b/s) C=6000(b/s)
- 若 M = 4 M=4 M=4 则 C = 12000 ( b / s ) C= 12000 (b/s) C=12000(b/s)
- 若 M = 8 M=8 M=8 则 C = 18000 ( b / s ) C=18000 (b/s) C=18000(b/s)
给定B,增加M ,可提高C
给定M,B加倍,则C加倍
2、有扰信道的容量——香农公式
①、定义
信息论之父——香农证明,对于加性高斯白噪声(AWGN)信道,其无差错传输的最大平均信息速率(信道容量)为:
C = B log 2 1 + S N ( b / s )——香农公式 C=B\log_2^{1+\frac{S}{N}}(b/s)——香农公式 C=Blog21+NS(b/s)——香农公式
等价式:
C = B log 2 1 + S n 0 B ( b / s ) C=B\log_2^{1+\frac{S}{n_0B}}(b/s) C=Blog21+n0BS(b/s)
式中, S S S——信号平均功率(W); B B B——信道带宽(Hz)
n 0 n_0 n0——噪声单边功率谱密度(W/Hz); N = n 0 B N=n_0B N=n0B——噪声功率(W)
②、结论
- 信道容量 C C C 依赖于 B 、 S B、S B、S 和 n 0 n_0 n0 三要素。
- B B B一定,增大 S S S 或减小 n 0 n_0 n0( 即提高 S / N S/N S/N),可增大 C C C
若 S → ∞ S \to \infty S→∞,则 C → ∞ C\to \infty C→∞
若 n 0 → 0 n_0 \to 0 n0→0,则 C → ∞ C\to \infty C→∞ - S / n 0 S/n_0 S/n0,一定,当 B → ∞ B \to \infty B→∞ 时, C C C 趋于有限定值:
lim B → ∞ C = lim B → ∞ B l o g 2 1 + S n 0 B ≈ 1.44 S n 0 \lim_{B \to \infty} C= \lim_{B \to \infty} Blog_2^{1+\frac{S}{n_0B}}\approx1.44\frac{S}{n_0} B→∞limC=B→∞limBlog21+n0BS≈1.44n0S
信道容量极限
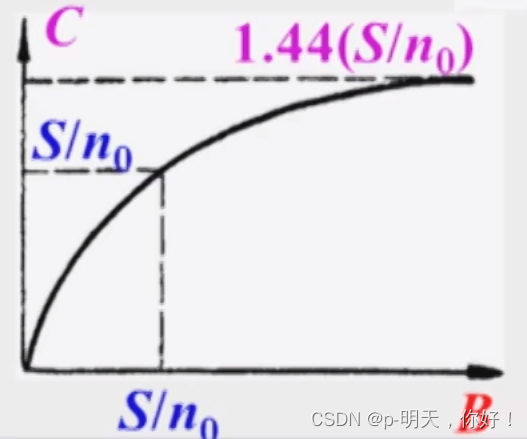
- 若实际信息速率 R b ≤ C R_b \leq C Rb≤C,则总能找到一种信道编码方式,实现无差错传输,若 R b > C R_b > C Rb>C,则不可能实现无差错传输。
③、应用
通过 B B B 与 S / N S/N S/N 的互换,可保证一定的信道容量 C C C:
- 增加 B B B,可以换取 S / N S/N S/N 的降低——宇宙飞行,深空探测,CDMA
- 提高 S / N S/N S/N,可以换取 B B B 的减小——有线载波电话,频带拥挤场合
3、联系
下面例题将香农公式和奈奎斯特定理两者结合的一个例子:

评注:在香农公式给定的信道容量之下,由奈奎斯特定理确定信号信号电平数 M
我的qq:2442391036,欢迎交流!
相关文章:

电磁波定义、特性以及信道相关知识
文章目录 前言一、电磁波的定义、特性、波谱1、电磁波的特性2、电磁波谱的划分及用途 二、地球大气层的结构三、电磁波的传播方式1、地波(ground-wave)2、天波(sky-wave)3、视线传播(line-of-sight)①、相关…...
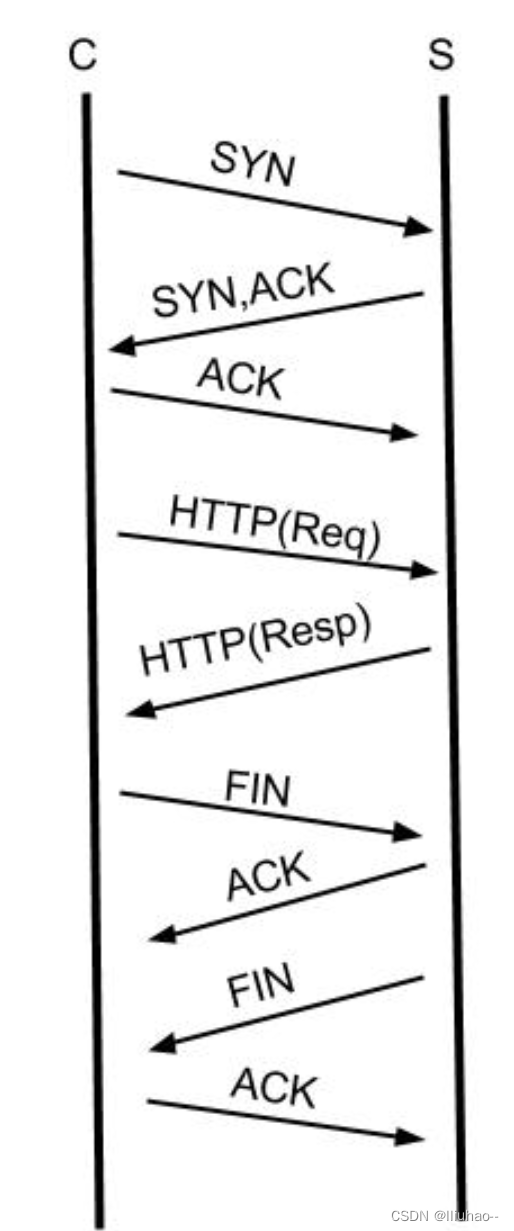
TCP KeepAlive与HTTP Keep-Alive
TCP KeepAlive与HTTP Keep-Alive TCP KeepAliveHTTP Keep-AliveTCP服务器怎么检测客户端断开连接 TCP KeepAlive TCP连接建立之后,如果应用程序或者上层协议一直不发送数据,或者隔很长时间才发送一次数据,那么TCP需要判断是应用程序掉线了还…...
)
SkyWalking链路追踪-Agent (代理人)
基础概念: SkyWalking链路追踪代理(SkyWalking Tracing Agent)是一种用于收集和传输链路追踪数据的工具。它与应用程序一起部署,并通过自动或手动方式来收集关于应用程序中的请求路径和操作的信息。该代理将收集到的数据发送到Sky…...
多线程案例 | 单例模式、阻塞队列、定时器、线程池
多线程案例 1、案例一:线程安全的单例模式 单例模式 单例模式是设计模式的一种 什么是设计模式? 设计模式好比象棋中的 “棋谱”,红方当头炮,黑方马来跳,针对红方的一些走法,黑方应招的时候有一些固定的…...

C++文件操作
1.写文件 //文件操作 #include<fstream> int main() {//写文件//路径 -- 此路径没有就生成给文件 string filePath R"(E:\项目\test.txt)";//打开文件 ios::app在后面追加内容 啥也不跟是覆盖写入ofstream fout(filePath, ios::app);//检查是否打开成功if (…...
 公式过大,需要调小字体,同时公式编号字体不变的方法)
overleaf(latex) 公式过大,需要调小字体,同时公式编号字体不变的方法
提问:用latex编辑的双列排版的论文中,如果一个包含矩阵的公式中,矩阵过大,导致超出列的范围,一般该如何调整呢? 回答:如果你在LaTeX中的双列排版中遇到了一个矩阵过大而导致超出列范围的问题&a…...

flink采用thrift读取tablets一个天坑
原先的配置 [INFO] StarRocksSourceBeReader [open Scan params.mem_limit 8589934592 B] [INFO] StarRocksSourceBeReader [open Scan params.query-timeout-s 600 s] [INFO] StarRocksSourceBeReader [open Scan params.keep-alive-min 100 min] [INFO] StarRocksSourceBeRea…...

Android 面试题 异常捕获 四
🔥 为什么要捕获奔溃 🔥 因为在开发或者测试阶段不能做到100%的问题解决,因为 app 上线之后会有你想不到的各种各样的使用的场景,而发生问题时用户只能描述一下怎么怎么怎么就出现了问题。也许反馈到开发这边可以100%复现那就可以…...
自动化测试:让软件测试更高效更愉快!
谈谈那些实习测试工程师应该掌握的基础知识(一)_什么时候才能变强的博客-CSDN博客https://blog.csdn.net/qq_17496235/article/details/131839453谈谈那些实习测试工程师应该掌握的基础知识(二)_什么时候才能变强的博客-CSDN博客h…...

SpringCloud学习—Feign负载均衡
Feign简介 Feign是声明式Web Service客户端,它让微服务之间的调用变得更简单,类似controller调用service。SpringCloud集成了Ribbon和Eureka,可以使用Feigin提供负载均衡的http客户端 只需要创建一个接口,然后添加注解即可。使用…...
5G时代的APP开发:机遇与挑战
APP开发是互联网行业中的重要组成部分,随着5G时代的到来,移动 APP开发也迎来了新的机遇和挑战。 5G时代不仅会为移动 APP开发带来新的发展机遇,也会给移动 APP开发带来新的挑战。对于企业和开发者而言,5G时代带来的机遇和挑战是并…...
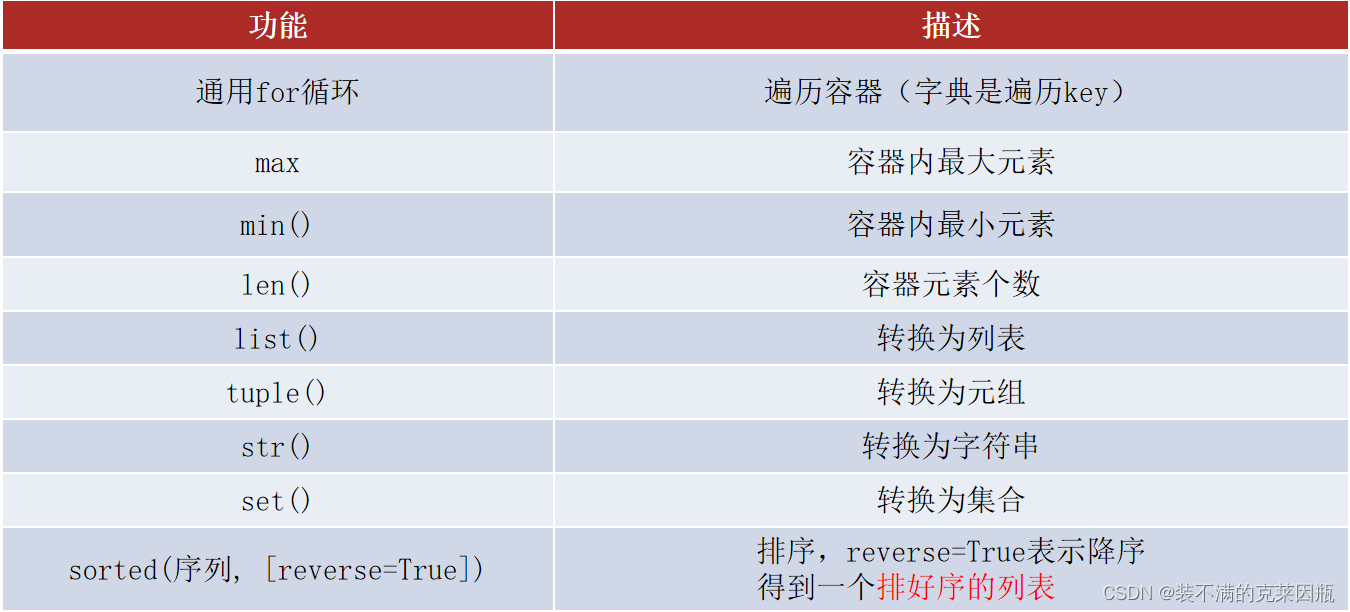
Python基础入门教程(上)
目录 一、你好Python 1.1、Python安装 win版 Linux版 1.2、第一个Python程序 二、Python基本语法 2.1、字面量 2.2、注释 2.3、变量 2.4、数据类型 type()函数 字符串类型的不同定义方式 2.5、数据类型转换 编辑 2.6、标识符 2.7、运算符 2.8、字符串扩展 …...
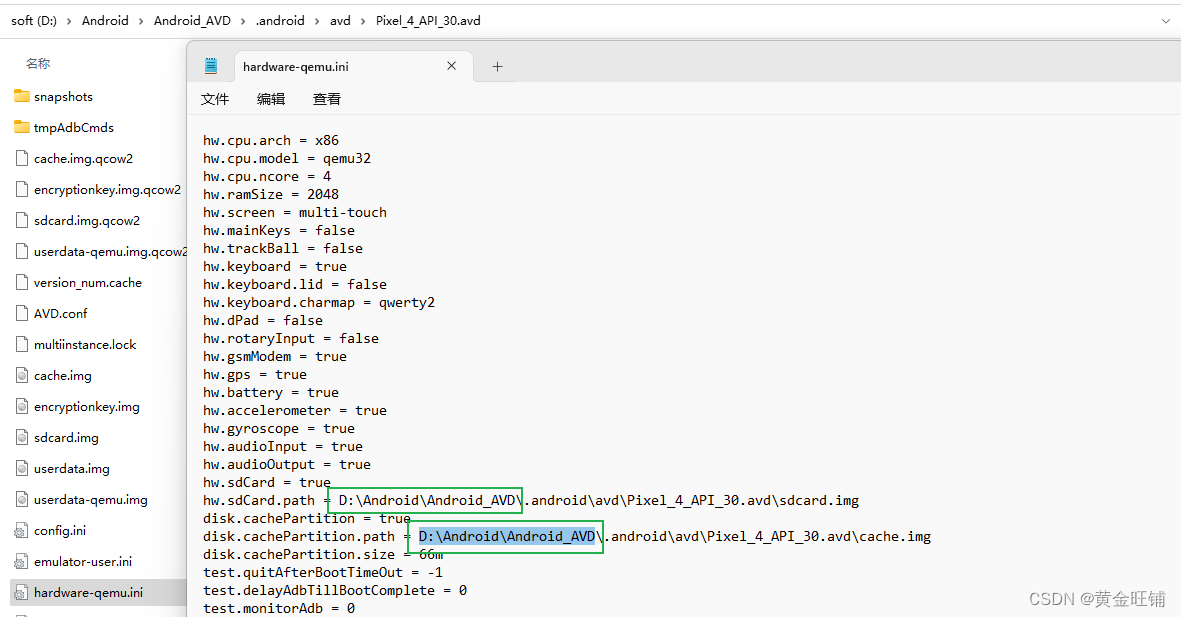
【环境配置】Windows下WSL将ubuntu挪位置-系统盘清理
问题–垃圾太多,系统盘空间占用太大 最近 C 盘空间暴涨,用工具 WinDirStat-强烈推荐的工具 查看发现 WSL 子系统占用了6个多 G 的空间,遂想办法挪个位置; 【关键字】将 Windows 里的子系统挪到非系统盘 D 盘; 解决 打…...

【前端知识】React 基础巩固(三十三)——Redux的使用详解
React 基础巩固(三十三)——Redux的使用详解 Redux的使用详解 针对React 基础巩固(三十二)中的案例,我们希望抽取页面中共有的代码(例如下方的代码),使用高阶组件统一拦截。 constructor() {super();this.…...

如何进行SQL优化
一、SQL优化的主要步骤 在应用的的开发过程中,由于初期数据量小,开发人员写 SQL 语句时更重视功能上的实现,但是当应用系统正式上线后,随着生产数据量的急剧增长,很多 SQL 语句开始逐渐显露出性能问题,对生…...

docker 部署 mysql8.0 无法访问
文章目录 🗽先来说我的是什么情况🪁问题描述🪁解决方法:✔️1 重启iptables✔️2 重启docker 🪁其他有可能连不上的原因✔️1 客户端不支持caching_sha2_password的加密方式✔️2 my.conf 配置只有本机可以访问 &#…...
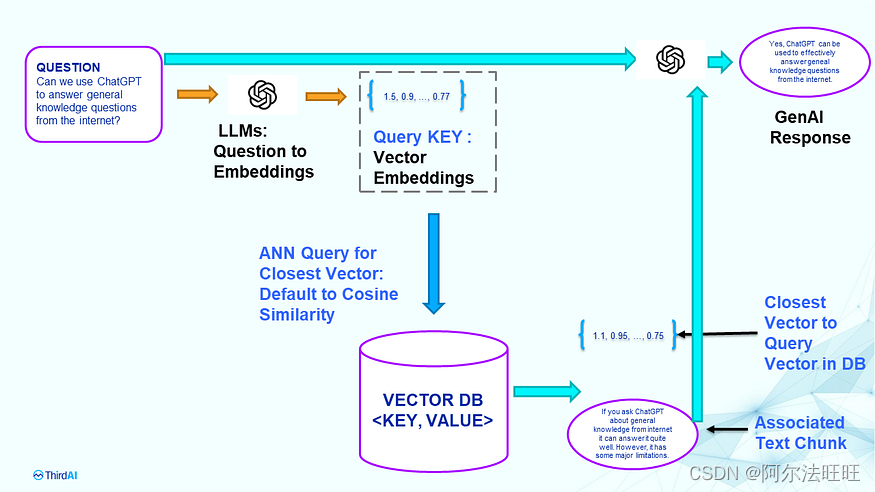
理解构建LLM驱动的聊天机器人时的向量数据库检索的局限性 - (第1/3部分)
本博客是一系列文章中的第一篇,解释了为什么使用大型语言模型(LLM)部署专用领域聊天机器人的主流管道成本太高且效率低下。在第一篇文章中,我们将讨论为什么矢量数据库尽管最近流行起来,但在实际生产管道中部署时从根本…...

IntersectionObserver实现小程序长列表优化
IntersectionObserver实现小程序长列表优化 关于 IntersectionObserver 思路 这里以一屏数据为单位【一个分页的10条数据,最好大于视口高度】, 监听每一屏数据和视口的相交比例,即用户能不能看到它 只将可视范围的数据渲染到页面上&#x…...
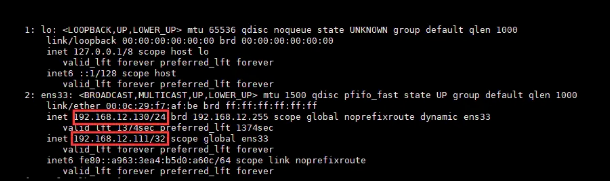
Nginx动静分离、资源压缩、负载均衡、黑白名单、防盗链等实战
一、前言 Nginx是目前负载均衡技术中的主流方案,几乎绝大部分项目都会使用它,Nginx是一个轻量级的高性能HTTP反向代理服务器,同时它也是一个通用类型的代理服务器,支持绝大部分协议,如TCP、UDP、SMTP、HTTPS等。 二、…...

Rust之枚举与模式匹配
枚举类型,简称枚举,允许列举所有可能的值来定义一个类型。 1、定义枚举: 枚举类型:已知所有可能的值,并且所有值的出现是互斥的,即每次只能取一种可能的值,才使用枚举类型。 示例:…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
