【学习笔记】「ROI 2018 Day 2」无进位加法
先放一个大佬的博客:「loj - 2850」「ROI 2018 Day 2」无进位加法
用数据结构来优化搜索🤔
神一样的 Kidulthood 考场上就已经意识到了这道题的正解是搜索😅
考虑搜索过程的本质🤔
首先是找到最小的满足 t i + i t_i+i ti+i最大的点 i i i,发现对于 p ≠ t i + i p\ne t_i+i p=ti+i的情况都可以直接回溯掉,否则先把 [ 1 , i − 1 ] [1,i-1] [1,i−1]全部删掉,然后将其后继插入到序列当中。可以分析出递归的次数其实就是最开始选定的那个串的长度。
那么分两种情况:
1.1 1.1 1.1 成功,那么其实就不需要回溯了
1.2 1.2 1.2 不成功,那么刚开始选定的那个串就会被删掉(换句话说是把 [ 1 , i ] [1,i] [1,i]全部删掉)
这样复杂度 O ( L log L ) O(L\log L) O(LlogL)。
感性理解
remark \text{remark} remark 这玩意写成代码确实比较抽象。。。
#include<bits/stdc++.h>
#define fi first
#define se second
#define ll long long
#define pb push_back
#define db double
#define inf 0x3f3f3f3f
using namespace std;
const int N=6e5+5;
int n,m,maxL,sz[N],pre[N];
string nums[N];
vector<int>each[N];
pair<int,int>a[N];
vector<int>ps[N];
vector<int>nxt[N];
int res[N];
set<int>s;
struct node{pair<int,int>max;int add;
}t[N<<2];
void add(int p,int x){t[p].add+=x,t[p].max.fi+=x;
}
void pushdown(int p){if(t[p].add){add(p<<1,t[p].add),add(p<<1|1,t[p].add),t[p].add=0;}
}
void pushup(int p){t[p].max=max(t[p<<1].max,t[p<<1|1].max);
}
void build(int p,int l,int r){if(l==r){if(a[l].se==sz[a[l].fi]-1)t[p].max=make_pair(pre[l]+a[l].se,m-l+1),s.insert(l);else t[p].max=make_pair(pre[l]+a[l].se-inf,m-l+1);return;}int mid=l+r>>1;build(p<<1,l,mid),build(p<<1|1,mid+1,r);pushup(p);
}
void modify(int p,int l,int r,int ql,int qr,int x){if(ql>qr)return;if(ql<=l&&r<=qr){add(p,x);return;}int mid=l+r>>1;pushdown(p);if(ql<=mid)modify(p<<1,l,mid,ql,qr,x);if(mid<qr)modify(p<<1|1,mid+1,r,ql,qr,x);pushup(p);
}
void update(int p,int l,int r,int x,int y){if(l==r){t[p].max.fi+=y;return;}int mid=l+r>>1;pushdown(p);x<=mid?update(p<<1,l,mid,x,y):update(p<<1|1,mid+1,r,x,y);pushup(p);
}
int solve(int p){if(t[1].max.fi<=0)return 1;vector<int>tmp;int p2=t[1].max.fi,u=m-t[1].max.se+1,cnt=0;if(p2>p)return 0;while(*s.begin()!=u){cnt++;int cur=*s.begin();modify(1,1,m,cur,m,-1);update(1,1,m,cur,-inf);tmp.pb(cur);s.erase(cur);}modify(1,1,m,u,m,-1);update(1,1,m,u,-inf);s.erase(u);for(int i=p2-1;i>=p2-cnt;i--)res[i]=1;int x=a[u].fi,y=a[u].se,r=-1;if(~nxt[x][y]){r=ps[x][nxt[x][y]];modify(1,1,m,r,m,1);update(1,1,m,r,inf);s.insert(r);}if(solve(p2-1-cnt))return res[p2-cnt-1]=1;if(~r){modify(1,1,m,r,m,-1);update(1,1,m,r,-inf);s.erase(r);}if(p2==p){for(auto cur:tmp){modify(1,1,m,cur,m,1);update(1,1,m,cur,inf);s.insert(cur);}modify(1,1,m,u,m,1);update(1,1,m,u,inf);s.insert(u);return 0;}res[p2]=1;return solve(p2-cnt);
}
int low[N],seq[N],cnt;
bool cmp(int x,int y){return low[x]<low[y];
}
int main(){ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<=n;i++){cin>>nums[i],sz[i]=nums[i].size(),maxL=max(maxL,sz[i]);ps[i].resize(sz[i]),nxt[i].resize(sz[i]);for(int j=0;j<sz[i];j++)nums[i][j]-='0';reverse(nums[i].begin(),nums[i].end());int lst=-1;for(int j=0;j<sz[i];j++){if(nums[i][j]==1){each[j].pb(i);nxt[i][j]=lst;lst=j;}}}m=0;//基数排序for(int i=0;i<maxL;i++){cnt=0;for(auto e:each[i]){low[e]=(nxt[e][i]==-1)?0:ps[e][nxt[e][i]];if(nums[e][i]==1)low[e]+=inf;seq[++cnt]=e;}sort(seq+1,seq+1+cnt,cmp);for(int j=1;j<=cnt;j++){a[++m]=make_pair(seq[j],i);ps[seq[j]][i]=m;}}reverse(a+1,a+1+m);for(int i=1;i<=m;i++)ps[a[i].fi][a[i].se]=i;for(int i=1;i<=m;i++)pre[i]=pre[i-1]+(a[i].se==sz[a[i].fi]-1);build(1,1,m);solve(inf);int tp=maxL+n-1;while(tp&&res[tp]==0)tp--;for(int i=tp;i>=0;i--)cout<<res[i];
}
相关文章:

【学习笔记】「ROI 2018 Day 2」无进位加法
先放一个大佬的博客:「loj - 2850」「ROI 2018 Day 2」无进位加法 用数据结构来优化搜索🤔 神一样的 Kidulthood 考场上就已经意识到了这道题的正解是搜索😅 考虑搜索过程的本质🤔 首先是找到最小的满足 t i i t_ii tii最大…...
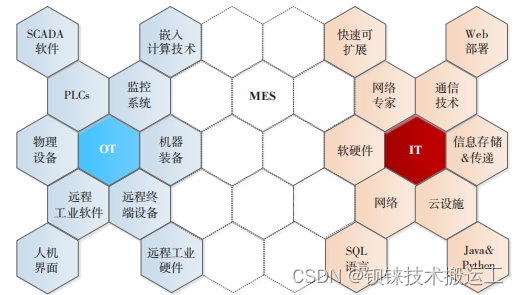
分布式I/O,IT和OT融合少不了它
长期以来信息技术IT和操作运营技术OT是相互隔离的,随着大数据分析和边缘计算业务的对现场级实时数据的采集需求,IT和OT有了逐渐融合的趋势。IT与OT融合,它赋予工厂的管理者监控运行和过程的能力大为增强,甚至可以预测到可能发生的…...

主干网络篇 | YOLOv8 更换主干网络之 VanillaNet |《华为方舟实验室最新成果》
论文地址:https://arxiv.org/pdf/2305.12972.pdf 代码地址:https://github.com/huawei-noah/VanillaNet 在基础模型的核心是“多样性即不同”,这一哲学在计算机视觉和自然语言处理方面取得了惊人的成功。然而,优化和Transformer模型固有的复杂性带来了挑战,需要转向简洁性…...

AD20. 如何给元器件设计、添加3D模型
Altium Designer学习笔记 - 00.目录 零. 前言 本文以HF46F继电器为例展示设计、添加元器件3D模型的流程,其他元器件类似。 一. 操作步骤 从下图可以看到此时继电器还没有添加3D模型: 1. 获取元器件尺寸 这里通过查找元器件的数据手册可以…...

C++笔记之vector的底层实现和扩容机制
C笔记之vector的底层实现和扩容机制 1. 先申请内存空间,内存空间容量变成原来的n倍(一般是原来的两倍) 2. 将原本容器中的数据拷贝到新的内存空间中 3. 释放原来的内存空间 4. 将数组指针指向新容器的内存空间 code review! 文章目录 C笔记之vector的底层实现和扩…...

JavaSE - Sting类
目录 一. 字符串的定义 二. String类中的常用方法 1. 比较两个字符串是否相等(返回值是boolean类型) 2. 比较两个字符串的大小(返回值是int类型) 3. 字符串查找 (1)s1.charAt(index) index:下标&…...

zotero+overleaf插入参考文献
zotero导出参考献bib文件 overleaf上传此biib文件 后续添加package,输出参考文献,添加引用参考http://t.csdn.cn/bC245 默认导出的bib文件信息臃肿,使用插件设置,安装过程参考http://t.csdn.cn/4HcBm…...
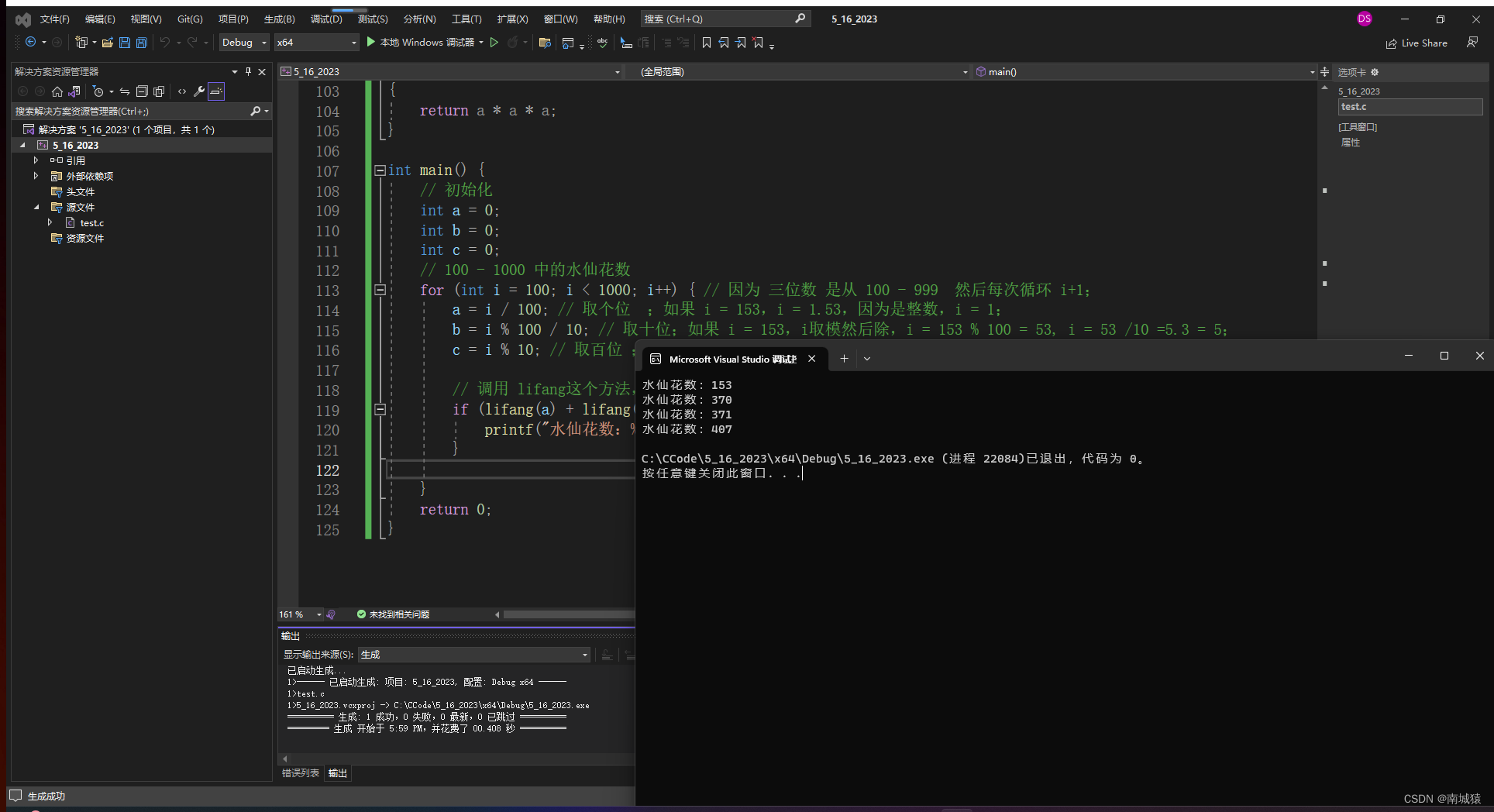
C语言每天一练----输出水仙花数
题目:请输出所有的"水仙花数" 题解:所谓"水仙花数"是指一个3位数,其各位数字立方和等于该数本身。 例如, 153是水仙花数, 因为153 1 * 1 * 1 5 * 5 * 5 3 * 3 * 3" #define _CRT_SECURE_NO_WARNINGS 1#include <stdio.h&g…...
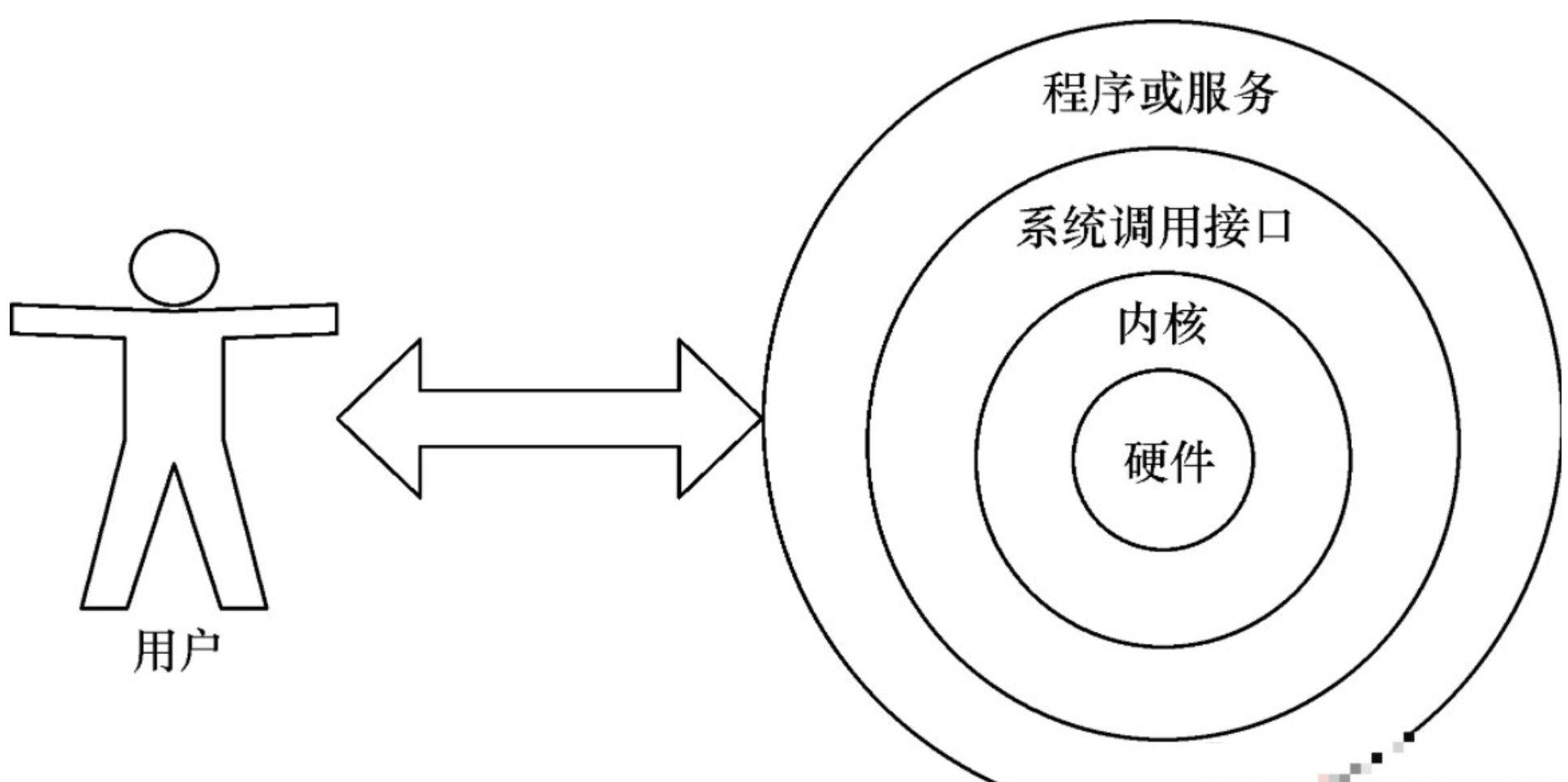
Linux-Shell
1.什么是Bash shell(壳) Bash Shell是一个命令解释器,它在操作系统的最外层,负责用户程序与内核进行交互操作的一种接口,将用户输入的命令翻译给操作系统,并将处理后的结果输出至屏幕。 通过xshell连接,就是打开了一…...
Python读取csv、Excel文件生成图表
简介 本文章介绍了通过读取 csv 或 Excel 文件内容,将其转换为折线图或柱状图的方法,并写入 html 文件中。 目录 1. 读取CSV文件 1.1. 生成折线图 1.1.1. 简单生成图表 1.1.2. 设置折线图格式 1.2. 生成柱状图 1.2.1. 简单生成图表 1.2.2. 设置柱…...

虚拟机中Linux的IP地址配置详解
目录 第一章、虚拟机中Linux的IP地址配置详解1.1)什么是IP地址1.2)如何查看自己电脑ip地址1.3)虚拟机NAT模式中Linux的IP地址设置有什么要求 第二章、使用Linux中的编辑命令进行网卡信息文件的配置 友情提醒 先看文章目录,大致了…...

Codeforces Round 889 (Div. 2) 题解
晚上睡不着就来总结一下叭~(OoO) 赛后榜(希望不要被Hack...Orz) 终榜!!! 瞬间的辉煌(呜呜呜~) 先不放图了。。怕被dalaoHack...呜呜呜~ 总结 7.29半夜比赛,本来是不想打的,感觉最近做的题太多…...
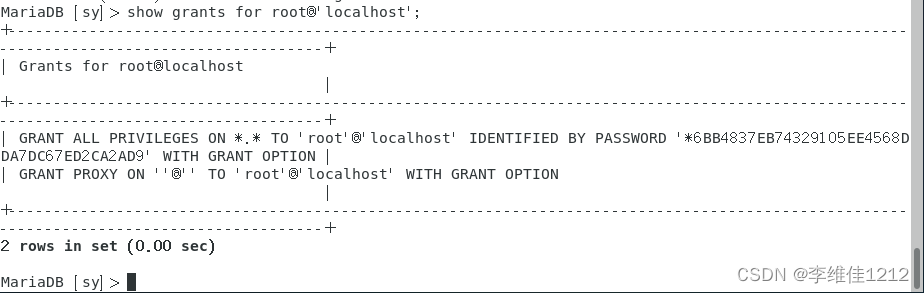
系统学习Linux-MySQL用户权限管理(三)
一、用户权限管理概述 数据库用户权限管理是数据库系统中非常重要的一个方面,它用于控制不同用户访问和操作数据库的权限范围。数据库用户权限管理可以保护敏感数据和数据库结构,确保只有被授权的用户才可以操作和使用数据库,防止数据被修改…...

【雕爷学编程】MicroPython动手做(02)——尝试搭建K210开发板的IDE环境4
7、使用串口工具 (1)连接硬件 连接 Type C 线, 一端电脑一端开发板 查看设备是否已经正确识别: 在 Windows 下可以打开设备管理器来查看 如果没有发现设备, 需要确认有没有装驱动以及接触是否良好 (2&a…...

阿里云NVIDIA A100 GPU云服务器性能详解及租用费用
阿里云GPU服务器租用费用表包括包年包月、一个小时收费以及学生GPU服务器租用费用,阿里云GPU计算卡包括NVIDIA V100计算卡、T4计算卡、A10计算卡和A100计算卡,GPU云服务器gn6i可享受3折,阿里云百科分享阿里云GPU服务器租用表、GPU一个小时多少…...

数字身份、分布式存储、跨链技术等将如何推动Web3数据的发展?
Web3数据是基于区块链技术、去中心化、可信任的数据,具有较高的安全性和可信度。随着Web3.0时代的到来,Web3数据将会在金融、物联网、医疗、教育、政务等领域发挥重要的作用。其中,数字身份、分布式存储、跨链技术等将会是Web3数据发展的重要…...

Ubuntu 新增2T 硬盘,配置自动挂载
Ubuntu 台式机内存太小了,增加了一块 2T 的硬盘,记录下配置过程: 查看硬盘信息 可以看出,我电脑当前有三块硬盘: (1) /dev/nvme0n1 系统盘,256 G,分了两个区 /dev/nvme0n…...
Windows下安装HBase
Windows下安装HBase 一、HBase简介二、HBase下载安装包三、环境准备3.1、 JDK的安装3.2、 Hadoop的安装 四、HBase安装4.1、压缩包解压为文件夹4.2、配置环境变量4.3、%HBASE_HOME%目录下新建临时文件夹4.4、修改配置文件 hbase-env.cmd4.4.1、配置JAVA环境4.4.2、set HBASE_MA…...
在家构建您的迷你 ChatGPT
这篇文章分为三个部分;他们是: 什么是指令遵循模型?如何查找遵循模型的指令构建一个简单的聊天机器人废话不多说直接开始吧!!! 什么是指令遵循模型? 语言模型是机器学习模型,可以根…...

Cisco IOS操作(红茶三杯CCNA)
Cisco路由器组件 CPU:执行指令RAM:断电内容丢失 运行操作系统运行配置文件IP路由表ARP缓存数据包缓存区 ROM:保存开机自检软件,存储路由器的启动引导程序 bootstrap指令基本的自检软件迷你版IOS 非易失RAM(NVRAM&#…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...

HTML中各种标签的作用
一、HTML文件主要标签结构及说明 1. <!DOCTYPE html> 作用:声明文档类型,告知浏览器这是 HTML5 文档。 必须:是。 2. <html lang“zh”>. </html> 作用:包裹整个网页内容,lang"z…...
