排序算法汇总
每日一句:你的日积月累终会成为别人的望尘莫及
目录
常数时间的操作
选择排列
冒泡排列
【异或运算】
面试题:
1)在一个整形数组中,已知只有一种数出现了奇数次,其他的所有数都出现了偶数次,怎么找到出现了奇数次的数?(要求时间复杂度O(N),空间复杂度O(1))
2)在一个整形数组中,已知有两种数出现了奇数次,其他的所有数都出现了偶数次,怎么找到这两种数?(要求时间复杂度O(N),空间复杂度O(1))
插入排序
二分法的详解与扩展
1)在一个有序数组中,找某个数是否存在
2)在一个有序数组中,找大于等于某个数最左侧的位置
局部最小值问题
在一个数组中arr无序,且任何两个相邻的数不相等,求局部最小
对数器的概念和使用
递归行为和递归行为时间复杂度的估算
归并排序
小和问题
在一个数组中,每一个数左边比当前数小的数累加起来,叫做这个数组的小和。求一个数组的小和。
例:[1,2,4,3,5],1左边比1小的数没有;2左边比2小的数,1;4左边比4小的数,1,2;3左边比3小的数,1,2;5左边比5小的数1,2,4,3;
所以小和为1+1+2+1+2+1+2+4+3=17
荷兰国旗问题
问题一
给定一个数组arr,和一个数num,请把小于等于num的数放在数组的左边,大于num的数放在数组的右边.要求额外空间复杂度O(1),时间复杂度O(N)
问题二
给定一个数组arr和一个数num请把小于num的数放在数组的左边,等于num的数放在数组的中间,大于num的数放在数组的右边.要求额外空间复杂度O(1),时间复杂度O(N).
不改进的快速排序
堆
heapinsert过程
heapify过程
堆排序
已知一个几乎有序的数组,几乎有序是指[如果把数组排好顺序的话,每个元素移动的距离可以不超过K,并且k相对于数组来说比较小]请选择一个合适的排序算法针对这个数据进行排序。
比较器的使用
桶排序思想下的排序
排序算法的稳定性及其汇总
常数时间的操作
一个操作如果和样本的数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作
时间复杂度为一个算法流程中,常数操作数量的一个指标。
常用O(读作bigO)来表示。具体来说,先要对一个算法流程非常熟悉,然后去写出这个算法流程中,发生了多少常数操作,进而总结出常数操作数量的表达式。
在表达式中,只要高阶项,不要低阶项的系数,剩下的部分如果为f(N),那么时间复杂度为O(f(N))
评价一个算法流程的好坏,先看时间复杂度的指标,然后再分析不同数据样本下的实际运行时间,也就是“常数项时间”
数组、+、-、*、/、位运算是常数操作
链表不是常数操作

额外空间复杂度
指这个流程需要多少额外空间才能支持计算下来
———————————————————————————————————————
选择排列
冒泡排列
相邻比较,谁大谁往右移

【异或运算】
1)0^N=N N^N=0
2) 满足交换、结合律
a^b=b^a (a^b)^c=a^(b^c)
(抖机灵法:不用额外分配一块内存空间)
int a=甲 int b=乙
a=a^b; ——>a=甲^乙 b=乙;
b=a^b; ——>a=甲^乙 b=甲^乙^乙=甲^0=甲;
a=a^b; ——>a=甲^乙^甲=乙^0=乙 b=甲;
前提:a和b在内存里是两块独立的区域,i位置不能等于j位置,否则会异或成0
面试题:
1)在一个整形数组中,已知只有一种数出现了奇数次,其他的所有数都出现了偶数次,怎么找到出现了奇数次的数?(要求时间复杂度O(N),空间复杂度O(1))

———————————————————————————————————————
2)在一个整形数组中,已知有两种数出现了奇数次,其他的所有数都出现了偶数次,怎么找到这两种数?(要求时间复杂度O(N),空间复杂度O(1))

- 先让eor从头异或到尾,结尾时eor=a^b≠0
- a和b一定有一位不一样的,假设第8位因为把整个数组分成2类;第1类:第8位是0;第2类:第8位是1
eor1只异或第8位是1的数;eor1为a或b
3.eor^eor1为另一个a或b
把一个不为0的数最右侧的1,提取出来的操作:int rightone=eor&(~eor+1);

插入排序
时间复杂度O(![]() ),额外空间复杂度O(1)
),额外空间复杂度O(1)
算法流程按照最差情况来估计时间复杂度

数据状况不同会导致算法流程的时间复杂度不一样
选择排序和冒泡排序算法和数据状况无关


二分法的详解与扩展
1)在一个有序数组中,找某个数是否存在
-
2)在一个有序数组中,找大于等于某个数最左侧的位置

局部最小值问题
在一个数组中arr无序,且任何两个相邻的数不相等,求局部最小

优化方向1)数据状况2)问题标准
对数器的概念和使用
- 有一个你想要测的方法a
- 实现复杂度不好但是容易实现的方法b
- 实现一个随机样本产生器
- 把方法a和方法b跑相同的随机样本,看得到的结果是否一样
- 如果有一个随机样本使得比对结果不一致,打印样本进行人工干预,改对方法a或者方法b
- 当样本数量很多时对比测试依然正确,可以确定方法a已经正确
递归行为和递归行为时间复杂度的估算
用递归方法找一个数组中的最大值,系统上到底怎么做的?
Master公式的使用
T(N)=a*T(Nb![]() )+O(
)+O(![]() )
)
 >d 复杂度为O(
>d 复杂度为O( )
)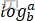 =d 复杂度为O(
=d 复杂度为O( )
) <d 复杂度为O(
<d 复杂度为O(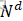 )
)
中点:mid=L+![]() =L+(R-L)>>1
=L+(R-L)>>1

归并排序
- 整体就是一个简单递归,左边排好序,右边排好序,让其整体有序
- 让其整体有序的过程用了外排序方法
- 利用master公式来求解时间复杂度
- 归并排序的实质
时间复杂度O(![]() ),额外空间复杂度O(N)
),额外空间复杂度O(N)


选择、冒泡、插入O(![]() )浪费了大量的比较行为
)浪费了大量的比较行为

归并排序比较行为没有被浪费
比较行为被留下来了,变成了一个整体有序的部分,信息往下传递
—————————————————————————————————————
归并排序的扩展
小和问题
在一个数组中,每一个数左边比当前数小的数累加起来,叫做这个数组的小和。求一个数组的小和。
例:[1,2,4,3,5],1左边比1小的数没有;2左边比2小的数,1;4左边比4小的数,1,2;3左边比3小的数,1,2;5左边比5小的数1,2,4,3;
所以小和为1+1+2+1+2+1+2+4+3=17

逆序对问题
在一个数组中,左边的数如果比右边的数大,则这两个数构成一个逆序对,请打印所有逆序对。
例如:数组[3,2,4,5,0],存在逆序对[3,2]、[3,0]、[2,0]、[4,0]、[5,0]
—————————————————————————————————————
荷兰国旗问题
问题一
给定一个数组arr,和一个数num,请把小于等于num的数放在数组的左边,大于num的数放在数组的右边.要求额外空间复杂度O(1),时间复杂度O(N)

问题二
给定一个数组arr和一个数num请把小于num的数放在数组的左边,等于num的数放在数组的中间,大于num的数放在数组的右边.要求额外空间复杂度O(1),时间复杂度O(N).

—————————————————————————————————————
不改进的快速排序
1)把数组范围中的最后一个数作为划分值,然后把数组通过荷兰国旗问题分成三个部分
左侧<划分值、中间==划分值、右侧>划分值
2)对左侧范围和右侧范围,递归执行
分析:
- 划分值越靠近两侧,复杂度越高;划分值越靠近中间,复杂度越低
- 可以轻而易举的举出最差的例子,所以不改进的快速排序时间复杂度为O(
)
快排额外空间复杂度O(
)


堆
- 堆结构就是用数组实现的完全二叉树结构
- 完全二叉树中如果每棵子树的最大值都在顶部就是大根堆
- 完全二叉树中如果每棵子树的最小值都在顶部就是小根堆
- 堆结构的heapInsert(一路往上走)与heapify(一路往下走)操作
- 堆结构的增大和减少
- 优先级队列结构就是堆结构
heapinsert过程

heapify过程

堆排序
1.先让整个数组都变成大根堆结构,建立堆的过程;
- )从上到下的方法,时间复杂度O(N
)
- 从下到上的方法,时间复杂度O(N)
2.把堆的最大值和堆末尾的值交换,然后减少堆的大小,之后,再去调整堆,一直周而复始,时间复杂度O(N
)
3. 堆的大小减小成0之后,排序完成


堆排序扩展题目
已知一个几乎有序的数组,几乎有序是指[如果把数组排好顺序的话,每个元素移动的距离可以不超过K,并且k相对于数组来说比较小]请选择一个合适的排序算法针对这个数据进行排序。

小根堆在Java中优先级队列意思
PriorityQueue<Integer> heap=new PriorityQueue<>();
1.扩容怎么办?
扩容次数O(
)水平
每次扩容O(N)水平
整体O(
)水平
单位平均下来O(
)水平
2.系统写好的堆,不支持已经实现了的堆用很轻的代价,使某一结构变值,调整自己写的堆
比较器的使用
- 比较器的实质就是重载比较运算符
- 比较器可以很好的应用在特殊标准的排序上
- 比较器可以很好的应用在根据特殊标准排序的结构上
———————————————————————————————————————
不基于比较的排序都是根据数据状况做的排序
桶排序思想下的排序
- 计数排序
- 基数排序
分析
- 桶排序思想下的排序都是不基于比较的排序
- 时间复杂度O(N),额外空间复杂度O(N)
- 应用范围有限,需要样本的数据状况满足桶的划分


排序算法的稳定性及其汇总
同样值的个体之间,如果不因为排序而改变相对次序,就是这个排序是有稳定性的;否则就没有
不具有稳定性的排序:选择排序、快速排序、堆排序;
具备稳定性的排序:冒泡排序、插入排序、归并排序、一切桶排序思想下的排序
[相等的时候不让交换,保持了稳定性]
目前没有找到时间复杂度O(![]() ),额外空间复杂度O(1),又稳定的排序
),额外空间复杂度O(1),又稳定的排序
选择排序
从0~N-1位置上选一最小值,放0位置上……
冒泡排序
0~1上比较交换,1~2,2~3,3~4,4~5,5位置排好
0~1上比较交换,1~2,2~3,3~4 ,4位置排好
……
插入排序
0~0有序
0~1交换、有序
0~2交换、有序
| 时间复杂度 | 额外空间复杂度 | 稳定性 | |
| 选择 | O( | O(1) | × |
| 冒泡 | O( | O(1) | √ |
| 插入 | O( | O(1) | √ |
| 归并 | O( | O(N) | √ |
| 快排 | O( | O( | × |
| 堆 | O( | O(1) | × |
常见的坑
- 归并排序的额外空间复杂度可以变为O(1),但非常难,不需要掌握,有兴趣可以搜“归并排序内部缓存法”
- “原地归并排序”的帖子都是垃圾,会让归并排序的时间复杂度变成O(
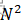 )
) - 快排可以做到稳定性,但非常难,不需要掌握,可以搜“01 stable sort”
- 所有的改进都不重要,因为目前没有找到时间复杂度O(
 ),额外空间复杂度O(1),又稳定的排序
),额外空间复杂度O(1),又稳定的排序 - 有一道题目是奇数放在数组左边,偶数放在数组右边,还要求原始的相对次序不变,碰到这个问题,可以怼面试官
工程上对排序的改进
- 充分利用O(
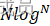 )和O(
)和O(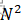 )排序各自的优势
)排序各自的优势 - 稳定性的考虑
| 大样本量时 | 调度 快排 O( |
| 小样本量时 | 插入 O( |
相关文章:
排序算法汇总
每日一句:你的日积月累终会成为别人的望尘莫及 目录 常数时间的操作 选择排列 冒泡排列 【异或运算】 面试题: 1)在一个整形数组中,已知只有一种数出现了奇数次,其他的所有数都出现了偶数次,怎么找到…...

cocos2d 中UserDefault在windows平台下的路径问题
在使用cocos2dx c开发项目时,通常使用cocos自带的UserDefault来存储一些项目所用到的一些配置信息:如游戏的音量,游戏的闯关数等... 但是windows平台下,测试发现如果用户的帐户名使用是中文,在启动程序时会报错&#…...

ChatGPT与高等教育变革:价值、影响及未来发展
最近一段时间,ChatGPT吸引了社会各界的目光,它可以撰写会议通知、新闻稿、新年贺信,还可以作诗、写文章,甚至可以撰写学术论文。比尔盖茨、马斯克等知名人物纷纷为此发声,谷歌、百度等知名企业纷纷宣布要提供类似产品。…...

Matlab Image Processing toolbox 下载安装方法
当安装好Matlab之后,发现没有Image Processing toolbox这个图像处理工具箱 从新安装一遍, 选上 Image Processing toolbox 但是不用选matlab即可 1.找到之前安装时的Setup安装程序包,按照之前安装Matlab步骤,到选择需要安装的Ma…...
?如何使用消息键进行消息顺序性保证?)
什么是消息键(Key)?如何使用消息键进行消息顺序性保证?
消息键(Key)是Kafka消息的一个可选属性,用于标识消息的逻辑关联关系。每条消息可以携带一个关键字作为其键,这个键可以是字符串、整数等数据类型。 使用消息键可以在Kafka中实现消息的顺序性保证,具体方式如下&#x…...
慎思笃行,兴业致远:金融行业的数据之道
《中庸》中说,“博学之,审问之,慎思之,明辨之,笃行之”。这段话穿越千年,指引着中国千行百业的发展。对于金融行业来说,庞大的数据量可以说是“博学”的来源。但庞大的数据体量,既是…...

Git-分支管理
文章目录 1.分支管理2.合并冲突3.合并模式4.补充 1.分支管理 Git分支管理是指在Git版本控制系统中,使用分支来管理项目的不同开发线路和并行开发的能力。通过分支,开发者可以在独立的环境中进行功能开发、bug修复等工作,而不会影响到主分支上…...
[Ubuntu 22.04] containerd配置HTTP方式拉取私仓Harbor
文章目录 1. 基础环境配置2. Docker安装3. 部署Harbor,HTTP访问4. 部署ContainerD5. 修改docker配置文件,向harbor中推入镜像6. 配置containerd6.1. 拉取镜像验证6.2. 推送镜像验证 1. 基础环境配置 [Ubuntu 22.04] 安装K8S基础环境准备脚本 2. Docker安…...

入门指南:深入解析OpenCV的copyTo函数及其与rect的应用场景
文章目录 导言copyTo函数的示例copyTo函数与rect的应用场景结论 导言 OpenCV是一个功能强大的开源计算机视觉库,广泛应用于图像处理和计算机视觉任务。在OpenCV中,copyTo函数是一个重要的图像处理函数,它允许我们在不同的图像之间复制像素数…...

2018年全国硕士研究生入学统一考试管理类专业学位联考写作试题——解析版
2018年1月真题 四、写作:第56~57小题,共65分。其中论证有效性分析30 分,论说文35分。 56.论证有效性分析: 分析下述论证中存在的缺陷和漏洞,选择若干要点,写一篇600字左右的文章,对该论证的有…...
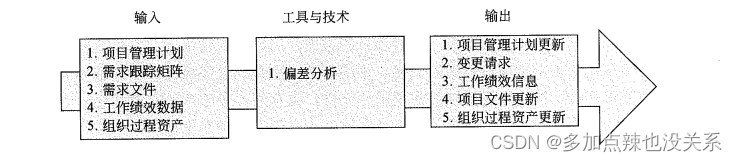
系统集成|第七章(笔记)
目录 第七章 范围管理7.1 项目范围管理概念7.2 主要过程7.2.1 规划范围管理7.2.2 收集需求7.2.3 定义范围7.2.4 创建工作分解结构 - WBS7.2.5 范围确认7.2.6 范围控制 上篇:第六章、整体管理 第七章 范围管理 7.1 项目范围管理概念 概述:项目范围管理就…...
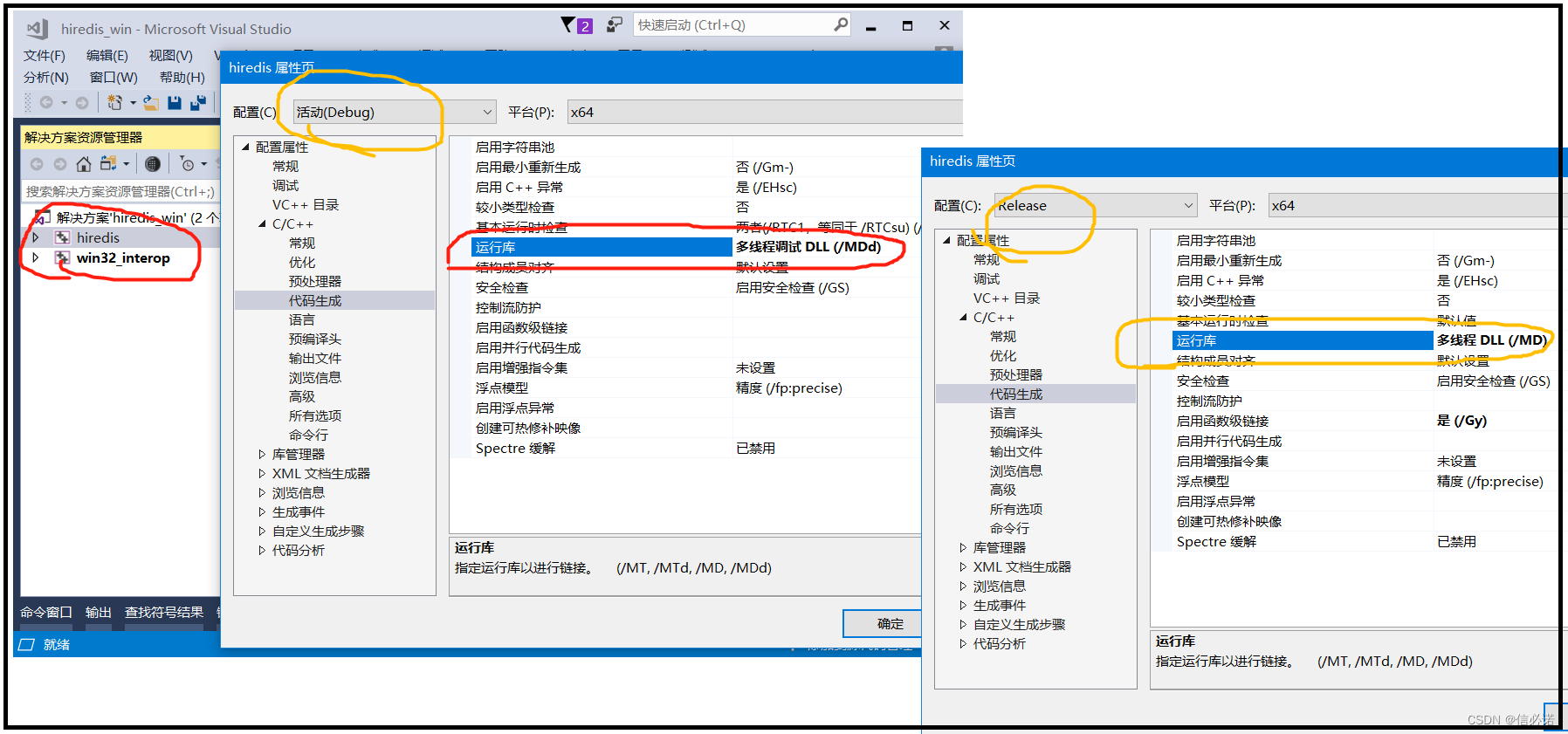
Qt —— Vs2017编译hiredis源码并测试调用(附调用hiredis库源码)
下载hiredis源码 编译hiredis源码 1、解压下载的hiredis源码包,如图使用Vs2017打开hiredis_win.sln 2、如下两图,Vs2017打开.sln后点击升级。 分别对两个工程的debug、release进行配置。Debug配置为多线程调试DLL(MDd)、Release配置为多线程DLL(/MD),这样做是为了配合被调用…...

深入理解设计模式:设计模式定义、设计原则以及组织编目
文章目录 一、设计模式1.1 设计模式的起源1.2 设计模式的定义1.3 记录要素1.4 合理使用模式 二、设计模式的六大原则2.1 开闭原则(Open-Closed Principle, OCP)2.1.1 定义2.1.2 原则分析2.1.3 开闭原则的意义所在 2.2 单一职责原则(Single Responsibility Principle, SRP)2.4.1…...
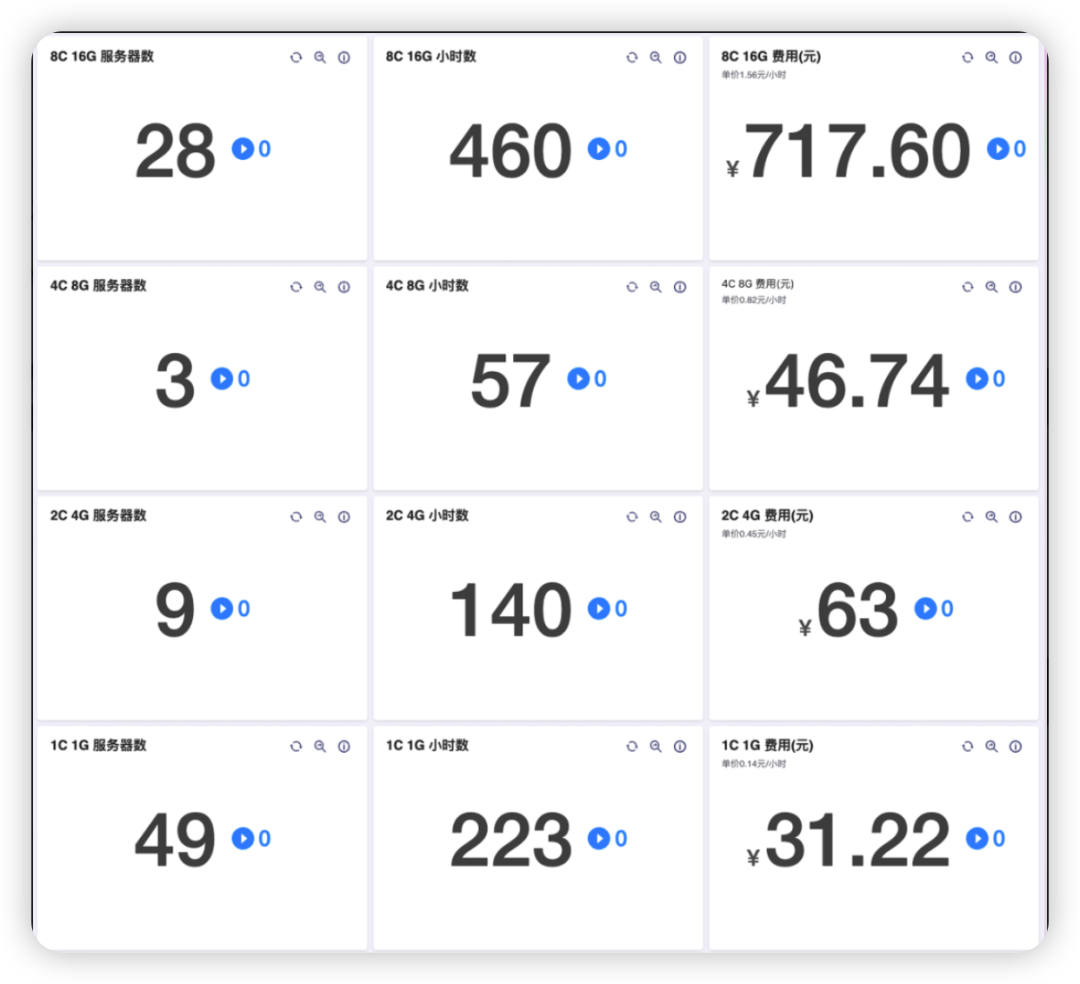
鸿鹄协助管理华为云与炎凰Ichiban
炎凰对华为云的需求 在炎凰日常的开发中,对于服务器上的需求,我们基本都是采用云服务。目前我们主要选择的是华为云,华为云的云主机比较稳定,提供的云主机配置也比较多样,非常适合对于不同场景硬件配置的需求ÿ…...
Vite创建Vue+TS项目引入文件路径报错
使用vite搭建vue3脚手架的时候,发现main.ts中引入App.vue编辑器会报错,但是不影响代码运行。 报错信息:TS2307: Cannot find module ‘./App.vue’ or its corresponding type declarations. 翻译过来是找不到模块或者相关的声明类型&#…...
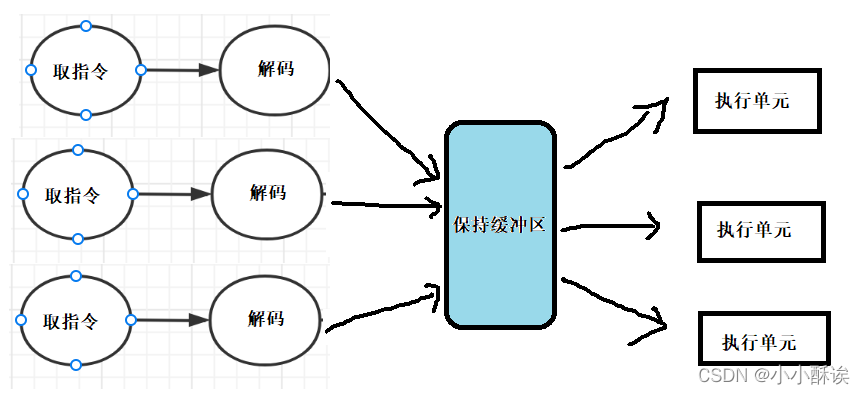
计算机里基本硬件的组成以及硬件协同
文章目录 冯诺依曼体系输入设备输出设备存储器运算器控制器协同工作的流程 冯诺依曼体系 世界上第一台通用计算机,ENIAC,于1946年诞生于美国一所大学。 ENIAC研发的前期,需要工作人员根据提前设计好的指令手动接线,以这种方式输入…...

2023软件设计师中级备考经验分享(文中有资料链接分享)
先摊结论吧,软考中级设计师备考只是备考半个月(期间还摆烂了几天),然而成绩如下: 我自己都没想到会这么好的成绩。。。 上午题:推荐把软考通APP里的历年真题刷3-4遍,直接刷真题,然后…...
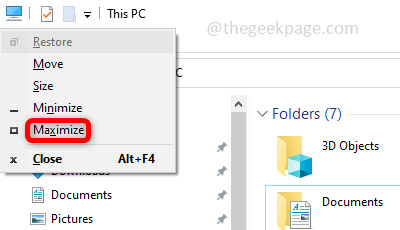
Windows 10 中无法最大化任务栏中的程序
方法1:仅选择选项 PC 屏幕 如果您使用双显示器,有时这可能会发生在您的 1 台计算机已插入但您正在访问的应用程序正在另一台计算机上运行的情况下,因此您看不到任何选项。因此,请设置仅在主计算机上显示显示的 PC 屏幕选项。 第…...

【iOS】KVOKVC原理
1 KVO 键值监听 1.1 KVO简介 KVO的全称是Key-Value Observing,俗称"键值监听",可以用于监听摸个对象属性值得改变。 KVO一般通过以下三个步骤使用: // 1. 添加监听 [self.student1 addObserver:self forKeyPath:"age"…...

当机器人变硬核:探索深度学习中的时间序列预测
收藏自:Wed, 15 Sep 2021 10:32:56 UTC 摘要:时间序列预测是机器学习和深度学习领域的一个重要应用,它可以用于预测未来趋势、分析数据模式和做出决策。本文将介绍一些基本概念和常用方法,并结合具体的案例,展示如何使…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...