数据结构:树的存储结构
学习树之前,我们已经了解了二叉树的顺序存储和链式存储,哪么我们如何来存储普通型的树结构的数据?如下图1:

如图1所示,这是一颗普通的树,我们要如何来存储呢?通常,存储这种树结构的数据的方法有3中:
- 双亲表示法。
- 孩子表示法。
- 孩子兄弟表示法。
双亲表示法
双亲表示法采用顺序表(也就是数组)存储普通树,核心思想:顺序存储各个节点的同时,给各个节点附加一个记录其父节点位置的变量。
注意:根结点没有父节点,因此根结点记录父节点位置的变量一般为-1。
例如,采用双亲表示法存储图1中的普通树,其存储状态如图2所示:

图2存储普通树转化为代码为:
#define MAX_SIZE 100//定义树中结点最大数量
typedef struct node{char data;//树中结点的数据int parent;//结点的父节点再数组中的位置下标
};typedef struct {node arr[MAX_SIZE];//存放树中所有结点int n;//节点数
}Tree;
因此,存储图1中普通树的实现代码为:
#include "iostream"using namespace std;
#define MAX_SIZE 100//定义树中结点最大数量
typedef struct node{char data;//树中结点的数据int parent;//结点的父节点再数组中的位置下标
};typedef struct {node arr[MAX_SIZE];//存放树中所有结点int n;//节点数
}Tree;Tree Init(Tree tree){cout << "请输入结点个数:" << endl;cin >> tree.n;cout << "请输入结点的值其双亲位于数组中的位置下标:" << endl;for(int i = 0; i < tree.n; i++){cin >> tree.arr[i].data >> tree.arr[i].parent;}return tree;
}void FindParent(Tree tree){char a;bool IsFind = false;cout << "请输入要查询的节点值:" << endl;cin >> a;for(int i = 0; i < tree.n; i++){if(tree.arr[i].data == a){IsFind = true;cout << a << "的父节点为" << tree.arr[tree.arr[i].parent].data << ",存储位置下标为" << tree.arr[i].parent << endl;break;}}
}
int main(){Tree tree;for(int i = 0; i < MAX_SIZE; i++){tree.arr[i].parent = -1;tree.arr[i].data = ' ';}tree = Init(tree);FindParent(tree);return 0;
}
程序运行实例:
请输入结点个数:
10
请输入结点的值其双亲位于数组中的位置下标:
R -1
A 0
B 0
C 0
D 1
E 1
F 3
G 6
H 6
K 6
请输入要查询的节点值:
C
C的父节点为R,存储位置下标为0
孩子表示法
孩子表示法是采用“顺序表+链表”的组合结构,其存储过程是:从树的根结点开始,使用顺序表依次存储树中各个节点,需要注意的是,与双亲表示法不同,孩子表示法会给各个节点配备一个链表,用于存储各个节点的孩子节点位于顺序表中的位置。
如果孩子没有叶子节点,则该节点的链表为空链表。
例如,使用孩子表示法存储图3a中的树,则最终存储状况如图3b所示:

代码实现如下:
#include "iostream"using namespace std;
#define MAX_SIZE 100//定义树中结点最大数量
typedef struct node{int child;//链表中每个结点存储的是数据再数组中存储的位置下标struct node *next;
};
typedef struct {char data;//结点的数据node * FirstChild;//孩子链表的头节点
}box;
typedef struct {box arr[MAX_SIZE];//存放树中所有结点int n, r;//节点数和树根的位置
}Tree;Tree Init(Tree tree){cout << "请输入结点个数:";cin >> tree.n;for(int i = 0; i < tree.n; i++){cout << "输入第" << i + 1 << "个节点的值:" ;cin >> tree.arr[i].data;tree.arr[i].FirstChild = new node;tree.arr[i].FirstChild->next = NULL;cout << "输入结点" << tree.arr[i].data << "的孩子结点的数量:";int num = 0;cin >> num;if(num != 0){node *p = tree.arr[i].FirstChild;for(int j = 0; j < num; j++){node *ptr = new node;ptr->next = NULL;cout << "输入第" << j + 1 << "个孩子节点在顺序表中的位置: ";cin >> ptr->child;p->next = ptr;p = p->next;}}}return tree;
}void FindKids(Tree tree, char ch){bool IsFind = false;for(int i = 0; i < tree.n; i++){if(tree.arr[i].data == ch){node *p = tree.arr[i].FirstChild->next;while(p){IsFind = true;cout << tree.arr[p->child].data;p = p->next;}break;}}
}
int main(){Tree tree;tree.r = 0;//默认根结点的下标为0for(int i = 0; i < MAX_SIZE; i++){tree.arr[i].FirstChild = NULL;}tree = Init(tree);FindKids(tree, 'F');//找出结点F的所有孩子结点return 0;
}
程序运行结果如下:
请输入结点个数:10
输入第1个节点的值:R
输入结点R的孩子结点的数量:3
输入第1个孩子节点在顺序表中的位置: 1
输入第2个孩子节点在顺序表中的位置: 2
输入第3个孩子节点在顺序表中的位置: 3
输入第2个节点的值:A
输入结点A的孩子结点的数量:2
输入第1个孩子节点在顺序表中的位置: 4
输入第2个孩子节点在顺序表中的位置: 5
输入第3个节点的值:B
输入结点B的孩子结点的数量:0
输入第4个节点的值:C
输入结点C的孩子结点的数量:1
输入第1个孩子节点在顺序表中的位置: 6
输入第5个节点的值:D
输入结点D的孩子结点的数量:0
输入第6个节点的值:E
输入结点E的孩子结点的数量:0
输入第7个节点的值:F
输入结点F的孩子结点的数量:3
输入第1个孩子节点在顺序表中的位置: 7
输入第2个孩子节点在顺序表中的位置: 8
输入第3个孩子节点在顺序表中的位置: 9
输入第8个节点的值:G
输入结点G的孩子结点的数量:0
输入第9个节点的值:H
输入结点H的孩子结点的数量:0
输入第10个节点的值:K
输入结点K的孩子结点的数量:0
找出节点 F 的所有孩子节点:GHK
使用孩子表示法存储的树结构,正好和双亲表示法相反,适用于 查找某个节点的孩子结点,不适用于查找父节点。
其实,我们也可以将双亲表示法和孩子表示法相互结合,就可以得到如图4所示:

使用图4结果存储普通树,技能快速找到指定节点的父节点,也能快速找到指定结点的孩子结点。
孩子兄弟表示法
孩子兄弟表示法:采用的是链式存储结构,其思想是,从树的根结点开始,依次用链表存储各个节点的孩子结点和兄弟节点。
所以,该链表中的结点包括3个部分,如图5所示:
- 结点的值。
- 指向孩子结点的指针。
- 指向兄弟结点的指针。

代码表示如下:
typedef struct node{char data;struct node *ForstChild, *NextSibling;
};
还是以图1为例,使用孩子兄弟表示法进行存储的结果如图所示:

由图我们可以发现,孩子兄弟表示法是用二叉树的左子树存储树的孩子结点,用右子树来存储兄弟结点。
孩子兄弟表示法可以作为将普通树转化为二叉树的最有效的方法,同时这个方法也被称之为“二叉树表示法”或者”二叉链表表示法“
相关文章:

数据结构:树的存储结构
学习树之前,我们已经了解了二叉树的顺序存储和链式存储,哪么我们如何来存储普通型的树结构的数据?如下图1: 如图1所示,这是一颗普通的树,我们要如何来存储呢?通常,存储这种树结构的数…...
Vue前端渲染blob二进制对象图片的方法
近期做开发,联调接口。接口返回的是一张图片,是对二进制图片处理并渲染,特此记录一下。 本文章是转载文章,原文章:Vue前端处理blob二进制对象图片的方法 接口response是下图 显然,获取到的是一堆乱码&…...
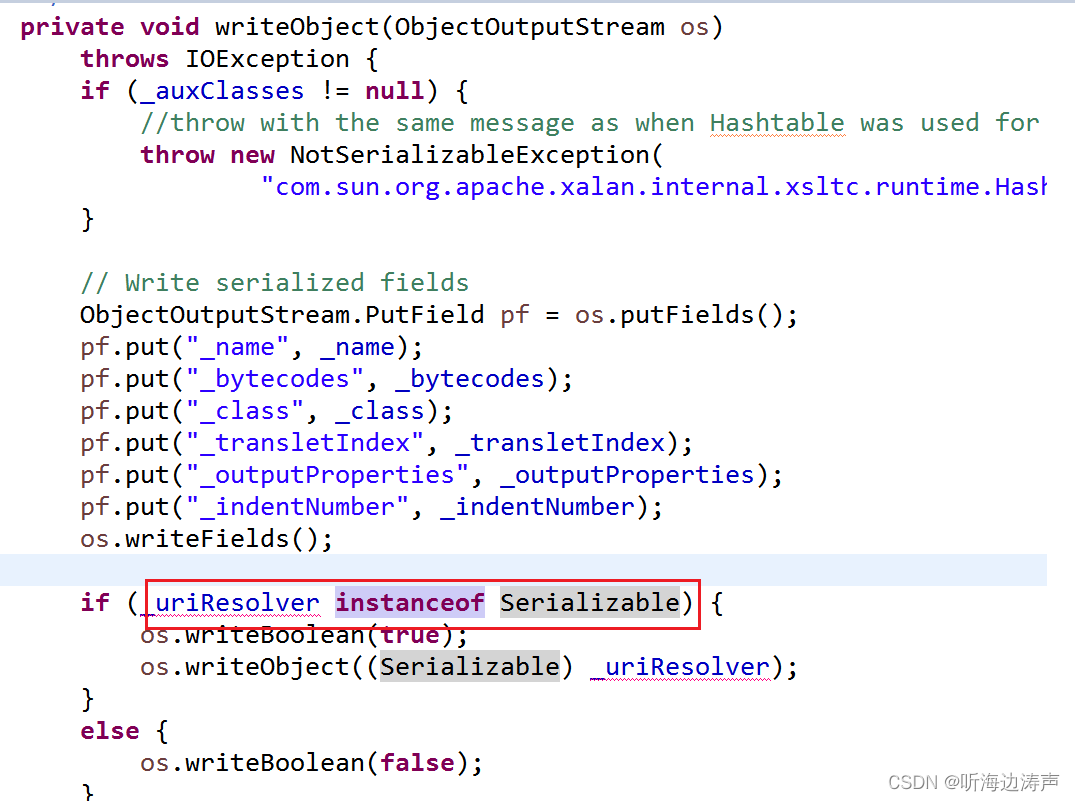
Java的标记接口(Marker Interface)
Java中的标记接口(Marker Interface)是一个空接口,接口内什么也没有定义。它标识了一种能力,标识继承自该接口的接口、实现了此接口的类具有某种能力。 例如,jdk的com.sun.org.apache.xalan.internal.xsltc.trax.Temp…...
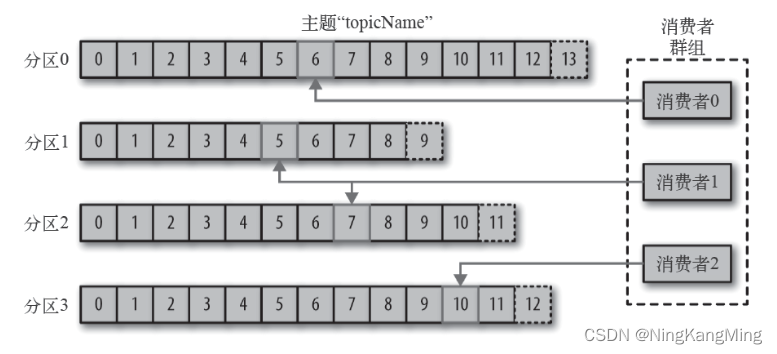
Kafka基础架构与核心概念
Kafka简介 Kafka是由Apache软件基金会开发的一个开源流处理平台,由Scala和Java编写。Kafka是一种高吞吐量的分布式发布订阅消息系统,它可以处理消费者在网站中的所有动作流数据。架构特点是分区、多副本、多生产者、多订阅者,性能特点主要是…...
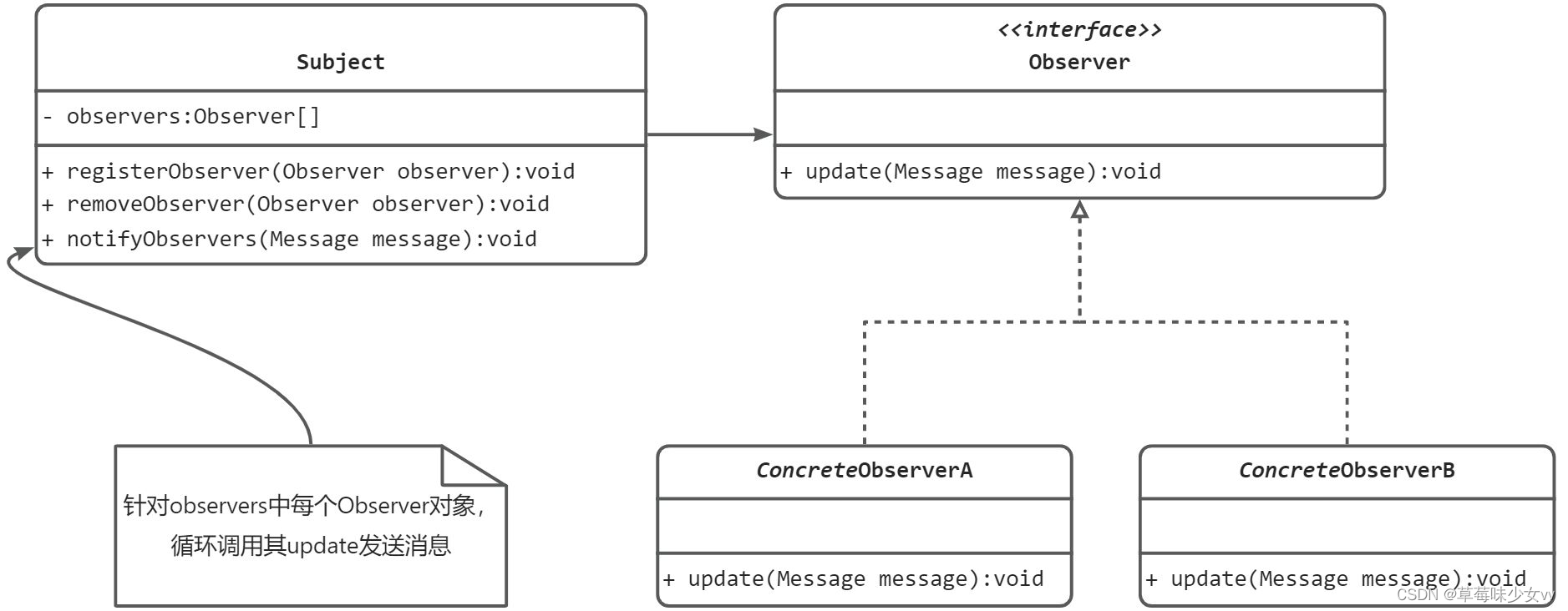
观察者模式与观察者模式实例EventBus
什么是观察者模式 顾名思义,观察者模式就是在多个对象之间,定义一个一对多的依赖,当一个对象状态改变时,所有依赖这个对象的对象都会自动收到通知。 观察者模式也称为发布订阅模式(Publish-Subscribe Design Pattern)࿰…...

科普 | OSI模型
本文简要地介绍 OSI 模型 1’ 2’ 3。 更新:2023 / 7 / 23 科普 | OSI模型 术语节点链路协议网络拓扑 概念作用结构应用层表示层会话层传输层网络层数据链路层物理层 数据如何流动OSI 和TCP/IP 的对应关系和协议参考链接 术语 节点 节点( Node &#…...

redis相关异常之RedisConnectionExceptionRedisCommandTimeoutException
本文只是分析Letture类型的Redis 池化连接出现的连接超时异常、读超时异常问题。 1.RedisConnectionException 默认是10秒。 通过如下可以配置: public class MyLettuceClientConfigurationBuilderCustomizer implements LettuceClientConfigurationBuilderCusto…...

Merge the squares! 2023牛客暑期多校训练营4-H
登录—专业IT笔试面试备考平台_牛客网 题目大意:有n*n个边长为1的小正方形摆放在边长为n的大正方形中,每次可以选择不超过50个正方形,将其合并为一个更大的正方形,求一种可行的操作使所有小正方形都被合并成一个n*n的大正方形 1…...
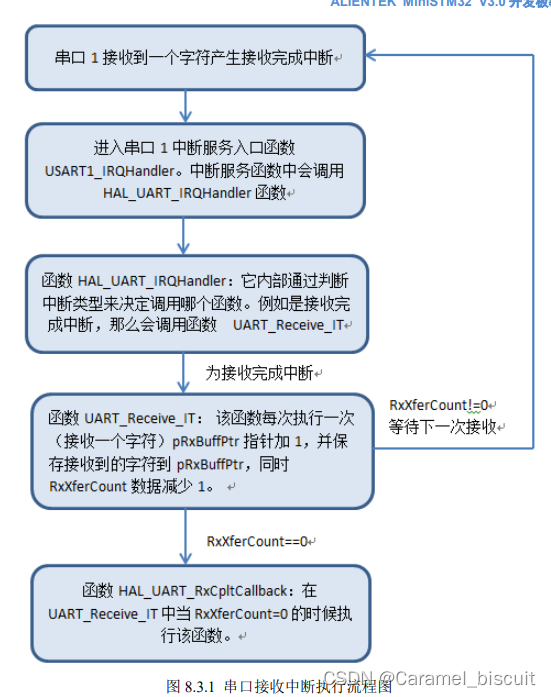
STM32 串口学习(二)
要用跳线帽将PA9与RXD相连,PA10与TXD相连。 软件设计 void uart_init(u32 baud) {//UART 初始化设置UART1_Handler.InstanceUSART1; //USART1UART1_Handler.Init.BaudRatebound; //波特率UART1_Handler.Init.WordLengthUART_WORDLENGTH_8B; //字长为 8 位数据格式U…...
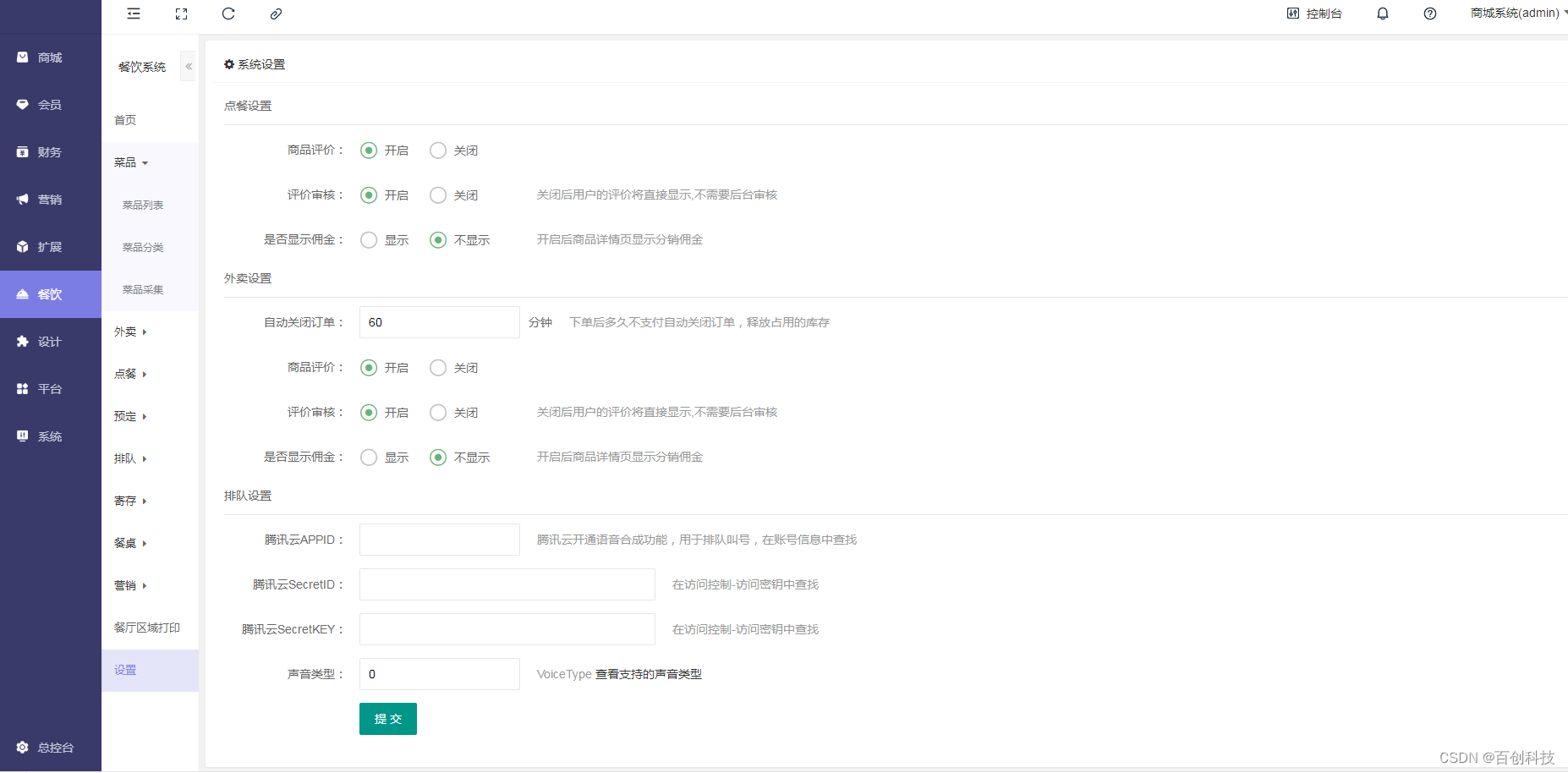
点大商城V2_2.5.0 全开源版 商家自营+多商户入驻 百度+支付宝+QQ+头条+小程序端+unipp开源前端安装测试教程
安装测试环境:Nginx 1.20PHP7.2MySQL 5.6 修复了无法上传开放平台问题 安装说明: 1、上传后端目录至网站 2、导入提供的数据库文件 3、修改数据库配置文件根目录下config.php,增加数据库用户名和密码 4、网站后台直接访问网址ÿ…...

“深入理解SpringBoot:从入门到精通“
标题:深入理解Spring Boot:从入门到精通 摘要:本文将介绍Spring Boot的基本概念和核心特性,并通过示例代码演示如何使用Spring Boot构建一个简单的Web应用程序。 1. 简介 Spring Boot是一个开源的Java框架,旨在简化基…...

PCB绘制时踩的坑 - SOT-223封装
SOT-223封装并不是同一的,细分的话可以分为两种常用的封装。尤其是tab脚的属性很容易搞错。如果你想着用tab脚连接有属性的铺铜,来提高散热效率,那么你一定要注意你购买的器件tab脚的属性。 第一种如下图,第1脚为GND,第…...
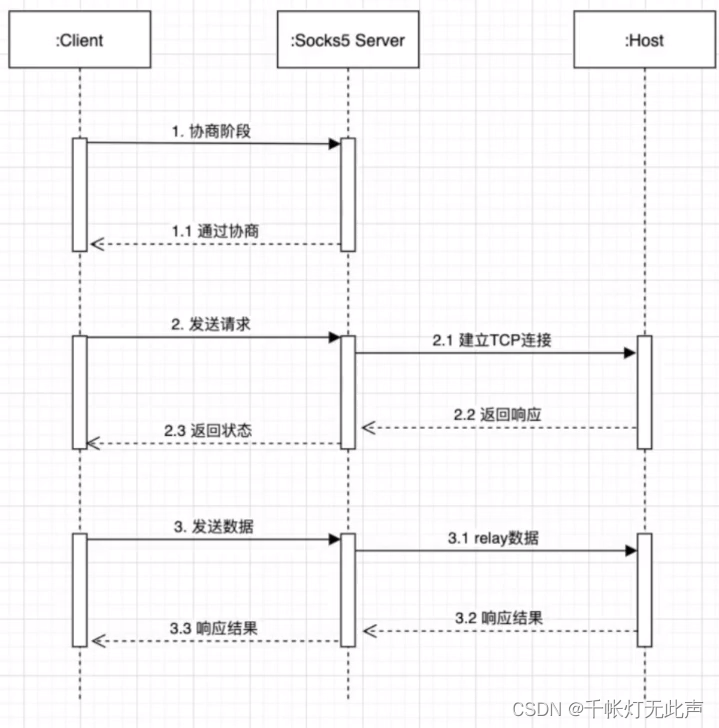
Go语法入门 + 项目实战
👂 Take me Hand Acoustic - Ccile Corbel - 单曲 - 网易云音乐 第3个小项目有问题,不能在Windows下跑,懒得去搜Linux上怎么跑了,已经落下进度了.... 目录 😳前言 🍉Go两小时 🔑小项目实战 …...
QT控件通过qss设置子控件的对齐方式、大小自适应等
一些复杂控件,是有子控件的,每个子控件,都可以通过qss的双冒号选择器来选中,进行独特的样式定义。很多控件都有子控件,太多了,后面单独写一篇文章来介绍各个控件的子控件。这里就随便来几个例子 例如下拉列…...

基于java在线收银系统设计与实现
摘要 科技的力量总是在关键的地方改变着人们的生活,不仅如此,我们的生活也是离不开这样或者那样的科技改变,有的消费者没有时间去商场购物,那么电商和快递的结合让端口到消费者的距离不再遥远;有的房客因地域或者工作的…...
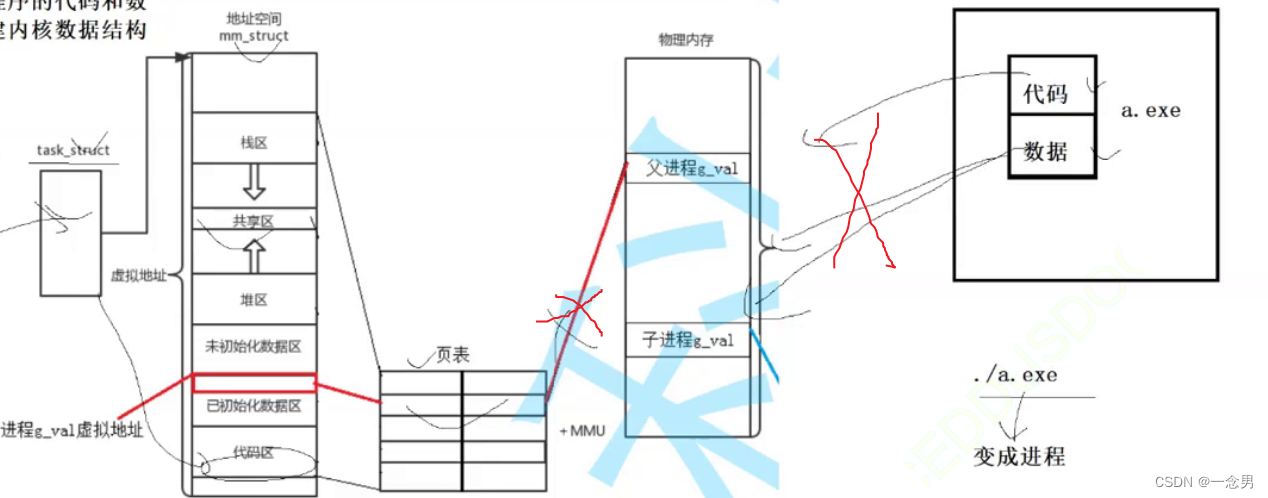
Linux--进程的新建状态
新建状态: 操作系统创建了进程的内核数据结构(task_struct、mm_struct、页表),但是页表没有创建映射关系,而且磁盘里的程序的代码和数据未加载到物理内存...

区间dp,合并石子模板题
设有 N 堆石子排成一排,其编号为 1,2,3,…,N。 每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。 每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的…...

C++代码格式化工具clang-format详细介绍
文章目录 clang-format思考代码风格指南生成您的配置运行 clang-format禁用一段代码的格式设置clang-format的设置预览 clang-format 我曾在许多编程团队工作过,这些团队名义上都有“编程风格指南”。该指南经常被写下来并放置在开发人员很少查看的地方。几乎在每种…...
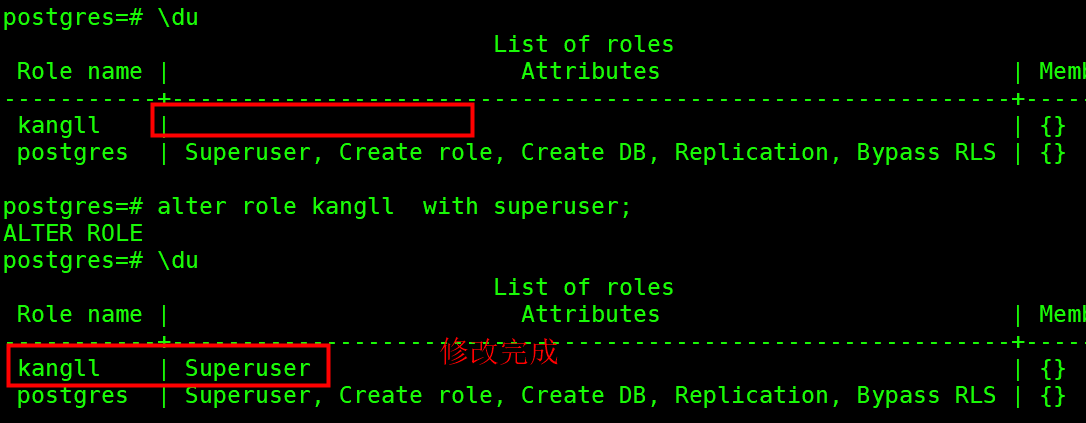
CentOS 7安装PostgreSQL 15版本数据库
目录 一、何为PostgreSQL? 二、PostgreSQL安装 2.1安装依赖 2.2 执行安装 2.3 数据库初始化 2.4 配置环境变量 2.5 创建数据库 2.6 配置远程 2.7 测试远程 三、常用命令 四、用户创建和数据库权限 一、何为PostgreSQL? PostgreSQL是以加州大学…...

QGraphicsView实现简易地图2『瓦片经纬度』
前文链接:QGraphicsView实现简易地图1『加载离线瓦片地图』 地图采用GCJ02 Web 墨卡托投影,最小坐标:(-180.00000000000000,-85.05112877980655),最大坐标:(180.00000000000000,85.05112877980655)。瓦片地图单张图片像…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...

CentOS 7.9安装Nginx1.24.0时报 checking for LuaJIT 2.x ... not found
Nginx1.24编译时,报LuaJIT2.x错误, configuring additional modules adding module in /www/server/nginx/src/ngx_devel_kit ngx_devel_kit was configured adding module in /www/server/nginx/src/lua_nginx_module checking for LuaJIT 2.x ... not…...
