区间dp,合并石子模板题
设有 N 堆石子排成一排,其编号为 1,2,3,…,N。
每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。
每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻,合并时由于选择的顺序不同,合并的总代价也不相同。
例如有 44 堆石子分别为 1 3 5 2, 我们可以先合并 1、2堆,代价为 44,得到 4 5 2, 又合并 1、2堆,代价为 9,得到 9 2 ,再合并得到 11,总代价为 4+9+11=24;
如果第二步是先合并 2、3堆,则代价为 7,得到 4 7,最后一次合并代价为 11,总代价为 4+7+11=22
问题是:找出一种合理的方法,使总的代价最小,输出最小代价。
输入格式
第一行一个数 N 表示石子的堆数 N。
第二行 N 个数,表示每堆石子的质量(均不超过 1000)。
输出格式
输出一个整数,表示最小代价。
数据范围
1≤N≤300
输入样例:
4
1 3 5 2
输出样例:
22#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
const int N = 300 + 5;
const int INF = 1e9;
int n;
int sum[N], dp[N][N];int main() {cin >> n;for (int i = 1; i <= n; i++) {scanf("%d", &sum[i]);sum[i] += sum[i - 1];}for (int len = 2; len <= n; len++) {for (int l = 1; l + len - 1 <= n; l++) {int r = len + l - 1;dp[l][r] = INF;for (int k = l; k < r; k++) {dp[l][r] = min(dp[l][r], dp[l][k] + dp[k + 1][r] + sum[r] - sum[l - 1]);}}}cout << dp[1][n] << endl;return 0;
}
代码2
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
using namespace std;
typedef long long LL;
const int N = 300 + 5;
const int INF = 1e9;
int n;
LL sum[N], dp[N][N];int main() {cin >> n;for (int i = 1; i <= n; i++) {scanf("%ld", &sum[i]);sum[i] += sum[i - 1];}for (int i = n; i >= 1; i--) {for (int j = i + 1; j <= n; j++) {dp[i][j] = INF;for (int k = i; k < j; k++) {dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + sum[j] - sum[i - 1]);}}}cout << dp[1][n] << endl;return 0;
}
相关文章:

区间dp,合并石子模板题
设有 N 堆石子排成一排,其编号为 1,2,3,…,N。 每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。 每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的…...

C++代码格式化工具clang-format详细介绍
文章目录 clang-format思考代码风格指南生成您的配置运行 clang-format禁用一段代码的格式设置clang-format的设置预览 clang-format 我曾在许多编程团队工作过,这些团队名义上都有“编程风格指南”。该指南经常被写下来并放置在开发人员很少查看的地方。几乎在每种…...
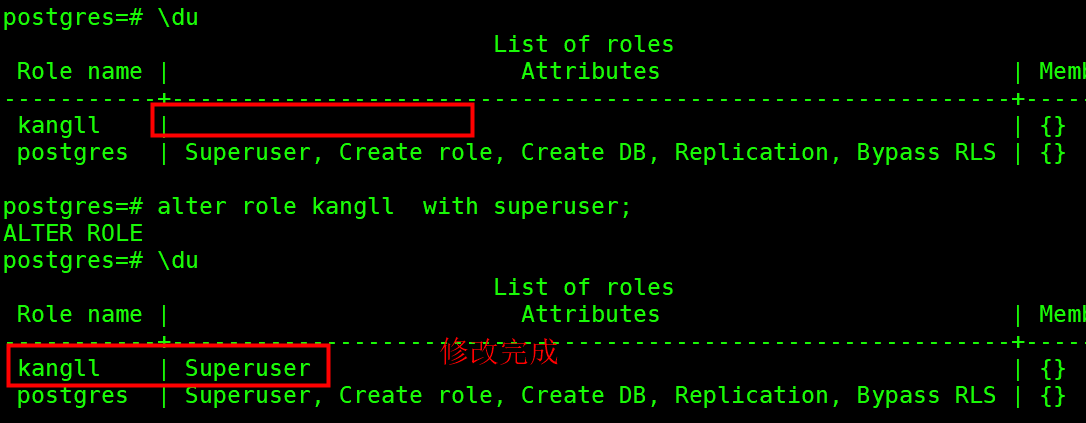
CentOS 7安装PostgreSQL 15版本数据库
目录 一、何为PostgreSQL? 二、PostgreSQL安装 2.1安装依赖 2.2 执行安装 2.3 数据库初始化 2.4 配置环境变量 2.5 创建数据库 2.6 配置远程 2.7 测试远程 三、常用命令 四、用户创建和数据库权限 一、何为PostgreSQL? PostgreSQL是以加州大学…...

QGraphicsView实现简易地图2『瓦片经纬度』
前文链接:QGraphicsView实现简易地图1『加载离线瓦片地图』 地图采用GCJ02 Web 墨卡托投影,最小坐标:(-180.00000000000000,-85.05112877980655),最大坐标:(180.00000000000000,85.05112877980655)。瓦片地图单张图片像…...

医学图像重建—第一章笔记
序言 本书涵盖内容: 2D parallel beam imaging 2D fan beam imaging 3D parallel ray imaging 3D parallel plane imaging 3D cone beam imaging 算法包括:analytical method,iterative method 应用于: X-ray CT single photon…...

python-pytorch基础之神经网络分类
这里写目录标题 生成数据函数定义数据集定义loader加载数据定义神经网络模型测试输出是否为2个输入数据,输出结果 训练模型函数计算正确率 训练数据并保存模型测试模型准备数据加载模型预测对比结果 生成数据函数 import randomdef get_rectangle():widthrandom.ra…...
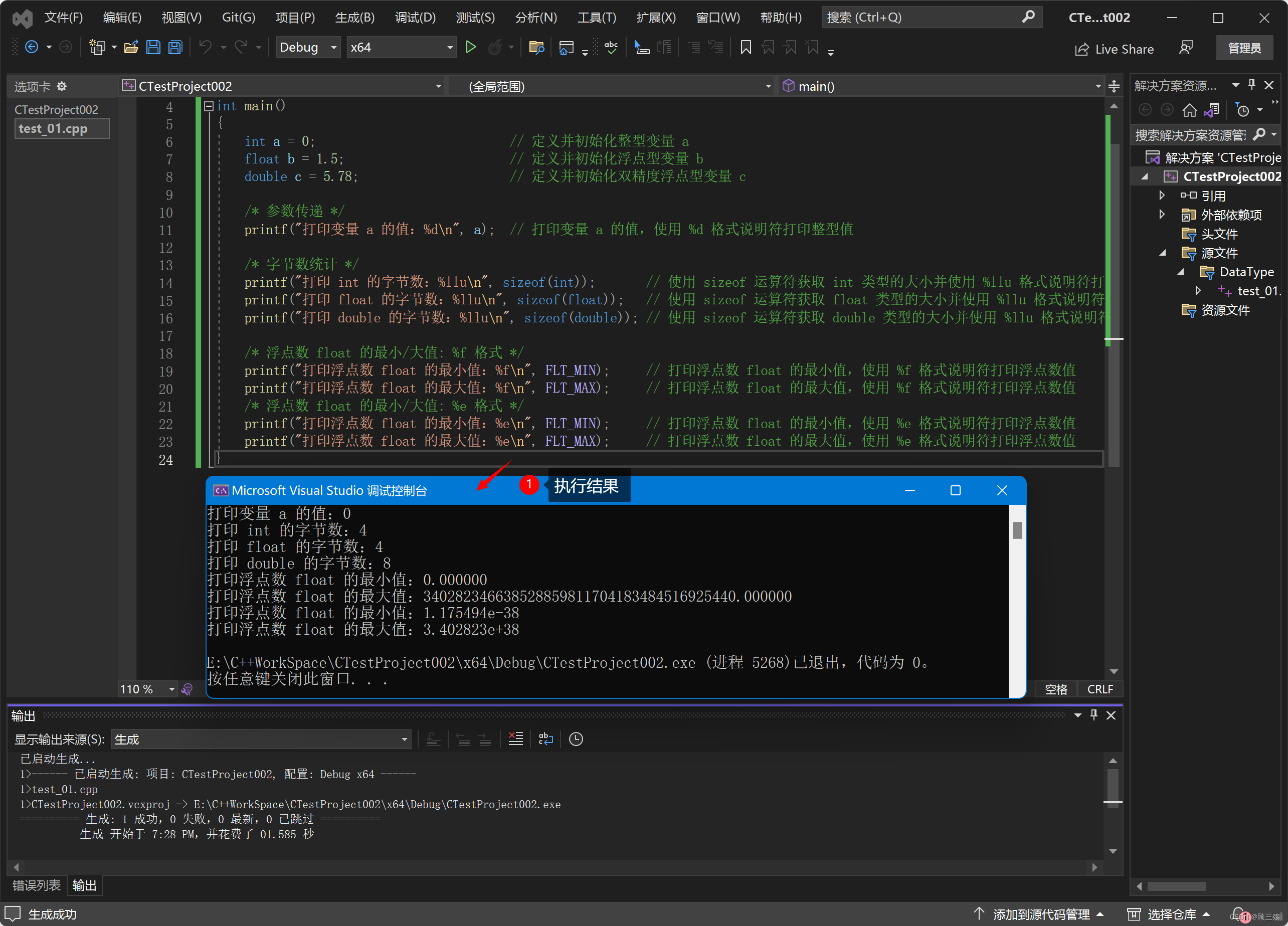
【C++ 程序设计】实战:C++ 变量实践练习题
目录 01. 变量:定义 02. 变量:初始化 03. 变量:参数传递 04. 变量:格式说明符 ① 占位符 “%d” 改为格式说明符 “%llu” ② 占位符 “%d” 改为格式说明符 “%f” 或 “%e” 05. 变量:字节数统计 06. 变量&a…...
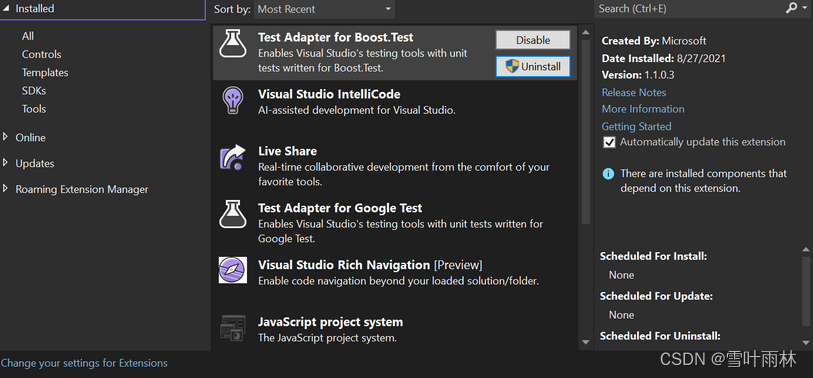
微软对Visual Studio 17.7 Preview 4进行版本更新,新插件管理器亮相
近期微软发布了Visual Studio 17.7 Preview 4版本,而在这个版本当中,全新设计的扩展插件管理器将亮相,并且可以让用户可更简单地安装和管理扩展插件。 据了解,目前用户可以从 Visual Studio Marketplace 下载各式各样的 VS 扩展插…...
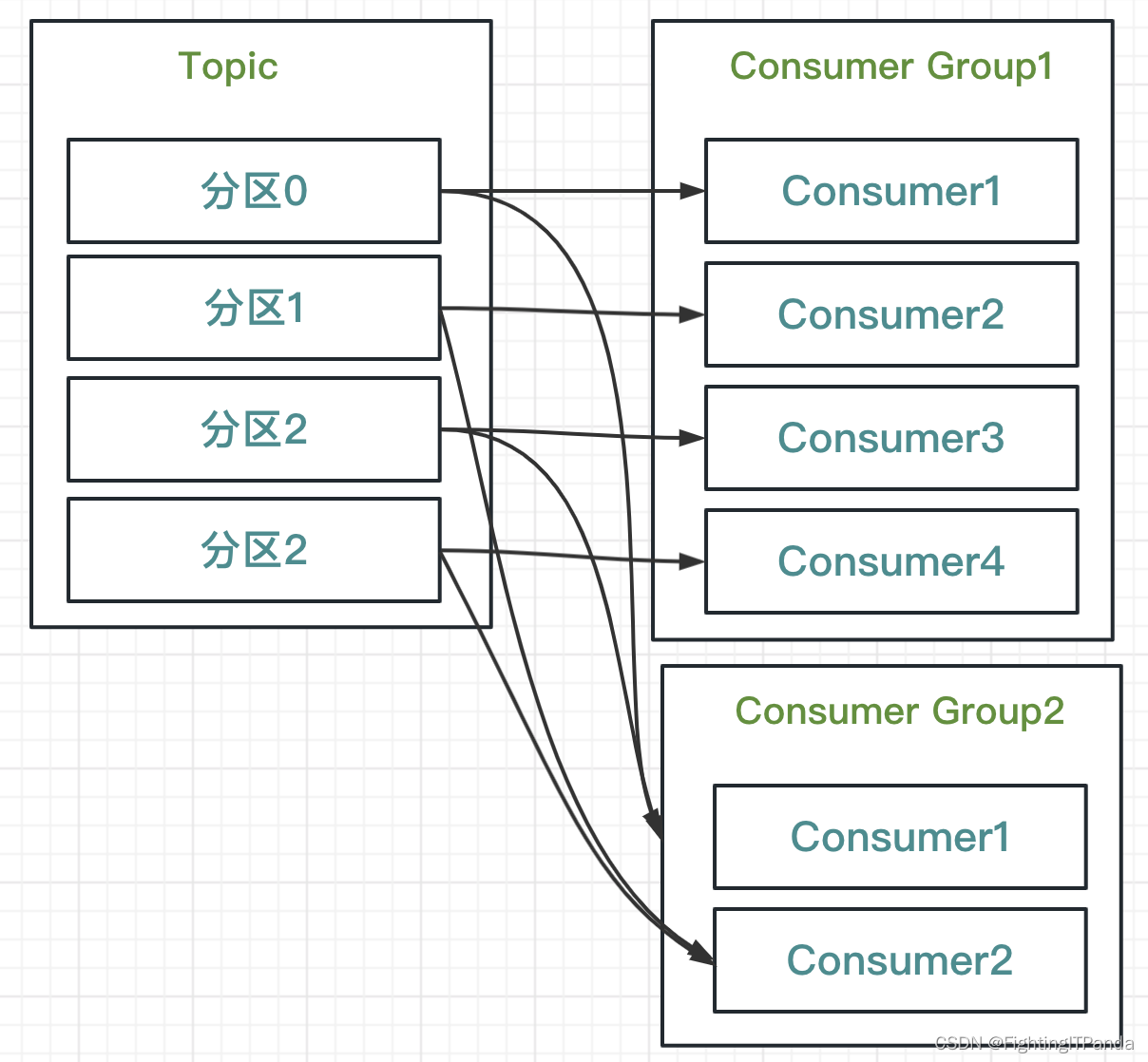
Kafka 入门到起飞 - Kafka怎么做到保障消息不会重复消费的? 消费者组是什么?
Kafka怎么做到避免消息重复消费的? 消费者组是什么? 消费者: 1、订阅Topic(主题) 2、从订阅的Topic消费(pull)消息, 3、将消费消息的offset(偏移量)保存在K…...

MongoDB 的增、查、改、删
Monogo使用 增 单条增加 db.member.insertOne({"name":"张三","age":18,"create":new Date()}) db.member.insert({"name":"李四1","age":18,"create":new Date()}) db.member.insertOne(…...

mysql常用操作命令
mysql常用操作命令 mysql:单进程多线程模型,一个SQL语句无法利用多个cpu core 一:基本命令 0.查看当前连接数 show global status like Thread$; show variables like "%timeout%"; show variables like "log_%";1.查看当前连接状态 show processlist…...

数学建模常见模型汇总
优化问题 线性规划、半定规划、几何规划、非线性规划、整数规划、多目标规划(分层序列法)、动态规划、存贮论、代理模型、响应面分析法、列生成算法 预测模型 微分方程、小波分析、回归分析、灰色预测、马尔可夫预测、时间序列分析(AR MAMA.RMA ARTMA LSTM神经网络)、混沌模…...
)
C#使用LINQ查询操作符实例代码(二)
目录 六、连表操作符 1、内连接2、左外连接(DefaultIfEmpty)3、组连接七、集合操作 八、分区操作符 1、Take():2、TakeWhile():3、Skip():4、SkipWhile():九、聚合操作符 1、Count: 返回集合项数。 2、LongCount&…...

jenkinsfile小试牛刀
序 本文主要演示一下如何用jenkinsfile来编译java服务 安装jenkins 这里使用docker来安装jenkins docker run --name jenkins-docker \ --volume $HOME/jenkins_home:/var/jenkins_home \ -p 8080:8080 jenkins/jenkins:2.416之后访问http://${yourip}:8080,然后…...

C++ xmake构建
文章目录 一、xmake.lua二、xmake常用语句 一、xmake.lua --xmake.luaset_project("XXX")add_rules("mode.debug", "mode.release") set_config("arch", "x64")if is_plat("windows") then -- the release modei…...
推荐带500创作模型的付费创作V2.1.0独立版系统源码
ChatGPT 付费创作系统 V2.1.0 提供最新的对应版本小程序端,上一版本增加了 PC 端绘画功能, 绘画功能采用其他绘画接口 – 意间 AI,本版新增了百度文心一言接口。 后台一些小细节的优化及一些小 BUG 的处理,前端进行了些小细节优…...
wps图表怎么改横纵坐标,MLP 多层感知器和CNN卷积神经网络区别
目录 wps表格横纵坐标轴怎么设置? MLP (Multilayer Perceptron) 多层感知器 CNN (Convolutional Neural Network) 卷积神经网络 多层感知器MLP,全连接网络,DNN三者的关系 wps表格横纵坐标轴怎么设置? 1、打开表格点击图的右侧…...

rdb和aof
RDB持久化:原理是将Redis在内存中的数据库记录定时dump到磁盘上的RDB持久化AOF持久化:原理是将Redis的操作日志以追加的方式写入文件 rdb: 开启方式:客户端可以通过向Redis服务器发送save或bgsave命令让服务器生成rdb文件&#…...
TCP网络通信编程之网络上传文件
【图片】 【思路解析】 【客户端代码】 import java.io.*; import java.net.InetAddress; import java.net.Socket; import java.net.UnknownHostException;/*** ProjectName: Study* FileName: TCPFileUploadClient* author:HWJ* Data: 2023/7/29 18:44*/ public class TCPFil…...

Java中对Redis的常用操作
目录 数据类型五种常用数据类型介绍各种数据类型特点 常用命令字符串操作命令哈希操作命令列表操作命令集合操作命令有序集合操作命令通用命令 在Java中操作RedisRedis的Java客户端Spring Data Redis使用方式介绍环境搭建配置Redis数据源编写配置类,创建RedisTempla…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
