Merge the squares! 2023牛客暑期多校训练营4-H
登录—专业IT笔试面试备考平台_牛客网
题目大意:有n*n个边长为1的小正方形摆放在边长为n的大正方形中,每次可以选择不超过50个正方形,将其合并为一个更大的正方形,求一种可行的操作使所有小正方形都被合并成一个n*n的大正方形
1<=n<=1000
思路:对于一个a*b(a>b)的矩形,我们可以用类似黄金分割的办法将其分割成cnt个b*b的正方形,然后剩下一个(a-cnt)*b*b的矩形,继续分割,一定能最后分割到剩下的矩形边长为1的情况,所以我们将一开始的大正方形分割成左上、右下两个边长分别为a,b的正方形,和剩下两个a*b的矩形,就可以完成题目要求。
现在来求a,b,我们可以从1到n枚举分割出来的矩形边长a,b=n-a,然后用辗转相减法,求出最后剩下边长为1的矩形是,一共构造出了几个正方形,如果<=24,那么两个矩形加起来加上a*a,b*b的正方形就不会超过50个
打表求出每个正方形的边长对应的a,b之后,我们就可以递归求解,每次从大正方形开始,先记录答案,然后分别递归到四个分出来的图形中,横着的和竖着的也就是一开始左下和右上的矩形要分别写一个递归,最后将所有答案逆序输出即可
//#include<__msvc_all_public_headers.hpp>
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
typedef long long ll;
const ll MOD=998244353;
int siz[N];
vector<pair<int, pair<int, int>>>ans;
bool check(int a, int b)
{//辗转相减法计算a*b的矩形能分割出几个正方形if (!b)return a <= 7;//7*7以下的可以直接合并成一个int cnt = 1;while (b){cnt += a / b;int c = a % b;a = b;b = c;}return cnt <= 25;//将初始的大正方形分割成了两个矩形
}
void dfs2(int x, int y, int leny, int lenx);
void dfs3(int x, int y, int leny, int lenx);
void dfs(int x, int y, int s)
{//当前正方形的坐标,大小if (s == 1)return;//边长为1的不用记录ans.push_back({ x,{y,s} });if (!siz[s])return;//分不了的就和别人一起合并即可int a = s - siz[s], b = siz[s];dfs2(x + a, y, b, a);//左下角的矩形dfs3(x, y + a, a, b);//右上角的矩形dfs(x, y, a);//左上角的正方形dfs(x + a, y + a, b);//右下角的正方形
}
void dfs2(int x, int y, int lenx, int leny)
{//矩形坐标,纵轴长,横轴长if (lenx <= 1)return;int cnt = leny / lenx;//当前矩形能分出几个正方形for (int i = 0; i < cnt; i++){dfs(x, y + i * lenx, lenx);//继续分割切出来的每个小正方形}dfs3(x, y + cnt * lenx, lenx, leny % lenx);//剩下的矩形变成了竖着的
}
void dfs3(int x, int y, int lenx, int leny)
{//横着的矩形if (leny <= 1)return;int cnt = lenx / leny;for (int i = 0; i < cnt; i++){dfs(x + i * leny, y, leny);}dfs2(x + cnt * leny, y, lenx % leny, leny);
}
int main()
{int n;cin >> n;for (int i = 1; i <= n; i++){for (int j = 0; j <= i / 2; j++){//检查n以内所有分割方案是否合法if (check(i - j, j)){siz[i] = j;break;}}}dfs(1, 1, n);cout << ans.size() << endl;reverse(ans.begin(), ans.end());//获取的答案是从大到小,要求是从小到大for (int i = 0; i < ans.size(); i++){cout << ans[i].first << " " << ans[i].second.first << " " << ans[i].second.second << endl;}return 0;
}相关文章:

Merge the squares! 2023牛客暑期多校训练营4-H
登录—专业IT笔试面试备考平台_牛客网 题目大意:有n*n个边长为1的小正方形摆放在边长为n的大正方形中,每次可以选择不超过50个正方形,将其合并为一个更大的正方形,求一种可行的操作使所有小正方形都被合并成一个n*n的大正方形 1…...
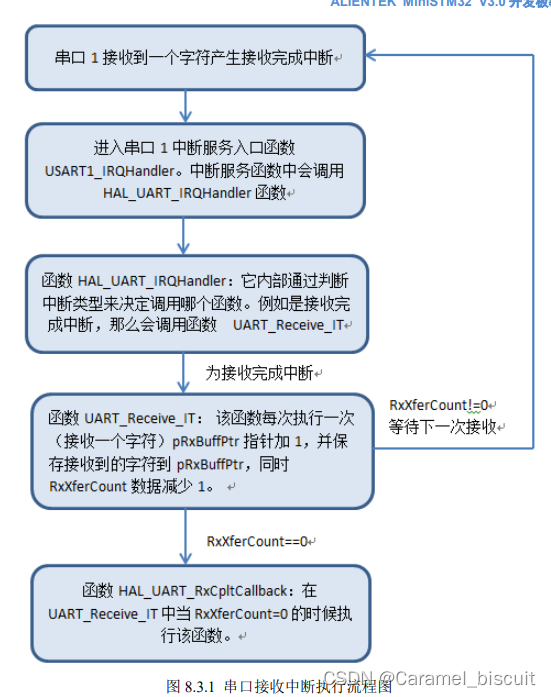
STM32 串口学习(二)
要用跳线帽将PA9与RXD相连,PA10与TXD相连。 软件设计 void uart_init(u32 baud) {//UART 初始化设置UART1_Handler.InstanceUSART1; //USART1UART1_Handler.Init.BaudRatebound; //波特率UART1_Handler.Init.WordLengthUART_WORDLENGTH_8B; //字长为 8 位数据格式U…...
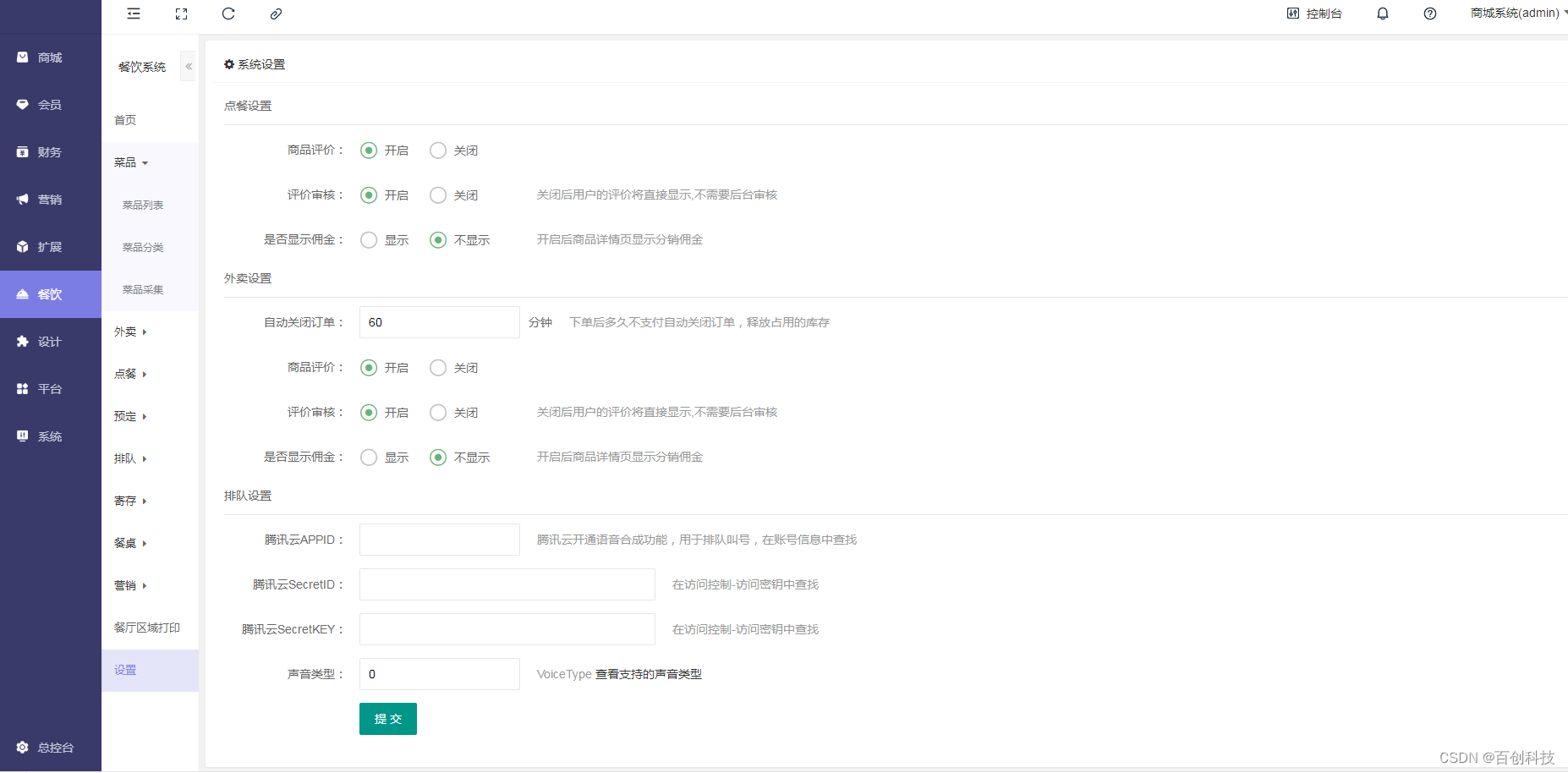
点大商城V2_2.5.0 全开源版 商家自营+多商户入驻 百度+支付宝+QQ+头条+小程序端+unipp开源前端安装测试教程
安装测试环境:Nginx 1.20PHP7.2MySQL 5.6 修复了无法上传开放平台问题 安装说明: 1、上传后端目录至网站 2、导入提供的数据库文件 3、修改数据库配置文件根目录下config.php,增加数据库用户名和密码 4、网站后台直接访问网址ÿ…...

“深入理解SpringBoot:从入门到精通“
标题:深入理解Spring Boot:从入门到精通 摘要:本文将介绍Spring Boot的基本概念和核心特性,并通过示例代码演示如何使用Spring Boot构建一个简单的Web应用程序。 1. 简介 Spring Boot是一个开源的Java框架,旨在简化基…...

PCB绘制时踩的坑 - SOT-223封装
SOT-223封装并不是同一的,细分的话可以分为两种常用的封装。尤其是tab脚的属性很容易搞错。如果你想着用tab脚连接有属性的铺铜,来提高散热效率,那么你一定要注意你购买的器件tab脚的属性。 第一种如下图,第1脚为GND,第…...
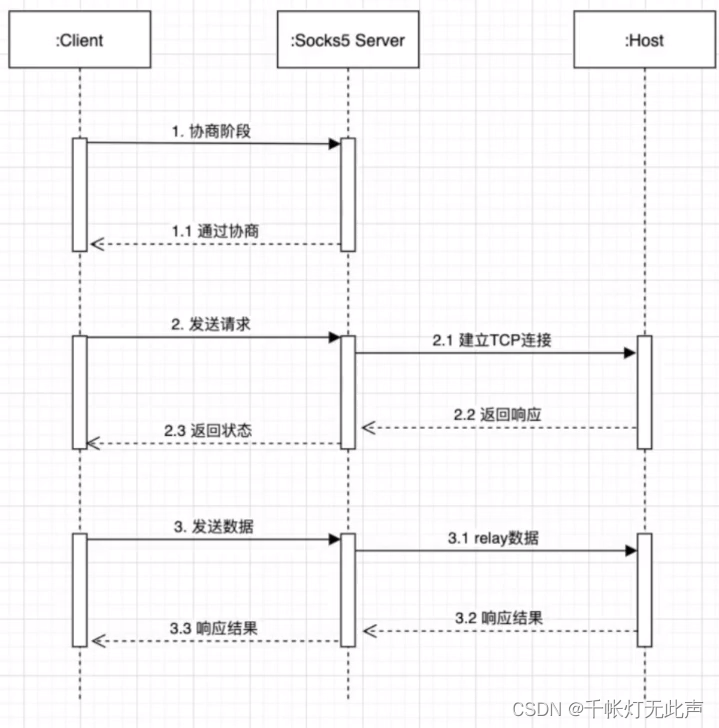
Go语法入门 + 项目实战
👂 Take me Hand Acoustic - Ccile Corbel - 单曲 - 网易云音乐 第3个小项目有问题,不能在Windows下跑,懒得去搜Linux上怎么跑了,已经落下进度了.... 目录 😳前言 🍉Go两小时 🔑小项目实战 …...
QT控件通过qss设置子控件的对齐方式、大小自适应等
一些复杂控件,是有子控件的,每个子控件,都可以通过qss的双冒号选择器来选中,进行独特的样式定义。很多控件都有子控件,太多了,后面单独写一篇文章来介绍各个控件的子控件。这里就随便来几个例子 例如下拉列…...

基于java在线收银系统设计与实现
摘要 科技的力量总是在关键的地方改变着人们的生活,不仅如此,我们的生活也是离不开这样或者那样的科技改变,有的消费者没有时间去商场购物,那么电商和快递的结合让端口到消费者的距离不再遥远;有的房客因地域或者工作的…...
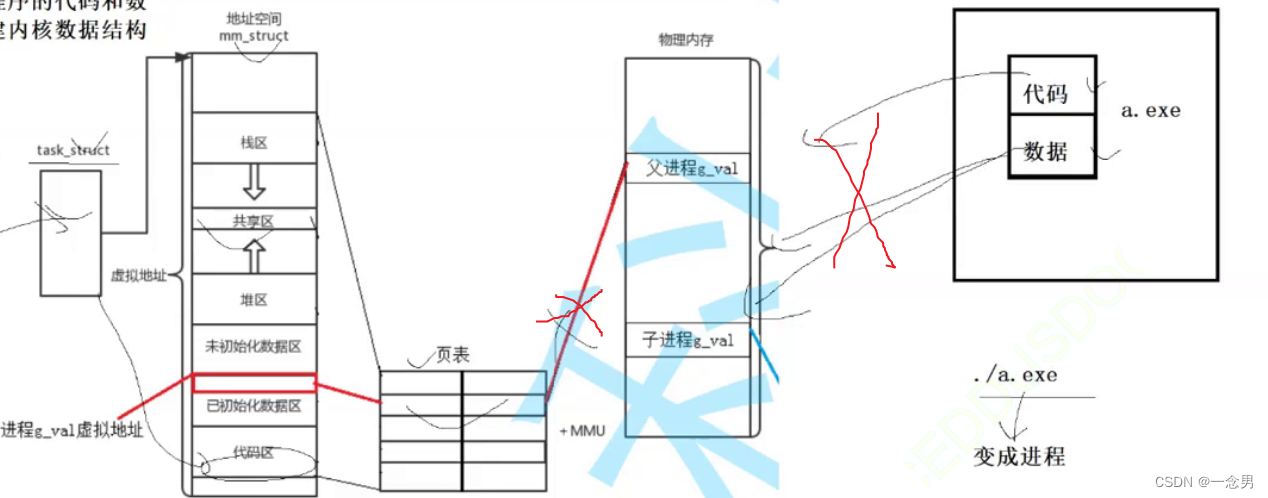
Linux--进程的新建状态
新建状态: 操作系统创建了进程的内核数据结构(task_struct、mm_struct、页表),但是页表没有创建映射关系,而且磁盘里的程序的代码和数据未加载到物理内存...

区间dp,合并石子模板题
设有 N 堆石子排成一排,其编号为 1,2,3,…,N。 每堆石子有一定的质量,可以用一个整数来描述,现在要将这 N 堆石子合并成为一堆。 每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的…...

C++代码格式化工具clang-format详细介绍
文章目录 clang-format思考代码风格指南生成您的配置运行 clang-format禁用一段代码的格式设置clang-format的设置预览 clang-format 我曾在许多编程团队工作过,这些团队名义上都有“编程风格指南”。该指南经常被写下来并放置在开发人员很少查看的地方。几乎在每种…...
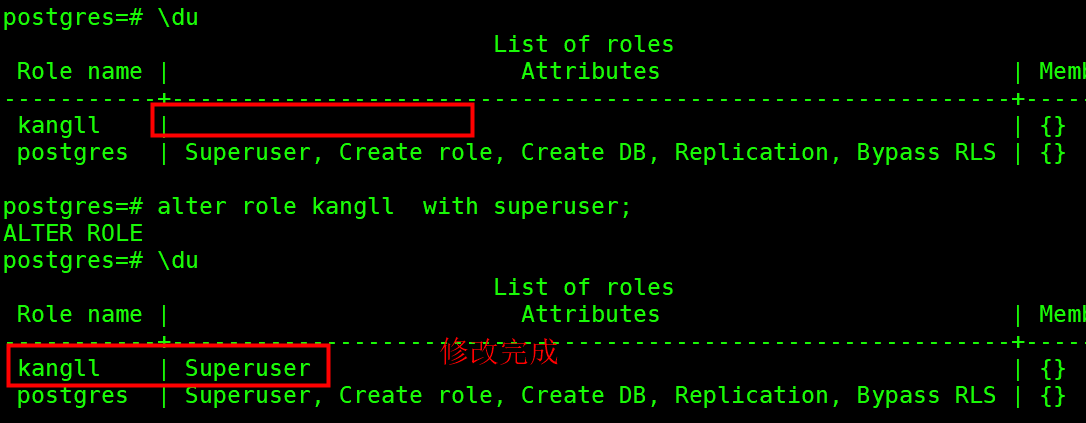
CentOS 7安装PostgreSQL 15版本数据库
目录 一、何为PostgreSQL? 二、PostgreSQL安装 2.1安装依赖 2.2 执行安装 2.3 数据库初始化 2.4 配置环境变量 2.5 创建数据库 2.6 配置远程 2.7 测试远程 三、常用命令 四、用户创建和数据库权限 一、何为PostgreSQL? PostgreSQL是以加州大学…...

QGraphicsView实现简易地图2『瓦片经纬度』
前文链接:QGraphicsView实现简易地图1『加载离线瓦片地图』 地图采用GCJ02 Web 墨卡托投影,最小坐标:(-180.00000000000000,-85.05112877980655),最大坐标:(180.00000000000000,85.05112877980655)。瓦片地图单张图片像…...

医学图像重建—第一章笔记
序言 本书涵盖内容: 2D parallel beam imaging 2D fan beam imaging 3D parallel ray imaging 3D parallel plane imaging 3D cone beam imaging 算法包括:analytical method,iterative method 应用于: X-ray CT single photon…...

python-pytorch基础之神经网络分类
这里写目录标题 生成数据函数定义数据集定义loader加载数据定义神经网络模型测试输出是否为2个输入数据,输出结果 训练模型函数计算正确率 训练数据并保存模型测试模型准备数据加载模型预测对比结果 生成数据函数 import randomdef get_rectangle():widthrandom.ra…...
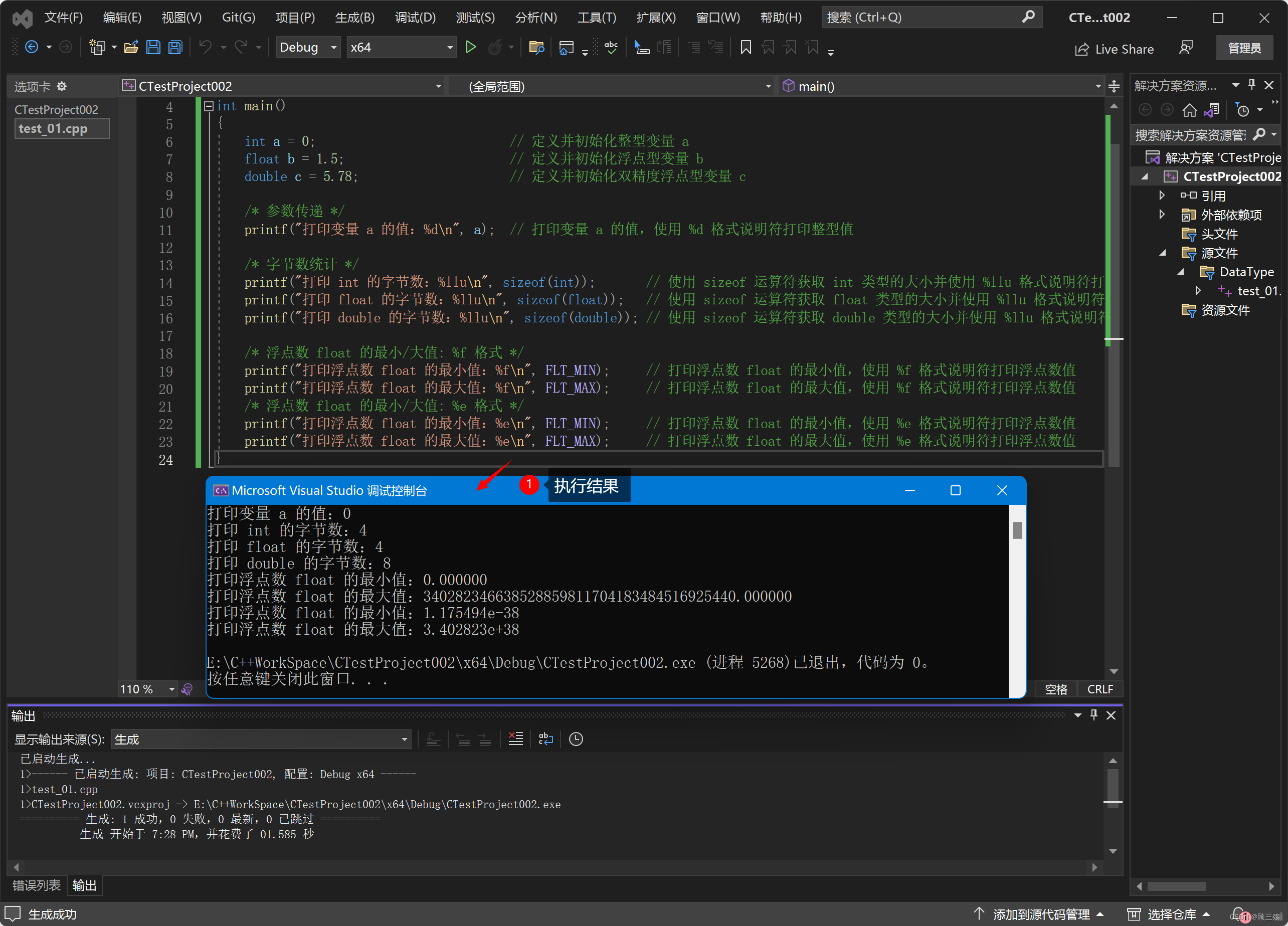
【C++ 程序设计】实战:C++ 变量实践练习题
目录 01. 变量:定义 02. 变量:初始化 03. 变量:参数传递 04. 变量:格式说明符 ① 占位符 “%d” 改为格式说明符 “%llu” ② 占位符 “%d” 改为格式说明符 “%f” 或 “%e” 05. 变量:字节数统计 06. 变量&a…...
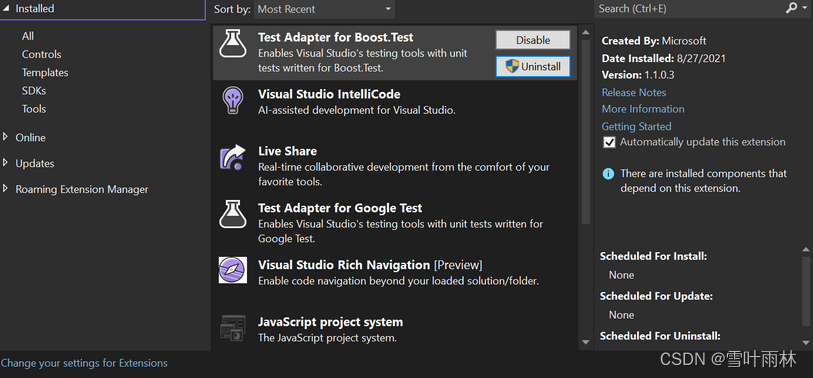
微软对Visual Studio 17.7 Preview 4进行版本更新,新插件管理器亮相
近期微软发布了Visual Studio 17.7 Preview 4版本,而在这个版本当中,全新设计的扩展插件管理器将亮相,并且可以让用户可更简单地安装和管理扩展插件。 据了解,目前用户可以从 Visual Studio Marketplace 下载各式各样的 VS 扩展插…...
Kafka 入门到起飞 - Kafka怎么做到保障消息不会重复消费的? 消费者组是什么?
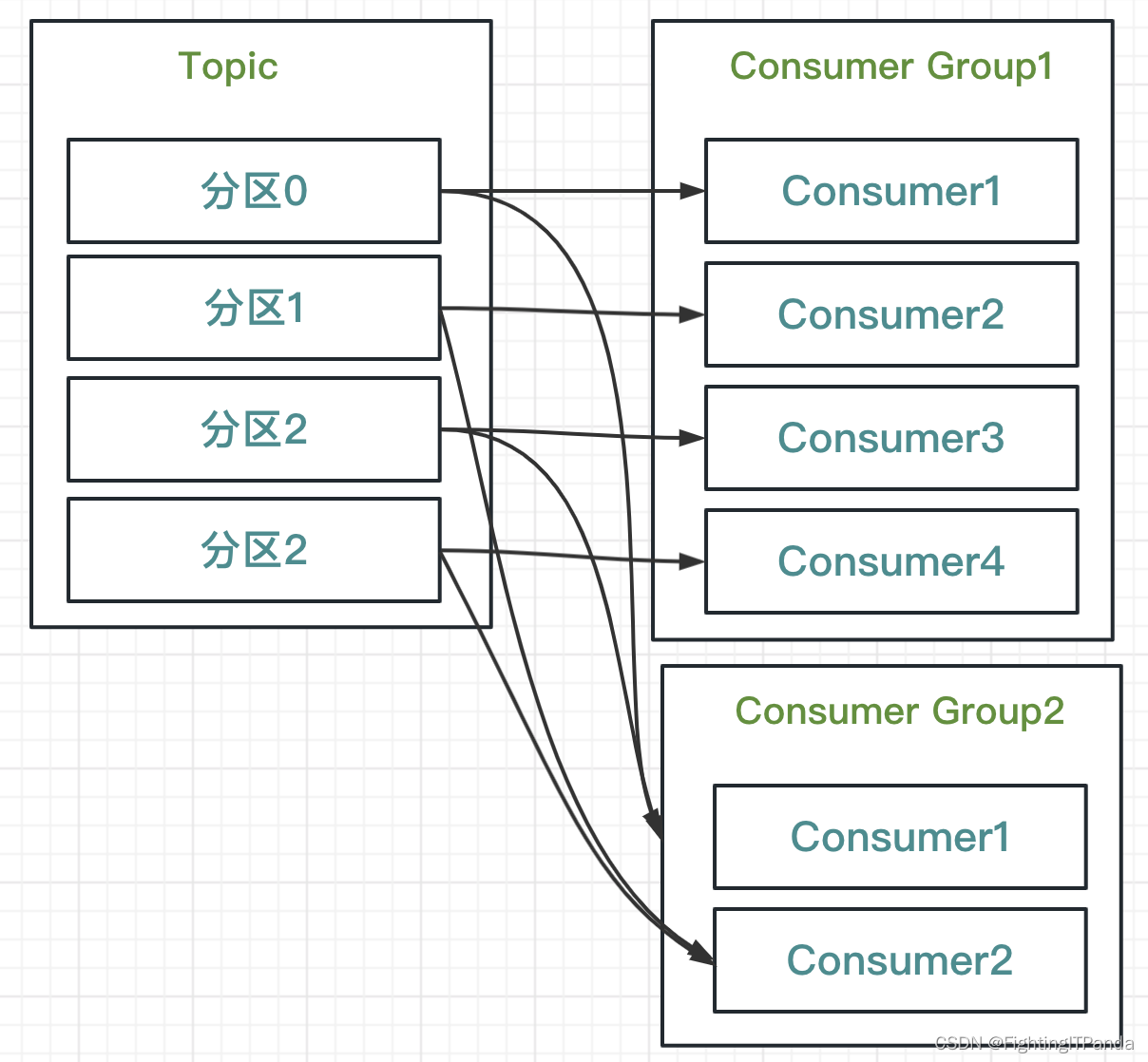
Kafka怎么做到避免消息重复消费的? 消费者组是什么? 消费者: 1、订阅Topic(主题) 2、从订阅的Topic消费(pull)消息, 3、将消费消息的offset(偏移量)保存在K…...

MongoDB 的增、查、改、删
Monogo使用 增 单条增加 db.member.insertOne({"name":"张三","age":18,"create":new Date()}) db.member.insert({"name":"李四1","age":18,"create":new Date()}) db.member.insertOne(…...

mysql常用操作命令
mysql常用操作命令 mysql:单进程多线程模型,一个SQL语句无法利用多个cpu core 一:基本命令 0.查看当前连接数 show global status like Thread$; show variables like "%timeout%"; show variables like "log_%";1.查看当前连接状态 show processlist…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
