机器学习笔记之优化算法(四)线搜索方法(步长角度;非精确搜索)
机器学习笔记之优化算法——线搜索方法[步长角度,非精确搜索]
- 引言
- 回顾:精确搜索步长及其弊端
- 非精确搜索近似求解最优步长的条件
- 反例论述
引言
上一节介绍了从精确搜索的步长角度观察了线搜索方法,本节将从非精确搜索的步长角度重新观察线搜索方法。
回顾:精确搜索步长及其弊端
关于线搜索方法的迭代过程表示如下:
x k + 1 = x k + α k ⋅ P k x_{k+1} = x_k + \alpha_k \cdot \mathcal P_k xk+1=xk+αk⋅Pk
其中:
- 变量 x k , x k + 1 ∈ { x k } k = 0 ∞ x_k,x_{k+1} \in \{x_{k}\}_{k=0}^{\infty} xk,xk+1∈{xk}k=0∞表示先搜索处理优化问题时,迭代过程中产生的数值解;
- α k \alpha_{k} αk是一个标量,表示步长信息;
- P k \mathcal P_k Pk可视作一个单位向量,描述当前迭代步骤下数值解更新的方向信息。
如果P k \mathcal P_k Pk是一个描述方向的常规向量,依然可以将其表示为”系数× \times ×单位向量“的形式,最后将系数与α k \alpha_k αk合并即可。
而基于精确搜索线搜索方法寻找最优步长的基本逻辑是:
- 固定住单位向量 P k \mathcal P_k Pk,此时关于当前时刻数值解对应的目标函数 f ( x k + 1 ) f(x_{k+1}) f(xk+1)可看作是仅与步长变量 α \alpha α相关的一个函数 ϕ ( α ) \phi(\alpha) ϕ(α):
f ( x k + 1 ) = f ( x k + α ⋅ P k ) ≜ ϕ ( α ) \begin{aligned} f(x_{k+1}) = f(x_k + \alpha \cdot \mathcal P_k) \triangleq \phi(\alpha) \end{aligned} f(xk+1)=f(xk+α⋅Pk)≜ϕ(α) - 通过选择合适步长 α k \alpha_k αk,使得目标函数 f ( x k + 1 ) f(x_{k+1}) f(xk+1)达到最小,从而达到当前迭代步骤优化程度最大的目的:
α k = arg min α > 0 f ( x k + 1 ) \alpha_k = \mathop{\arg\min}\limits_{\alpha > 0} f(x_{k+1}) αk=α>0argminf(xk+1)
具体步骤表示如下:
对每个迭代步骤 k = 1 , 2 , ⋯ , ∞ k=1,2,\cdots,\infty k=1,2,⋯,∞执行如下操作:
由于此时 f ( x k + 1 ) = ϕ ( α ) f(x_{k+1}) = \phi(\alpha) f(xk+1)=ϕ(α)仅包含 α \alpha α一个变量,因而仅需要对 ϕ ( α ) \phi(\alpha) ϕ(α)求导,然后从极值中选出最小值即可。
- 关于 ϕ ( α ) \phi(\alpha) ϕ(α)对 α \alpha α进行求导操作:
∂ ϕ ( α ) ∂ α = [ ∇ f ( x k + α ⋅ P k ) ] T ⋅ P k \frac{\partial \phi(\alpha)}{\partial \alpha} = \left[\nabla f(x_k + \alpha \cdot \mathcal P_k)\right]^T \cdot \mathcal P_k ∂α∂ϕ(α)=[∇f(xk+α⋅Pk)]T⋅Pk - 令 ∂ ϕ ( α ) ∂ α ≜ 0 \begin{aligned}\frac{\partial \phi(\alpha)}{\partial \alpha} \triangleq 0\end{aligned} ∂α∂ϕ(α)≜0,从而求解位于极值点的 α \alpha α信息,再选择使 f ( x k + 1 ) f(x_{k+1}) f(xk+1)最小对应的 α \alpha α即可,示例图像表示如下:
这仅仅是关于ϕ ( α ) \phi(\alpha) ϕ(α)的一种描述。由于我们对目标函数f ( ⋅ ) f(\cdot) f(⋅)未知,我们不能得到ϕ ( α ) \phi(\alpha) ϕ(α)精确的函数图像。唯一知道ϕ ( 0 ) = f ( x k ) \phi(0) = f(x_k) ϕ(0)=f(xk)(无法取到)且∂ ϕ ( α ) ∂ α ∣ α = 0 < 0 \begin{aligned}\frac{\partial \phi(\alpha)}{\partial \alpha} |_{\alpha=0} < 0\end{aligned} ∂α∂ϕ(α)∣α=0<0,详细过程见上一节。

貌似上述流程看起来并不复杂,但在真实环境下,精确搜索参与的迭代过程可能是麻烦的:
- 首先,对于目标函数 f ( ⋅ ) f(\cdot) f(⋅)的复杂程度我们一无所知。真实环境中, f ( ⋅ ) f(\cdot) f(⋅)可能是极复杂的。这意味着: ∂ ϕ ( α ) ∂ α \begin{aligned}\frac{\partial \phi(\alpha)}{\partial \alpha}\end{aligned} ∂α∂ϕ(α)可能极难表达甚至是无法表达;
- 其中求导以及获取极值的操作仅仅是一次迭代过程中的操作。若每一次迭代过程都要执行上述操作,对应的计算代价有可能极高;
- 实际上,精确求解当前迭代步骤的最优步长不是我们关注的重点,我们希望每次迭代过程中,使用较小的计算代价得到一个比较不错的步长结果,从而降低整体计算代价。
很明显,精确搜索的求解过程是一个求解析解的过程。下面我们观察如何通过求解数值解的方式对最优步长的获取过程进行优化。
非精确搜索近似求解最优步长的条件
首先思考:步长变量 α \alpha α需要满足什么条件,才能够使 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞收敛,并最终得到目标函数的最优解 f ∗ f^* f∗:
{ f ( x k ) } k = 0 ∞ ⇒ f ∗ \{f(x_k)\}_{k=0}^{\infty} \Rightarrow f^* {f(xk)}k=0∞⇒f∗
根据我们关于线搜索方法的假设,首先必然需要使 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞服从严格的单调性:
ϕ ( α ) = f ( x k + 1 ) < f ( x k ) = ϕ ( 0 ) k = 0 , 1 , 2 , ⋯ \phi(\alpha) = f(x_{k+1}) < f(x_k) = \phi(0) \quad k=0,1,2,\cdots ϕ(α)=f(xk+1)<f(xk)=ϕ(0)k=0,1,2,⋯
新的思考:如果步长变量 α \alpha α仅仅满足上述条件,是否能够保证 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞最终收敛至最优解 ? ? ?
答案是否定的,并且关于两个事件:
- 事件 1 1 1: ϕ ( α ) = f ( x k + 1 ) < f ( x k ) = ϕ ( 0 ) k = 0 , 1 , 2 , ⋯ \phi(\alpha) = f(x_{k+1}) < f(x_k) = \phi(0) \quad k=0,1,2,\cdots ϕ(α)=f(xk+1)<f(xk)=ϕ(0)k=0,1,2,⋯;
- 事件 2 2 2: { f ( x k ) } k = 0 ∞ ⇒ f ∗ \{f(x_k)\}_{k=0}^{\infty} \Rightarrow f^* {f(xk)}k=0∞⇒f∗
事件 1 1 1是事件 2 2 2的必要不充分条件。也就是说:事件 1 1 1推不出事件 2 2 2,相反,事件 2 2 2能够推出事件 1 1 1。
反例论述
这里描述一个反例:
- 假设真正的目标函数 f ( ⋅ ) f(\cdot) f(⋅)表示如下:

可以看出,该目标函数存在最小值 − 1 -1 −1。而我们的目标是通过求数值解的方式取到 − 1 -1 −1。
- 而这个数值解仅仅受到事件 1 1 1的约束。也就是说:在迭代过程中仅满足 f ( x k + 1 ) < f ( x k ) f(x_{k+1}) < f(x_k) f(xk+1)<f(xk)即可。至此,假设:数值解 { x k } k = 1 ∞ \{x_k\}_{k=1}^{\infty} {xk}k=1∞对应的目标函数结果 { f ( x k ) } k = 1 ∞ \{f(x_k)\}_{k=1}^{\infty} {f(xk)}k=1∞满足如下函数:
f ( x k ) = 5 k f(x_{k}) = \frac{5}{k} f(xk)=k5
解释:
函数 f ( x k ) = 5 k \begin{aligned} f(x_k) = \frac{5}{k}\end{aligned} f(xk)=k5是我们假设的,隐藏在背后的逻辑。而真正被我们看到的是下面由表格组成的关于 { f ( x k ) } k = 1 ∞ \{f(x_k)\}_{k=1}^{\infty} {f(xk)}k=1∞的序列信息:
其中x 0 x_0 x0是初始化的,不在函数内。这里假设x 0 = 10 x_0 = 10 x0=10,但在本示例中假设的值要> 5 = f ( x 1 ) >5 = f(x_1) >5=f(x1)。之所以要将函数设置成这种格式,是因为基于该函数产生的序列满足事件1:f ( x k + 1 ) < f ( x k ) f(x_{k+1}) < f(x_k) f(xk+1)<f(xk)。
| k k k | 0 ( init ) 0(\text{init}) 0(init) | 1 1 1 | 2 2 2 | 3 3 3 | ⋯ \cdots ⋯ |
|---|---|---|---|---|---|
| f ( x k ) f(x_k) f(xk) | 10 10 10 | 5 5 5 | 5 2 \begin{aligned}\frac{5}{2}\end{aligned} 25 | 5 3 \begin{aligned}\frac{5}{3}\end{aligned} 35 | ⋯ \cdots ⋯ |
至此,我们找到了一组满足事件 1 1 1的由数值解的目标函数结果构成的序列 { f ( x k ) } k = 0 ∞ = { 10 , 5 , 5 2 , 5 3 , ⋯ } \{f(x_k)\}_{k=0}^{\infty} = \left\{10,5,\begin{aligned}\frac{5}{2},\frac{5}{3},\cdots\end{aligned} \right\} {f(xk)}k=0∞={10,5,25,35,⋯},我们观察:这组序列是否能够找到目标函数最优解。
- 初始状态下, [ x 0 , f ( x 0 ) = 10 ] [x_0,f(x_0) = 10] [x0,f(x0)=10]在图中表示如下。
由于此时的梯度仅仅是一个1 1 1维向量,在函数图像中对应函数在该点上的斜率。而在横坐标上,梯度的方向仅有两个:正向(右侧;顺着坐标轴的方向);反向(逆着坐标轴的方向)。因此,图中所说的下降方向必然是最速下降方向(因为只有两个方向)。由于( x 0 , f ( x 0 ) ) (x_0,f(x_0)) (x0,f(x0))在图中对应位置的斜率是正值,因此下一时刻更新的方向必然是负梯度方向(反向),见红色箭头。

- 观察第二个点: [ x 1 , f ( x 1 ) = 5 ] [x_1,f(x_1) = 5] [x1,f(x1)=5],对应图像表示如下:
在该目标函数中,函数值为5 5 5存在两个对应的横坐标。实际上取哪个点都不影响梯度的观察。这里为方便观察,取左侧的横坐标,后续类似情况同理。左侧点斜率是负值,因而它的负梯度方向是正向,见红色箭头。

- 同理,可以将 [ x 2 , f ( x 2 ) = 5 2 ] , [ x 3 , f ( x 3 ) = 5 3 ] \begin{aligned} \left[x_2,f(x_2) = \frac{5}{2}\right],\left[x_3,f(x_3) = \frac{5}{3}\right]\end{aligned} [x2,f(x2)=25],[x3,f(x3)=35]及其对应梯度方向表示在图像上:

- 以此类推。我们可以按照 { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞的顺序,将梯度变化路径用红色箭头描述出来:
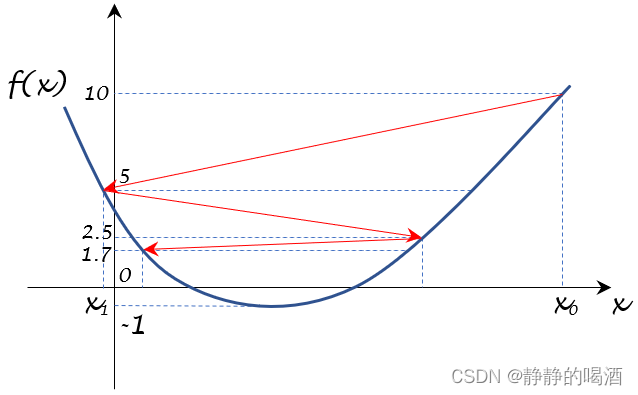
- 从上图可以看出,随着迭代次数 k k k的增加,我们都会产生新的点并震荡下去。但是否能够震荡到最小值呢 ? ? ?这取决于: k → ∞ k \to \infty k→∞时, f ( x k ) f(x_k) f(xk)的取值结果。
lim k → ∞ f ( x k ) = 5 ∞ ≈ 0 \mathop{\lim}\limits_{k \to \infty} f(x_k) = \frac{5}{\infty} \approx 0 k→∞limf(xk)=∞5≈0
最终,它只会在 x x x轴的上方,无限地朝向 0 0 0的方向震荡,而不会越过 x x x轴,向最优值 − 1 -1 −1进行震荡。
综上,上述反例满足事件 1 1 1的条件,但它可能不会一定收敛到最优解。也就是说:仅使用 f ( x k + 1 ) < f ( x k ) f(x_{k+1}) < f(x_k) f(xk+1)<f(xk)对步长 α \alpha α进行判别是不可行的。
上述反例描述的是: { f ( x k ) } k = 0 ∞ \{f(x_k)\}_{k=0}^{\infty} {f(xk)}k=0∞能够收敛,但没有收敛到最优解。
相关参考:
【优化算法】线搜索方法-步长-非确定性搜索
相关文章:

机器学习笔记之优化算法(四)线搜索方法(步长角度;非精确搜索)
机器学习笔记之优化算法——线搜索方法[步长角度,非精确搜索] 引言回顾:精确搜索步长及其弊端非精确搜索近似求解最优步长的条件反例论述 引言 上一节介绍了从精确搜索的步长角度观察了线搜索方法,本节将从非精确搜索的步长角度重新观察线搜…...
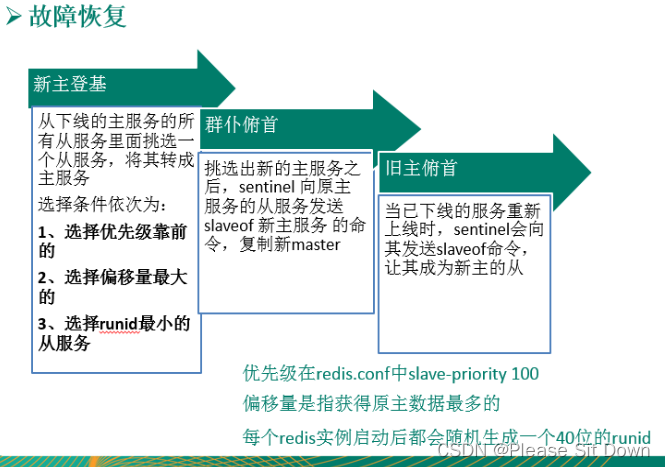
Redis 哨兵 (sentinel)
是什么 官网理论:https://redis.io/docs/management/sentinel/ 吹哨人巡查监控后台 master 主机是否故障,如果故障了根据投票数自动将某一个从库转换为新主库,继续对外服务。 作用:无人值守运维 哨兵的作用: 1…...

统计2021年10月每个退货率不大于0.5的商品各项指标
统计2021年10月每个退货率不大于0.5的商品各项指标_牛客题霸_牛客网s mysql(ifnull): select product_id, format(ifnull(sum(if_click)/nullif(count(*),0),0),3) as ctr, format(ifnull(sum(if_cart)/nullif(sum(if_click),0),0),3) as c…...
【小波尺度谱】从分段离散小波变换计算小波尺度谱研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
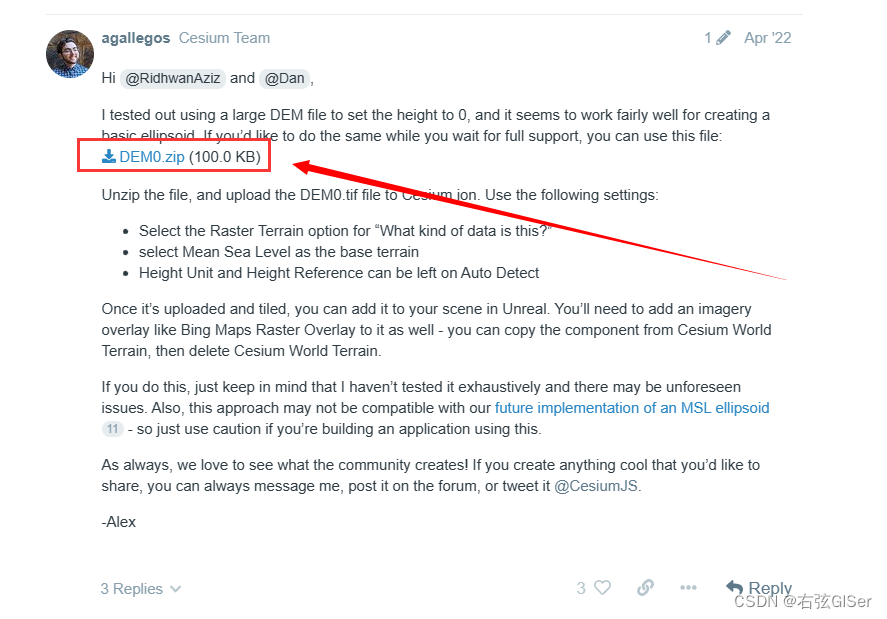
UE5、CesiumForUnreal加载无高度地形
文章目录 1.实现目标2.实现过程3.参考资料1.实现目标 在UE5中,CesiumForUnreal插件默认的地形都是带高度的,这里加载没有高度的地形,即大地高程为0,GIF动图如下: 2.实现过程 参考官方的教程,下载无高度的DEM,再切片加载到UE中。 (1)下载无高度地形DEM0。 在官方帖子…...

关于Spring中的@Configuration中的proxyBeanMethods属性
Configuration的proxyBeanMethods属性 在Configuration注解中,有两个属性: value配置Bean名称proxyBeanMethos,默认是true 这个proxyBeanMethods的默认属性是true。 直接说:当Configuration注解的proxyBeanMeathods属性是true…...

dp1,ACM暑期培训
D - 摆花 P1077 [NOIP2012 普及组] 摆花 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) Description 小明的花店新开张,为了吸引顾客,他想在花店的门口摆上一排花,共 m 盆。通过调查顾客的喜好,小明列出了顾客最喜欢的 n 种花&…...

大厂程序员的水平比非大厂高很多嘛?
最近一个月,筛选了一百多份简历,前前后后面试了二三十人,基本上都是有大厂经历的人。同时,也录用了几个有大厂经历的。但整体而言,打破了对大厂出来的都是优质人才的幻觉。看到的实际情况与想象中的落差还是比较大的。…...
Java开发工具MyEclipse发布v2023.1.2,今年第二个修复版!
MyEclipse一次性提供了巨量的Eclipse插件库,无需学习任何新的开发语言和工具,便可在一体化的IDE下进行Java EE、Web和PhoneGap移动应用的开发;强大的智能代码补齐功能,让企业开发化繁为简。 MyEclipse v2023.1.2官方正式版下载 …...
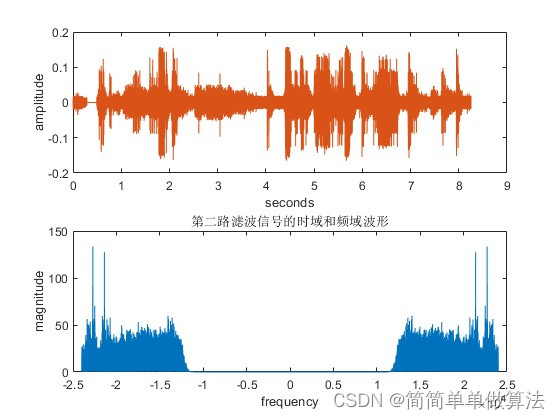
基于正交滤波器组的语音DPCM编解码算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 ...........................................................g0zeros(1,lenH); g1zeros(1,l…...
VS2022和QT混合编程打包发布程序
1.在开始菜单输入 CMD 找到 Qt5.15.2(MSVC 64-bit) 2.输入windeployqt exe所在路径 3.运行完毕后,双击打开exe文件,可能会报错,缺少相关的dll,找到缺少的dll拷贝到运行文件夹下即可。...

Filebeat学习笔记
Filebeat基本概念 简介 Filebeat是一种轻量级日志采集器,内置有多种模块(auditd、Apache、Nginx、System、MySQL等),针对常见格式的日志大大简化收集、解析和可视化过程,只需一条命令即可。之所以能实现这一点&#…...
 —— React17+React Hook+TS4 最佳实践,仿 Jira 企业级项目(十六))
【实战】 九、深入React 状态管理与Redux机制(一) —— React17+React Hook+TS4 最佳实践,仿 Jira 企业级项目(十六)
文章目录 一、项目起航:项目初始化与配置二、React 与 Hook 应用:实现项目列表三、TS 应用:JS神助攻 - 强类型四、JWT、用户认证与异步请求五、CSS 其实很简单 - 用 CSS-in-JS 添加样式六、用户体验优化 - 加载中和错误状态处理七、Hook&…...

第九十五回 如何使用dio的转换器
文章目录 概念介绍使用方法使用默认的转换器自定义转换器 示例代码经验分享 我们在上一章回中介绍了"如何打造一个网络框架"相关的内容,本章回中将介绍 如何使用dio的转换器.闲话休提,让我们一起Talk Flutter吧。 概念介绍 转换器主要用来转…...

Python深度学习“四大名著”之一【赠书活动|第二期《Python机器学习:基于PyTorch和Scikit-Learn》】
近年来,机器学习方法凭借其理解海量数据和自主决策的能力,已在医疗保健、 机器人、生物学、物理学、大众消费和互联网服务等行业得到了广泛的应用。自从AlexNet模型在2012年ImageNet大赛被提出以来,机器学习和深度学习迅猛发展,取…...
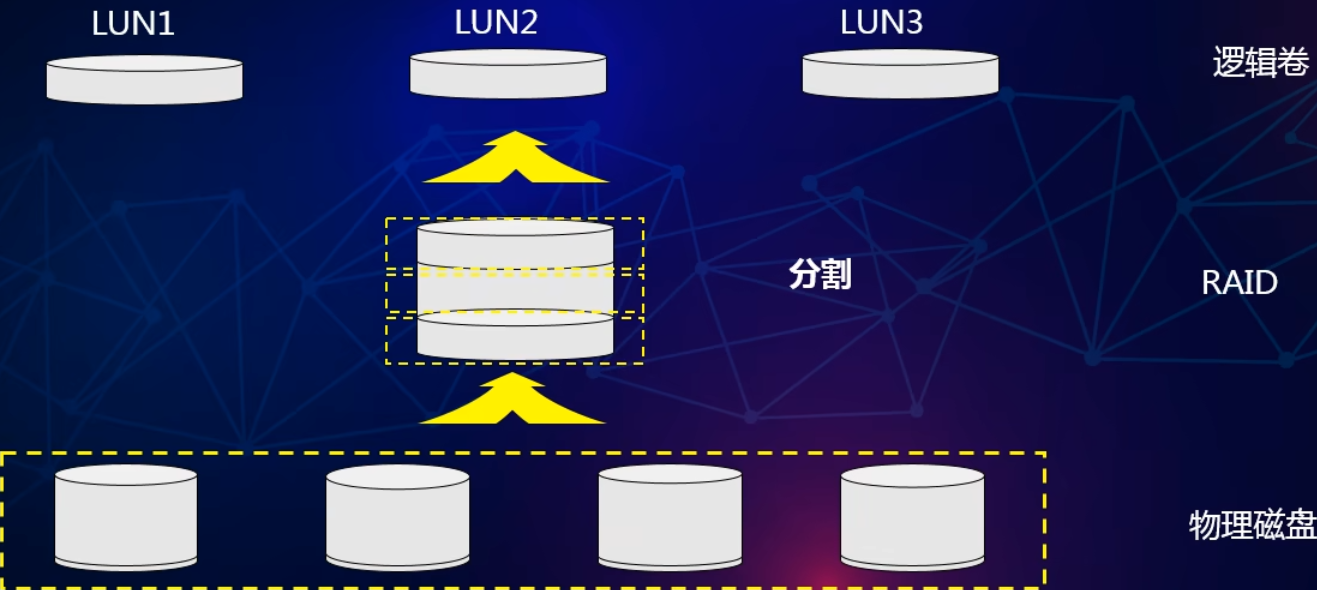
RAID相关知识
简介 RAID ( Redundant Array of Independent Disks )即独立磁盘冗余阵列,通常简称为磁盘阵列。RAID技术将多个单独的物理硬盘以不同的方式组合成一个逻辑磁盘,从而提高硬盘的读写性能和数据安全性。 数据组织形式 分块&#x…...
DataStructure--Basic
程序设计数据结构算法 只谈数据结构不谈算法就跟去话剧院看梁山伯与祝英台结果只有梁山伯在演,祝英台生病了没来一样。 本文的所有内容都出自《大话数据结构》这本书中的代码实现部分,建议看书,书中比我本文写的全。 数据结构,直…...
Intellij IDEA 双击启动报错ClassNotFoundException: com.licel.b.z@
项目场景: 新从官网下载了ideaIU-2023.2.win.zip ,安装后双击启动报错, 无法运行idea, 提示信息如下 问题描述 Internal error. Please refer to https://jb.gg/ide/critical-startup-errorsjava.lang.ExceptionInInitializerErrorat java…...
使用 Logstash 及 enrich processor 实现数据丰富自动化
在我之前的文章: Elasticsearch:enrich processor (7.5发行版新功能) Elasticsearch:使用 Elasticsearch ingest pipeline 丰富数据 通过上面的两篇文章的介绍,我们应该充分掌握了如何使用 enrich proce…...
Django模板语法和请求
1、在django关于模板文件加载顺序 创建的django项目下会有一个seeetings.py的文件 如果在seeetings.py 中加了 os.path.join(BASE_DIR,‘templates’),如果是pycharm创建的django项目会加上,就会默认先去根目录找templates目录下的html文件,…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
