【图论】树上差分(边差分)
一.简介
其实点差分和边差分区别不大。
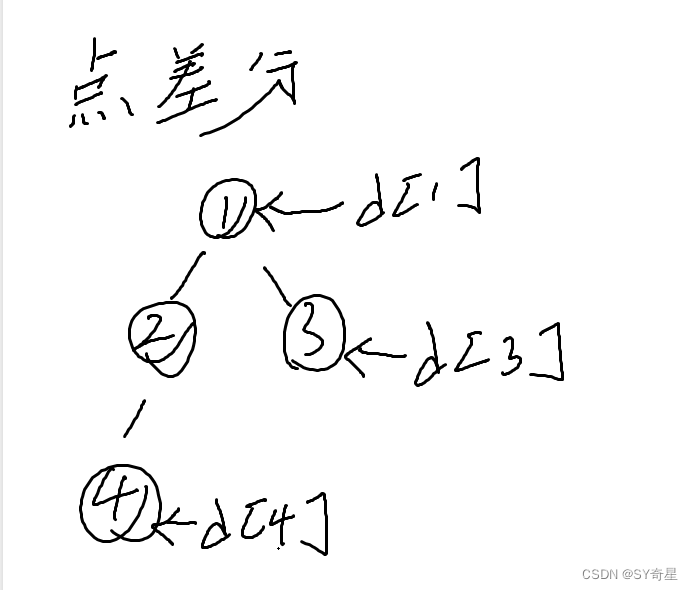
点差分中,d数组存储的是树上的节点
边差分中,d数组存储的是当前节点到父节点的那条边的差分值。
指定注意的是:边差分中因为根连的父节点是虚点,所以遍历结果时应当忽略!

二.题目

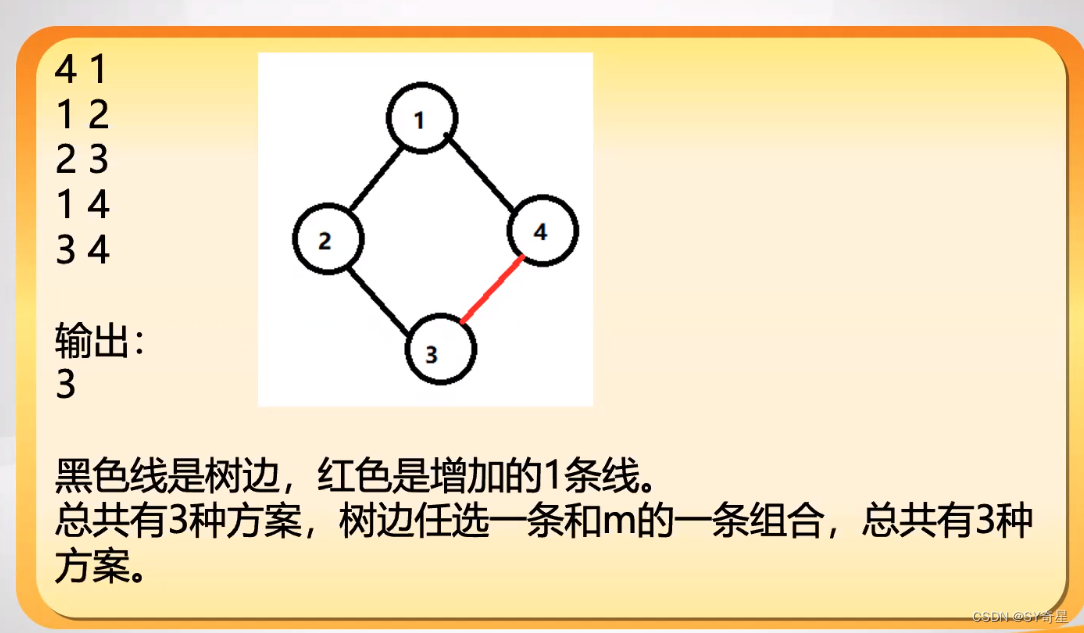
样例输入:
4 1
1 2
2 3
1 4
3 4样例输出:3
三.题目分析
我们易知:
加上一条边时,相当于把所经过的节点都加了一条命。(这时用差分快一些)
(为了方便,我们令边的权值为-1时,才算断掉)
若一条边最后还是没加命,即0;所以切断它,图就不连通了,所以红边任意切一条即可。所以此边贡献为m;
若这条边有一条命,我们切断它后,它还有一条命,固只能再切掉给它续命的那条红边,图才不联通,所以此边贡献为1;
若这条边有2条以及以上条命,我们显然要切3次及三次以上。但我们只能切二次。它命太硬了,所以我们放弃这条边。次边贡献为0;
四.参考代码
/*
4 1
1 2
2 3
1 4
3 4
*/#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
int n,m;
struct Edge{int u,v,next;
}edge[maxn<<1];
int head[maxn],cnt=0;
void add(int u,int v){edge[++cnt]=(Edge){u,v,head[u]}; head[u]=cnt;
}
int depth[maxn],p[maxn][30],d[maxn];
void dfs1(int u,int fa){depth[u]=depth[fa]+1;p[u][0]=fa;for(int i=1;(1<<i)<=depth[u];i++){p[u][i]=p[p[u][i-1]][i-1];}for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(fa!=v) dfs1(v,u);}
}
int LCA(int x,int y){if(depth[x]<depth[y]) swap(x,y);int lg=0;while((1<<lg)<=depth[x]) lg++;for(int i=lg;i>=0;i--){if(depth[x]-(1<<i)>=depth[y]){x=p[x][i];}}if(x==y) return x;for(int i=lg;i>=0;i--){if(p[x][i]!=p[y][i]){x=p[x][i]; y=p[y][i];}}return p[x][0];
}
void dfs2(int u,int fa){for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(v!=fa){dfs2(v,u);d[u]+=d[v];}}
}
int main(){//读入数据 scanf("%d%d",&n,&m);int u,v;for(int i=1;i<n;i++){scanf("%d%d",&u,&v);add(u,v); add(v,u);}//建树 dfs1(1,0);for(int i=1;i<=m;i++){scanf("%d%d",&u,&v);d[u]++; d[v]++;int lca=LCA(u,v);d[lca]-=2;}//sum原数组dfs2(1,0); int ans=0;//i从2开始,因为1连的父节点是虚点 for(int i=2;i<=n;i++){if(d[i]==0) ans+=m;else if(d[i]==1) ans++;}cout<<ans;return 0;
}相关文章:

【图论】树上差分(边差分)
一.简介 其实点差分和边差分区别不大。 点差分中,d数组存储的是树上的节点 边差分中,d数组存储的是当前节点到父节点的那条边的差分值。 指定注意的是:边差分中因为根连的父节点是虚点,所以遍历结果时应当忽略! 二…...
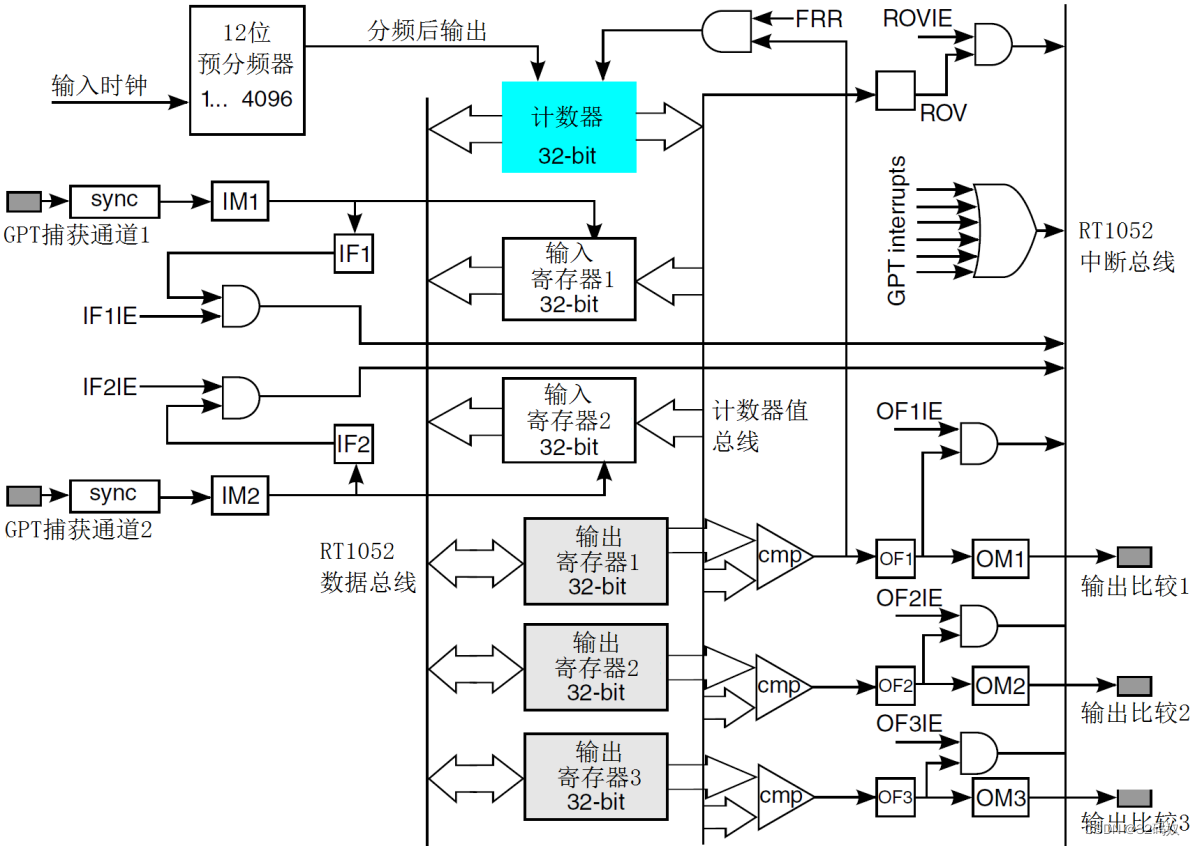
RT1052的定时器
文章目录 1 通用定时器1.1 定时器框图1.2 实现周期性中断 2 相关寄存器3 定时器配置3.1 时钟使能3.2 初始化GPT1定时器3.2.1 base3.2.2 initConfig3.2.2.1 clockSorce3.2.2.2 divider3.2.2.3 enablexxxxx 3.3 设置 GPT1 比较值3.3.1 base3.3.2 channel3.3.3 value 3.4 设置 GPT…...
opencv python 训练自己的分类器
源码下载 一、分类器制作 1.样本准备 收集好你所需的正样本,和负样本,分别保存在不同文件夹 在pycharm新建项目,项目结构如下:has_mask文件夹放置正样本,no_mask文件夹放置负样本 安装opencv,把opencv包…...
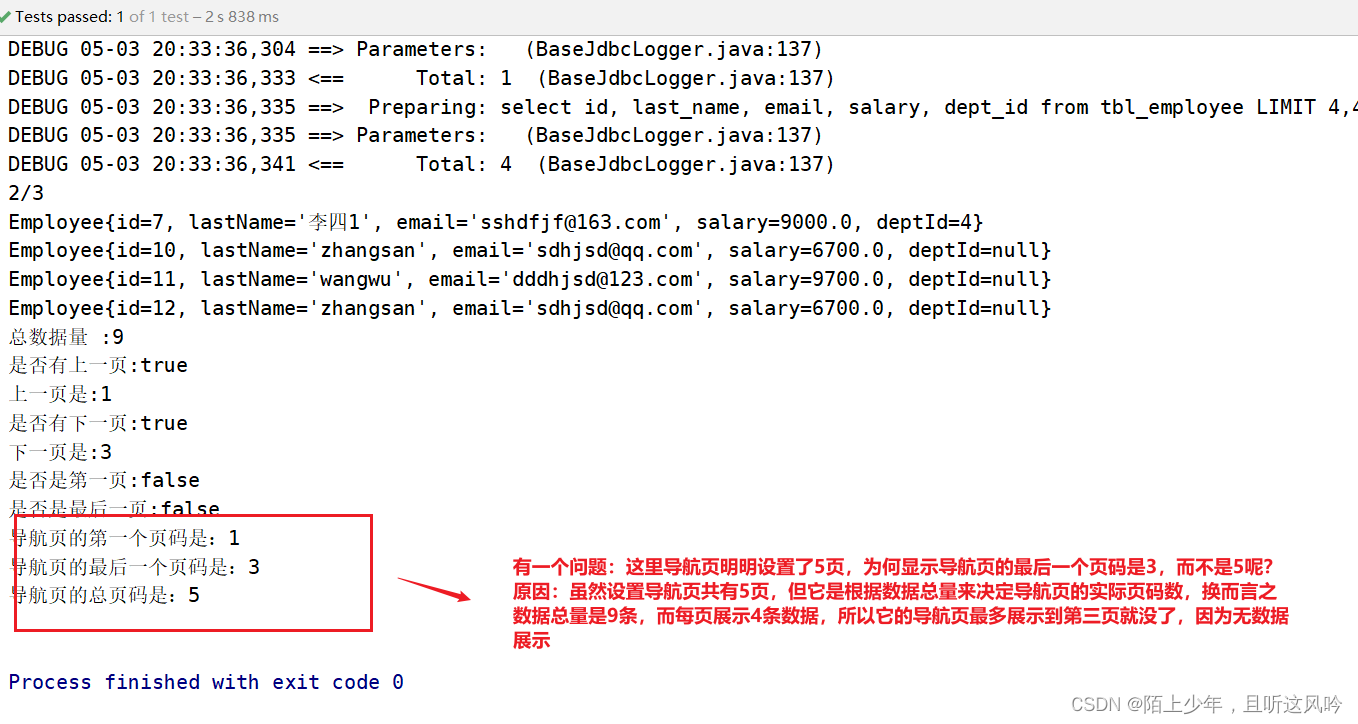
详解Mybatis之分页插件【PageHelper】
编译软件:IntelliJ IDEA 2019.2.4 x64 操作系统:win10 x64 位 家庭版 Maven版本:apache-maven-3.6.3 Mybatis版本:3.5.6 文章目录 一. 什么是分页?二. 为什么使用分页?三. 如何设计一个Page类(分…...
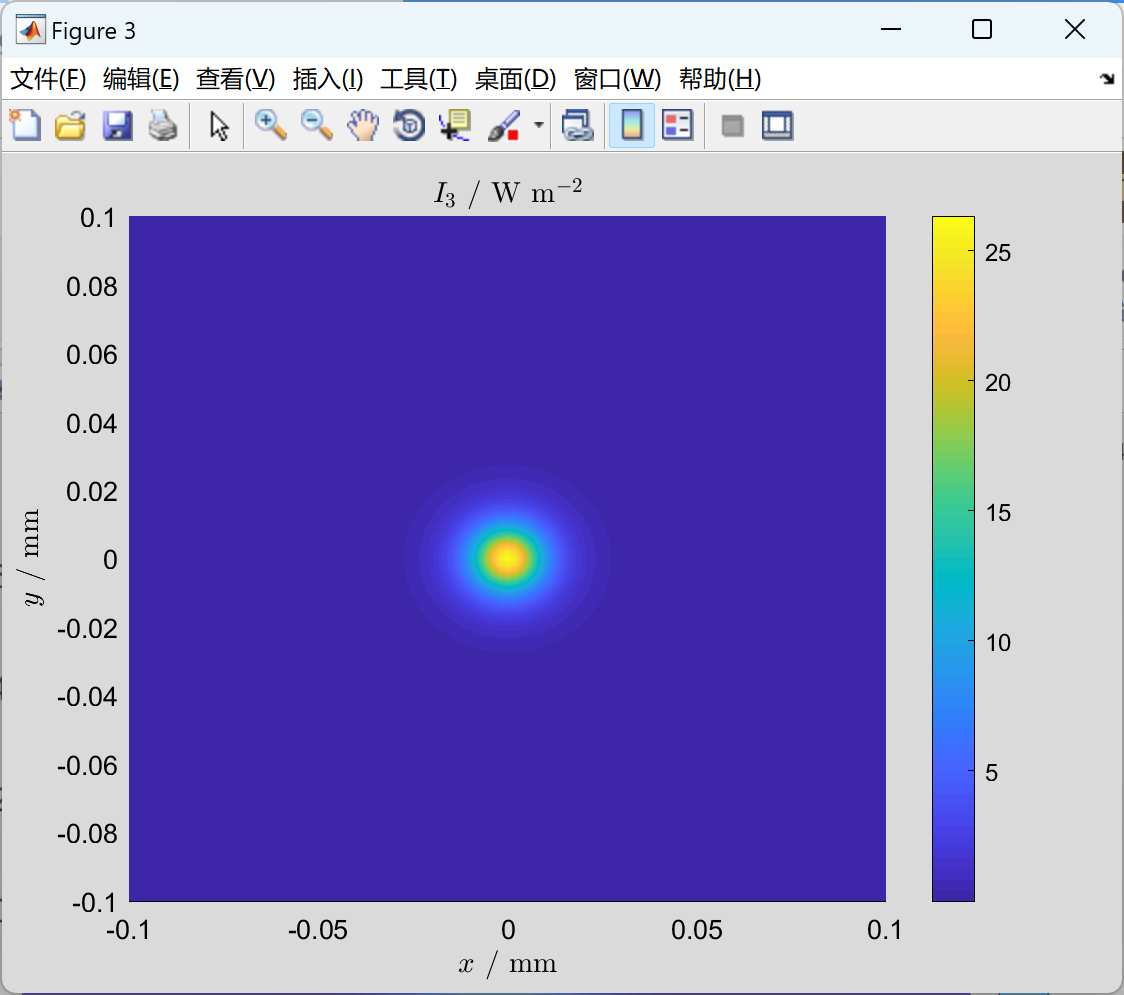
【基于矢量射线的衍射积分 (VRBDI)】基于矢量射线的衍射积分 (VRBDI) 和仿真工具(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

基于jackson对bean的序列号和反序列化
通过观察控制台输出的SQL发现页面传递过来的员工id的值和数据库中的id值不一致,这是怎么回事呢? 分页查询时服务端响应给页面的数据中id的值为19位数字,类型为long 页面中js处理long型数字只能精确到前16位,所以最终通过ajax请求提交给服务…...

排队理论简介
排队理论简介 1. 理论背景2. 研究的数学方法3. 拒绝型排队系统与等候型排队系统4. 拒绝型排队系统 本文参考文献为Вентцель Е. С.的《Исследование операций》。 1. 理论背景 排队理论又称大众服务理论,顾名思义指的是在有限的服务条…...
-算法分析)
极速查找(3)-算法分析
篇前小言 本篇文章是对查找(2)的续讲二叉排序树 二叉排序树(Binary Search Tree,BST),又称为二叉查找树,是一种特殊的二叉树。性质: 左子树的节点值小于根节点的值,右…...

http 常见的响应状态码 ?
100——客户必须继续发出请求101——客户要求服务器根据请求转换HTTP协议版本200——交易成功201——提示知道新文件的URL202——接受和处理、但处理未完成203——返回信息不确定或不完整204——请求收到,但返回信息为空205——服务器完成了请求,用户代理…...
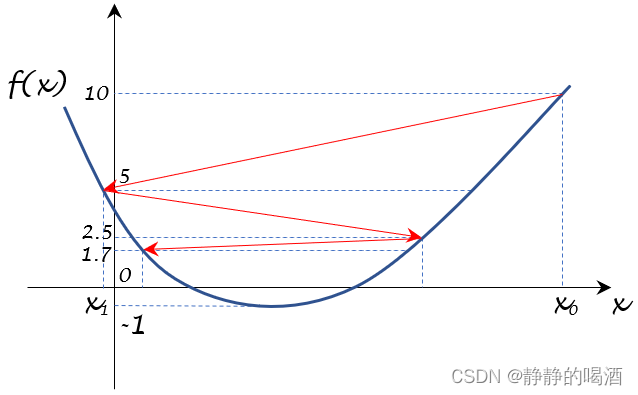
机器学习笔记之优化算法(四)线搜索方法(步长角度;非精确搜索)
机器学习笔记之优化算法——线搜索方法[步长角度,非精确搜索] 引言回顾:精确搜索步长及其弊端非精确搜索近似求解最优步长的条件反例论述 引言 上一节介绍了从精确搜索的步长角度观察了线搜索方法,本节将从非精确搜索的步长角度重新观察线搜…...
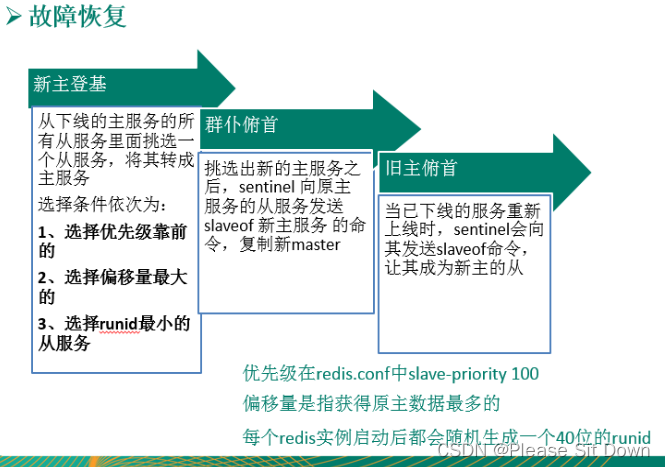
Redis 哨兵 (sentinel)
是什么 官网理论:https://redis.io/docs/management/sentinel/ 吹哨人巡查监控后台 master 主机是否故障,如果故障了根据投票数自动将某一个从库转换为新主库,继续对外服务。 作用:无人值守运维 哨兵的作用: 1…...

统计2021年10月每个退货率不大于0.5的商品各项指标
统计2021年10月每个退货率不大于0.5的商品各项指标_牛客题霸_牛客网s mysql(ifnull): select product_id, format(ifnull(sum(if_click)/nullif(count(*),0),0),3) as ctr, format(ifnull(sum(if_cart)/nullif(sum(if_click),0),0),3) as c…...
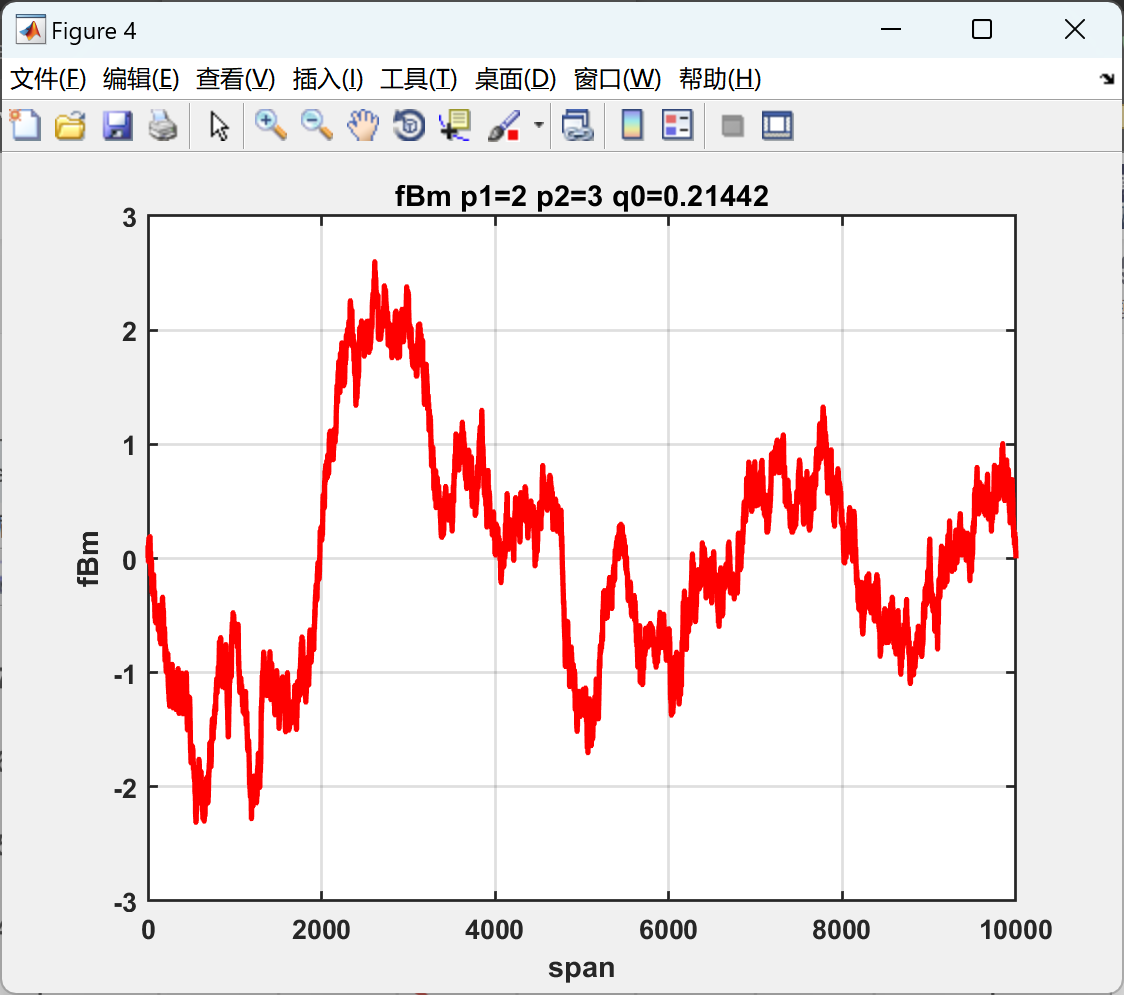
【小波尺度谱】从分段离散小波变换计算小波尺度谱研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
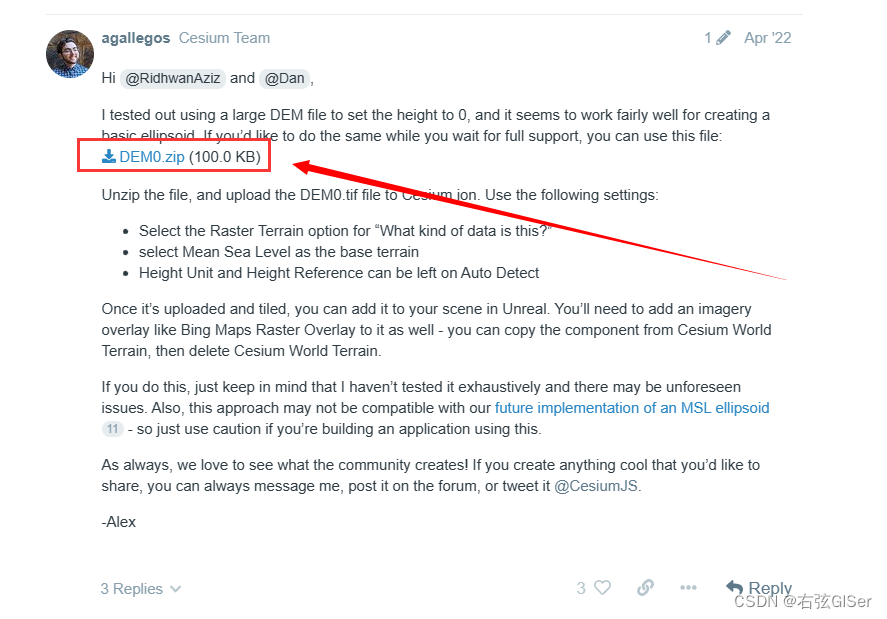
UE5、CesiumForUnreal加载无高度地形
文章目录 1.实现目标2.实现过程3.参考资料1.实现目标 在UE5中,CesiumForUnreal插件默认的地形都是带高度的,这里加载没有高度的地形,即大地高程为0,GIF动图如下: 2.实现过程 参考官方的教程,下载无高度的DEM,再切片加载到UE中。 (1)下载无高度地形DEM0。 在官方帖子…...

关于Spring中的@Configuration中的proxyBeanMethods属性
Configuration的proxyBeanMethods属性 在Configuration注解中,有两个属性: value配置Bean名称proxyBeanMethos,默认是true 这个proxyBeanMethods的默认属性是true。 直接说:当Configuration注解的proxyBeanMeathods属性是true…...

dp1,ACM暑期培训
D - 摆花 P1077 [NOIP2012 普及组] 摆花 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) Description 小明的花店新开张,为了吸引顾客,他想在花店的门口摆上一排花,共 m 盆。通过调查顾客的喜好,小明列出了顾客最喜欢的 n 种花&…...

大厂程序员的水平比非大厂高很多嘛?
最近一个月,筛选了一百多份简历,前前后后面试了二三十人,基本上都是有大厂经历的人。同时,也录用了几个有大厂经历的。但整体而言,打破了对大厂出来的都是优质人才的幻觉。看到的实际情况与想象中的落差还是比较大的。…...
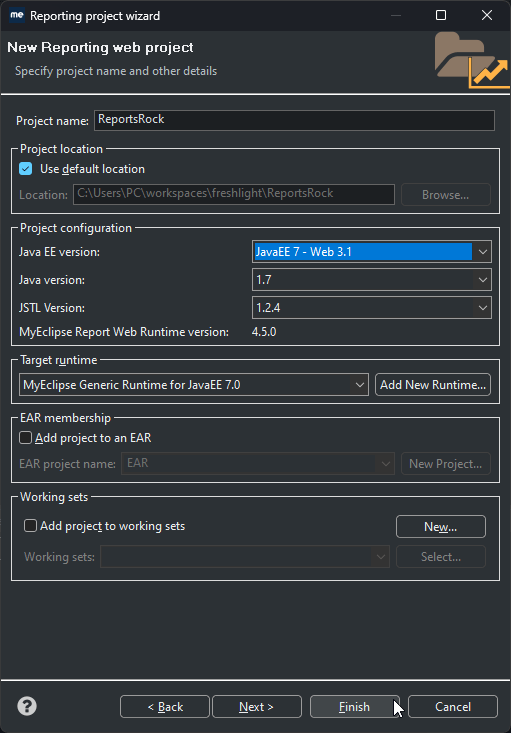
Java开发工具MyEclipse发布v2023.1.2,今年第二个修复版!
MyEclipse一次性提供了巨量的Eclipse插件库,无需学习任何新的开发语言和工具,便可在一体化的IDE下进行Java EE、Web和PhoneGap移动应用的开发;强大的智能代码补齐功能,让企业开发化繁为简。 MyEclipse v2023.1.2官方正式版下载 …...
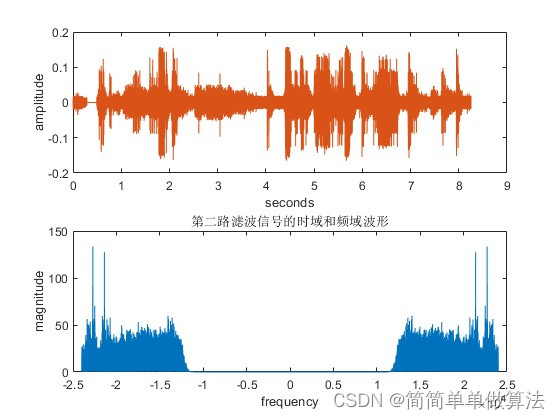
基于正交滤波器组的语音DPCM编解码算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 ...........................................................g0zeros(1,lenH); g1zeros(1,l…...
VS2022和QT混合编程打包发布程序
1.在开始菜单输入 CMD 找到 Qt5.15.2(MSVC 64-bit) 2.输入windeployqt exe所在路径 3.运行完毕后,双击打开exe文件,可能会报错,缺少相关的dll,找到缺少的dll拷贝到运行文件夹下即可。...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
