【C++】优先级队列的基本概念以及其模拟实现
文章目录
- 补充知识:仿函数
- 一、优先级队列:
- 1.引入
- 2.介绍
- 二、priority_queue的模拟实现
- 1.大体框架
- 2.私有成员函数:
- 1.向下调整(AdjustDown)
- 2.向上调整(AdjustUp)
- 3.公有成员函数
- 1大小(size).
- 2是否为空(empty).
- 3.移除堆顶的元素(pop)
- 4.元素插入(push)
- 5.堆顶的元素(top)
- 6.构造函数
- 1.默认无参构造
- 2.迭代器构造
补充知识:仿函数
C++仿函数(function object)是一种可以像函数一样调用的对象。仿函数通常是一个类,它重载了函数调用运算符operator(),使得对象可以被调用。

一、优先级队列:
1.引入
优先级队列(Priority Queue)在底层实现上使用了一种称为堆(Heap)的数据结构,通常使用数组(比如C++中的std::vector)来表示。堆是一种完全二叉树数据结构,具有以下特点:
- 堆是一个完全二叉树,也就是说除了最底层,其他层都必须是完全填满的,最底层的节点依次从左到右填充。
2.堆中的每个节点的值都大于等于(或小于等于)其子节点的值,这就是所谓的堆序性质。
2.介绍
- 优先队列是一种容器适配器,根据严格的弱排序标准,它的第一个元素总是它所包含的元素中最大的。
- 此上下文类似于堆,在堆中可以随时插入元素,并且只能检索最大堆元素(优先队列中位于顶部的元素)。
- 优先队列被实现为容器适配器,容器适配器即将特定容器类封装作为其底层容器类
- 底层容器可以是任何标准容器类模板,也可以是其他特定设计的容器类。容器应该可以通过随机访问迭
代器访问,并支持以下操作:
empty():检测容器是否为空
size():返回容器中有效元素个数
front():返回容器中第一个元素的引用
push_back():在容器尾部插入元素
pop_back():删除容器尾部元素- 标准容器类vector和deque满足这些需求。默认情况下,如果没有为特定的priority_queue类实例化指定容器类,则使用vector。
虽然底层实现中使用了vector,但优先级队列仍然保持了队列的特性,即根据优先级出队元素
二、priority_queue的模拟实现
1.大体框架
namespace simulation {
template<class T, class Container = vector<T>, class Compare = less<T>>//Compare这里传的是仿函数,默认为系统里自带的less仿函数,也可以自己添加//用于比较大小,Container为底层实现容器,默认为vectorclass priority_queue {private://私有成员函数void AdjustDown(int parent) { }void AdjustUp(int child) {}public://公有成员函数void pop() { }void push(const T & x) {}const T& top() { }bool empty() {}size_t size() {}priority_queue(){}private:Container _con;//成员变量};
2.私有成员函数:
1.向下调整(AdjustDown)
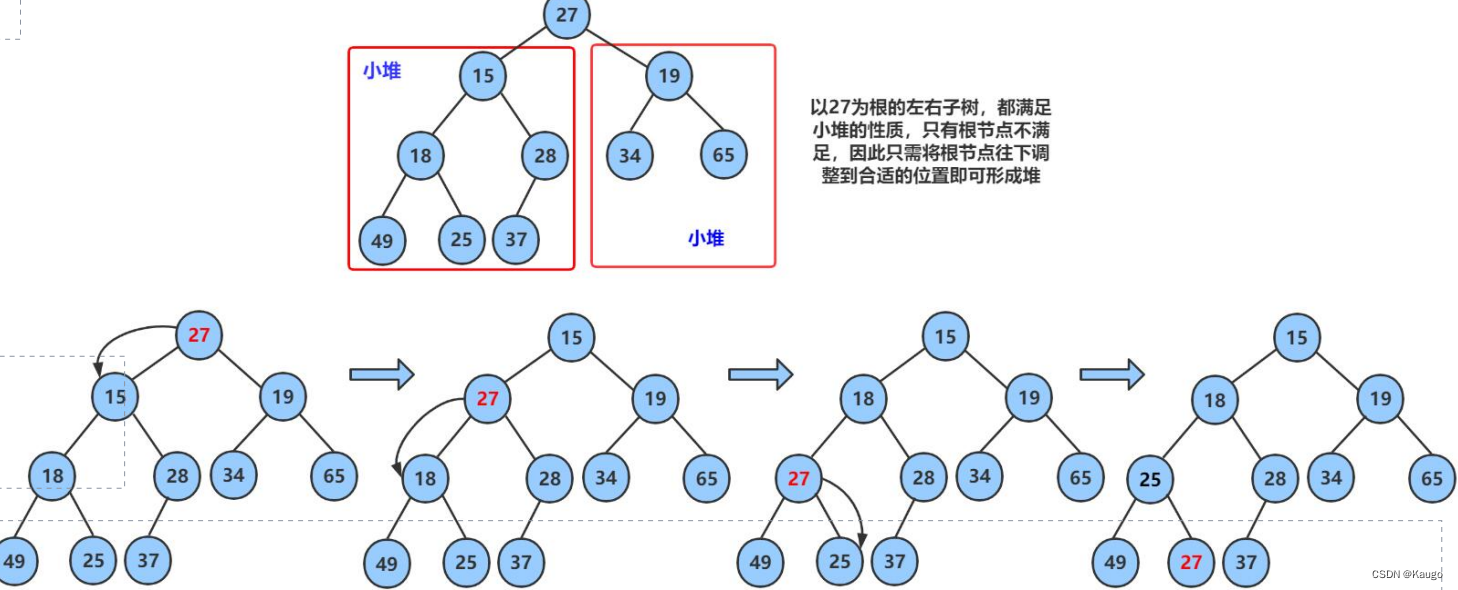
图中是在建小堆,但我们代码以大堆为例,除了大于小于的方向不同,但逻辑是一样的
void AdjustDown(int parent) {//向下调整条件:// 左右子树都是大堆/小堆int child = parent * 2 + 1;Compare com;//仿函数的实例化while (child < _con.size()) {if (child + 1 < _con.size() && com(_con[child], _con[child + 1])) {++child;//选出两个孩子中最大的那一个}if (com(_con[parent], _con[child])) {//最大的那一个去与父母比较swap(_con[parent], _con[child]);parent = child;child = parent * 2 + 1;}else {break;}}}
2.向上调整(AdjustUp)
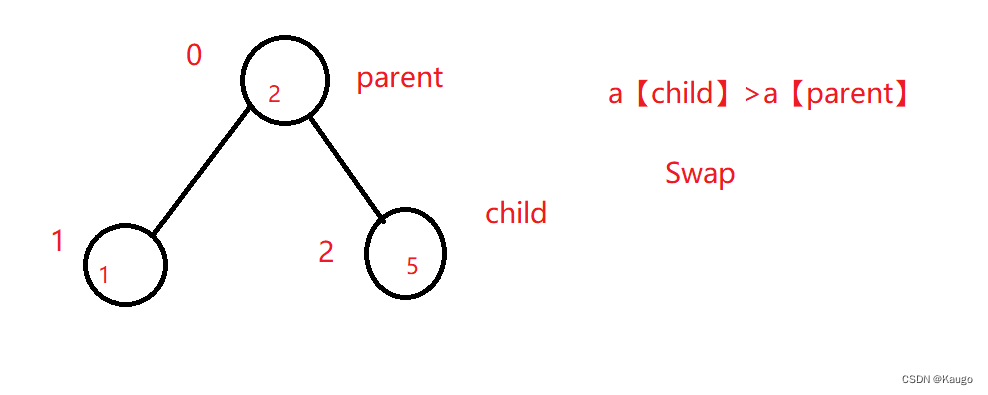
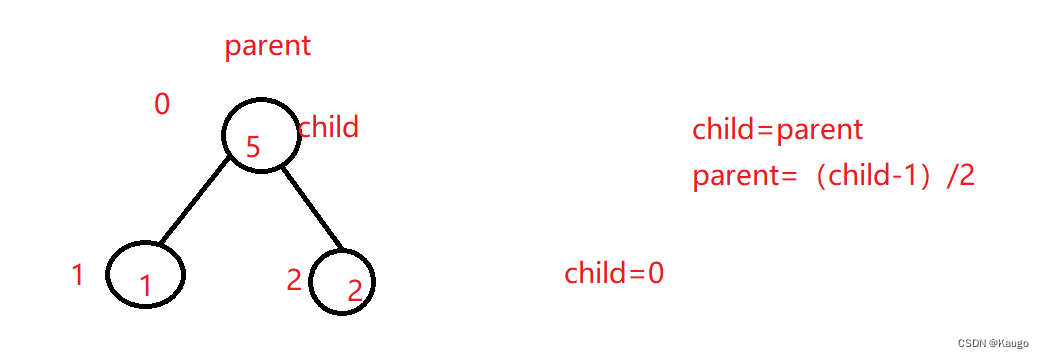
void AdjustUp(int child) {//向上调整条件:// 除了child这个位置前面的数据构成堆int parent = (child - 1) / 2;Compare com;while (child > 0) {if (com(_con[parent], _con[child])) {swap(_con[parent], _con[child]);child = parent;//接着向上parent = (child - 1) / 2;}else {break;}}}
3.公有成员函数
1大小(size).
2是否为空(empty).
3.移除堆顶的元素(pop)

void pop() {swap(_con[0], _con[_con.size() - 1]);_con.pop_back();AdjustDown(0);}
4.元素插入(push)
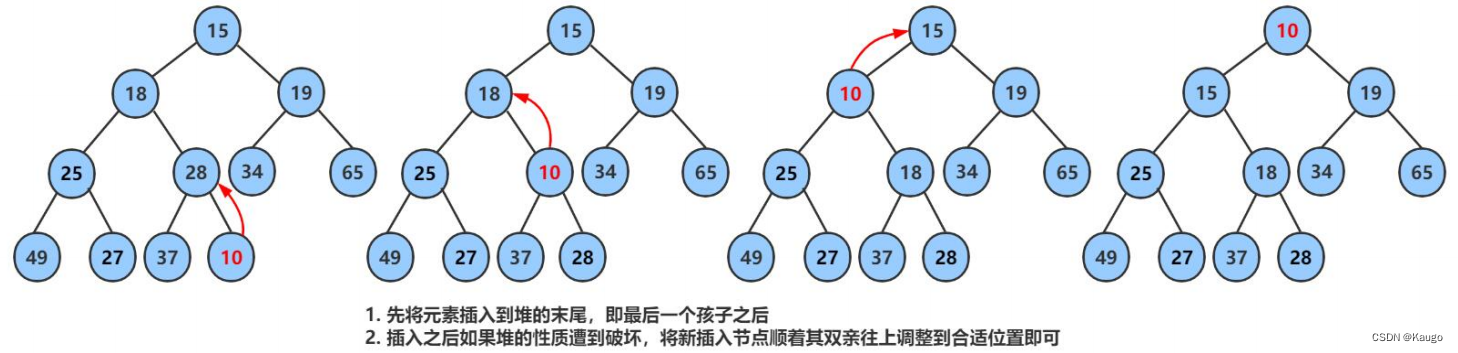
void push(const T& x) {_con.push_back(x);//新元素向上调整AdjustUp(_con.size() - 1);}
5.堆顶的元素(top)
const T& top() {return _con[0];}
6.构造函数
1.默认无参构造
priority_queue() {
//内容可以什么都不写,因为初始化会去内置类型不用管,自定义类型会去调用其
//默认构造函数,这里会直接调用成员变量_con的默认构造
//当你写了迭代器构造后,这个无参构造你必须要有,因为当你写了一个构造函数
//以后,编译器就不会自己再生成默认构造函数}
2.迭代器构造
template<class InputIterator>priority_queue(InputIterator first, InputIterator last) {while (first != last) {_con.push_back(*first);++first;}for (int i = (_con.size() - 1 - 1) / 2; i >= 0; i--) {AdjustDown(i);}}
相关文章:

【C++】优先级队列的基本概念以及其模拟实现
文章目录 补充知识:仿函数一、优先级队列:1.引入2.介绍 二、priority_queue的模拟实现1.大体框架2.私有成员函数:1.向下调整(AdjustDown)2.向上调整(AdjustUp) 3.公有成员函数1大小(…...
TextClamp for Vue3.0(Vue3.0的文本展开收起组件)
呦!大家好,好久没有更新博客了,最近实现了一个一直想自己完成的一个东西,就是文本的展开收起组件,以前项目需要用到,自己实现一个又太繁琐,所以那个时候都是用的别人的轮子,现在自己…...

区间预测 | MATLAB实现VAR向量自回归时间序列区间预测
区间预测 | MATLAB实现VAR向量自回归时间序列区间预测 目录 区间预测 | MATLAB实现VAR向量自回归时间序列区间预测预测效果基本介绍程序设计参考资料预测效果 基本介绍 区间预测 | MATLAB实现VAR向量自回归时间序列区间预测 VAR(Vector Autoregression)模型是一种广泛应用于时…...

在 Windows 上搭建 NTP 服务器
文章目录 一、基础环境二、适用场景三、操作步骤四、常用的NTP服务器五、参考资料 版权声明:本文为博主原创文章,于2023年7月30日首发于CSDN,转载请附上原文出处链接和本声明。本文链接:https://blog.csdn.net/u011046671 一、基础…...
应急响应经典案例-FTP 暴力破解
应急响应经典案例-FTP 暴力破解 应急场景日志分析应急处理措施 应急场景 从昨天开始,网站响应速度变得缓慢,网站服务器登录上去非常卡,重启服务器就能保证一段时间的正常访问,网站响应状态时而飞快时而缓慢,多数时间是…...

41. linux通过yum安装postgresql
文章目录 1.下载安装包2.关闭内置PostgreSQL模块:3.安装postgresql服务:4.初始化postgresql数据库:5.设置开机自启动:6.启动postgresql数据库7.查看postgresql进程8.通过netstat命令或者lsof 监听默认端口54329.使用find命令查找了一下postgresql.conf的配置位置10.修改postgre…...

SpringBoot启动流程及自动配置
SpringBoot启动流程源码: 1、启动SpringBoot启动类SpringbootdemoApplication中的main方法。 SpringBootApplication public class SpringbootdemoApplication {public static void main(String[] args) {SpringApplication.run(SpringbootdemoApplication.class, …...

【Linux】进程轻松入门
目录 一, 冯* 诺依曼体系结构 1,存储结构 编辑 二, 操作系统 1,概念 2,设计OS的目的 3,定位 4,如何理解 "管理" 5, 总结 三,进程 1. 概念 那么…...
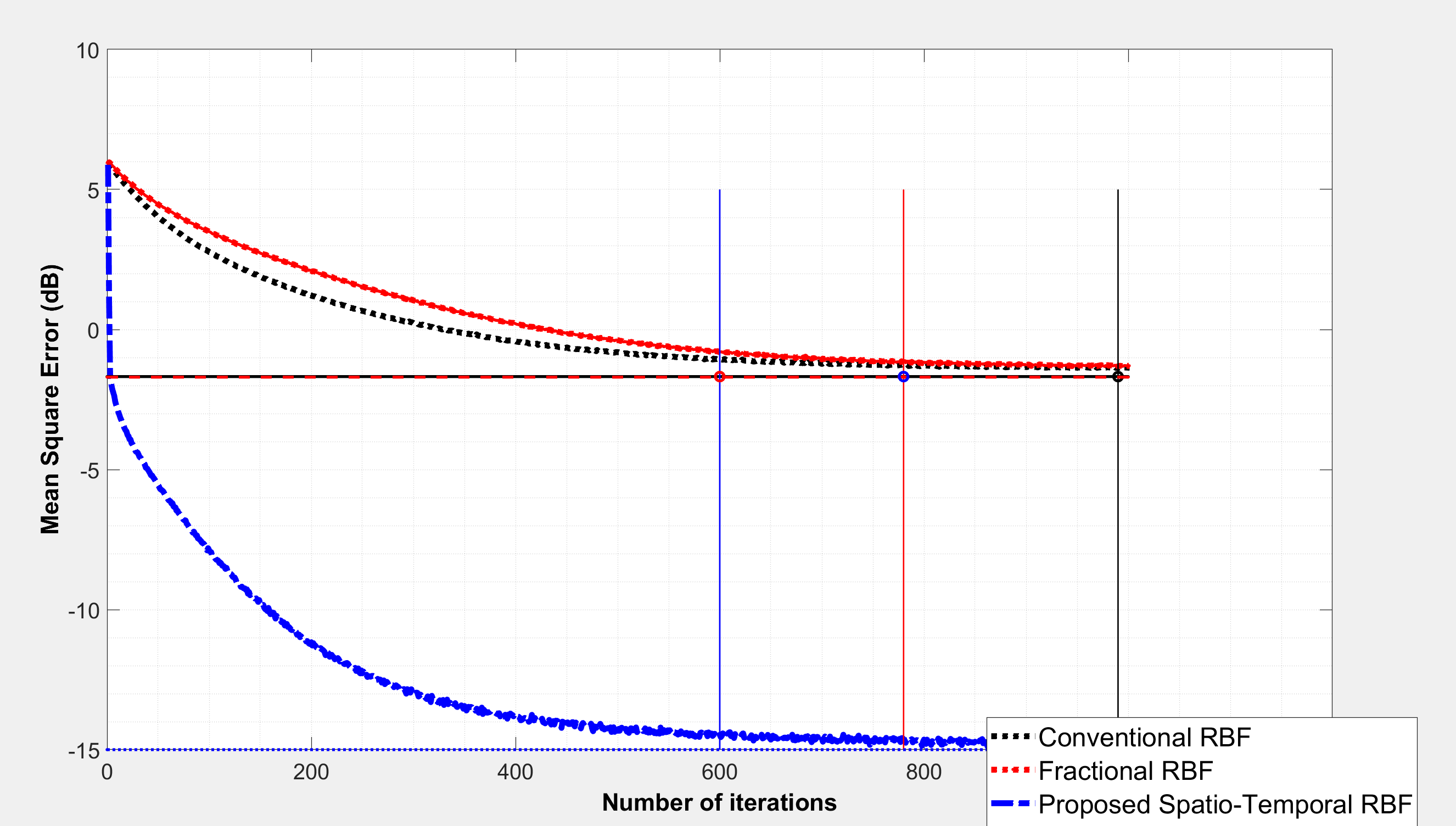
【使用时空RBF-NN进行非线性系统识别】实现了 RBF、分数 RBF 和时空 RBF 神经网络,用于非线性系统识别研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Tomcat 安装配置教程及成功后,启动失败报错解决方案
解决方案 我的报错原因是因为我的JDK是1.8的而我的Tomcat是10版本的,可能是因为版本原因吧,我重新装了Tomcat 9就可以启动成功了! 简单说下安装的时候需要注意哪些步骤吧 今天我在安装tomcat10的时候,安装成功后,启…...
C#文件操作从入门到精通(2)——查看某个dll中有哪些函数
kernel32.dll中含有ini文件操作使用的函数,我们可以通过VisualStudio自带的dumpbin.exe查看dll所包含的函数,操作步骤如下: 1、找到dumpbin.exe所在的文件夹 我的电脑中安装了VisualStudio2019社区版以及VisualStudio2017Professional,但是我发现VisualStudio2019社区版中…...
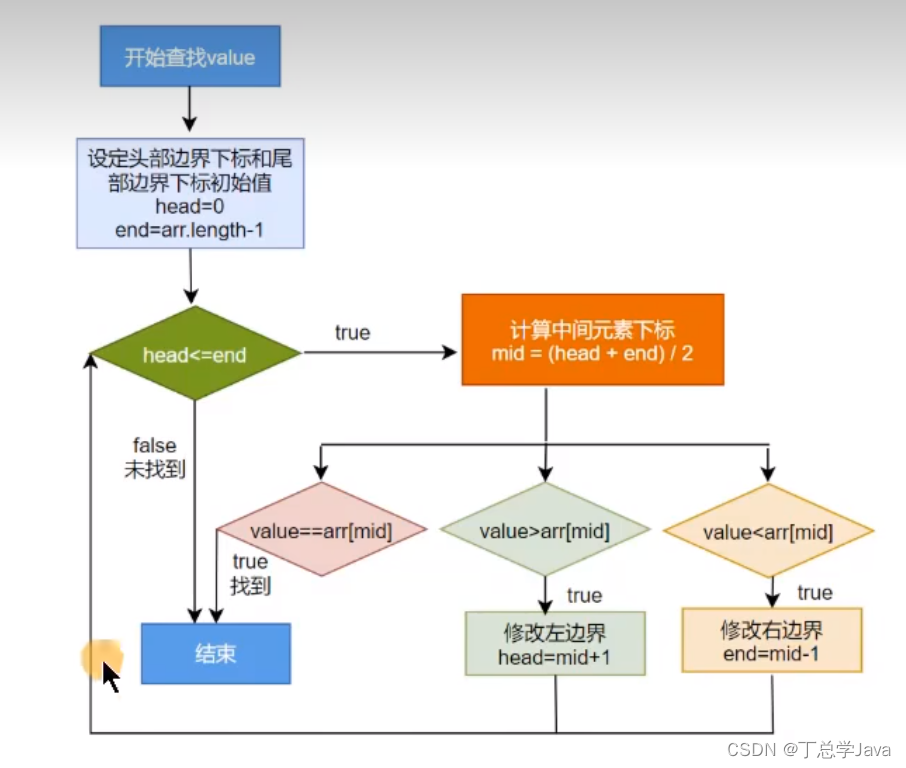
二分查找算法(全网最详细代码演示)
二分查找也称 半查找(Binary Search),它时一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字 有序 排列。 注意:使用二分查找的前提是 该数组是有序的。 在实际开…...

draw up a plan
爱情是美好的,却不是唯一的。爱情只是属于个人化的感情。 推荐一篇关于爱情的美文: 在一个小镇上,有一家以制作精美巧克力而闻名的手工巧克力店,名叫“甜蜜之爱”。这家巧克力店是由一位名叫艾玛的年轻女性经营的,她对…...

抖音seo源码开发源代码开发技术分享
一、 抖音SEO源码开发,需要掌握以下技术: 抖音API接口:抖音提供了丰富的API接口,包括用户信息、视频信息、评论信息等。 数据爬取技术:通过抓包分析抖音接口的数据结构,可以使用Python等编程语言编写爬虫程…...
)
QEMU(Quick Emulator)
QEMU(Quick Emulator)是一款由法布里斯贝拉等人编写的免费的可执行硬件虚拟化的开源托管虚拟机。它可以通过动态的二进制转换模拟CPU,并提供一组设备模型,使它能够运行多种未修改的客户机OS。QEMU还可以为user-level的进程执行CPU…...
无效问题)
Gateway结合nacos(lb://xxx)无效问题
Gateway结合nacos无效 版本如下: com.alibaba.cloud:spring-cloud-starter-alibaba-nacos-discovery:2021.0.1.0 org.springframework.cloud:spring-cloud-starter-gateway:3.1.1 配置如下: server:port: 7000 spring:application:name: springCloudGa…...
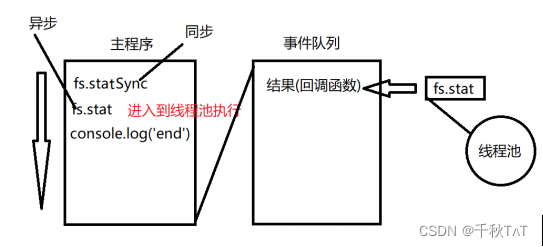
NODEJS笔记
全局对象 global/window console.log/info/warn/error/time/timeEnd process.arch/platform/version/env/kill/pid/nextTick Buffer.alloc(5,abcde) String/toString setTimeout/clearTimeout setInterval/clearInterval setImmediate/clearImmediate process.nextTi…...
方法函数)
无涯教程-jQuery - html( )方法函数
html(val)方法获取第一个匹配元素的html内容(innerHTML)。此属性在XML文档上不可用。 html( ) - 语法 selector.html( ) html( ) - 示例 以下是一个简单的示例,简单说明了此方法的用法- <html><head><title>The jQuery Example</title>…...
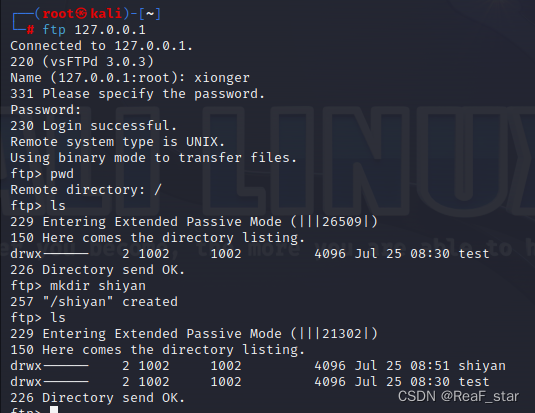
Linux vsftp三种模式的简单配置部署
环境:Debian 6.1.27-1kali1 (2023-05-12) vsftpd 安装 --查看是否当前系统是否已安装 apt list --installed | grep vsftpd 没有安装的话,就正常安装 apt-get update apt-get install vsftpd 一、匿名用户模式 分享一些不重要文件,任…...

6.1.tensorRT高级(1)-概述
目录 前言1. tensorRT高级概述总结 前言 杜老师推出的 tensorRT从零起步高性能部署 课程,之前有看过一遍,但是没有做笔记,很多东西也忘了。这次重新撸一遍,顺便记记笔记。 本次课程学习 tensorRT 高级-概述 课程大纲可看下面的思维…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
