玩转LaTeX(三)【数学公式(基础)、矩阵、多行公式】
数学公式基础
导言区(引包)
\usepackage{amsmath} %带星号的eqution正文区
\begin{document}%数学公式初步\section{简介}\LaTeX{}将排版内容分为文本模式和数学模式。文本模式用于普通文本排版,数学模式用于数学公式排版。\section{行内公式} %有三种方式可以写行内公式\subsection{美元符号}交换律是 $a+b = b+a$,如$1+2=2+1=3$。\subsection{小括号}交换律是 \(a+b = b+a\),如\(1+2=2+1=3\)。\subsection{math环境}交换律是 \begin{math}a+b = b+a\end{math},如\begin{math}1+2=2+1=3\end{math}。\section{上下标}\subsection{上标}$3x^{20}-x+2 = 0$ %大括号最好都加上,无论是一位数字还是多位数字$3x^{3x^{20}-x+2}-x+2=0$ %也可以用已有的公式做上标处理不过要加大括号\subsection{下标}$a_0,a_1,a_2$$a_0,a_1,a_2,...,a_{100},a_{3x^{20}-x+2}$ %同理,超过一个数字也要加大括号,也可以代入公式\section{希腊字母}$\alpha$ \quad $\beta$ \quad$\gamma$ \quad$\epsilon$ \quad$\pi$ \quad$\omega$ \quad$\Gamma$ \quad$\Delta$ \quad$\Pi$ \quad$\Omega$ \quad %大写字母开始的希腊字母用于排版大写的希腊字母$\alpha^3+\beta^2+\gamma=0$ %希腊字母也可以用在通用公式中\section{数学函数}$\log$ \quad $\sin$ \quad$\cos$ \quad$\arcsin$ \quad$\arccos$ \quad$\ln$$\sin^2 x + \cos^2 x = 1$ %构成公式$y = \sin^{-1} x$ \quad $y = \log_2 x$ \quad $y = \ln x$$\sqrt{2}$ \quad $\sqrt{x^2+y^2}$ \quad $\sqrt{2+\sqrt{2}}$ \quad $\sqrt[4]{x}$ \quad %用于排版公式,"[]"用于指定开方次数\section{分式} %两种方式大约是原体积的$3/4$。大约是原体积的$\frac{3}{4}$。%第一个{}是分子,第二个是分母。$\frac{x}{x^2+x+1}$ %复杂公式$\frac{\sqrt{x-1}}{\sqrt{x+1}}$$\frac{1}{1+\frac{1}{x}}$$\sqrt{\frac{x}{x^2+x+1}}$\section{行间公式}\subsection{美元符号}交换律是$$a+b = b+a$$如$$1+2=2+1=3$$\subsection{中括号}交换律是\[a+b = b+a\]如\[1+2=2+1=3\]\subsection{displaymath环境}交换律是\begin{displaymath}a+b=b+a,\end{displaymath}如\begin{displaymath}1+2=2+1=3.\end{displaymath}\subsection{自动编号公式equation环境}交换律公式见式\ref{eq:commutative}\begin{equation}a+b=b+a \label{eq:commutative}\end{equation}\subsection{不编号公式equation*环境}交换律公式见式\ref{eq:commutative2} %此时的编号为小节编号\begin{equation*} %带星号的quation需要引入宏包:“\usepackage{amsmath}”a+b=b+a \label{eq:commutative2}\end{equation*}公式的编号与交叉引用也是自动实现的,大家在排版中要习惯采用自动化的方式处理诸如图、表、公式的编号与交叉引用。再如公式\ref{eq:pol}:\begin{equation}x^5-7x^3+4x = 0 \label{eq:pol}\end{equation}\end{document}

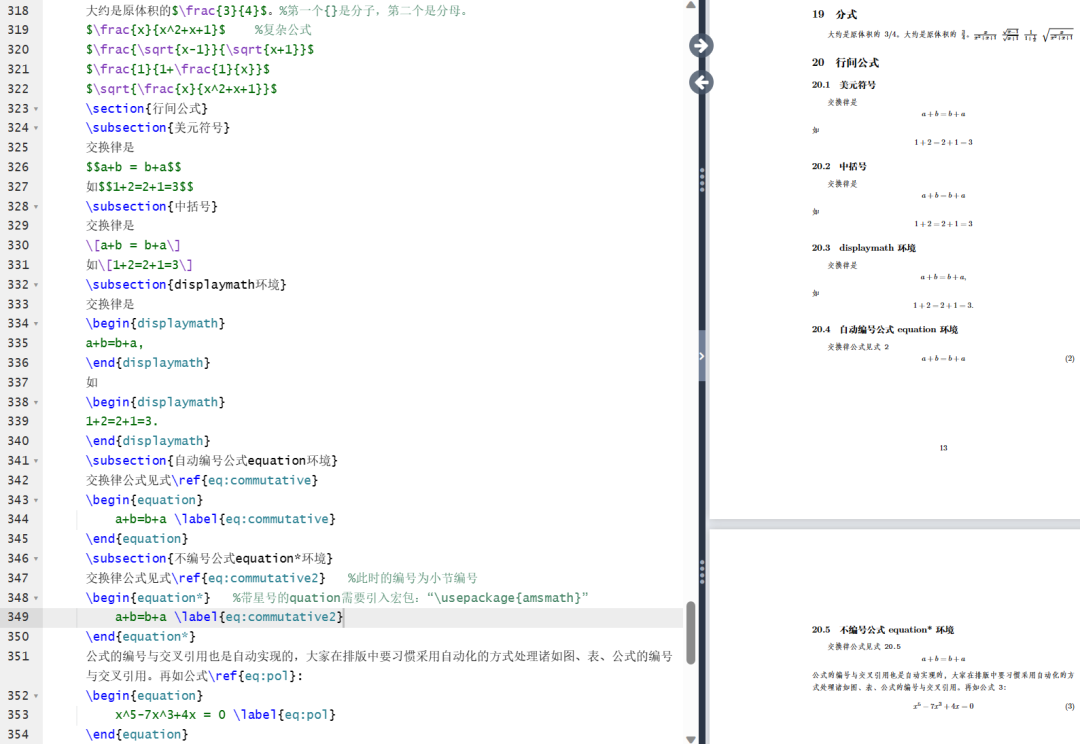
矩阵:
导言区:(自命令)
\newcommand{\adots}{\mathinner{\mkern2mu%\raisebox{0.1em}{.}\mkern2mu\raisebox{0.4em}{.}%\mkern2mu\raisebox{0.7em}{.}\mkern1mu}} %adots执行后面大括号的内容。用不同的方式排版不同的句号
正文区:
\begin{document}%矩阵%在latex中使用matrix环境实现矩阵排版,需要引入amsmath宏包\[\begin{matrix} %使用矩阵排版的matrix和使用表格排版的tabular非常相似0 & 1 \\ %用&分割列,用\\分割行1 & 0\end{matrix} \quad%pmatrix环境(矩阵两端加小括号)\begin{pmatrix}0 & -i \\i & 0\end{pmatrix} \quad\begin{bmatrix} %加中括号0 & -1 \\1 & 0\end{bmatrix} \quad\begin{Bmatrix} %加大括号1 & 0 \\0 & -1\end{Bmatrix} \quad\begin{vmatrix} %加单竖线a & b \\c & d\end{vmatrix} \quad\begin{Vmatrix} %加双竖线i & 0 \\0 & -i\end{Vmatrix} \quad\]\[A = \begin{pmatrix}a_{11}^2 & a_{12}^2 &a_{13}^2 \\ %上下标在矩阵中的使用0 & a_{22} & a_{23} \\0 & 0 & a_{33}\end{pmatrix}\]\[B = \begin{bmatrix} %矩阵中常用的省略号(横竖斜)a_{11} & \dots & a_{1n} \\\adots & \ddots & \vdots \\ %adots是自己定义出来的。当然往左斜这个省略号也可以直接用命令“\iddots”实现,不过需要导包mathdots,具体内容可见往期回顾的第一篇内容。0 & & a_{nn}\end{bmatrix}_{n \times n} %times排版乘号\]%利用矩阵的嵌套还可以实现分块矩阵 ↓↓↓\[\begin{pmatrix}\begin{matrix} 1 & 0 \\ 0 & 1\end{matrix}& \text{\Large 0} \\ %"\text{\Large 0}"表示临时切换到文本模式{\Large 0} & \begin{matrix}1 & 0 \\ 0 & -1 \end{matrix} %不加text输出的0是不一样的\end{pmatrix}\]%三角矩阵\[\begin{pmatrix}a_{11} & a_{12} \cdots & a_{1n} \\& a_{22} & \cdots & a_{2n} \\& & \ddots & \vdots \\\multicolumn{2}{c}{\raisebox{1.3ex}[0pt]{\Huge 0}}& & a_{nn} %"\multicolumn":合并多列;"\raisebox":调整高度\end{pmatrix}\]%产生跨列的省略号:\hdotsfor{<列数>}\[\begin{pmatrix}1 & \frac 12 & \dots & \frac 1n \\\hdotsfor{4} \\m & \frac m2 & \dots & \frac mn\end{pmatrix}\]%行内小矩阵(smallmatrix)环境复数 $z=(x,y)$ 也可用矩阵\begin{math}\left( %math环境下的括号手动加,也可以改成中括号等\begin{smallmatrix}x & -y \\ y & x\end{smallmatrix}\right)\end{math}来表示。%“\left”"\right"命令成对出现%array环境(类似于表格环境tabular)\[%第一行第1列\begin{array}{r|r}\frac12 & 0 \\\hline0 & -\frac abc \\ %frac命令,后面直接跟数字表示分子分母,多位数需要加花括号,frac后面不能直接跟字母,会报错,这些细节要注意。必要时用花括号进行分组,比如这里的c既不属于分母也不属于分子。\end{array}\]%利用array环境构造复杂矩阵\[\begin{array}{c@{\hspace{-5pt}}l} %@{<内容>}:添加任意内容,不占表项计数;向左移-5pt的距离\left(\begin{array}{ccc|ccc}a & \cdots & a & b & \cdots & b \\& \ddots & \vdots & \vdots & \adots \\& & a & b \\ \hline& & & c & \cdots & c \\& & & \vdots & & \vdots \\\multicolumn{3}{c|}{\raisebox{2ex}[0pt]{\Huge 0}}& c & \cdots & c\end{array}\right)&%第一行第2列\begin{array}{l}\left.\rule{0mm}{7mm}\right\}p \\ %"\left."表示与"\right\"配对,\left.什么都不输出\\\left.\rule{0mm}{7mm}\right\}q\end{array}\\[-5pt]%第二行第一列\begin{array}{cc}\underbrace{\rule{17mm}{0mm}}_m & %产生下面的横向大括号,rule指定尺寸\underbrace{\rule{17mm}{0mm}}_m\end{array}& %第二行第二列\end{array}\]\end{document}


多行公式
导言区(导包):
\usepackage{amsmath} %带星号的eqution\usepackage{amssymb}
正文区
\begin{document}%多行公式%gather环境\begin{gather} %实现对公示的分行排列及编号a + b = b + a \\ab ba\end{gather}\begin{gather*} %不带编号3 + 5 = 5 + 3 = 8 \\3 \times 5 = 5 \times 3\end{gather*}\begin{gather}3^2+4^2=5^2 \notag \\ %在gather环境中,也可以使用\notag阻止编号(“\\”前使用)5^2+12^2=13^2 \notag \\a^2+b^2=c^2\end{gather}%align环境(用&进行对齐)\begin{align}x &= t+\cos t +1\\y&==2\sin t\end{align}\begin{align*}x &= t & x &= \cos t & x &= t \\y &= 2t & y &= \sin(t+1) & y &= \sin t\end{align*}%split环境(用&对齐,跟align一样,编号在中间位置)\begin{equation}\begin{split}\cos 2x &= \cos^2 x -\sin^2 x \\&= 2\cos^2 x-1\end{split}\end{equation}%case环境(每行公式中使用&分隔两部分,通常表示值和后面的条件)【分段公式】\begin{equation}D(x) = \begin{cases}1,&\text{如果 } x\in \mathbb{Q};\\ %"\in"命令表示输出“∈”符号;“\text”命令表示临时切换到文本模式,若果不使用该命令,则在数学排版公式中无法实现中文排版。0,&\text{如果 } x\in \mathbb{R}\setminus\mathbb{Q}. %“mathbb”表示输出花体字符,需要导包:“\usepackage{amssymb}”;“\setminus”:除号\end{cases}\end{equation}\end{document}
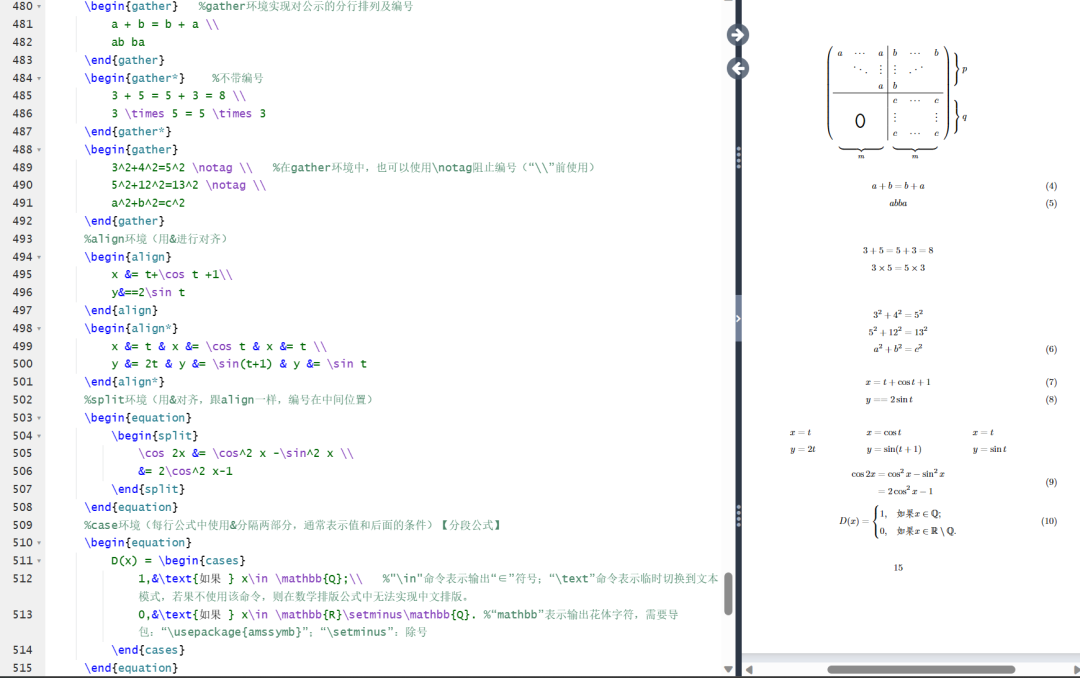
相关文章:

玩转LaTeX(三)【数学公式(基础)、矩阵、多行公式】
数学公式基础 导言区(引包) \usepackage{amsmath} %带星号的eqution 正文区 \begin{document}%数学公式初步 \section{简介} \LaTeX{}将排版内容分为文本模式和数学模式。文本模式用于普通文本排版,数学模式用于数学公式排版。 …...
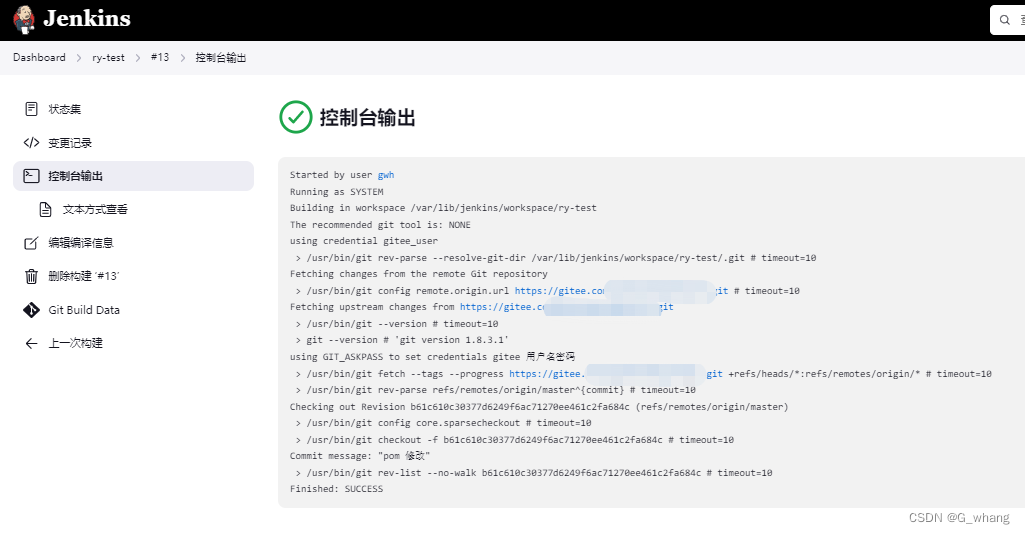
jenkins 配置git
在linux 中输入 保证git 安装成功 git --version使用查看git 安装目录(非源码安装直接用yum 安装的) which gitjenkins 中到 系统管理–>全局工具配置–> Git installations 新建一个项目 选择自由风格 源码管理选择 git 如果使用的是码云&a…...

单机部署MinIo并设置开机自启
MinIO 是高性能的对象存储,是为海量数据存储、人工智能、大数据分析而设计的,它完全兼容Amazon S3接口,单个对象最大可达5TB,适合存储海量图片、视频、日志文件、备份数据和容器/虚拟机镜像等。MinIO主要采用Golang语言实现&#…...
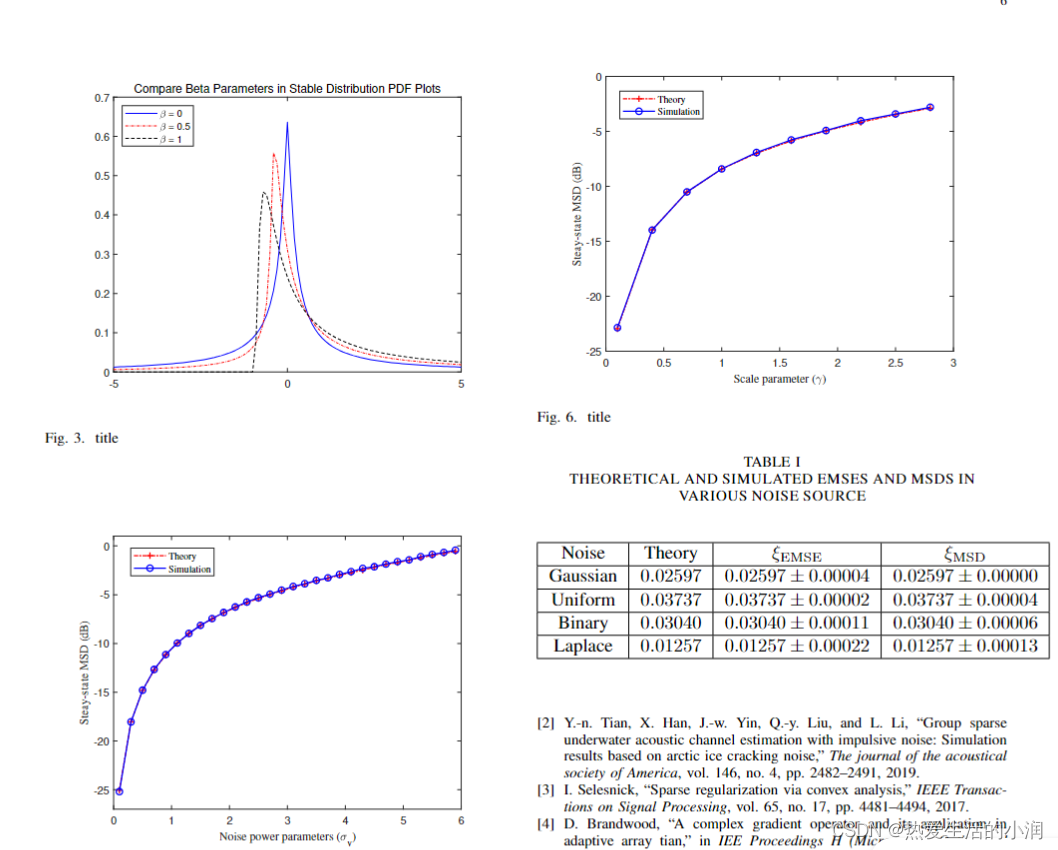
Latex | 使用MATLAB生成.eps矢量图并导入Latex中的方法
一、问题描述 用Latex时写paper时,要导入MATLAB生成的图进去 二、解决思路 (1)在MATLAB生成图片的窗口中,导出.eps矢量图 (2)把图上传到overleaf的目录 (3)在文中添加相应代码 三…...

宝塔面板定时任务重启各种服务
一个php项目,laravel框架,使用了nginx php redis mysql 还有进程守护supervisor,用于laravel的异步队列进程queue,当服务器重启后有可能部分服务没有成功启动这个时候可以用定时任务去检查服务状态,然后对不正常的自动…...

Ansible playbook编写
目录 palybooks 组成示例:运行palybook定义,引用变量when 条件判断循环Templates模块tags 模块 palybooks 组成 Tasks:任务,即通过 task 调用 ansible 的模板将多个操作组织在一个 playbook 中运行Variables:变量Temp…...

个人博客系统 -- 登录页面添加图片验证码
目录 1. 功能展示 2. 前段代码 3. 后端代码 1. 功能展示 在登录页面添加验证码登录 1. 检测到没有输入验证码或者输入的验证码错误时,进行弹窗提示.并且刷新当前验证码图片 2. 点击验证码进行刷新 2. 前段代码 1. 添加验证码标签,在密码的下面,在login.html进行修改 主要…...

剑指offer10-I.斐波那契数列
学计算机的对这道题肯定不陌生,我记得是学C语言的时候学递归的时候有这道题,于是我就世界用递归写了如下代码: class Solution {public int fib(int n) {if(n1) return 1;if(n0) return 0;return (fib(n-1) fib(n-2)) % 1000000007;} } 到…...
13年测试经验,性能测试-压力测试指标分析总结,看这篇就够了...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 一般推荐…...

大数据课程D3——hadoop的Source
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 掌握Source的AVRO Source; ⚪ 掌握Source的Exec Source; ⚪ 掌握Source的Spooling Directory Source; ⚪ 掌握Source的Netcat Source; ⚪ 掌握Source的Sequence Generator Source;…...
F5 LTM 知识点和实验 4-持久化
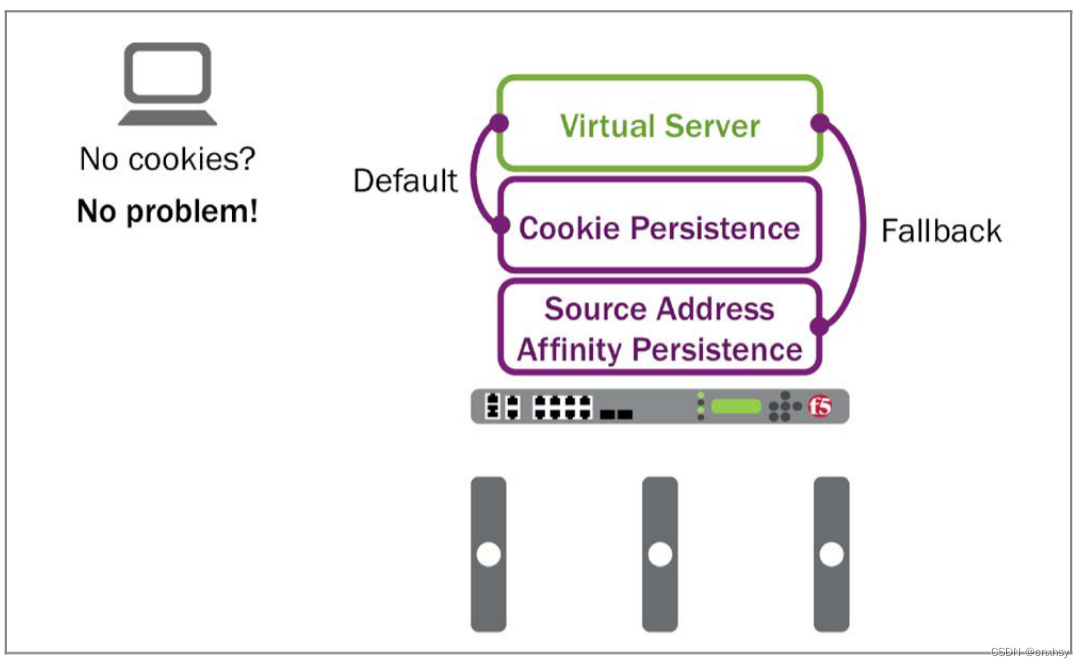
第四章:持久化 持久化: 大多数应用都是有状态的,比如,使用一个购物网站,最重要的是用户在放入一个商品之后,刷新网页要能继续看到购物车里的东西,这就需要请求报文发到同一个后端服务器上,持久化就能完成这个功能。 持久化支持一下几种场景: 源地址目标地址SSLSIPH…...

SpringBoot之WebMvcConfigurer详解
目录 一、基本介绍 二、WebMvcConfigurer接口展示 三、常用方法列举 3.1 addInterceptors:添加拦截器 3.2 addResourceHandlers:添加静态资源 3.3 addCorsMappings:添加跨域 编写的初衷是为了自己巩固复习,如果能帮到你将是…...

WPF实战学习笔记22-添加自定义询问窗口
添加自定义询问窗口 详细代码:https://github.com/DongLiqiang/Mytodo/commit/221de6b2344d5c861f1d3b2fbb2480e3e3b35c26 添加自定义询问窗口显示方法 修改文件Mytodo.Extensions.DialogExtension 添加内容,类中添加内容 /// <summary> /// …...

Spring Boot项目的创建
hi 大家好,又见面了,今天继续讲解Spring Boot 文章目录 🐶1.什么是Spring Boot?🐶2.Spring Boot的优势🐶3.Spring Boot项目创建🌼3.1使用ieda创建🥝3.1.1下载插件Spring Boot Helper🥝3.1.2创建项目 &…...

Python加载数据的5种方法
大家好,今天回顾五种引入数据的Python技术,并附有代码实例参考。 我们将使用Numpy、Pandas和Pickle包,所以要导入它们: import numpy as np import pandas as pd import pickle Manual功能 这是最困难的,因为你必须…...
QPoint、QLine、QSize、QRect
QPoint、QLine、QSize、QRect QPointQLineQSizeQRect QPoint // 构造函数 // 构造一个坐标原点, 即(0, 0) QPoint::QPoint(); // 参数为 x轴坐标, y轴坐标 QPoint::QPoint(int xpos, int ypos);// 设置x轴坐标 void QPoint::setX(int x); // 设置y轴坐标 void QPoint::setY(in…...
vue+leaflet笔记之地图量测
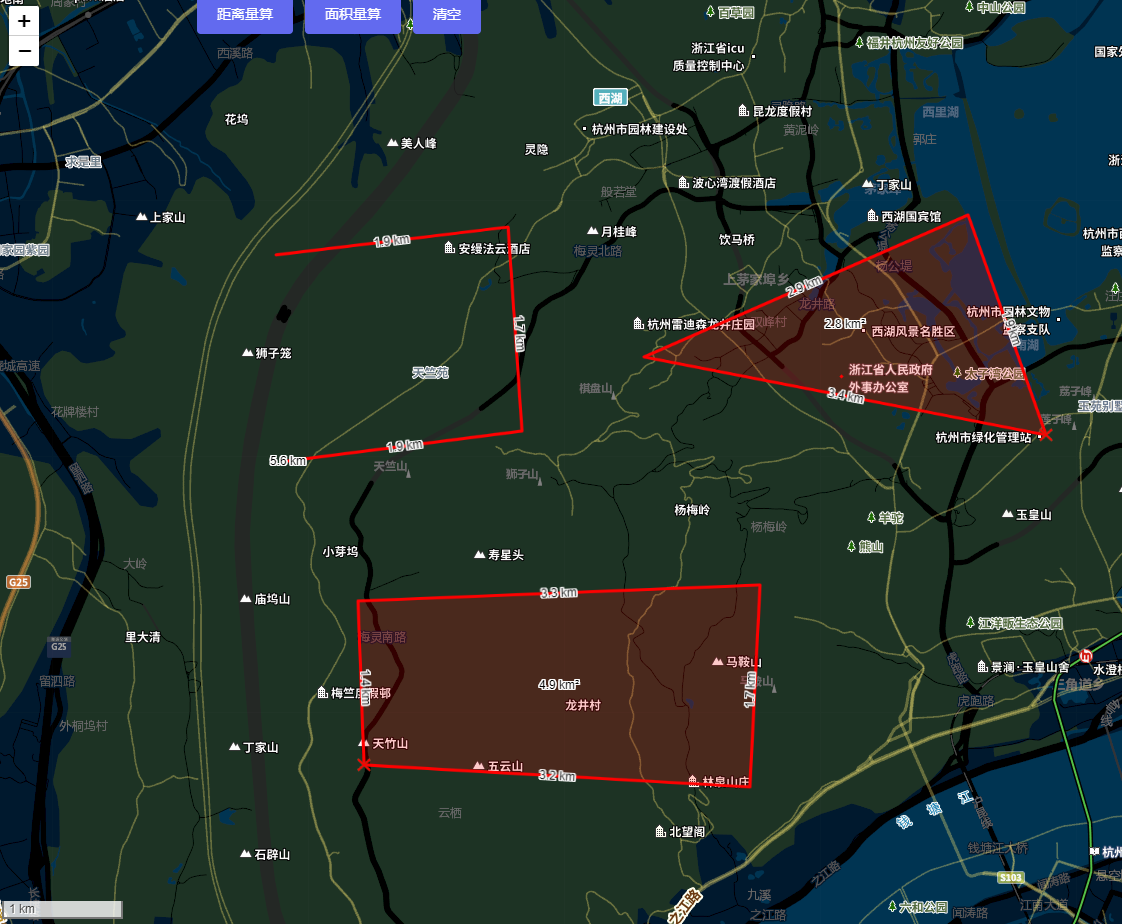
vueleaflet笔记之地图量测 文章目录 vueleaflet笔记之地图量测开发环境代码简介插件简介与安装使用简介图形量测动态量测 详细源码(Vue3) 本文介绍了Web端使用Leaflet开发库进行距离量测的一种方法 (底图来源:天地图),结合leaflet-measure-path插件能够快速的实现地…...

“深入理解SpringBoot:从入门到精通的几个关键要点“
标题:深入理解Spring Boot:从入门到精通 摘要:本文将深入探讨Spring Boot的关键要点,帮助读者从入门到精通。我们将从Spring Boot的基本概念开始,介绍自动配置、起步依赖、注解驱动开发等特性,并通过示例代…...
数值线性代数: 共轭梯度法
本文总结线性方程组求解的相关算法,特别是共轭梯度法的原理及流程。 零、预修 0.1 LU分解 设,若对于,均有,则存在下三角矩阵和上三角矩阵,使得。 设,若对于,均有,则存在唯一的下三…...
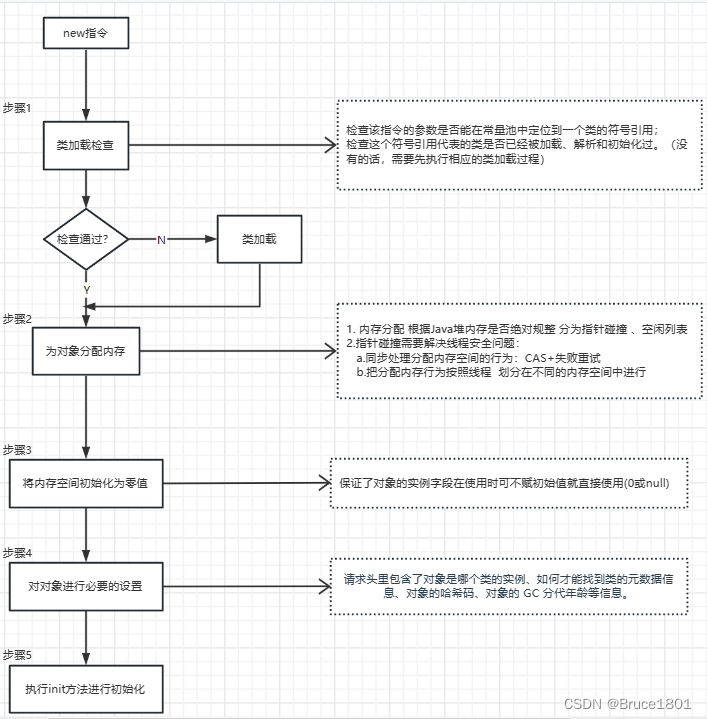
【JVM】详解对象的创建过程
文章目录 1、创建对像的几种方式1、new关键字2、反射3、clone4、反序列化 2、创建过程步骤 1、检查类是否已经被加载步骤 2、 为对象分配内存空间1、指针碰撞针对指针碰撞线程不安全,有两种方案: 2、空闲列表选择哪种分配方式 步骤3、将内存空间初始化为…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...

Python环境安装与虚拟环境配置详解
本文档旨在为Python开发者提供一站式的环境安装与虚拟环境配置指南,适用于Windows、macOS和Linux系统。无论你是初学者还是有经验的开发者,都能在此找到适合自己的环境搭建方法和常见问题的解决方案。 快速开始 一分钟快速安装与虚拟环境配置 # macOS/…...
