matlab进阶:求解在约束条件下的多元目标函数最值(fmincon函数详解)
🌅*🔹** φ(゜▽゜*)♪ **🔹*🌅
欢迎来到馒头侠的博客,该类目主要讲数学建模的知识,大家一起学习,联系最后的横幅!喜欢的朋友可以关注下,私信下次更新不迷路!
资源链接:点击这里获取众多源码、数模资料、思路精讲、论文模板latex和word、学习书籍等
文章目录
- 💧 fmincon函数说明
- 目标优化问题的基本形式
- fmincon语法和参数
- 💧 算例实战
- 初始解x0的设定
- 线性等式和不等式约束
- 非线性等式和不等式约束
- 含有求和公式目标函数
💧 fmincon函数说明
Matlab 的 fmincon 函数:寻找约束非线性多变量函数的最小值。
适用于:
- 线性函数
- 非线性函数
- 线性等式和不等式约束
- 非线性等式和不等式约束
目标优化问题的基本形式
min f ( x ) \min f(x) minf(x)
s . t . { A ⋅ x ≤ b A e q ⋅ x = B e q l b ≤ x ≤ u b c ( x ) ≤ 0 c e q ( x ) = 0 s.t. \begin{cases} A \cdot x \leq b \\ Aeq \cdot x = Beq \\ lb \leq x \leq ub \\ c(x) \leq 0 \\ ceq(x) = 0 \end{cases} s.t.⎩ ⎨ ⎧A⋅x≤bAeq⋅x=Beqlb≤x≤ubc(x)≤0ceq(x)=0
fmincon语法和参数
[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
输入参数:
- fun :目标函数,注意需要单引号,或者@,(即写为符号函数)
- x0:函数fun参数值的初始化;
- A, b:参数值的线性不等式约束(A * x <= b)
- Aeq, beq:参数值的等式线性约束 (Aeq * x = beq)
- lb, ub:参数值的下界和上界
- options:使用所指定的优化选项执行,options 可设置这些选项
- nonlcon:非线性约束,其参数值一般为约束函数。如果没有非线性不等式或等式约束,设置为 nonlcon = []
输出参数:
- x:输出最优参数值
- fval:输出 fun 在X参数的值
- exitflag: 输出fmincon额外条件值
- lambda :结构体,其字段包含解 x 处的拉格朗日乘数。
- grad:fun 在解 x 处的梯度。
- hessian:fun 在解 x 处的黑塞矩阵。请参阅fmincon Hessian 矩阵。
💧 算例实战
算例都是比较简单的,希望大家好好理解,单元和多元区别不大,进阶的话重点是关于fmincon求解结果的分析,目标函数属于凸函数还是非凸,是否全局最优还是局部最优,还得考虑fmincon求解的约束容限等。
初始解x0的设定
初始解的设定也很重要,得结合你所选用的算法。下面我都是直接设定x0=rand(2,1),大家可以尝试修改初始解,看看结果有什么不同。
线性等式和不等式约束
min f ( x ) = 3 ⋅ x 1 + 5 ⋅ x 2 \min f(x)=3 \cdot x_1 +5 \cdot x_2 minf(x)=3⋅x1+5⋅x2
s . t . { x 1 + 3 x 2 ≤ 20 2 x 1 + x 2 ≤ 30 x 1 + x 2 = 10 0 ≤ x 1 ≤ 10 3 ≤ x 2 ≤ 8 s.t. \begin{cases} x_1+3 x_2 \leq 20 \\ 2 x_1+x_2 \leq 30 \\ x_1+x_2 = 10 \\ 0 \leq x_1 \leq 10 \\ 3 \leq x_2 \leq 8 \\ \end{cases} s.t.⎩ ⎨ ⎧x1+3x2≤202x1+x2≤30x1+x2=100≤x1≤103≤x2≤8
将其与前面目标规划问题的基本形式对照即可,代码如下:
clc
clear
close all
fun=@(x) 3*x(1)+ 5*x(2);
x0=rand(1,2);
A=[1,3;2,1];
b=[20;30];
Aeq=[1,1];
beq=[10];
lb=[0,3];
ub=[10,8];
[x,fval,exitflag]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
非线性等式和不等式约束
这里注意非线性部分得移项成标准形式,即非线性部分≤0和非线性部分=0的形式,下方换成上面形式得移向变号,大家看到负号别讶异。
min f ( x ) = 3 ⋅ x 1 2 + 5 ⋅ x 2 2 \min f(x)=3 \cdot x_1^2 +5 \cdot x_2^2 minf(x)=3⋅x12+5⋅x22
s . t . { x 1 + 3 x 2 ≤ 20 2 x 1 + x 2 ≤ 30 x 1 + x 2 = 10 0 ≤ x 1 ≤ 10 3 ≤ x 2 ≤ 8 x 1 2 − x 2 ≥ 0 x 1 − x 2 2 + 1 = 0 s.t. \begin{cases} x_1+3 x_2 \leq 20 \\ 2 x_1+x_2 \leq 30 \\ x_1+x_2 = 10 \\ 0 \leq x_1 \leq 10 \\ 3 \leq x_2 \leq 8 \\ x_1^2-x_2 \geq 0 \\ x_1-x_2^2 + 1 = 0 \end{cases} s.t.⎩ ⎨ ⎧x1+3x2≤202x1+x2≤30x1+x2=100≤x1≤103≤x2≤8x12−x2≥0x1−x22+1=0
主函数:
clc
clear
close all
fun=@(x) 3*x(1)^2+ 5*x(2)^2;
x0=rand(1,2);
A=[1,3;2,1];
b=[20;30];
Aeq=[1,1];
beq=[10];
lb=[0,3];
ub=[10,8];
[x,fval,exitflag]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub,'mycon')
新建mycon.m函数
function [c,ceq]=mycon(x)
c=-x(1)^2+x(2);
ceq=-x(1)-x(2)^2+1;
含有求和公式目标函数
若目标函数含有求和公式,如何用代码表示呢?
min f ( x ) = ∑ i 50 ( x i − 1 ) 2 \min f(x)= \sum_i^{50}(x_i-1)^2 minf(x)=i∑50(xi−1)2
- 其中x为自变量,c为已知量
则我们的目标函数为
function f = fun(x)
f = 0;
for i=1:50f = f + (x(i) - 1)^2
end

相关文章:

matlab进阶:求解在约束条件下的多元目标函数最值(fmincon函数详解)
🌅*🔹** φ(゜▽゜*)♪ **🔹*🌅 欢迎来到馒头侠的博客,该类目主要讲数学建模的知识,大家一起学习,联系最后的横幅! 喜欢的朋友可以关注下,私信下次更新不迷路࿰…...
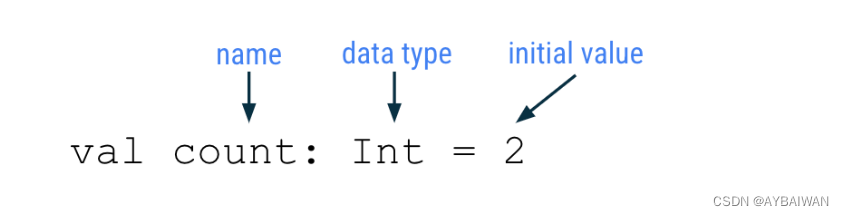
Kotlin知识点
Kotlin 是 Google 推荐的用于创建新 Android 应用的语言。使用 Kotlin,可以花更短的时间编写出更好的 Android 应用。 基础 Kotlin 程序必须具有主函数,这是 Kotlin 编译器在代码中开始编译的特定位置。主函数是程序的入口点,或者说是起点。…...
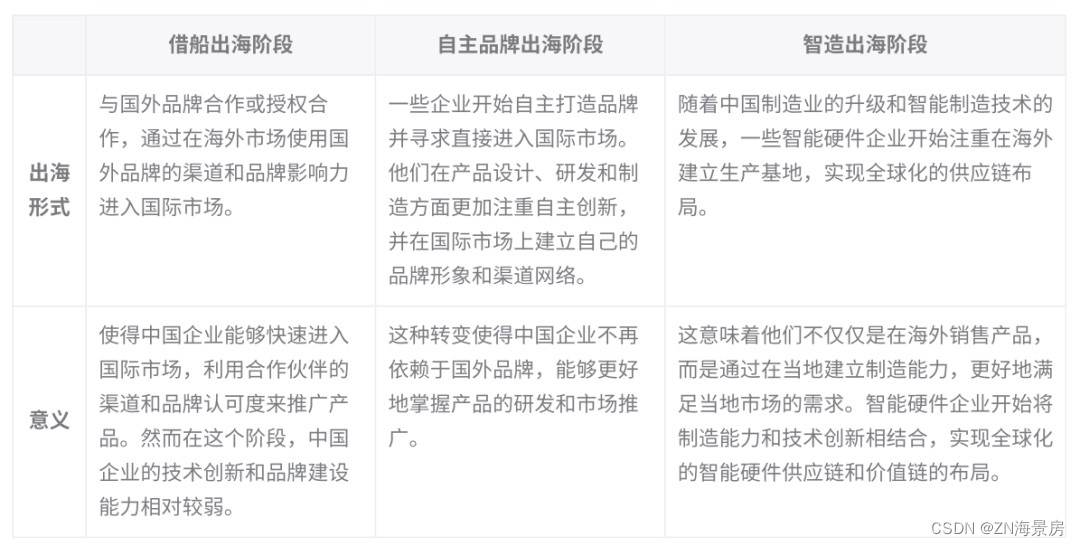
亚马逊云科技联合霞光社发布《2013~2023中国企业全球化发展报告》
中国企业正处于全球聚光灯下。当企业全球化成为时代发展下的必然趋势,出海也从“可选项”变为“必选项”。中国急速扩大的经济规模,不断升级的研发和制造能力,都在推动中国企业不断拓宽在全球各行业的疆域。 过去十年,是中国企业…...
【解析excel】利用easyexcel解析excel
【解析excel】利用easyexcel解析excel POM监听类工具类测试类部分测试结果备注其他 EasyExcel Java解析、生成Excel比较有名的框架有Apache poi、jxl。但他们都存在一个严重的问题就是非常的耗内存,poi有一套SAX模式的API可以一定程度的解决一些内存溢出的问题&…...

JQuery操作单选按钮Radio和复选框checkbox
获取选中值: $(input:radio:checked).val();$("input[typeradio]:checked").val();$("input[namerd]:checked").val();$("input[idrand_question]:checked").val();设置第一个Radio为选中值: $(input:radio:…...
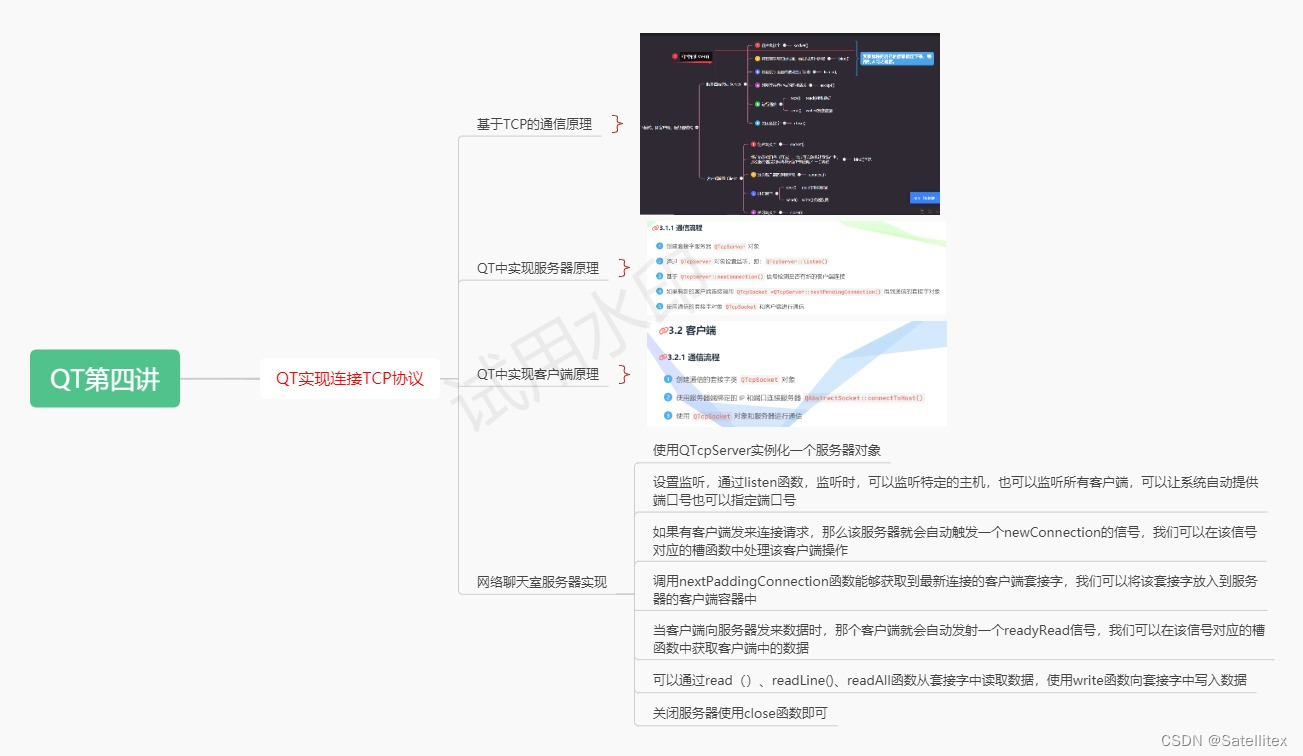
7.28 作业 QT
手动完成服务器的实现,并具体程序要注释清楚: widget.h: #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QTcpServer> //服务器类 #include <QTcpSocket> //客户端类 #include <QMessageBox> //对话框类 #include …...

HTML <pre> 标签
定义和用法 pre 元素可定义预格式化的文本。被包围在 pre 元素中的文本通常会保留空格和换行符。而文本也会呈现为等宽字体。 <pre> 标签的一个常见应用就是用来表示计算机的源代码。 可以导致段落断开的标签(例如标题、"><p> 和 标签"><a…...

查询结果元数据-MetaData对象、数据库工具类的封装、通过反射实现数据查询的封装
六、查询结果元数据-MetaData对象 七、数据库工具类的封装 1、PropertieUtil类 2、DbUtil类 3、DBHepler类 查询: 4、TestDb测试类: 更新: 1)插入: 2)修改: 3)删除: 查…...
【Minio中间件】上传图片并Vue回显
流程: 目录 1.文件服务器Minio的安装 1.1 下载Minio安装后,新建1个data文件夹。并在该安装目录cmd 敲命令。注意不要进错目录。依次输入 1.2 登录Minio网页端 1.3 先建1个桶(buckets),点击create a bucket 2. Spr…...
Jmeter配置不同业务请求比例,应对综合场景压测
需求: 每次向服务器发出请求时,先生成一个随机数,我们对随机数的取值划分若干个范围(对应若干个业务请求),然后对随机数进行判断,当随机数落在某个范围内,就可以执行对应的请求。比…...

数学分析:流形的线性代数回顾
因为是线性的,所以可以把所有的系数都提取出去。这也是多重线性代数的性质。可以看成基本的各项自变量的乘法。 这里可以看到两个不同基向量下,他们的坐标转化关系。 引出了张量积,也就是前面提到的内容。 对偶空间的例子总是比较美好。 因为…...

前端请求后端接口返回错误码
1、如果 HTTP Code 是 2xx 范围内的,那通常表明请求已经成功处理,并且可以根据具体的 HTTP Code 进一步判断请求的处理结果。比如: HTTP Code 200 表明请求成功,并返回了请求资源;HTTP Code 204 表明请求成功…...

【Java Web】Nacos 介绍和安装教程
文章目录 1. Nacos 介绍1.1 Nacos 的定义1.2 Nacos 的主要功能1.2.1 服务注册与发现1.2.2 配置管理1.2.3 动态 DNS 服务1.2.4 服务和元数据管理 1.3 Nacos 的适用场景1.3.1 微服务架构1.3.2 动态配置管理1.3.3 多环境部署1.3.4 云原生应用 2. Nacos 的核心组件2.1 服务注册与发…...

web漏洞-java安全(41)
这个重点是讲关于java的代码审计,看这些漏洞是怎么在java代码里面产生的。 #Javaweb 代码分析-目录遍历安全问题 这个漏洞原因前面文章有,这次我们看看这个漏洞如何在代码中产生的,打开靶场 解题思路就是通过文件上传,上传文件…...
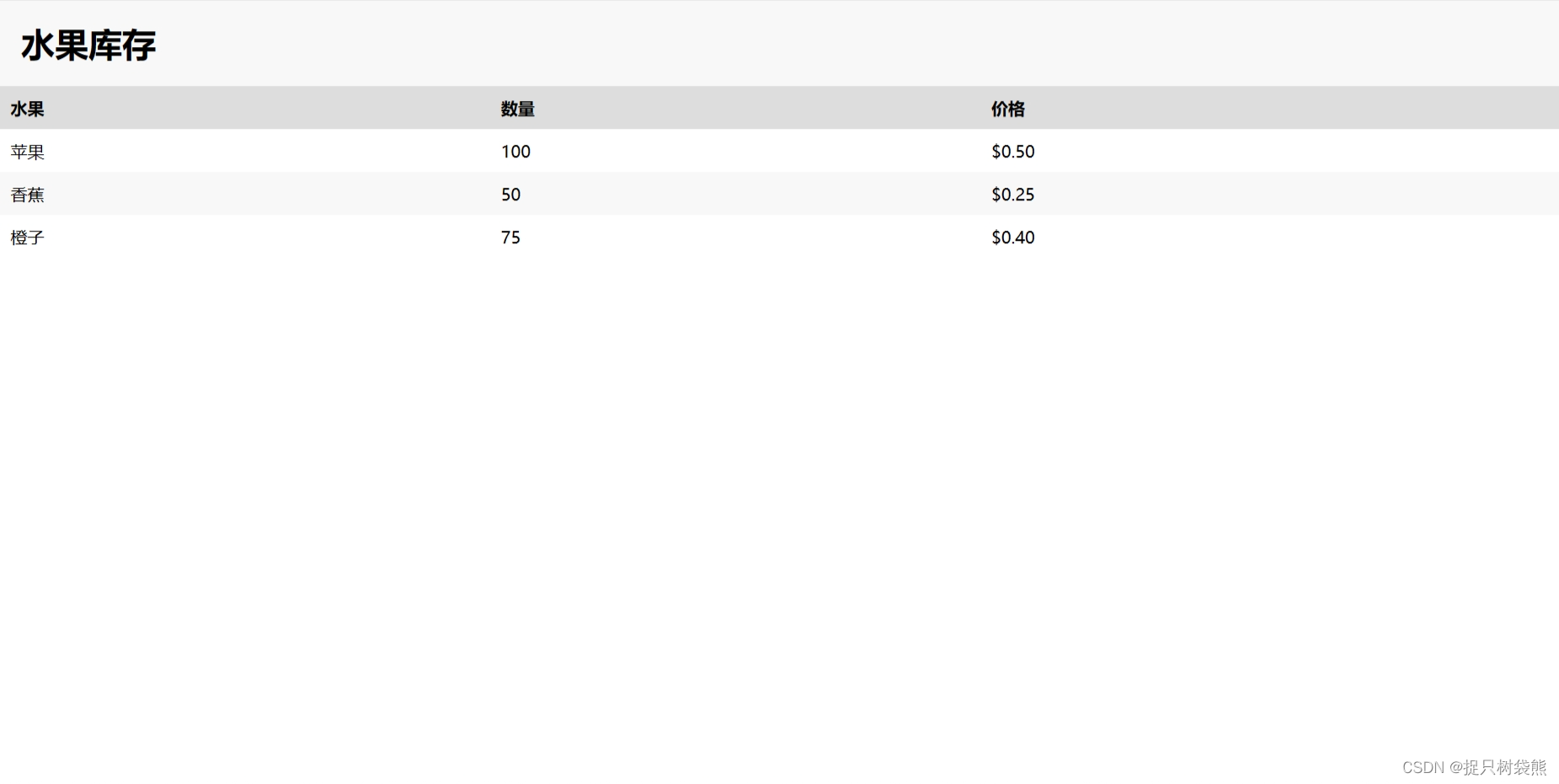
用CSS和HTML写一个水果库存静态页面
HTML代码: <!DOCTYPE html> <html> <head><link rel"stylesheet" type"text/css" href"styles.css"> </head> <body><header><h1>水果库存</h1></header><table>…...

【回眸】备考PMP考点汇总 三(距离考试还有20天)
目录 前言 【回眸】备考PMP考点汇总 三(距离考试还有20天) 29、管理质量 30、获取资源 31、建设团队 32、管理团队 33、管理沟通 34、实施风险应对 35、实施采购 36、管理相关方参与 37、监控项目工作(10%) 38、实施整…...

新房的收房验房注意事项
文章目录 流程注意事项准备检查材料手续整体结构验收水电检测门窗结构地面工程墙面工程顶面工程阳台厨房卫生间户外设施 流程注意事项 只要发现问题,不管大小,都要在相关文件或表格中记录下来,而不管开发商以及陪同的收房人员如何花言巧语。…...
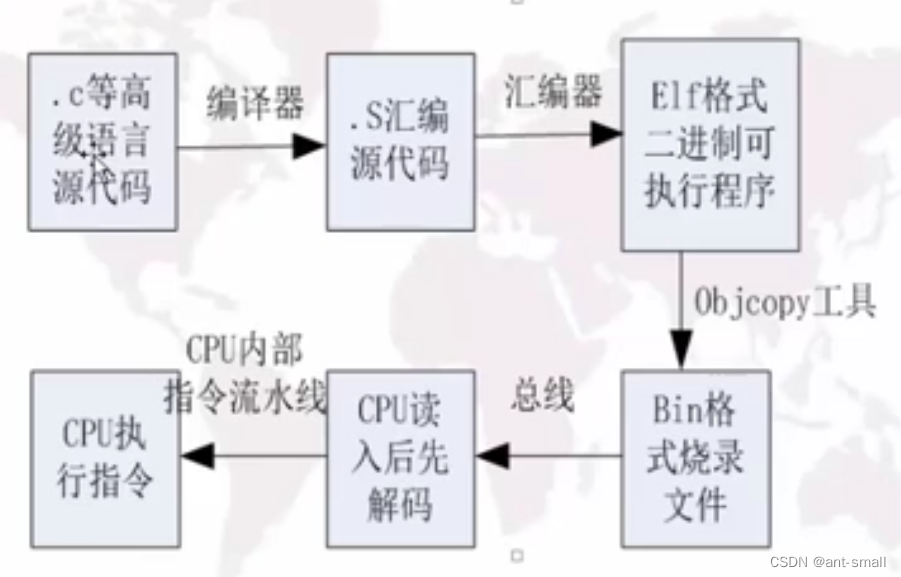
ARM裸机-5
1、可编程器件的编程原理 1.1、电子器件的发展方向 模拟器件-->数字器件 ASIC-->可编程器件 1.2、可编程器件的特点 CPU在固定频率的时钟控制下节奏运行。 CPU可以通过总线读取外部存储设备中的二进制指令集,然后解码执行。 这些可以被CPU解码执行的二进制指…...
——分布式搜索ElasticSeach场景使用)
SpringCloud学习路线(11)——分布式搜索ElasticSeach场景使用
一、DSL查询文档 (一)DSL查询分类 ES提供了基于JSON的DSL来定义查询。 1、常见查询类型: 查询所有: 查询出所有的数据,例如,match_all全文检索(full text)查询: 利用…...

负数补码表示
负数补码作用 在计算机中加法和减法采用同一电路,即用加法表示减法,如7 - 2 5变成7 ( -2) 5,这样减法的电路不用另行设计,但计算机中数据以二进制存储,没有负号,因此设计负数补码代…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...
