【机器学习】Multiple Variable Linear Regression

首先，导入所需的库

import copy, math
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('./deeplearning.mplstyle')
np.set_printoptions(precision=2)  # reduced display precision on numpy arrays

1、问题描述

使用房价预测的示例来构建线性回归模型。训练数据集包含三个样本，每个样本有四个特征（面积、卧室数、楼层数和年龄），如下表所示。这里的面积以平方英尺（sqft）为单位。

Size (sqft)	Number of Bedrooms	Number of floors	Age of Home	Price (1000s dollars)
2104	5	1	45	460
1416	3	2	40	232
852	2	1	35	178

使用这些值构建线性回归模型，从而可以预测其他房屋的价格。例如，给定一个1200平方英尺、3个卧室、1层楼、40岁的房屋，可以用模型来预测其价格。

根据表格数据创建 X_train 和 y_train 变量。

X_train = np.array([[2104, 5, 1, 45], [1416, 3, 2, 40], [852, 2, 1, 35]])
y_train = np.array([460, 232, 178])

1.1 包含样例的X矩阵

与上面的表格类似，样例被存储在一个 NumPy 矩阵X_train 中。矩阵中的每一行表示一个样例。当有 $m$ 个训练样例，每个样例有 $n$ 个特征时，$\mathbf{X}$ 是一个维度为 ($m$, $n$) 的矩阵（m 行，n 列）。

$$\mathbf{X}=\left(\begin{array}{cccc}{x}_0^{(0)}& x_1^{(0)}& \cdots & x_{n-1}^{(0)}\\ x_0^{(1)}& x_1^{(1)}& \cdots & x_{n-1}^{(1)}\\ \cdots & & & \\ x_0^{(m-1)}& x_1^{(m-1)}& \cdots & x_{n-1}^{(m-1)}\end{array}\right)$$

notation:

• ${\mathbf{x}}^{(i)}$ 是包含第 i 个样例的向量。 ${\mathbf{x}}^{(i)}=(x_0^{(i)},x_1^{(i)},\cdots ,x_{n-1}^{(i)})$
• $x_j^{(i)}$ 是第 i 个样例中的第 j 个元素。圆括号中的上标表示样例编号，而下标表示元素编号。

# data is stored in numpy array/matrix
print(f"X Shape: {X_train.shape}, X Type:{type(X_train)})")
print(X_train)
print(f"y Shape: {y_train.shape}, y Type:{type(y_train)})")
print(y_train)

1.2 参数向量 w, b

• $\mathbf{w}$ 是具有 $n$ 个元素的向量
  • 每个元素包含一个特征相关的参数
  • i在我们的数据集中, n = 4.
  • 将这表示为列向量

$$\mathbf{w}=\left(\begin{array}{c}{w}_0\\ w_1\\ \cdots \\ w_{n-1}\end{array}\right)$$

• $b$ 是一个标量参数

为了演示，$\mathbf{w}$ 和 $b$ 将被加载为一些初始选定的值，这些值接近最优解。$\mathbf{w}$ 是一个一维的 NumPy 向量。

b_init = 785.1811367994083
w_init = np.array([ 0.39133535, 18.75376741, -53.36032453, -26.42131618])
print(f"w_init shape: {w_init.shape}, b_init type: {type(b_init)}")

2、多变量的模型预测

多变量的线性回归模型的预测可以表示为：
$$f_{\mathbf{w},b}(\mathbf{x})=w_0{x}_0+w_1{x}_1+...+w_{n-1}{x}_{n-1}+b\text{\hspace{1em}(1)}$$
或用向量表示:
$$f_{\mathbf{w},b}(\mathbf{x})=\mathbf{w}\cdot \mathbf{x}+b\text{\hspace{1em}(2)}$$
其中 $\cdot$ 是向量点积

2.1 逐元素进行预测

之前的预测是将一个特征值乘以一个参数，然后再加上一个偏置参数。将之前的预测直接扩展到多个特征的实现，可以通过循环遍历每个元素，在每个元素上进行乘法操作，然后在最后加上偏置参数来实现。

def predict_single_loop(x, w, b): """single predict using linear regressionArgs:x (ndarray): Shape (n,) example with multiple featuresw (ndarray): Shape (n,) model parameters    b (scalar):  model parameter     Returns:p (scalar):  prediction"""n = x.shape[0]p = 0for i in range(n):p_i = x[i] * w[i]  p = p + p_i         p = p + b                return p

# get a row from our training data
x_vec = X_train[0,:]
print(f"x_vec shape {x_vec.shape}, x_vec value: {x_vec}")# make a prediction
f_wb = predict_single_loop(x_vec, w_init, b_init)
print(f"f_wb shape {f_wb.shape}, prediction: {f_wb}")

x_vec. 是一个具有四个元素的 1-D NumPy 向量， f_wb 是一个标量。

2.2 向量点积进行预测

使用NumPy的 np.dot() 对向量进行点积操作，加快预测速度。

def predict(x, w, b): """single predict using linear regressionArgs:x (ndarray): Shape (n,) example with multiple featuresw (ndarray): Shape (n,) model parameters   b (scalar):             model parameter Returns:p (scalar):  prediction"""p = np.dot(x, w) + b     return p    

# get a row from our training data
x_vec = X_train[0,:]
print(f"x_vec shape {x_vec.shape}, x_vec value: {x_vec}")# make a prediction
f_wb = predict(x_vec,w_init, b_init)
print(f"f_wb shape {f_wb.shape}, prediction: {f_wb}")

运行后可以看到，向量点积和元素循环的结果是相同的。

3、多变量线性回归模型计算损失

多变量线性回归的损失函数 $J(\mathbf{w},b)$ 方程如下:
$$J(\mathbf{w},b)=\frac{1}{2m}\sum _{i=0}^{m-1}(f_{\mathbf{w},b}({\mathbf{x}}^{(i)})-y^{(i)}{)}^2\text{\hspace{1em}(3)}$$
其中:
$$f_{\mathbf{w},b}({\mathbf{x}}^{(i)})=\mathbf{w}\cdot {\mathbf{x}}^{(i)}+b\text{\hspace{1em}(4)}$$

$\mathbf{w}$ 和 ${\mathbf{x}}^{(i)}$ 是向量。

具体实现如下：

def compute_cost(X, y, w, b): """compute costArgs:X (ndarray (m,n)): Data, m examples with n featuresy (ndarray (m,)) : target valuesw (ndarray (n,)) : model parameters  b (scalar)       : model parameterReturns:cost (scalar): cost"""m = X.shape[0]cost = 0.0for i in range(m):                                f_wb_i = np.dot(X[i], w) + b           #(n,)(n,) = scalar (see np.dot)cost = cost + (f_wb_i - y[i])**2       #scalarcost = cost / (2 * m)                      #scalar    return cost

# Compute and display cost using our pre-chosen optimal parameters. 
cost = compute_cost(X_train, y_train, w_init, b_init)
print(f'Cost at optimal w : {cost}')

4、多变量线性回归模型梯度下降

多变量线性回归的梯度下降方程如下:

repeat until convergence: { w j = w j − α ∂ J ( w , b ) ∂ w j for j = 0..n-1 b = b − α ∂ J ( w , b ) ∂ b } \begin{align*} \text{repeat}&\text{ until convergence:} \; \lbrace \newline\; & w_j = w_j - \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \tag{5} \; & \text{for j = 0..n-1}\newline &b\ \ = b - \alpha \frac{\partial J(\mathbf{w},b)}{\partial b} \newline \rbrace \end{align*} repeat}​ until convergence:{wj​=wj​−α∂wj​∂J(w,b)​b  =b−α∂b∂J(w,b)​​for j = 0..n-1(5)​

其中，n是特征的数量,参数 $w_j$, $b$, 同时更新

$$\begin{array}{rl}\frac{\partial J(\mathbf{w},b)}{\partial w_j}& =\frac{1}{m}\sum _{i=0}^{m-1}(f_{\mathbf{w},b}({\mathbf{x}}^{(i)})-y^{(i)})x_j^{(i)}\\ \frac{\partial J(\mathbf{w},b)}{\partial b}& =\frac{1}{m}\sum _{i=0}^{m-1}(f_{\mathbf{w},b}({\mathbf{x}}^{(i)})-y^{(i)})\end{array}\text{\hspace{1em}(6)(7)}$$

• m 是训练数据集样例的个数

• $f_{\mathbf{w},b}({\mathbf{x}}^{(i)})$ 是模型的预测值, $y^{(i)}$ 是目标值。

4.1 计算梯度

下面是方程(6)和(7)的实现

• 外循环m个样例.
  • 对每个样例计算并累加 $\frac{\partial J(\mathbf{w},b)}{\partial b}$
  • 内循环n个特征:
    • 对于每个 $w_j$计算 $\frac{\partial J(\mathbf{w},b)}{\partial w_j}$

def compute_gradient(X, y, w, b): """Computes the gradient for linear regression Args:X (ndarray (m,n)): Data, m examples with n featuresy (ndarray (m,)) : target valuesw (ndarray (n,)) : model parameters  b (scalar)       : model parameterReturns:dj_dw (ndarray (n,)): The gradient of the cost w.r.t. the parameters w. dj_db (scalar):       The gradient of the cost w.r.t. the parameter b. """m,n = X.shape           #(number of examples, number of features)dj_dw = np.zeros((n,))dj_db = 0.for i in range(m):                             err = (np.dot(X[i], w) + b) - y[i]   for j in range(n):                         dj_dw[j] = dj_dw[j] + err * X[i, j]    dj_db = dj_db + err                        dj_dw = dj_dw / m                                dj_db = dj_db / m                                return dj_db, dj_dw

#Compute and display gradient 
tmp_dj_db, tmp_dj_dw = compute_gradient(X_train, y_train, w_init, b_init)
print(f'dj_db at initial w,b: {tmp_dj_db}')
print(f'dj_dw at initial w,b: \n {tmp_dj_dw}')

4.2梯度下降

下面是方程(5)的实现

def gradient_descent(X, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters): """Performs batch gradient descent to learn theta. Updates theta by taking num_iters gradient steps with learning rate alphaArgs:X (ndarray (m,n))   : Data, m examples with n featuresy (ndarray (m,))    : target valuesw_in (ndarray (n,)) : initial model parameters  b_in (scalar)       : initial model parametercost_function       : function to compute costgradient_function   : function to compute the gradientalpha (float)       : Learning ratenum_iters (int)     : number of iterations to run gradient descentReturns:w (ndarray (n,)) : Updated values of parameters b (scalar)       : Updated value of parameter """# An array to store cost J and w's at each iteration primarily for graphing laterJ_history = []w = copy.deepcopy(w_in)  #avoid modifying global w within functionb = b_infor i in range(num_iters):# Calculate the gradient and update the parametersdj_db,dj_dw = gradient_function(X, y, w, b)   ##None# Update Parameters using w, b, alpha and gradientw = w - alpha * dj_dw               ##Noneb = b - alpha * dj_db               ##None# Save cost J at each iterationif i<100000:      # prevent resource exhaustion J_history.append( cost_function(X, y, w, b))# Print cost every at intervals 10 times or as many iterations if < 10if i% math.ceil(num_iters / 10) == 0:print(f"Iteration {i:4d}: Cost {J_history[-1]:8.2f}   ")return w, b, J_history #return final w,b and J history for graphing

测试一下

# initialize parameters
initial_w = np.zeros_like(w_init)
initial_b = 0.
# some gradient descent settings
iterations = 1000
alpha = 5.0e-7
# run gradient descent 
w_final, b_final, J_hist = gradient_descent(X_train, y_train, initial_w, initial_b, compute_cost, compute_gradient, alpha, iterations)
print(f"b,w found by gradient descent: {b_final:0.2f},{w_final} ")
m,_ = X_train.shape
for i in range(m):print(f"prediction: {np.dot(X_train[i], w_final) + b_final:0.2f}, target value: {y_train[i]}")

绘图可视化损失和迭代步数

# plot cost versus iteration  
fig, (ax1, ax2) = plt.subplots(1, 2, constrained_layout=True, figsize=(12, 4))
ax1.plot(J_hist)
ax2.plot(100 + np.arange(len(J_hist[100:])), J_hist[100:])
ax1.set_title("Cost vs. iteration");  ax2.set_title("Cost vs. iteration (tail)")
ax1.set_ylabel('Cost')             ;  ax2.set_ylabel('Cost') 
ax1.set_xlabel('iteration step')   ;  ax2.set_xlabel('iteration step') 
plt.show()

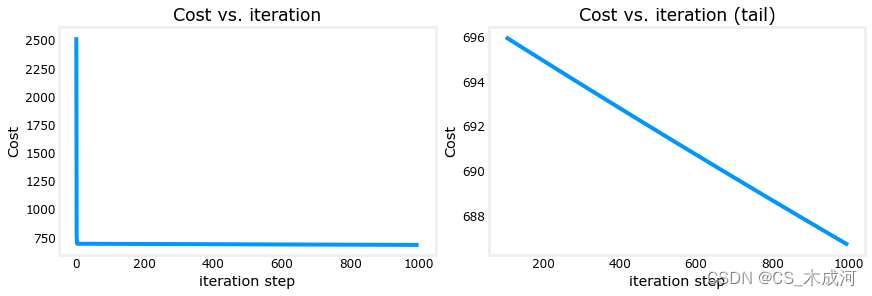
由此可以看出，损失仍在下降，而我们的预测并不是非常准确。下一个博客将探讨如何改进这一点。