子数组的解释与专题
子数组:指在一个数组中,选择一些连续的元素组成的新数组。
例题一:6900. 统计完全子数组的数目
给你一个由 正 整数组成的数组 nums 。
如果数组中的某个子数组满足下述条件,则称之为 完全子数组 :
- 子数组中 不同 元素的数目等于整个数组不同元素的数目。
返回数组中 完全子数组 的数目。
子数组 是数组中的一个连续非空序列。
示例 1:
输入:nums = [1,3,1,2,2] 输出:4 解释:完全子数组有:[1,3,1,2]、[1,3,1,2,2]、[3,1,2] 和 [3,1,2,2] 。示例 2:
输入:nums = [5,5,5,5] 输出:10 解释:数组仅由整数 5 组成,所以任意子数组都满足完全子数组的条件。子数组的总数为 10 。提示:
1 <= nums.length <= 10001 <= nums[i] <= 2000
思路:1.用set以及unerdered_set容器暴力枚举
2.滑动窗口
AC代码:
//暴力
class Solution {
public:int countCompleteSubarrays(vector<int>& nums) {int sum=0;set<int> s;for(auto& x:nums)s.insert(x);int l=nums.size();for(int i=0;i<l;i++){unordered_set<int> ss;for(int j=i;j<l;j++){ss.insert(nums[j]);if(s.size()==ss.size())sum++;}}return sum;}
};//滑动窗口
class Solution {
public:int countCompleteSubarrays(vector<int> &nums) {int m = unordered_set<int>(nums.begin(), nums.end()).size();unordered_map<int, int> cnt;int ans = 0, left = 0;for (int v: nums) { // 枚举子数组右端点 v=nums[i]cnt[v]++;while (cnt.size() == m) {int x = nums[left++];if (--cnt[x] == 0)cnt.erase(x);}ans += left; // 子数组左端点 < left 的都是合法的}return ans;}
};例题二:5057. 截断数组
给定一个长度为 n 的正整数数组a1,a2,…,an 和一个正整数 p。
现在,要将该数组从中间截断,得到两个非空子数组。
我们规定,一个数组的价值等于数组内所有元素之和模 p 的结果。
我们希望,将给定数组截断后,得到的两个非空子数组的价值之和尽可能大。
请你输出这两个非空子数组的价值之和的最大可能值。
输入格式
第一行包含两个整数 n 和 p。
第二行包含 n个整数 a1,a2,…,an。
输出格式
一个整数,表示价值之和的最大可能值。
数据范围
前 33 个测试点满足 2≤n≤10。
所有测试点满足 2≤n≤1e5,2≤p≤10000,1≤ai≤1e6。
输入样例1:
4 10
3 4 7 2
输出样例1:
16
输入样例2:
10 12
16 3 24 13 9 8 7 5 12 12
输出样例2:
13思路:前缀和+枚举
AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5+10;
int a[N],n,p,sum[N],ans;
int sumn;
void solve()
{cin>>n>>p;for(int i=0;i<n;i++){cin>>a[i];sumn += a[i];}sum[0] = a[0];for(int i=1;i<n;i++){sum[i] = sum[i-1]+a[i];}if(n == 2){int cnt = a[0] % p + a[1] % p; cout<<cnt<<endl;return ;}for(int i=1;i<n-1;i++){int tmp = sum[i-1]%p+(sumn-sum[i-1])%p;ans = max(ans,tmp);}cout<<ans<<endl;return ;
}
signed main()
{int t=1;while(t--)solve();return 0;
}今日推荐音乐:落单恋人
下一篇:Codeforces Round 889 (Div. 2)
相关文章:

子数组的解释与专题
子数组:指在一个数组中,选择一些连续的元素组成的新数组。 例题一:6900. 统计完全子数组的数目 给你一个由 正 整数组成的数组 nums 。 如果数组中的某个子数组满足下述条件,则称之为 完全子数组 : 子数组中 不同 …...
PHP: 开发入门macOS系统下的安装和配置
安装Homebrew 安装 ~~友情提示:这个命令对网络有要求,可能需要翻墙或者用你的手机热点试试,或者把DNS换成(114.114.114.114 和 8.8.8.8) /bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebr…...

在CentOS下安装docker
1)在Cent OS安装docker先有一个Cent OS 7.6系统 这个很重要,不同版本按照的时候是不一样的。 2)查看CentOS版本 cat /etc/redhat-releas 3)用root账户登录进去配置国内yum源 wget -O /etc/yum.repos.d/CentOS-Base.repo http:…...

[JavaWeb]SQL介绍-DQL查询数据
SQL介绍-DQL查询数据 一.基础查询二.条件查询三.排序查询1.聚合函数2.分组查询 四.分页查询 DQL查询基础的语法结构如下: SELECT字段列表 FROM表名列表 WHERE条件列表 GROUP BY分组字段 HAVING分组后条件 ORDER BY排序字段 LIMIT分页限定一.基础查询 说明语法查询…...
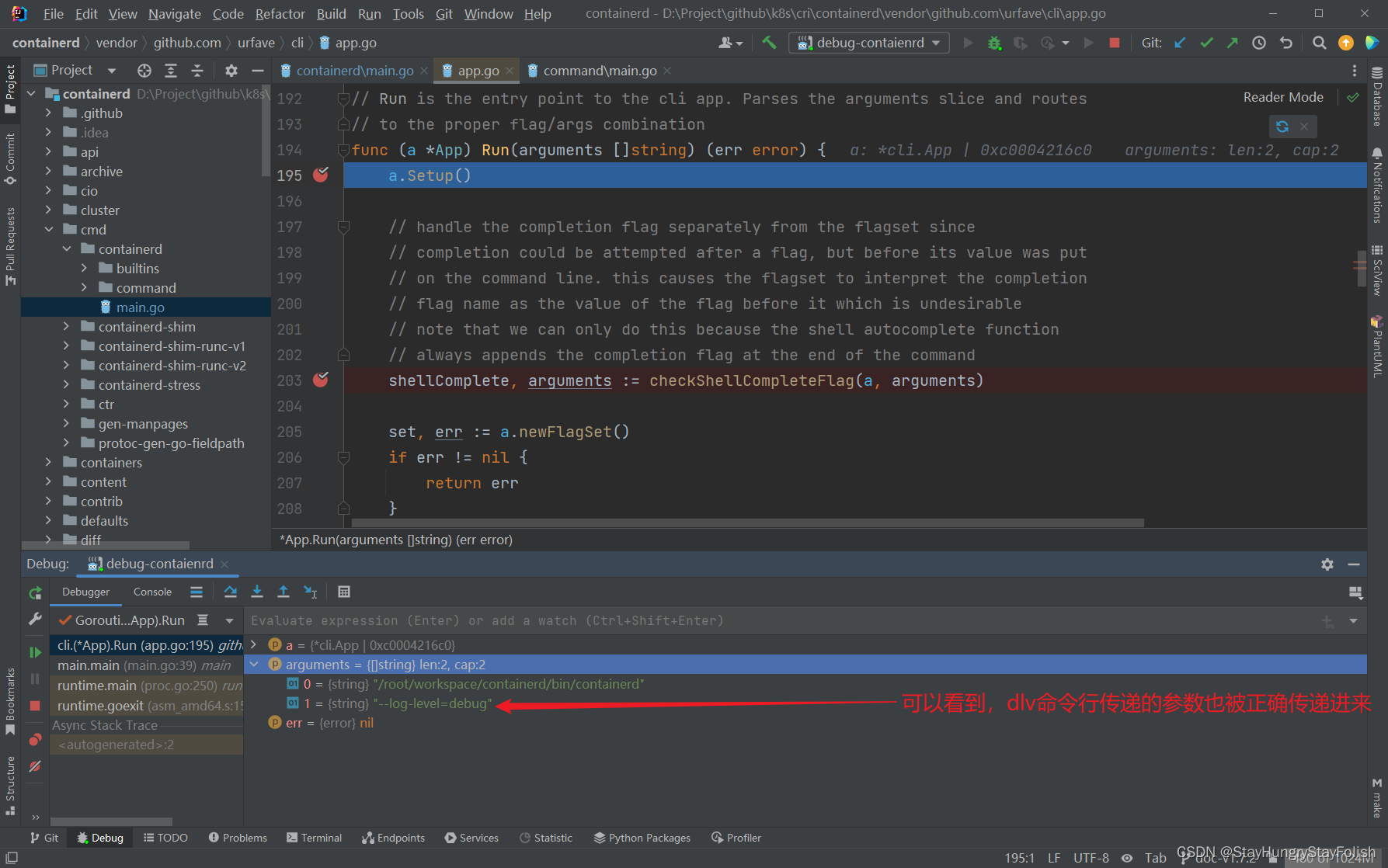
[containerd] 在Windows上使用IDEA远程调试containerd, ctr, containerd-shim
文章目录 1. containerd安装2. 源码编译3. 验证编译的二进制文件是否含有调试需要的信息3.1. objdump工具验证3.2. file工具验证3.3. dlv工具验证 4. debug 1. containerd安装 [Ubuntu 22.04] 安装containerd 2. 源码编译 主要步骤如下: 1、从github下载containe…...

Verilog语法学习——LV4_移位运算与乘法
LV4_移位运算与乘法 题目来源于牛客网 [牛客网在线编程_Verilog篇_Verilog快速入门 (nowcoder.com)](https://www.nowcoder.com/exam/oj?page1&tabVerilog篇&topicId301) 题目 题目描述: 已知d为一个8位数,请在每个时钟周期分别输出该数乘1/…...

打卡力扣题目九
#左耳听风 ARST 打卡活动重启# 目录 一、问题 二、解题方法一 三、解题方法二 四、两种方法的区别 关于 ARTS 的释义 —— 每周完成一个 ARTS: ● Algorithm: 每周至少做一个 LeetCode 的算法题 ● Review: 阅读并点评至少一篇英文技术文章 ● Tips: 学习至少一个…...

Python零基础入门(九)——函数,类和对象
系列文章目录 个人简介:机电专业在读研究生,CSDN内容合伙人,博主个人首页 Python入门专栏:《Python入门》欢迎阅读,一起进步!🌟🌟🌟 码字不易,如果觉得文章不…...
在linux上面部署activemq
1、下载 网址:ActiveMQ 注意:新版本5.17起 要求jdk11, 5.16兼容jdk8, 所以,确保已经安装 java11 或以上的版本 这里安装较新版:5.18.2,已经安装了java17 如何安装jdk17,请详见我的另一篇文章:linux…...

mysql的sql语句优化方法面试题总结
mysql的sql语句优化方法面试题总结 不要写一些没有意义的查询,如需要生成一个空表结构: select col1,col2 into #t from t where 10 这类代码不会返回任何结果集,但是会消耗系统资源的,应改成这样: create table #t…...
小程序 获取用户头像、昵称、手机号的组件封装(最新版)
在父组件引入该组件 <!-- 授权信息 --><auth-mes showModal"{{showModal}}" idautnMes bind:onConfirm"onConfirm"></auth-mes> 子组件详细代码为: authMes.wxml <!-- components/authMes/authMes.wxml --> <van-popup show…...

【Linux】简易shell外壳的制作
#include <stdio.h> #include <unistd.h> #include <string.h> #include <stdlib.h> #include <sys/types.h> #include <sys/wait.h>#define NUM 1024 #define SIZE 32 #define SEP " "// 保存完整的命令行字符串 char cmd_line…...
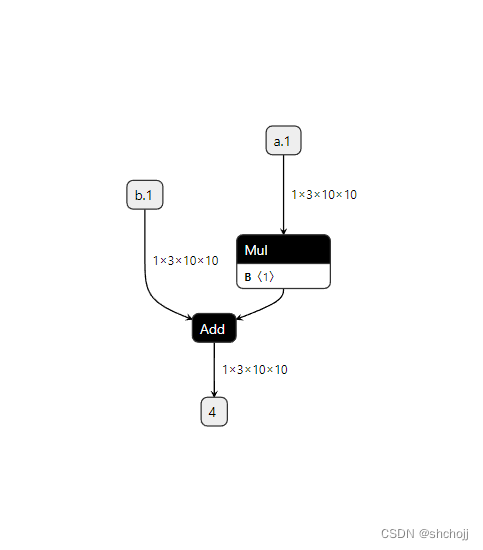
TenserRT(四)在 PYTORCH 中支持更多 ONNX 算子
第四章:在 PyTorch 中支持更多 ONNX 算子 — mmdeploy 0.12.0 文档 PyTorch扩充。 PyTorch转换成ONNX: PyTorch有实现。PyTorch可以转化成一个或者多个ONNX算子。ONNX有相应算子。 如果即没有PyTorch实现,且缺少PyTorch与ONNX的映射关系&…...

前端高级面试题-浏览器
1 事件机制 事件触发三阶段 document 往事件触发处传播,遇到注册的捕获事件会触发 传播到事件触发处时触发注册的事件 从事件触发处往 document 传播,遇到注册的冒泡事件会触发 事件触发⼀般来说会按照上⾯的顺序进⾏,但是也有特例&#x…...
)
Mongodb 多文档聚合操作处理方法三(聚合管道)
聚合 聚合操作处理多个文档并返回计算结果。您可以使用聚合操作来: 将多个文档中的值分组在一起。 对分组数据执行操作以返回单个结果。 分析数据随时间的变化。 要执行聚合操作,您可以使用: 聚合管道 单一目的聚合方法 Map-reduce 函…...
Zabbix分布式监控配置和使用
目录 1 Zabbix监控的配置流程2 添加主机组3 添加模板4 添加主机5 配置图形6 配置大屏7 新建监控项7.1 简介7.2 添加监控项7.3 查看数据7.4 图表 8 新建触发器8.1 概述8.2 添加触发器8.3 显示触发器状态 1 Zabbix监控的配置流程 在Zabbix-Web管理界面中添加一个主机,…...
XCTF_very_easy_sql
简单的进行sql注入测试后发现不简单尝试一下按照提示 结合这句提示应该是内部访问,所以采用的手段应该是ssrf顺便看看包 唯一值得关注的是set-cookie说回ssrf唯一能使用的方式应该是Gopher协议找到了一个POST的python脚本 import urllib.parsepayload ""…...

[React]useMemoizedFn和useCallback对比
useMemoizedFn文档地址:https://ahooks.js.org/zh-CN/hooks/use-memoized-fn hooks组件内什么时候会更新自定义函数 在 React 中,自定义的 Hooks 内部的函数在以下常见的几种情况下会被重新赋值,导致更新引用: 组件重新渲染&…...

计算机毕设 深度学习人体跌倒检测 -yolo 机器视觉 opencv python
文章目录 0 前言1.前言2.实现效果3.相关技术原理3.1卷积神经网络3.1YOLOV5简介3.2 YOLOv5s 模型算法流程和原理4.数据集处理3.1 数据标注简介3.2 数据保存 5.模型训练 6 最后 0 前言 🔥 这两年开始毕业设计和毕业答辩的要求和难度不断提升,传统的毕设题…...

完全背包
动态规划解题步骤 : 动态规划问题一般从三个步骤进行考虑。 步骤一:集合和集合的状态 所谓的集合,就是一些方案的集合。 用 g[i][j] 表示从前 i 种物品中进行选择,且总体积不大于 j 的各个选法获得的价值的集合。注意:g[i][j] 不是一个数…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
