【GD32F427开发板试用】使用Arm-2D显示电池电量
本篇文章来自极术社区与兆易创新组织的GD32F427开发板评测活动,更多开发板试用活动请关注极术社区网站。作者:boc
【虽迟但到】
由于快递的原因,11月份申请的,12月1日才收到GD32F427开发板。虽然姗姗来迟,但也没有减少对他的期待。这不,收到板子后,赶紧焊接插针,连接SPI屏幕,如下图

连接好后,马不停蹄地赶快点亮LCD屏幕,并移植好Arm-2D,显示一个电池电量的小demo,效果演示如下:
https://www.bilibili.com/video/BV1fg411n7wywww.bilibili.com/video/BV1fg411n7wy
怎么样,效果还可以吧。
【Arm-2D简介】
首先,我们简单介绍一下Arm-2D是什么。他是arm公司开源的2d图形加速引擎,由于它支持pfb技术,所以Arm-2D对小资源单片机(flash<64K,ram<32K)的支持也非常好.
当然了,他的移植也非常简单,大家可以看下面这个教程
Arm-2D移植教程
当然,Arm-2D的更多玩法,大家也可以参考这个
【玩转Arm-2D】系列文章
| Arm-2D的开源仓库如下: | |
|---|---|
| https://github.com/ARM-softwa…. |
【实现电池人】
移植好Arm-2D后,我们先把默认的显示关掉,如下图所示
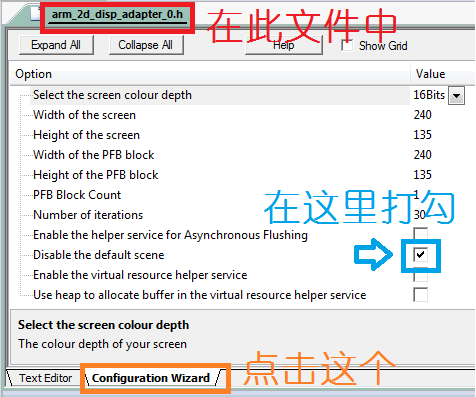
并在main函数中初始化我们自己的scene,如下
arm\_2d\_scene0\_init(&DISP0\_ADAPTER);
这样我们就可以显示自己的界面了,下面我们就开始绘制【电池人】了。
首先,我们找到__pfb_draw_scene0_handler函数,如下图
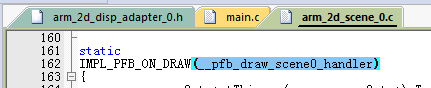
并在此函数中进行绘制,我们在看一下电池小人,如下

,这个炫酷的橘黄色电池控件居然是Arm-2D自带的,他的调用也很简单,如下
`//arm_2d_align_centre( ptTile->tRegion, 100, 130) {
battery_gasgauge_nixie_tube_show( &this.tBatteryNixieTube, ptTile, &__centre_region, this.hwGasgauge,this.tStatus,bIsNewFrame);
//他的原型如下
void battery_gasgauge_nixie_tube_show(
battery_nixie_tube_t *ptThis,
const arm_2d_tile_t *ptTile,
const arm_2d_region_t *ptRegion,
uint16_t hwGasgauge,
battery_status_t tStatus,
bool bIsNewFrame)`
我们简单介绍一下这个battery_gasgauge_nixie_tube_show函数
前两个参数我们不展开讲解了,他主要是Arm-2D自己用的,
- 第3个参数ptRegion,就是电池在屏幕中显示的位置,如下图

- 第4个参数hwGasgauge,就是要显示的电量,他的取值范围为0~999,也就是它除以10就是我们视频中显示的电池电量。
- 第5个参数tStatus,就是指电池是充电状态还是放电状态(它只有两个值:BATTERY_STATUS_CHARGING和BATTERY_STATUS_DISCHARGING)。
- 最后一个参数也是Arm-2D自己用的,我们也不展开讲了,感兴趣大家可以参考上面关于Arm-2D的文章。
好,电池我们就绘制完成了,接下来我们再把电池电量的百分比显示出来,如下:
//显示电量arm_lcd_text_set_draw_region(&__bottom_centre_region);arm_lcd_text_set_colour(GLCD_COLOR_RED, GLCD_COLOR_BLACK);arm_lcd_text_location(0,0);arm_lcd_printf("%02d", this.hwGasgauge / 10);
直接调用arm_lcd_printf就可以了。
那两只眼睛是怎么弄的呢?
它就更简单了,其实就是绘制了两个矩形,如下
myRegion.tSize.iWidth = 14;myRegion.tSize.iHeight = 3;arm_2d_fill_colour(ptTile, &myRegion, GLCD_COLOR_GREEN);myRegion.tLocation.iX += 17;arm_2d_fill_colour(ptTile, &myRegion, GLCD_COLOR_GREEN);
设置一个矩形区域,填充绿色就可以了,简单吧。

不对啊,眼睛明明是一个椭圆,然后变成一个横线啊???
哈哈,其实椭圆也很简单,这个就是用到了Arm-2D提供的圆角矩形函数draw_round_corner_box,如下
//if(time < 7){ myRegion.tLocation.iY -= 2;myRegion.tSize.iWidth = 14;myRegion.tSize.iHeight += 4;//arm_2d_fill_colour(ptTile, &myRegion, GLCD_COLOR_GREEN);draw_round_corner_box(ptTile,&myRegion,GLCD_COLOR_GREEN,150,bIsNewFrame);myRegion.tLocation.iX += 17;//arm_2d_fill_colour(ptTile, &myRegion, GLCD_COLOR_GREEN);draw_round_corner_box(ptTile,&myRegion,GLCD_COLOR_GREEN,150,bIsNewFrame);
然后在定义一个时间变量time,根据不同的时间进行切换就实现了眨眼睛的效果,怎么样,简单吧、。
到这里我们的电池小人就制作完成了。
整个GD32F427的工程文件和Arm-2D移植好的程序我也放到了网盘,供大家参考,如下

最后
衷心祝愿极术社区越办越好,也祝国产单片机GD32也越来越好。
相关文章:

【GD32F427开发板试用】使用Arm-2D显示电池电量
本篇文章来自极术社区与兆易创新组织的GD32F427开发板评测活动,更多开发板试用活动请关注极术社区网站。作者:boc 【虽迟但到】 由于快递的原因,11月份申请的,12月1日才收到GD32F427开发板。虽然姗姗来迟,但也没有减少…...

TS第二天 Typesrcipt编译
文章目录自动编译tsconfig.json配置选项include 比较重要excludeextendsfilescompilerOptions 比较重要自动编译 手动模式:每次ts文件修改完,手动编译一次 tsc 01.ts监视模式:ts文件修改完,自动监视编译 tsc 01.ts -w编译所有文…...
基于C#制作一个飞机大战小游戏
此文主要基于C#制作一个飞机大战游戏,重温经典的同时亦可学习。 实现流程1、创建项目2、界面绘制3、我方飞机4、敌方飞机5、子弹及碰撞检测实现流程 1、创建项目 打开Visual Studio,右侧选择创建新项目。 搜索框输入winform,选择windows窗体…...
git修改历史提交(commit)信息
我们在开发中使用git经常会遇到想要修改之前commit的提交信息,这里记录下怎么使用git修改之前已经提交的信息。一、修改最近一次commit的信息 首先通过git log查看commit信息。 我这里一共有6次commit记录。 最新的commit信息为“Merge branch ‘master’ of https:…...
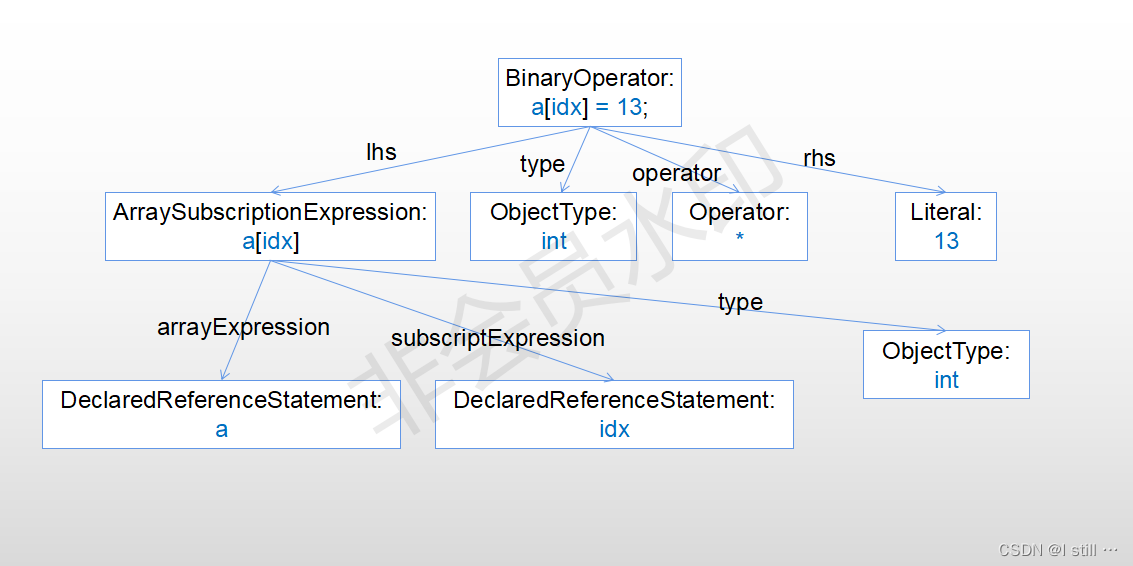
代码解析工具cpg
cpg 是一个跨语言代码属性图解析工具,它目前支持C/C (C17), Java (Java 13)并且对Go, LLVM, python, TypeScript也有支持,在这个项目的根目录下: cpg-core为cpg解析模块的核心功能,主要包括将代码解析为图,core模块只包括对C/C/Ja…...

Linux虚拟机部署Java环境-Jdk-Mysql
Linux虚拟机部署 author hf 1.安装 电脑安装x-shell工具,然后使用堡垒机基础控件windows版进行安装扫描,最后点击自动检测,保证能扫描到X-shell工具的安装路径 使用堡垒机登录快照夏选择工具点击Xshell进行连接 查看linux版本 root:~# ca…...

每日学术速递2.9
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CV、cs.AI、cs.LG、cs.IR 1.Graph Signal Sampling for Inductive One-Bit Matrix Completion: a Closed-form Solution(ICLR 2023) 标题:归纳单比特矩阵完成的图信号采样&am…...

【Linux】进程优先级 | 进程的切换 | 环境变量详解
🤣 爆笑教程 👉 《看表情包学Linux》👈 猛戳订阅 🔥 💭 写在前面:我们先讲解进程的优先级,探讨为什么会存在优先级,以及如何查看系统进程、进程优先级的修改。然后讲解进程的切…...

leaflet 实现左卷帘效果 (代码示例045)
第045个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中实现左卷帘效果,这里主要引用了leaflet-side-by-side这个插件,直接调用的话,CSS方面有些问题,需要自行调整一下。 直接复制下面的 vue+leaflet源代码,操作2分钟即可运行实现效果 文章目录 示例效果配…...

程序的翻译环境和执行环境
程序环境和预处理🦖程序的翻译环境和执行环境🦖详解编译链接🐳 翻译环境🐳 详解编译过程🐳 运行环境🦖预处理详解🐳 预定义符号🐳 #define🦀 #define 定义标识符…...
)
2023最新量化优选股票参考(2.9)
还是周一发的那些股票(可以看我周一的文章),安心持仓就好,跑赢指数是大概率的事情,也大概率获得正收益。 其实我知道大家都没法全天一直看盘操作,毕竟要工作,我也是一样,没法一直看盘…...

深眸科技以科技赋能智慧物流搭建,实现周转箱拆垛作业智能化
数字化时代下市场竞争的核心要素转化为科技的竞争,智能化技术的投入是企业占据市场竞争绝对优势的重要支撑。深眸科技凭借轻辙视觉引擎实现周转箱拆垛作业的智能化突破。人力成本增加,企业积极转变特别是在后疫情时代,人力成本迅猛增加&#…...

R数据分析:孟德尔随机化中介的原理和实操二
delta方法 上面的流程跑通之后,对于中介分析,我们需要报告间接效应的估计值和置信区间,还有中介比例的估计值和置信区间,类似下面的这样: 但是其实我们是光跑孟德尔是得不到上面的需要的值的(比如间接效应…...
:三问(如何对字符串字母去重后按字母顺序排列字符串?如何识别哪些字符串中包含数字?如何将分隔数据转换为多值IN列表?))
【SQL开发实战技巧】系列(十二):三问(如何对字符串字母去重后按字母顺序排列字符串?如何识别哪些字符串中包含数字?如何将分隔数据转换为多值IN列表?)
系列文章目录 【SQL开发实战技巧】系列(一):关于SQL不得不说的那些事 【SQL开发实战技巧】系列(二):简单单表查询 【SQL开发实战技巧】系列(三):SQL排序的那些事 【SQL开发实战技巧…...

数据库模式(schema)是什么?
在数据库的术语中,模式(schema)是一个逻辑概念,用于组织数据库中的对象。模式中的对象通常包括表、索引、数据类型、序列、视图、存储过程、主键、外键等等。 模式可以为数据库对象提供逻辑隔离功能,不用应用程序可以…...
出现failed to load steamui.dll如何解决?好的修复方法推荐
当你电脑突然出现failed to load steamui.dll的时候,你是否一脸懵逼?根本不知道发生啥时候,突然就会这样报错,其实造成这个原因,主要是因为问题出在steam上,我们还是有很多种方法可以解决的,今天…...

js 原生事件触发
var event nullevent new Event(input);document.querySelectorAll("input[placeholder点击网址 选择远端数据字典网址]")[0].dispatchEvent(event)...

Nacos安装配置(二)
目录 一、概述 二、Nacos 安装 A)Debian11 1)软件环境 2)下载源码或者安装包 3)mysql配置 4)启动服务器 B) Debian11 1) 安装JDK 2) 安装Maven 3) 安装Nacos2 4) 修改访问参数(/conf/applicati…...
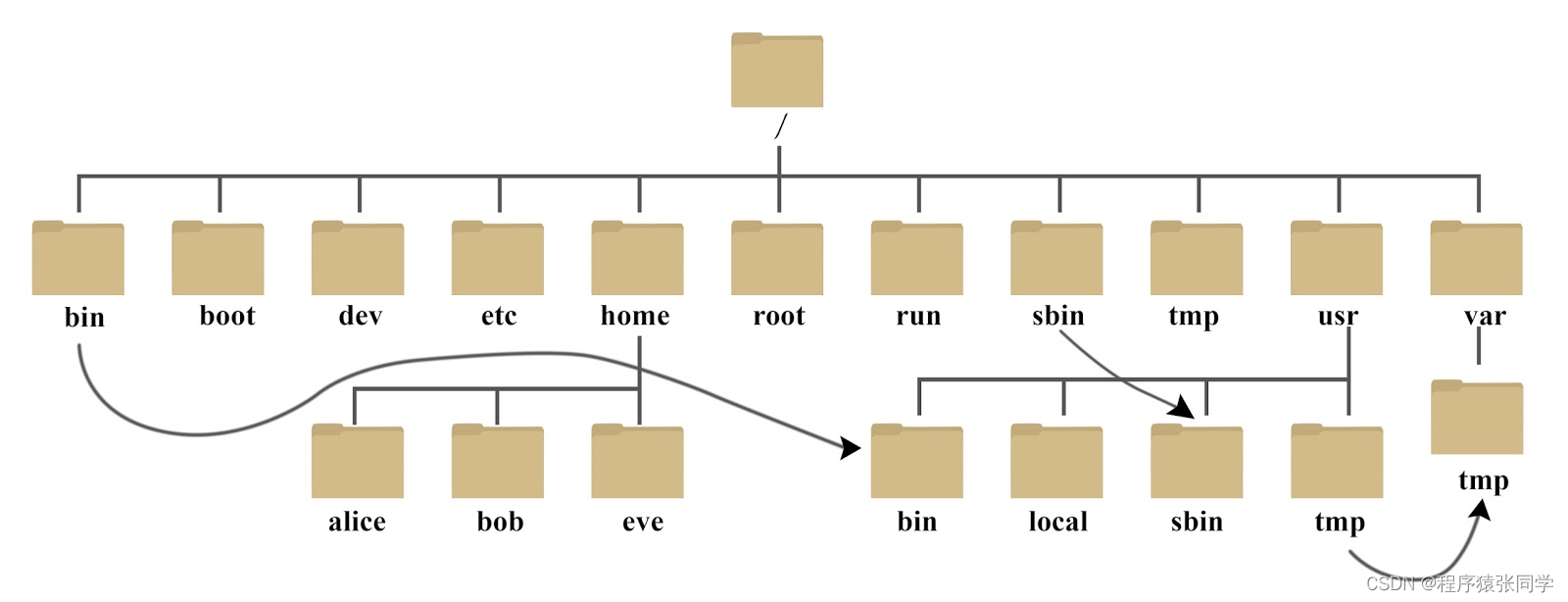
【Linux基础知识】
Linux基础知识 Linux基础知识 系统目录结构 /bin: 命令和应用程序。 /boot: 这里存放的是启动 Linux 时使用的一些核心文件,包括一些连接文件以及镜像文件。 /dev : dev 是 Device(设备) 的缩写, 该目录下存放的是 Linux 的外…...

【王道数据结构】第七章| 查找 | 树
目录 一、查找 1、查找概念 2、顺序查找 3、折半查找 4、分块查找 二、树 1、B树 2、B树的基本操作 3、B树 4、散列查找及其性能分析 5、散列查找及性能分析 一、查找 1、查找概念 查找:在数据集合中寻找满足某种条件的数据元素的过程称为查找。查找…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
