golang 字符串操作、处理
一、golang的字符串长度
1. len()内置系统函数,计算字符串结果是字符串的字节长度,不是字符长度
//1.ASCII字符串长度(字节长度)
str1 := "wo ai zhong guo"
fmt.Println(len(str1)) //15//2.带中文的字符串长度(字节长度)
str2 := "我爱中国"
fmt.Println(len(str2)) //12 4 * 3字节 = 12字节2. 计算带中文的字符串长度。 需要将字符串转为 rune类型(int32)
//带中文的字符串长度str1 := "wo ai 中国"r := []rune(str1)fmt.Println(len(r)) //8//也可以使用 utf8.RuneCountInString() 计算携带中文的字符串长度num := utf8.RuneCountInString(str1)fmt.Println(num) //83.为什么字符串带中文,字符长度计算方式不一样?
因为golang默认的字符编码是utf-8, 字符串的底层是 []byte类型,英文及标点符号都是每个占1个字节,中文占3个字节。 len() 函数实际上计算的是 字符串的字节长度。要计算中文长度,那么就得转成rune 或者 通过 utf8.RuneCountInString(str) 来计算。
二、字符串分割成切片,切片拼接成字符串
//字符串分割str1 := "刘备,关羽,张飞"s := strings.Split(str1, ",")fmt.Println(s) //切片 [刘备 关羽 张飞]//切片拼接成字符串str2 := strings.Join(s, "-")fmt.Println(str2) //字符串 刘备-关羽-张飞三、字符串查找(字符串中是否存在某些子串)
//1.字符串中是否存在某些字符str := "http://baidu.com/index/index.html"b := strings.Contains(str, "http://") //字符串中是否存在 http头fmt.Println(b) //true//2.某个子串 在字符串中有多少个count := strings.Count(str, "index")fmt.Println(count) //2//3.字串在字符串中开始索引位置index := strings.Index(str, "bai")fmt.Println(index) //7//4.字串在字符串中最后一次索引位置index = strings.LastIndex(str, "index")fmt.Println(index) //23四、剔除字符串左右空格及左右指定字符
//1.字符串去左右空格str1 := " 野蛮生长 "fmt.Println(utf8.RuneCountInString(str1)) //字符长度6str := strings.TrimSpace(str1)fmt.Println(str)fmt.Println(utf8.RuneCountInString(str)) //字符长度4 去掉了左右空格//2.去掉左右指定字符str2 := "-野蛮生长-"str = strings.Trim(str2, "-")fmt.Println(str) //野蛮生长//3.去掉左侧指定字符str3 := "-野蛮生长-"str = strings.TrimLeft(str3, "-")fmt.Println(str) //野蛮生长-//4.去掉右侧指定字符str4 := "-野蛮生长-"str = strings.TrimRight(str4, "-")fmt.Println(str) //-野蛮生长五、字符串中的某些字符替换
//1.字符串中某个字符替换掉str := "123 + 456 + 789 = ?"str1 := strings.Replace(str, "+", "-", 1) //替换掉一个fmt.Println(str1) //123 - 456 + 789 = ?str2 := strings.Replace(str, "+", "-", 2) //替换掉两个fmt.Println(str2) //123 - 456 - 789 = ?str3 := strings.ReplaceAll(str, "+", "-") //替换掉所有fmt.Println(str3) //123 - 456 - 789 = ?六、数字字符串转数字(int),int转数字字符串
//1.数字字符串转intstr1 := "123789ab"number1, _ := strconv.Atoi(str1)fmt.Println(number1) //0str2 := "123789"number2, _ := strconv.Atoi(str2)fmt.Println(number2) //123789//2.int转字符串number := 123456str := strconv.Itoa(number)fmt.Println(str) //123789fmt.Println(reflect.TypeOf(str)) //string相关文章:

golang 字符串操作、处理
一、golang的字符串长度 1. len()内置系统函数,计算字符串结果是字符串的字节长度,不是字符长度 //1.ASCII字符串长度(字节长度) str1 : "wo ai zhong guo" fmt.Println(len(str1)) //15//2.带中文的字符串长度&…...
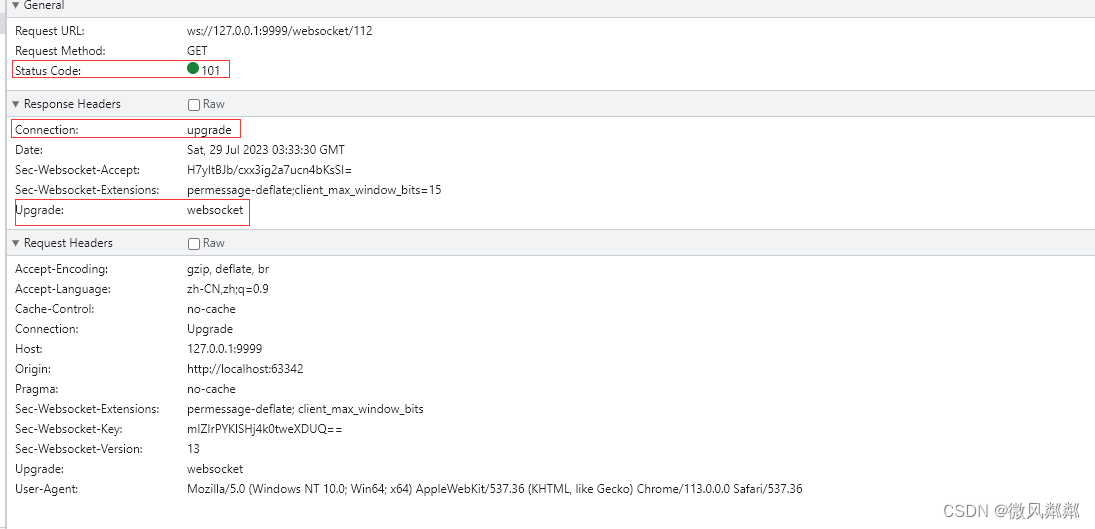
Nginx配置WebSocket反向代理
1、WebSocket协议 WebSocket协议相比较于HTTP协议成功握手后可以多次进行通讯,直到连接被关闭。但是WebSocket中的握手和HTTP中的握手兼容,它使用HTTP中的Upgrade协议头将连接从HTTP升级到WebSocket。这使得WebSocket程序可以更容易的使用现已存在的…...

devops(后端)
1.前言 该devpos架构为gitlabjenkinsharbork8s,项目是java项目,流程为从gitlab拉取项目代码到jenkins,jenkins通过maven将项目代码打成jar包,通过dockerfile构建jdk环境的镜像并把jar包放到镜像中启动,构建好的镜像通…...

Ubuntu安装企业微信
Ubuntu安装企业微信_ubuntu下安装企业微信_星光2020的博客-CSDN博客 在Ubuntu环境安装企业微信可以参考 https://github.com/zq1997/deepin-wine 所述的方法 首先运行 $ wget -O- https://deepin-wine.i-m.dev/setup.sh | sh 然后就可以像安装其它软件一样安装企业微信或其它…...
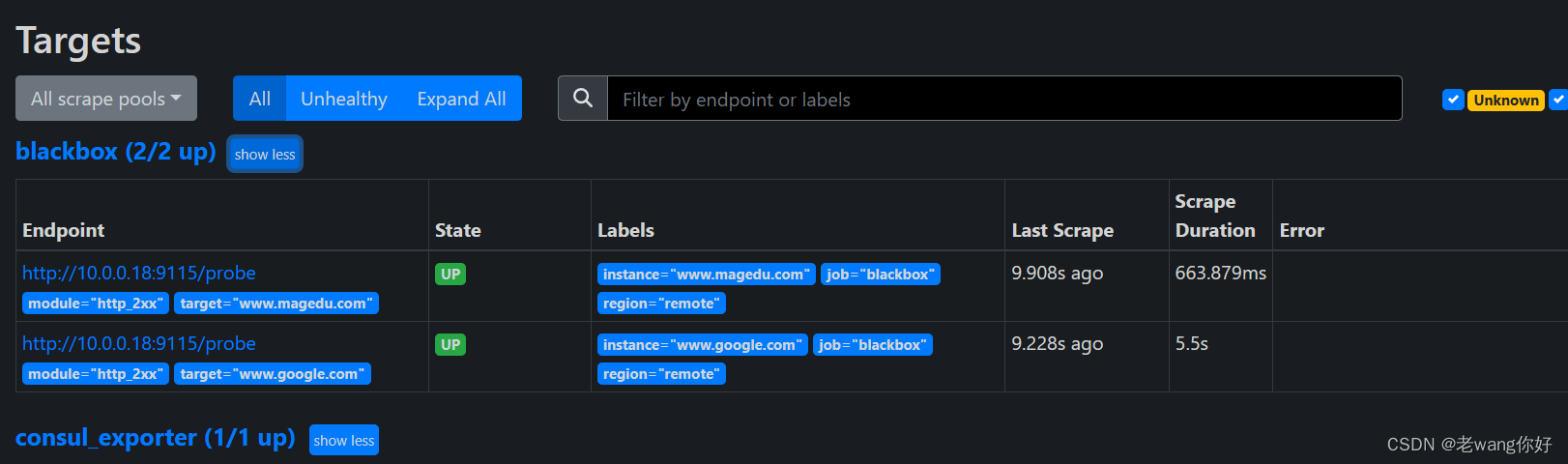
Prometheus 的应用服务发现及黑河部署等
目录 promtool检查语法 部署Prometheus Server 检查语法是否规范 部署node-exporter 部署Consul 直接请求API进行服务注册 使用register命令注册服务(建议使用) 单个和多个注册,多个后面多加了s 在Prometheus上做consul的服务发现 部署…...

JAVA SE -- 第十二天
(全部来自“韩顺平教育”) 常用类 一、包装类 1、包装类的分类 ①针对八种基本数据类型相应的引用类型--包装类 ②有了类的特点,就可以调用类中的方法 ③ 基本数据类型包装类booleanBooleancharCharacterbyteByteshortShortintInteger…...
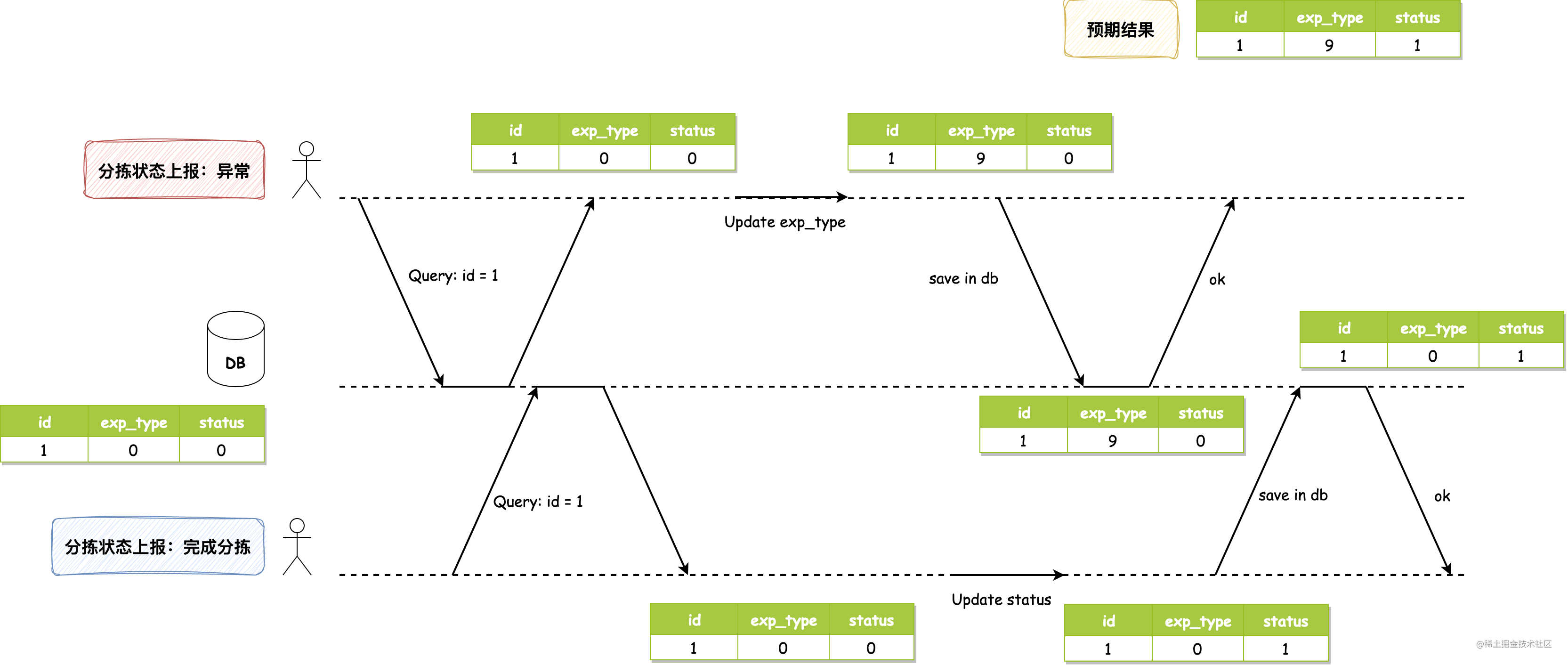
实战:工作中对并发问题的处理
大家好,我是 方圆。最近在接口联调时发生了数据并发修改问题,我想把这个问题讲解一下,并把当时提出的解决方案进行实现,希望它能在大家以后在遇到同样的问题时提供一些借鉴和思考的方向。原文还是收录在我的 Github: enthusiasm 中…...

腾讯云Cloud Studio:基于Claude快速完成Excel工资自动核算
目录 1 什么是Cloud Studio?2 注册与代码管理2.1 账号注册2.2 Git关联 3 实战:Excel工资自动核算3.1 创建项目与配置3.2 “念咒师”Claude GPT3.3 代码编写与运行 1 什么是Cloud Studio? Cloud Studio是腾讯云为开发者提供的一个基于浏览器的…...

Spring Boot OAuth2 快速入门示例
系统要求 Spring Authorization Server 需要JDK1.8及以上版本。 项目搭建 使用在线项目初始化器 https://start.spring.io/ 生成项目[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ljKbMI4H-1690726855433)(images/screenshot_1690602511482.png)…...

MethodInterceptor
目录 1 MethodInterceptor 1.1 HandleSync 1.2 HandleException 1.3 /// This will be called via Reflection MethodInterceptor HandleSync private void HandleSync(IReadOnlyList<MethodFilterAttribute> filterAttributes, IReadOnlyList<ExceptionFilte…...

PID模块化__以stm32直流电机速度为例
文章目录 前言一、相关PID源码.c.h 二、如何使用1.创建变量2.初始化3.运算4.修改pid参数 总结 前言 本篇使用到的基于这个STM32CubeMX 直流电机PID速度控制、HAL库、cubemx、PID、速度控制、增量式 由于上次使用的pid没有模块化,当多出使用pid的时候就会很麻烦 所以…...
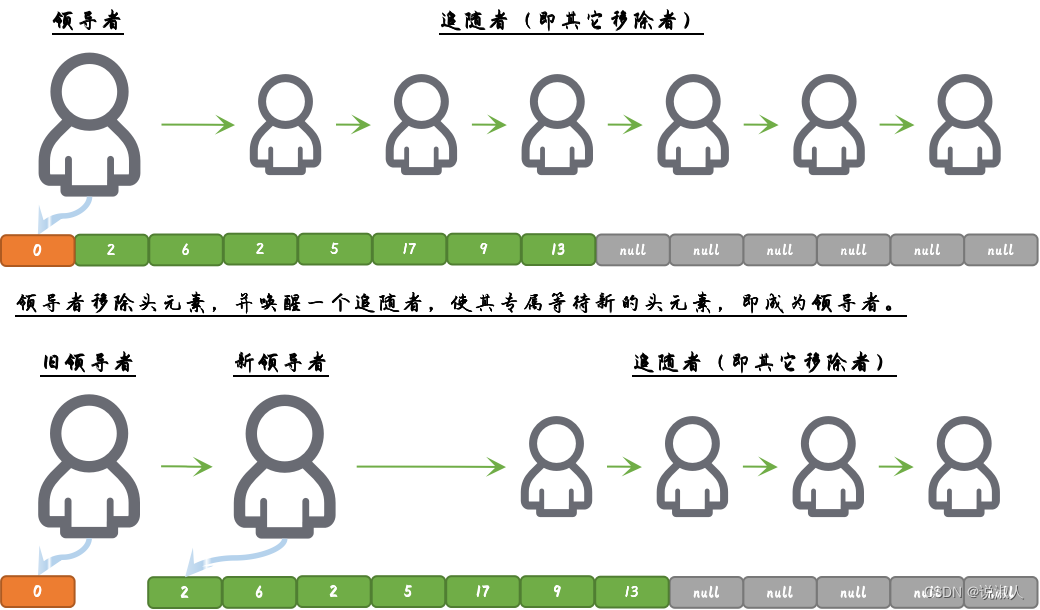
Java ~ Collection/Executor ~ DelayQueue【总结】
前言 文章 相关系列:《Java ~ Collection【目录】》(持续更新)相关系列:《Java ~ Executor【目录】》(持续更新)相关系列:《Java ~ Collection/Executor ~ DelayQueue【源码】》(学…...

前端高级面试题-安全相关
1 XSS 跨⽹站指令码(英语: Cross-site scripting ,通常简称为: XSS )是⼀种⽹站应⽤程式的安全漏洞攻击,是代码注⼊的⼀种。 它允许恶意使⽤者将程式码注⼊到⽹⻚上,其他使⽤者在观看⽹⻚时就会…...
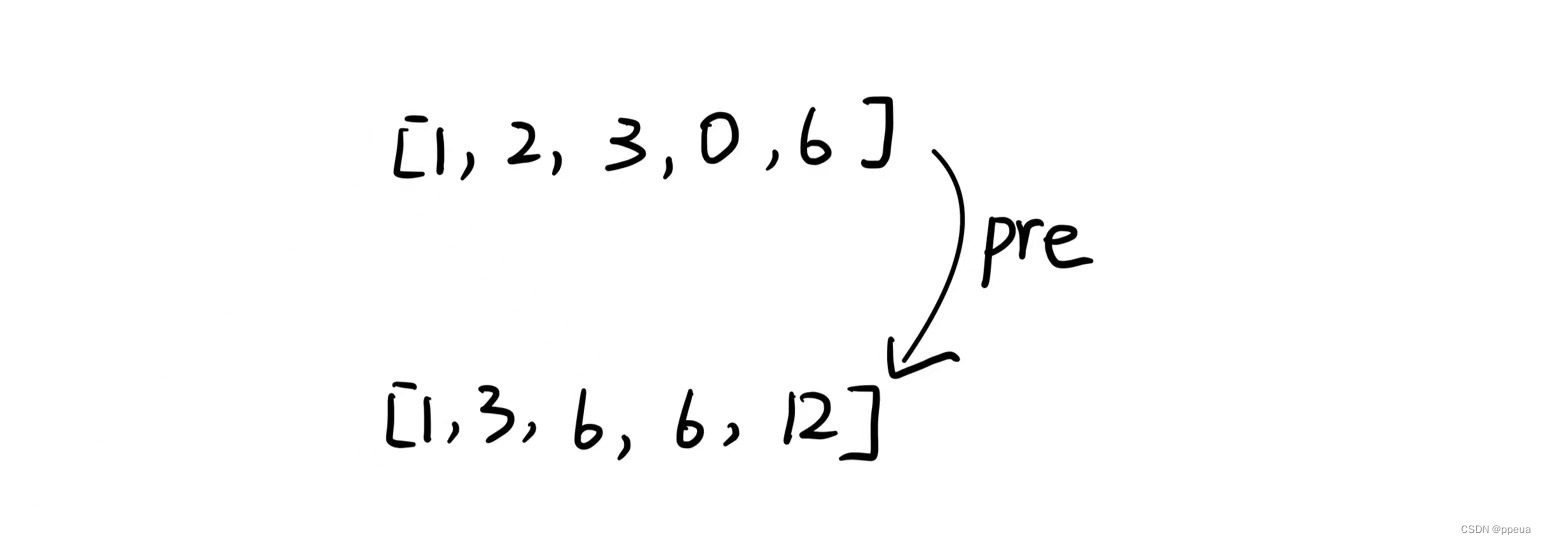
【前缀和】560.和为 K 的子数组
Halo,这里是Ppeua。平时主要更新C,数据结构算法,Linux与ROS…感兴趣就关注我bua! 和为K的子数组 题目:示例:题解:解法一:解法二: 题目: 示例: 题解: 解法一: 暴力解法:我们很容易想到通过两个for循环去遍…...
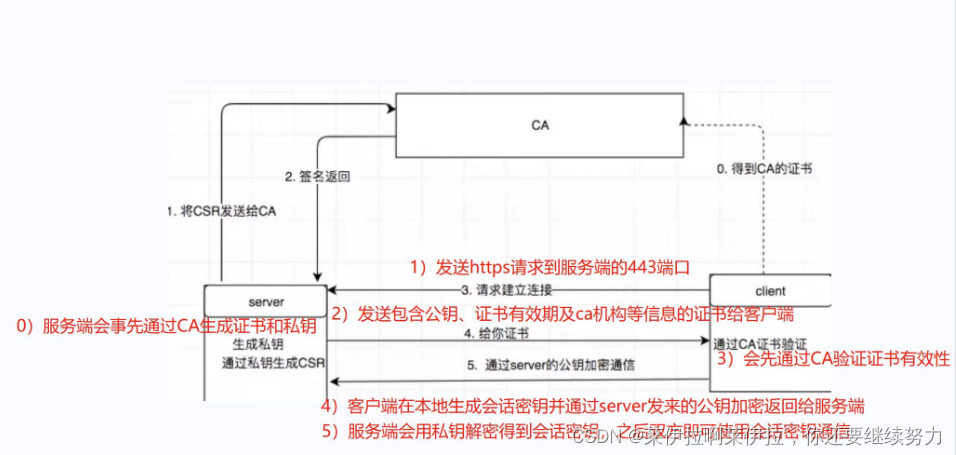
【Docker】安全及日志管理
安全及日志管理 Docker 安全及日志管理一:Docker 容器与虚拟机的区别1. 隔离与共享2. 性能与损耗 二:Docker 存在的安全问题1.Docker 自身漏洞2.Docker 源码问题 三:Docker 架构缺陷与安全机制1. 容器之间的局域网攻击2. DDoS 攻击耗尽资源3.…...
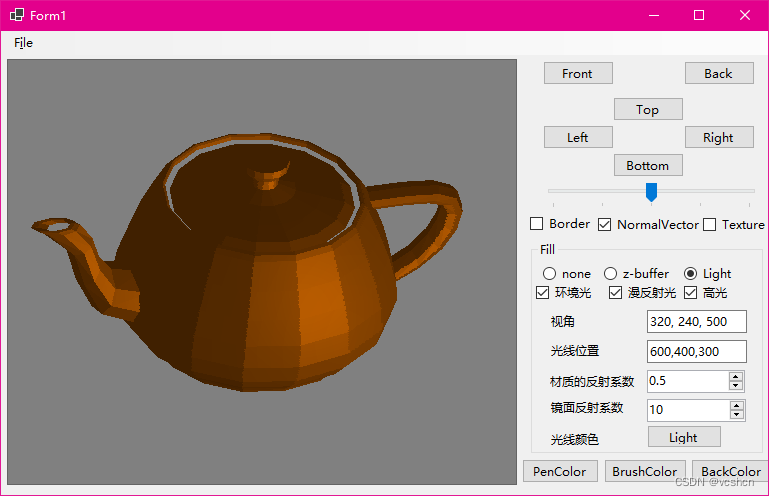
基于x-scan扫描线的3D模型渲染算法
基于x-scan算法实现的z-buffer染色。c#语言,.net core framework 3.1运行。 模型是读取3D Max的obj模型。 x-scan算法实现: public List<Vertex3> xscan() {List<Vertex3> results new List<Vertex3>();SurfaceFormula formula g…...
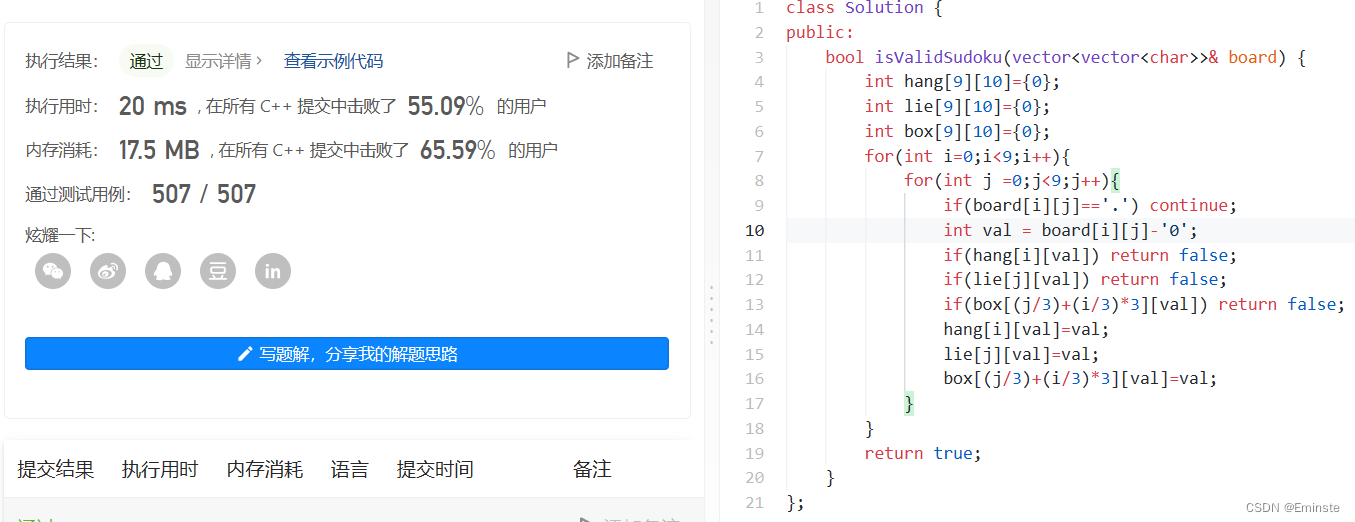
LeetCode36.Valid-Sudoku<有效的数独>
题目: 思路: 这题并不难,它类似于N皇后问题。在N皇后问题中,行,列,对角线,写对角线,都不能出现连续的皇后。 本题类似,不过他是行,列,还有一个B…...
Linux中的pause函数
2023年7月29日,周六上午 函数原型 在Linux中,pause()函数用于使当前进程暂停执行,直到接收到一个信号。 #include <unistd.h>int pause(void);pause()函数不接受任何参数。 通常,pause()函数用于编写简单的信号处理程序&…...

CommonCollections6链分析
前面和CC1一样 优点是不限制jdk版本和cc的版本 先开一个ChainedTransformer 然后创LazyMap 我们顺便执行一下避免上面写错 能弹计算器 没问题 后面就是CC6不同的地方了 我们需要一个TiedMapEntry 因为需要一个类调用了get方法 在TiedMapEntry的getValue()方法中调用了get()…...
优化基于tcp,socket的ftp文件传输程序
原始程序: template_ftp_server_old.py: import socket import json import struct import os import time import pymysql.cursorssoc socket.socket(socket.AF_INET, socket.SOCK_STREAM) HOST 192.168.31.111 PORT 4101 soc.bind((HOST,PORT)) p…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
动态规划-1035.不相交的线-力扣(LeetCode)
一、题目解析 光看题目要求和例图,感觉这题好麻烦,直线不能相交啊,每个数字只属于一条连线啊等等,但我们结合题目所给的信息和例图的内容,这不就是最长公共子序列吗?,我们把最长公共子序列连线起…...
