【前缀和】560.和为 K 的子数组

Halo,这里是Ppeua。平时主要更新C++,数据结构算法,Linux与ROS…感兴趣就关注我bua!
和为K的子数组
- 题目:
- 示例:
- 题解:
- 解法一:
- 解法二:

题目:

示例:

题解:
解法一:
暴力解法:我们很容易想到通过两个for循环去遍历数组中所有和的可能,之后来判断有几个满足K.他的代码十分的简单,所以这里直接给出.
class Solution {
public:int subarraySum(vector<int>& nums, int k) {int count = 0;for (int start = 0; start < nums.size(); ++start) {int sum = 0;for (int end = start; end >= 0; --end) {sum += nums[end];if (sum == k) {count++;}}}return count;}
};
这里通过一个start与end来控制子数组区间.若为K则计数++.
我们仔细观察这样的做法.可以很容易的发现,**我们可以通过前缀和来解决两层循环的问题.**于是就有了解法二:利用前缀和来解决此类问题.
解法二:
不熟悉前缀和的uu们可以看看这篇文章:[前缀和]((138条消息) 【高精度加减乘除法、一维二维前缀和&&差分】思路讲解及代码实现_ppeua的博客-CSDN博客)
这里就直接开始推导了,这里利用的是一维的前缀和方法.
定义:**pre[i]**表示从0~i的所有数组元素之和.
那么根据前缀和的定义:j~i区间内的元素之和可以表示为:pre[i]-pre[j-1],我们要判断的就是这个结果能不能等于K.
所以现在的求解就简化为下面这个式子:
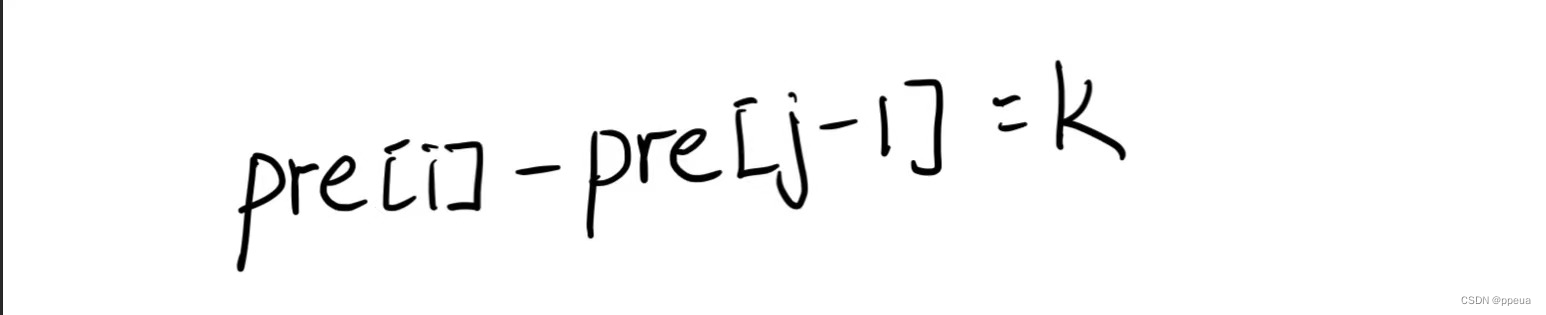
我们对两边式子进行简单的数学推导可以得到.
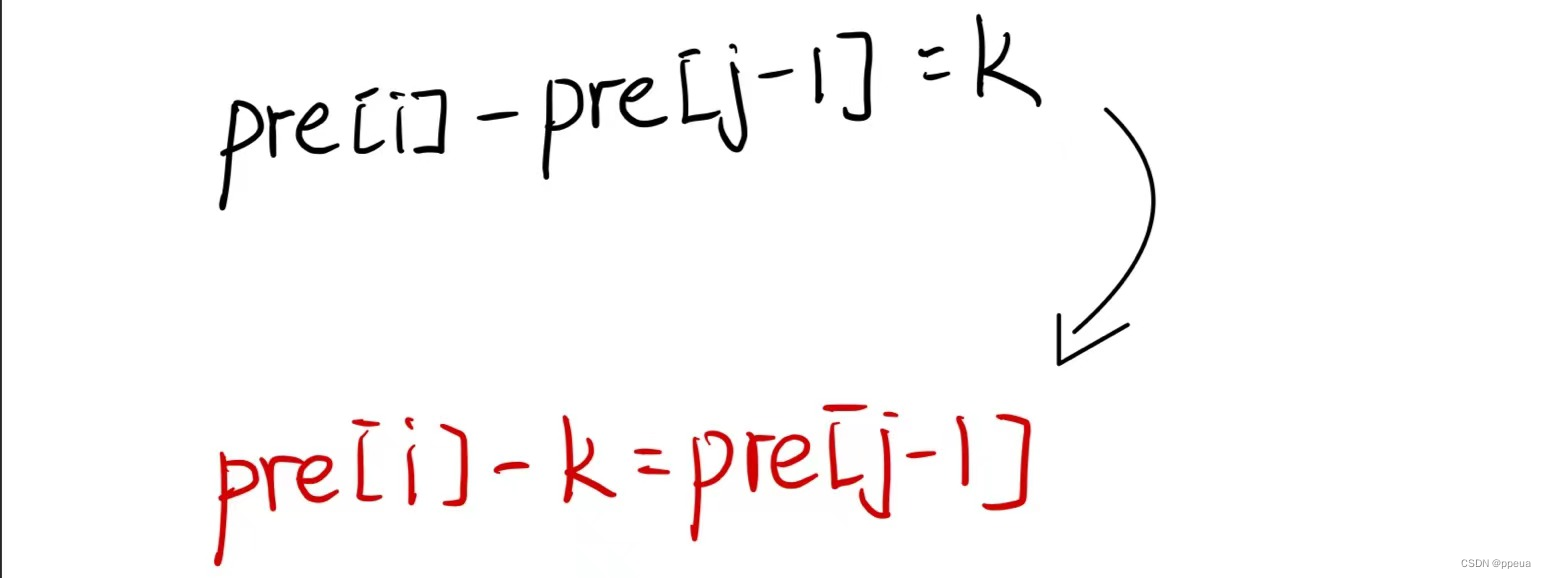
这样我们可以通过一个hash来存储值,之后只要验证当前遍历的这个前缀和-k的结果是否出现在hash当中.若出现则+上其出现的次数.
代码较为简单:
class Solution {
public:int subarraySum(vector<int>& nums, int k) {for(int i=1;i<nums.size();i++){nums[i]+=nums[i-1];}unordered_map<int,int>mp;mp[0]=1;int res=0;for(int i=0;i<nums.size();i++){if(mp.find(nums[i]-k)!=mp.end()){res+=mp[nums[i]-k];}mp[nums[i]]++;}return res;}
};
有两个很重点的问题:
-
为什么mp[0]=1?
为了应对 nums[0] +nums[1] + … + nums[i] == k,也就是从下标 0 累加到下标 i刚好满足的情况.
举个例子:k为6
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-d76gHMzW-1690721194136)(9feab2bfaa7a4eeaaf2882827c8466d.jpg)]](https://img-blog.csdnimg.cn/981f5e0f58844b1a94565b62cd660aaa.png)
当这种情况下,第一次遍历到原数组为3,前缀和数组为6的位置的时候.此时pre-k=0,是刚好满足情况的.所以需要先预设一个mp[0]=1的情况.
-
为什么是res+=mp[nums[i]-k]:
举个例子:K仍为6
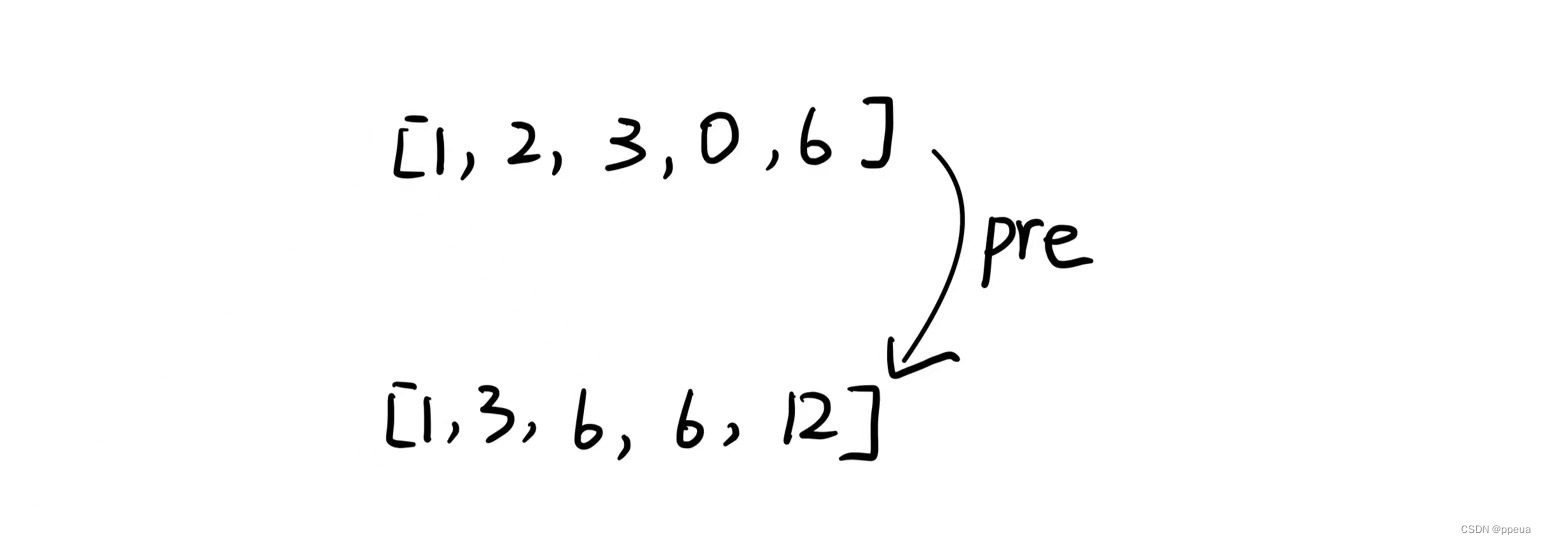
这道题的答案是4,当遍历到第一个6的位置上时,得到第一个答案.遍历到第二个位置时,得到第二个答案.这两种情况都是:pre-k=0
遍历到12时得到第三个答案,此时pre-k=6.那么此时只有三个答案嘛?不是的,12-第一个6是一个答案.12-第二个6也是一个答案.
遍历到第二个位置时,得到第二个答案.这两种情况都是:pre-k=0
遍历到12时得到第三个答案,此时pre-k=6.那么此时只有三个答案嘛?不是的,12-第一个6是一个答案.12-第二个6也是一个答案.
所以:res+=mp[nums[i]-k],是为了直接加上相同情况的可能.
相关文章:
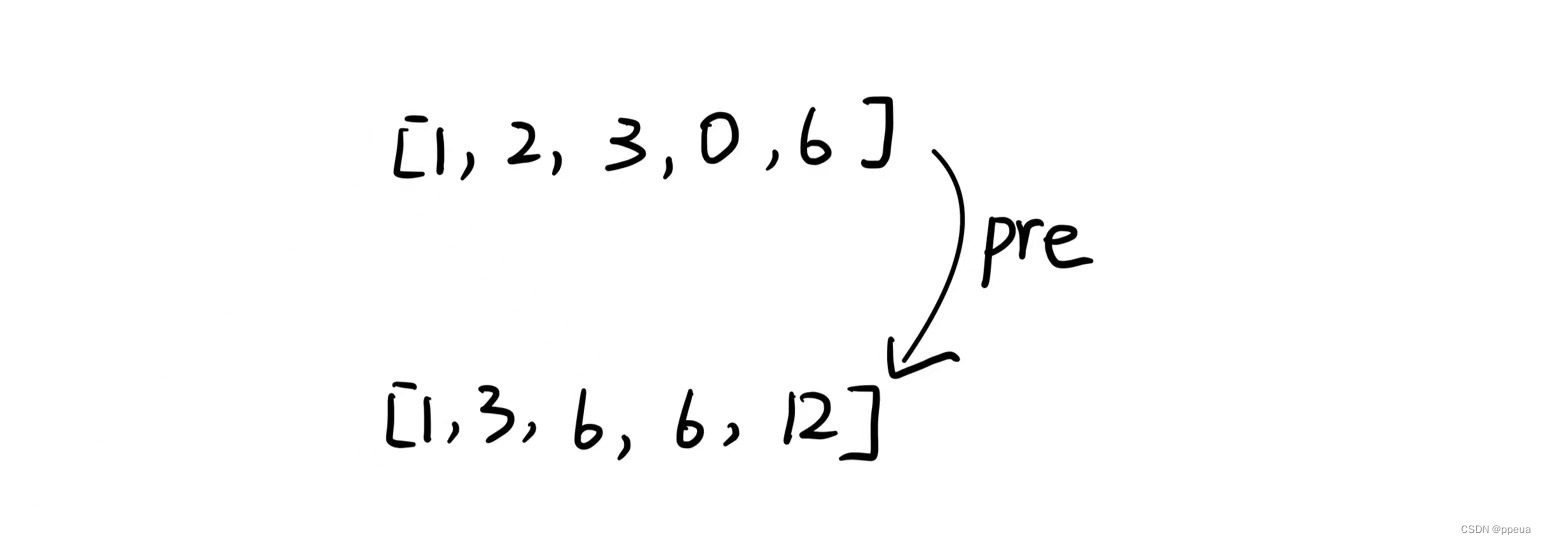
【前缀和】560.和为 K 的子数组
Halo,这里是Ppeua。平时主要更新C,数据结构算法,Linux与ROS…感兴趣就关注我bua! 和为K的子数组 题目:示例:题解:解法一:解法二: 题目: 示例: 题解: 解法一: 暴力解法:我们很容易想到通过两个for循环去遍…...
【Docker】安全及日志管理
安全及日志管理 Docker 安全及日志管理一:Docker 容器与虚拟机的区别1. 隔离与共享2. 性能与损耗 二:Docker 存在的安全问题1.Docker 自身漏洞2.Docker 源码问题 三:Docker 架构缺陷与安全机制1. 容器之间的局域网攻击2. DDoS 攻击耗尽资源3.…...
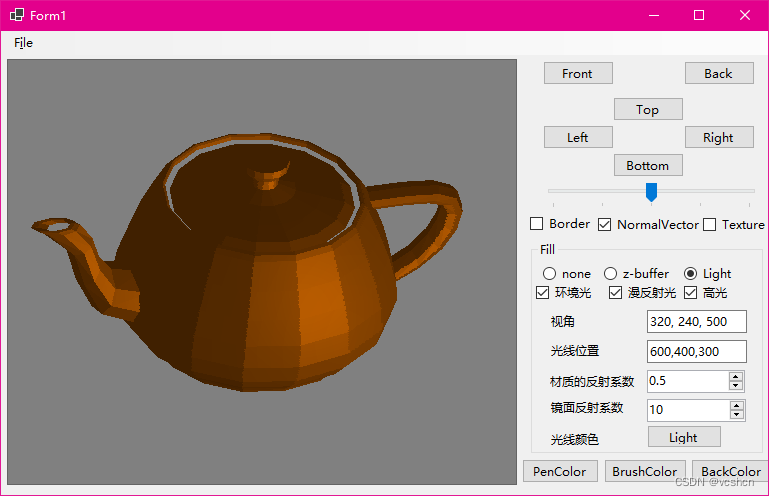
基于x-scan扫描线的3D模型渲染算法
基于x-scan算法实现的z-buffer染色。c#语言,.net core framework 3.1运行。 模型是读取3D Max的obj模型。 x-scan算法实现: public List<Vertex3> xscan() {List<Vertex3> results new List<Vertex3>();SurfaceFormula formula g…...
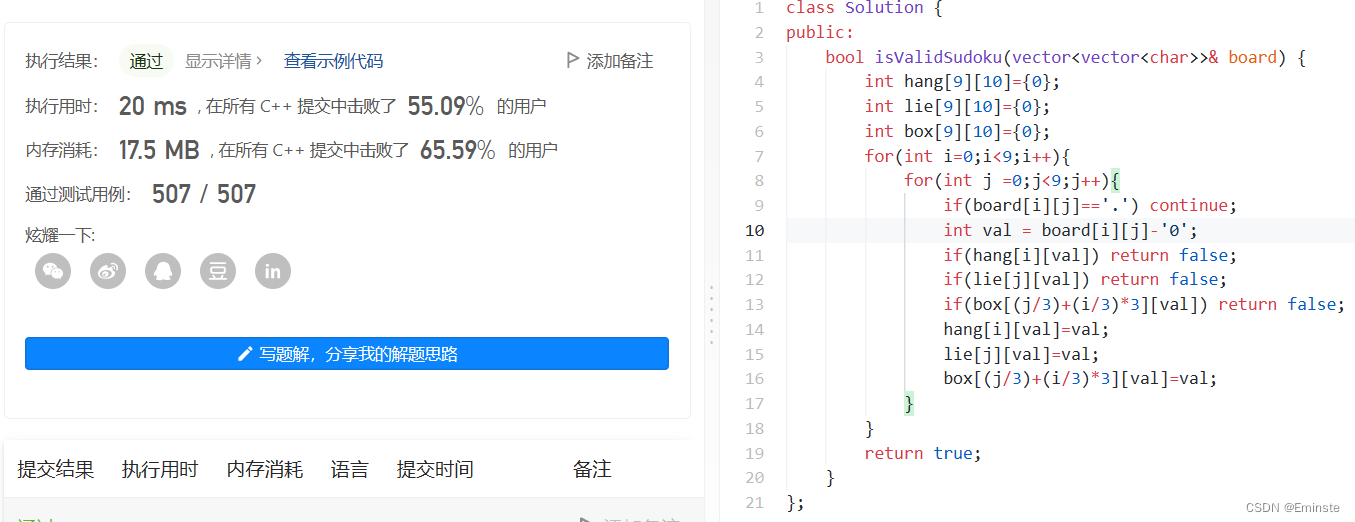
LeetCode36.Valid-Sudoku<有效的数独>
题目: 思路: 这题并不难,它类似于N皇后问题。在N皇后问题中,行,列,对角线,写对角线,都不能出现连续的皇后。 本题类似,不过他是行,列,还有一个B…...
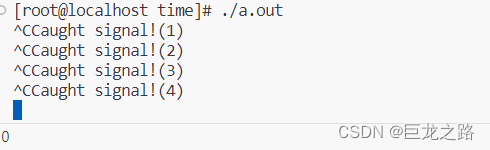
Linux中的pause函数
2023年7月29日,周六上午 函数原型 在Linux中,pause()函数用于使当前进程暂停执行,直到接收到一个信号。 #include <unistd.h>int pause(void);pause()函数不接受任何参数。 通常,pause()函数用于编写简单的信号处理程序&…...

CommonCollections6链分析
前面和CC1一样 优点是不限制jdk版本和cc的版本 先开一个ChainedTransformer 然后创LazyMap 我们顺便执行一下避免上面写错 能弹计算器 没问题 后面就是CC6不同的地方了 我们需要一个TiedMapEntry 因为需要一个类调用了get方法 在TiedMapEntry的getValue()方法中调用了get()…...
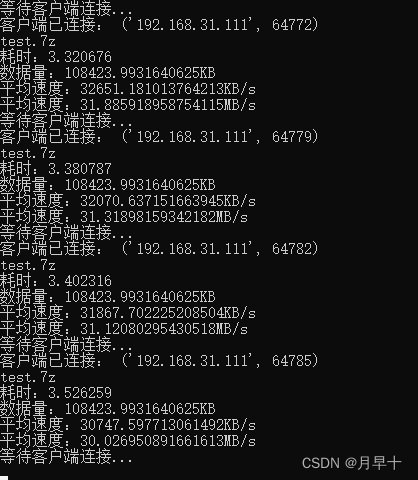
优化基于tcp,socket的ftp文件传输程序
原始程序: template_ftp_server_old.py: import socket import json import struct import os import time import pymysql.cursorssoc socket.socket(socket.AF_INET, socket.SOCK_STREAM) HOST 192.168.31.111 PORT 4101 soc.bind((HOST,PORT)) p…...

MySQL 数据库 【增删查改(二)】
目录 一、表的设计 1、一对一 2、一对多 3、多对多 二、新增 三、查询 1、聚合查询 (1)聚合函数: (2) group by 子句 (3)having 2、联合查询 (1)内连接 (2)外连接 (3)自链接 (4)…...

力扣 -- 978. 最长湍流子数组
一、题目 二、解题步骤 下面是用动态规划的思想解决这道题的过程,相信各位小伙伴都能看懂并且掌握这道经典的动规题目滴。 三、参考代码 class Solution { public:int maxTurbulenceSize(vector<int>& nums) {int nnums.size();vector<int> f(n);…...
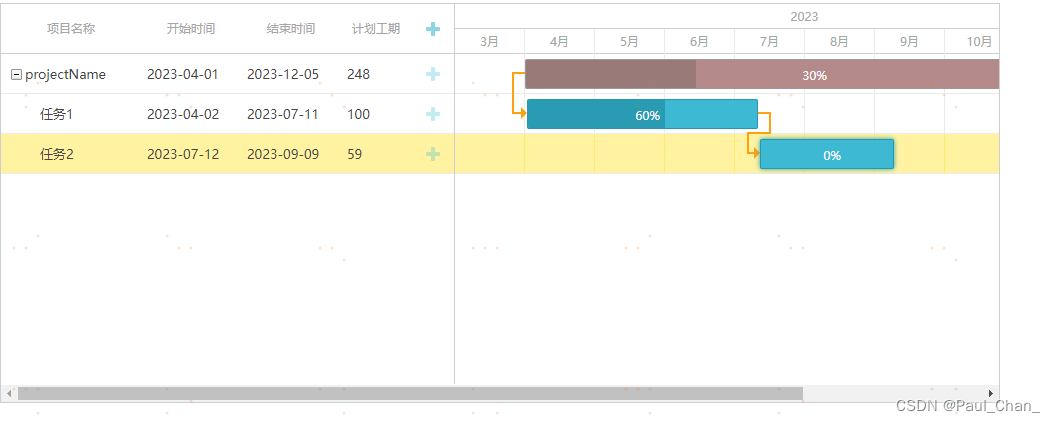
甘特图 Dhtmlx Gantt
介绍 在一些任务计划、日程进度等场景中我们会使用到甘特图,Dhtmlx Gantt 对于甘特图的实现支持很友好,文档API介绍全面,虽然增强版的收费,但免费版的足以够用。 官网:https://docs.dhtmlx.com/gantt/ 安装dhtml gannt…...

iOS 应用上架流程详解
iOS 应用上架流程详解 欢迎来到我的博客,今天我将为大家分享 iOS 应用上架的详细流程。在这个数字化时代,移动应用已经成为了人们生活中不可或缺的一部分,而 iOS 平台的 App Store 则是开发者们发布应用的主要渠道之一。因此,了解…...
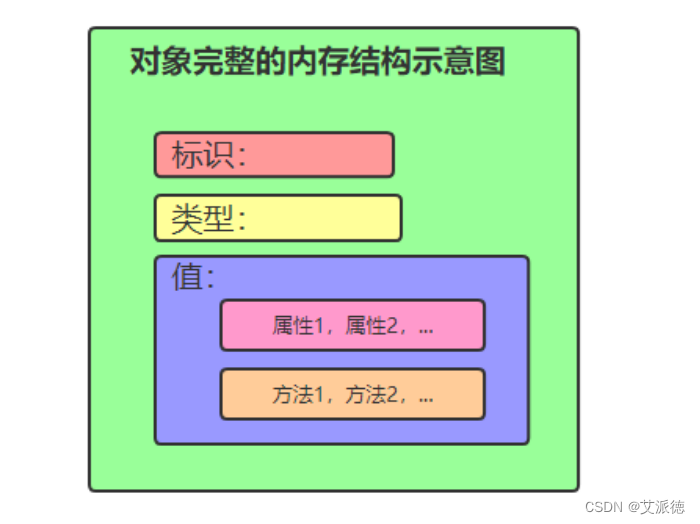
Python入门【LEGB规则、面向对象简介、面向过程和面向对象思想、面向对象是什么? 对象的进化 、类的定义、对象完整内存结构 】(十三)
👏作者简介:大家好,我是爱敲代码的小王,CSDN博客博主,Python小白 📕系列专栏:python入门到实战、Python爬虫开发、Python办公自动化、Python数据分析、Python前后端开发 📧如果文章知识点有错误…...

【消息中间件】原生PHP对接Uni H5、APP、微信小程序实时通讯消息服务
文章目录 视频演示效果前言一、分析二、全局注入MQTT连接1.引入库2.写入全局连接代码 二、PHP环境建立总结 视频演示效果 【uniapp】实现买定离手小游戏 前言 Mqtt不同环境问题太多,新手可以看下 《【MQTT】Esp32数据上传采集:最新mqtt插件(支…...
【C语言初阶】指针篇—上
目录 1. 指针是什么?2. 指针和指针类型2.1 指针-整数2.2 指针的解引用 3. 野指针3.1 野指针成因1. 指针未初始化2. 指针越界访问3. 指针指向的空间释放 3.2 如何规避野指针 1. 指针是什么? 指针是什么? 指针理解的2个要点: > 1…...

基于FasterRCNN深度学习网络的车辆检测算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 MATLAB2022A 3.部分核心程序 ....................................................................... % 训练Faster R-…...
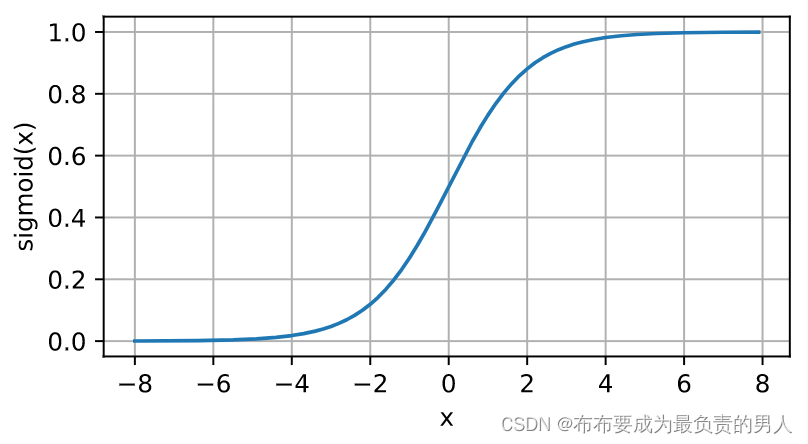
机器学习深度学习——多层感知机
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——感知机 📚订阅专栏:机器学习&&深度学习 希望文章对你们有所帮助 上一节…...

Django模型将模型注释同步到数据库
1、安装django-comment-migrate库 pip install django-comment-migrate 2、将库注册到settings.py文件中 INSTALLED_APPS [...django_comment_migrate, # 表注释... ] 3、加注释 3.1、给模型(表)加注释 在模型的class Meta中编辑 verbose_name&…...
)
STM32 Flash学习(二)
STM32F1的官方固件库操作FLASH的几个常用函数。这些函数和定义分布在源文件stm32f1xx_hal_flash.c/stm32f1xx_hal_flash_ex.c以及头文件stm32f1xx_hal_flash.h/stm32f1xx_hal_flash_ex.h中。 锁定解函数 对FLASH进行写操作前必须先解锁,解锁操作:在FLA…...

kotlin获取泛型集合的类型信息
通过 reified 关键字和内联函数来实现 inline fun <reified T> getClassFromList(list: List<T>): Class<T> {return T::class.java }fun main() {val list listOf("Hello", "World")val clazz getClassFromList(list)println(clazz)…...

AQS源码解析
关于 AQS,网上已经有无数的文章阐述 AQS 的使用及其源码,所以多这么一篇文章也没啥所谓,还能总结一下研究过的源码。源码解析和某某的使用,大概是互联网上 Java 文章中写得最多的主题了。 AQS AQS 是 AbstractQueuedSynchronize…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
