机器学习深度学习——多层感知机
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er
🌌上期文章:机器学习&&深度学习——感知机
📚订阅专栏:机器学习&&深度学习
希望文章对你们有所帮助
上一节已经简单讲解了感知机,并且用XOR函数来举例说明单层感知机的不足,在这里进行多层感知机的讲解。
多层感知机
- 解决XOR
- 隐藏层
- 线性模型可能会出错
- 在网络中加入隐藏层
- 从线性到非线性
- 通用近似定理
- 激活函数
- ReLU函数
- sigmoid函数
- tanh函数
- 多类分类
解决XOR
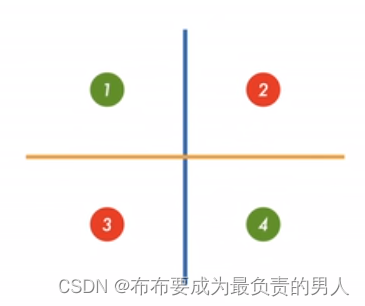
如上图所示,分别利用黄线和蓝线来对输入特征进行分别,并用表格来进行表示:
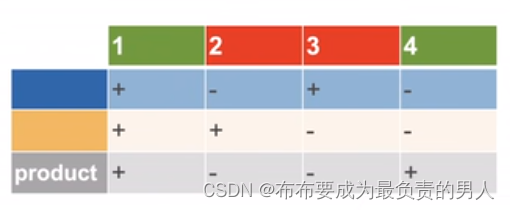
这个表格就直接很容易的体现出了输入和输出的关系,很明显这不是单层感知机能够完成的,而是需要进行如下的过程:
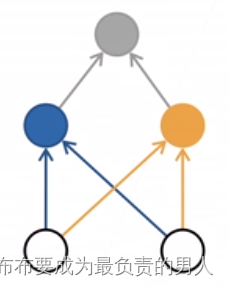
显然,我们要从白圈得到输入的值,从而得知黄圈和蓝圈分别是什么符号再得到灰色的输出值。
简单来讲,这就是一个单隐藏层,也就是说输入和输出之间隐藏了一层运算,单隐藏图如下图:
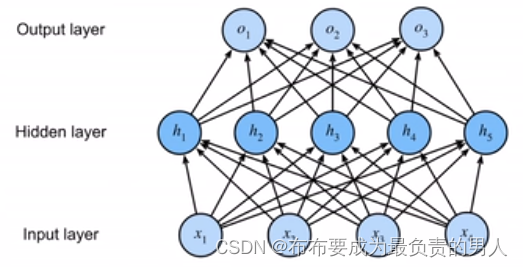
其中,隐藏层的大小是超参数。隐藏层的相关内容将在后面详细介绍。
隐藏层
对于之前的线性回归模型,标签通过仿射变换以后,确实与我们的输入数据直接相关了,所以无需隐藏层。但是,仿射变换中的线性其实是一种太过于强的假设了。
线性模型可能会出错
线性模型意味着单调:任何特征的增大都会导致模型输出的增大或缩小(取决于对应的权重符号)。
然而我们能找出很多违反单调性的例子。例如,我们想要根据体温预测死亡率。对体温高于37摄氏度的人来说,温度越高风险越大。然而,对体温低于37摄氏度的人来说,温度越高风险就越低。
再比如,上一节中我们对猫狗图像进行分类,如果用线性模型,区分猫和狗的唯一要求变为了评估单个像素的强度。在一个倒置图像后依然保留类别的世界里,注定失败。
这是因为,任何像素的重要性都以复杂的方式取决于该像素的上下文(周围像素的值)。由于这会考虑到特征之间的相关交互作用,所以我们引入了隐藏层。
在网络中加入隐藏层
我们可以在网络中加入一个或多个隐藏层来克服线性模型的限制,使其可以处理更普遍的函数关系类型。要做到这一点,最简单的方法是将许多全连接层都堆叠到一起,每一层都输出到上面的层,直到生成最后的输出。
我们可以把前L-1层都看作是表示,把最后一层看作是线性预测器。这种架构就叫做多层感知机,缩写为MLP
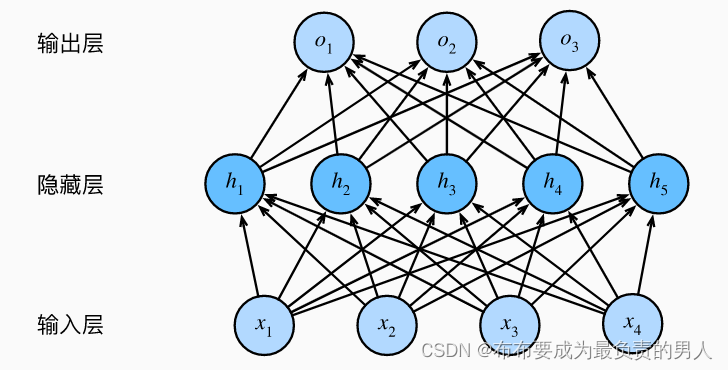
如该图为一个单隐藏层的多层感知机,具有5个隐藏单元。输入层不涉及任何计算,因此使用此网络产生输出只需要实现隐藏层和输出层的计算。
因此,该MLP的层数为2,。注意,这两个层都是全连接的,每个输入都会影响隐藏层的每个神经元,而隐藏层中的每个神经元又会影响输出层中的每个神经元。
从线性到非线性
我们通过矩阵X表示n个样本的小批量,其中每个样本都具有d个输入特征。对于具有h个隐藏单元的单隐藏层多层感知机,用H表示隐藏层的输出,称为隐藏表示。我们用如下方式计算单隐藏层多层感知机的输出O:
H = X W ( 1 ) + b ( 1 ) O = H W ( 2 ) + b ( 2 ) H=XW^{(1)}+b^{(1)}\\ O=HW^{(2)}+b^{(2)} H=XW(1)+b(1)O=HW(2)+b(2)
其实,如果只是上面的式子,并没有改变线性模型的情况。我们试着合并一下单隐藏层,可得:
O = ( X W ( 1 ) + b ( 1 ) ) W ( 2 ) + b ( 2 ) = X W ( 1 ) W ( 2 ) + b ( 1 ) W ( 2 ) + b ( 2 ) O=(XW^{(1)}+b^{(1)})W^{(2)}+b^{(2)}=XW^{(1)}W^{(2)}+b^{(1)}W^{(2)}+b^{(2)} O=(XW(1)+b(1))W(2)+b(2)=XW(1)W(2)+b(1)W(2)+b(2)
上式其实也只有X是未知的,那么上式其实就可以等价于O=XW+b了。
因此,为了发挥出多层架构的潜力,我们需要引入激活函数σ。激活函数的输出称为活性值。一般来说,只要有了激活函数,就不可能再将我们的多层感知机退化成线性模型:
H = σ ( X W ( 1 ) + b ( 1 ) ) , O = H W ( 2 ) + b ( 2 ) H=\sigma(XW^{(1)}+b^{(1)}),\\ O=HW^{(2)}+b^{(2)} H=σ(XW(1)+b(1)),O=HW(2)+b(2)
通用近似定理
多层感知机可以通过隐藏神经元,捕捉到输入之间复杂的相互作用,这些神经元依赖于每个输入的值。
我们可以很容易地设计隐藏结点从而执行任意计算。例如在一对输入上进行基本逻辑操作,多层感知机是通用近似器。即使是网络只有一个隐藏层,给足足够的神经元和正确的权重,我们可以对任意函数建模。
虽然一个单隐藏层可以学习任何函数,但是不代表通过一个单隐藏层就可以解决所有问题,事实上通过更深的网络,可以更容易的逼近许多函数。
激活函数
前面已经讲过了激活函数的必要性,它是线性模型转换为非线性模型的关键。激活函数通过计算加权和并加上偏置来确定神经元是否应该被激活,它们将输入信号转换为输出的可微运算。大多数激活函数都是非线性的。
import torch
from d2l import torch as d2l
ReLU函数
实现简单且最受欢迎的激活函数,就是修正线性单元(ReLU),它提供了一种非常简单的非线性变化:
R e L U ( x ) = m a x ( x , 0 ) ReLU(x)=max(x,0) ReLU(x)=max(x,0)
通俗的说,ReLU函数将对应的活性值设为0,仅保留正元素并丢弃所有负元素。我们可以画出函数的曲线图:
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))
d2l.plt.show()
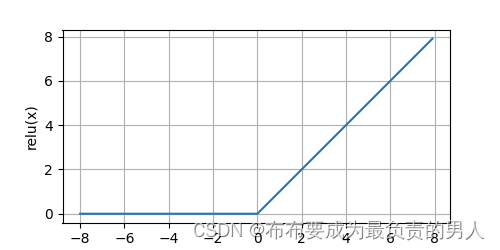
我们可以绘制ReLU函数的导数:
y.backward(torch.ones_like(x), retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))
d2l.plt.show()
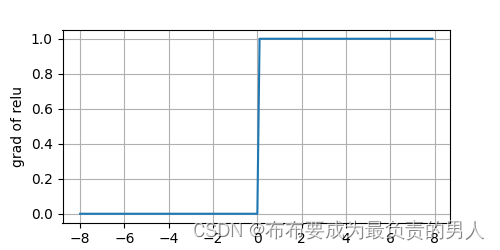
选用ReLU的原因:它求导表现的很好,要么让参数消失,要么让参数通过。这使得优化表现得更好,并且ReLU减轻了困扰以往神经网络的梯度消失问题。
而ReLU也有很多变体,如参数化ReLU函数,其添加了一个线性项,因此即使参数是负的,某些信息仍然可以通过:
p R e L U ( x ) = m a x ( 0 , x ) + α m i n ( 0 , x ) pReLU(x)=max(0,x)+αmin(0,x) pReLU(x)=max(0,x)+αmin(0,x)
sigmoid函数
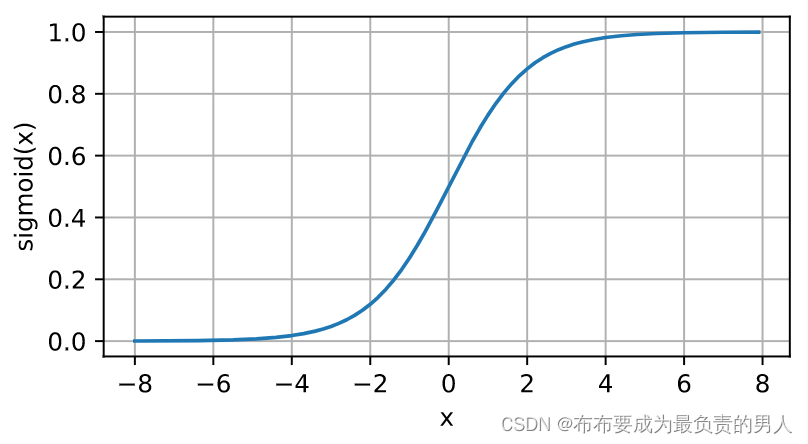
sigmoid函数将输入变换为区间(0,1)上输出,因此通常称为挤压函数:
s i g m o i d ( x ) = 1 1 + e − x sigmoid(x)=\frac{1}{1+e^{-x}} sigmoid(x)=1+e−x1
tanh函数
和sigmoid类型,双曲正切函数也是压缩区间,压缩到了(-1,1):
t a n h ( x ) = 1 − e − 2 x 1 + e − 2 x tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}} tanh(x)=1+e−2x1−e−2x
多类分类
其实就是之前的softmax函数加了个隐藏层:
输入 x ∈ R n 隐藏层 W 1 ∈ R m × n , b 1 ∈ R m 输出层 W 2 ∈ R m × k , b 2 ∈ R k 输入x∈R^n\\ 隐藏层W_1∈R^{m×n},b_1∈R^m\\ 输出层W_2∈R^{m×k},b_2∈R^k\\ 输入x∈Rn隐藏层W1∈Rm×n,b1∈Rm输出层W2∈Rm×k,b2∈Rk
那么可以得到:
h = σ ( W 1 x + b 1 ) o = W 2 T h + b 2 y = s o f t m a x ( o ) h=\sigma(W_1x+b_1)\\ o=W_2^Th+b_2\\ y=softmax(o) h=σ(W1x+b1)o=W2Th+b2y=softmax(o)
注意这里的o的表达式和之前写的不一样,上面只是给出个大概,而真正要进行运算的时候要满足矩阵乘法的原则:前面的列数等于后面的行数。
相关文章:

机器学习深度学习——多层感知机
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——感知机 📚订阅专栏:机器学习&&深度学习 希望文章对你们有所帮助 上一节…...

Django模型将模型注释同步到数据库
1、安装django-comment-migrate库 pip install django-comment-migrate 2、将库注册到settings.py文件中 INSTALLED_APPS [...django_comment_migrate, # 表注释... ] 3、加注释 3.1、给模型(表)加注释 在模型的class Meta中编辑 verbose_name&…...
)
STM32 Flash学习(二)
STM32F1的官方固件库操作FLASH的几个常用函数。这些函数和定义分布在源文件stm32f1xx_hal_flash.c/stm32f1xx_hal_flash_ex.c以及头文件stm32f1xx_hal_flash.h/stm32f1xx_hal_flash_ex.h中。 锁定解函数 对FLASH进行写操作前必须先解锁,解锁操作:在FLA…...

kotlin获取泛型集合的类型信息
通过 reified 关键字和内联函数来实现 inline fun <reified T> getClassFromList(list: List<T>): Class<T> {return T::class.java }fun main() {val list listOf("Hello", "World")val clazz getClassFromList(list)println(clazz)…...

AQS源码解析
关于 AQS,网上已经有无数的文章阐述 AQS 的使用及其源码,所以多这么一篇文章也没啥所谓,还能总结一下研究过的源码。源码解析和某某的使用,大概是互联网上 Java 文章中写得最多的主题了。 AQS AQS 是 AbstractQueuedSynchronize…...

关于在VS2017中编译Qt项目遇到的问题
关于在VS2017中编译Qt项目遇到的问题 【QT】VS打开QT项目运行不成功 error MSB6006 “cmd.exe”已退出,代码为 2。如何在VS2017里部署的Qt Designer上编辑槽函数 【QT】VS打开QT项目运行不成功 error MSB6006 “cmd.exe”已退出,代码为 2。 链接 如何在VS2017里部署的Qt Design…...

Python web实战 | 使用 Flask 实现 Web Socket 聊天室
概要 今天我们学习如何使用 Python 实现 Web Socket,并实现一个实时聊天室的功能。本文的技术栈包括 Python、Flask、Socket.IO 和 HTML/CSS/JavaScript。 什么是 Web Socket? Web Socket 是一种在单个 TCP 连接上进行全双工通信的协议。它是 HTML5 中的…...
隐藏recovery菜单项)
Android10 Recovery系列(一)隐藏recovery菜单项
一 、背景 起因是遇到了一个隐藏删除recovery菜单项的需求。在寻找解决问题的时候,我经历了找到源码位置,调试修改,生效,思考是否可拓展,优化修改,符合要求的整个过程,下面简单分享一下。如果不想立即实现效果或者只想看解决方案,可以直接看总结那一个部分 二 、准备…...
选好NAS网络储存解决方案,是安全储存的关键
随着网络信息的发展,NAS也越来越受到企业的关注,NAS网络存储除了提供简单的存储服务外,还可以提供更好的数据安全性、更方便的文件共享方式。但市面上的产品种类繁多,我们该如何选择合适的产品,通过企业云盘࿰…...

AnimateDiff论文解读-基于Stable Diffusion文生图模型生成动画
文章目录 1. 摘要2. 引言3. 算法3.1 Preliminaries3.2. Personalized Animation3.3 Motion Modeling Module 4. 实验5.限制6. 结论 论文: 《AnimateDiff: Animate Your Personalized Text-to-Image Diffusion Models without Specific Tuning》 github: https://g…...
centos7安装tomcat
安装tomcat 必须依赖 JDK 环境,一定要提前装好JDK保证可以使用 一、下载安装包 到官网下载 上传到linux 服务器 二、安装tomcat 创建tomcat 文件夹 mkdir -p /usr/local/tomcat设置文件夹权限 chmod 757 tomcat将安装包上传至 新建文件夹 解压安装包 tar zx…...
【C#教程】零基础从入门到精通
今天给大家分享一套零基础从入门到精通:.NetCore/C#视频教程;这是2022年最新整理的、590G的开发教程资料。课程涵盖了.Net各方面的知识,跟着这个教程学习,就足够了。 课程分类 1、C#从基础到精通教程; 2、Winform从…...

opencv rtsp 硬件解码
讨论使用opencv的reader 硬件解码的方案有太多种,如果使用ffmpeg硬件解码是最方便的,不方便的是把解码过后的GPU 拉到 CPU 上,再使用opencv的Mat 从cpu 上上载到gpu上,是不是多了两个过程,应该是直接从GPU mat 直接去…...

机器学习-Gradient Descent
机器学习(Gradient Descent) videopptblog 梯度下降(Gradient Descent) optimization problem: 损失函数最小化 假设本模型有两个参数𝜃1和𝜃2,随机取得初始值 求解偏微分,梯度下降对参数进行更新 Visualize: 确定梯度方向&…...
基础知识)
MySql003——SQL(结构化查询语言)基础知识
一、数据库的相关概念 DB:数据库(Database) 即存储数据的“仓库”,其本质是一个文件系统。它保存了一系列有组织的数据。DBMS:数据库管理系统(Database Management System) 是一种操纵和管理数…...

springCloud Eureka注册中心配置详解
1、创建一个springBoot项目 2、在springBoot项目中添加SpringCloud依赖 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-dependencies</artifactId><version>2021.0.3</version><type>…...
gti 远程操作
目录 一. 分布式版本控制管理系统 1. 理解分布式版本控制管理系统 二. 创建远程仓库 编辑 编辑 三. 克隆远程仓库_HTTP 四. 克隆远程仓库_SSH 配置公钥 添加公钥 五. git 向远程仓库推送 六. 拉取远程仓库 七. 忽略特殊文件 八. 配置别名 一. 分布式版本控制管理…...

Ftrace
一、概述 Ftrace有剖析器和跟踪器。剖析器提供统计摘要,如激素胡和直方图;而跟踪器提供每一个事件的细节。 Ftrace剖析器列表: 剖析器描述function内核函数统计分析kprobe profiler启用的kprobe计数器uprobe profiler启用的uprobe计数器hi…...
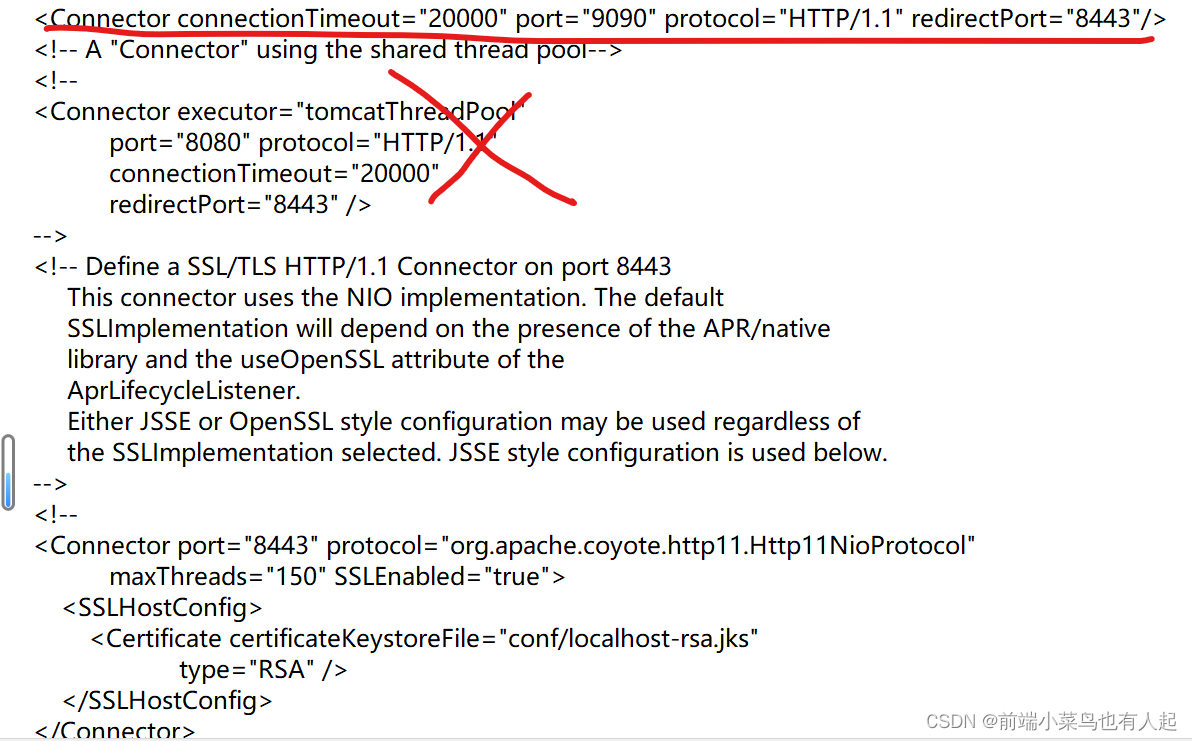
Tomcat修改端口号
网上的教程都比较老,今天用tomcat9.0记录一下 conf文件夹下server.xml文件 刚开始改了打红叉的地方,发现没用,改了上面那行...
)
vue2企业级项目(一)
vue2企业级项目(一) 创建项目,并创建项目编译规范 1、node 版本 由于是vue2项目,所以 node 版本比较低。使用 12.18.3 左右即可 2、安装vue 安装指定版本的vue2 npm i -g vue2.7.10 npm i -g vue/cli4.4.63、编辑器规范 vsc…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...

大模型真的像人一样“思考”和“理解”吗?
Yann LeCun 新研究的核心探讨:大语言模型(LLM)的“理解”和“思考”方式与人类认知的根本差异。 核心问题:大模型真的像人一样“思考”和“理解”吗? 人类的思考方式: 你的大脑是个超级整理师。面对海量信…...

react-pdf(pdfjs-dist)如何兼容老浏览器(chrome 49)
之前都是使用react-pdf来渲染pdf文件,这次有个需求是要兼容xp环境,xp上chrome最高支持到49,虽然说iframe或者embed都可以实现预览pdf,但为了后续的定制化需求,还是需要使用js库来渲染。 chrome 49测试环境 能用的测试…...
