机器学习-Gradient Descent
机器学习(Gradient Descent)
| video | ppt | blog |
|---|
梯度下降(Gradient Descent)
optimization problem:

损失函数最小化
假设本模型有两个参数𝜃1和𝜃2,随机取得初始值
求解偏微分,梯度下降对参数进行更新
Visualize:
确定梯度方向,红色表示Gradient方向,蓝色是梯度下降的方向,因为我们要是损失函数L减小,使用应该取与Gradient方向相反的方向,这也对应着进行参数更新时用的是
-(减号)
其中:η 叫做Learning rates(学习速率)

Small Tips
Tip 1:Tuning your learning rates
下面是两幅图,我们来简单看一下
- 图左边黑色为损失函数的曲线,假设从左边最高点开始:(一维)
- 学习率刚刚好,比如红色的线,就能顺利找到最低点。
- 学习率太小,比如蓝色的线,也可以顺利找到最低点,就会走的太慢,时间成本太高。
- 学习率有点大,比如绿色的线,出现了跳过最低点,反复进行横跳,很难到达最低点。
- 学习率非常大,比如黄色的线,直接就飞出去了,更新参数的时候只会发现
损失函数越更新越大。- 当参数为一维或者二维的时候,我们可以很直观地建立图形进行观察,但是超过了三维以后,我们就无法进行可视化,但是右图是始终可以建立的,分别表示了不同学习率下参数更新以后损失函数的变化情况。将参数改变对损失函数的影响进行可视化。比如学习率太小(蓝色的线),损失函数下降的非常慢;学习率太大(绿色的线),损失函数下降很快,但马上就卡住不下降了;学习率特别大(黄色的线),损失函数就飞出去了;红色的就是差不多刚好,可以得到一个好的结果。

我们可能会猜想,学习率很重要,既不能太大,跳出最优解,也不能太小,收敛过慢,那有没有一种可能实现学习率地改变呢?
Adaptive Learning Rates
在训练的过程中,我们需要实现学习率的自适应变化:
- Reduce the learning rate by some factor every few epochs.
- 前期初始点可能距离最低点较远,我们可以将学习率设置大一些,使得损失函数更快收敛。
- update参数以后,离最低点较近,此时,我们应该调整学习率变小,防止跳过了最低点。
- Learning rate cannot be one-size-fits-all
- 给不同的参数分配不同的学习率
自适应学习率算法-Adagrad
下面有两种方法,第一种是针对一个参数的,但是我们要学习的是第二种,实现参数独立的自适应学习率算法

w是一个参数
𝜎t :之前参数的所有微分的均方根,对于每个参数都是不一样的。
普通梯度下降如Vanilla Gradient descent
使用Adagrad算法:每个参数的学习率都把除以之前微分的均方根。

变形
Contradiction
按照正常的理解,梯度越大,说明可能离最低点越远,那么我们变化的步伐也应该越大,梯度越小,说明可能离最低点越远,那么我们变化的步伐也应该越小,但是在Adagrad算法里面,当梯度越大的时候,步伐应该越大,但下面分母又导致当梯度越大的时候,步伐会越小,前后有点矛盾了。
解释:
此处我们的步长是相对的,我们当前的梯度的大小也是相对于前面的梯度大小来调整步长
- 构造反差效果
- 通过实例看出最优步长与一次微分成正比,与二次微分成反比,这里采用之前所有一次微分的均方根估计二次微分
- 正比解释:一次微分越大,说明可能离最低点越远,步伐越大
- 反比解释:二次微分越小,一次微分变化越慢,一次微分也就倾向于保留较大的趋势,步伐也就越大
- 同一参数,可以通过比较其一次微分比较其距离最优值的距离;不同参数还需要考虑二次微分。
Do not cross parameters
- 第2点我们提到了Use first derivative to estimate second derivative
- 一个较为复杂的参数模型,我们在进行求解的时候,算一次偏微分可能就需要很长的时间,所以二次偏微分一般不可取
- 一般情况下,在一定的范围内取一次偏微分,进行平方求和开根号,在一定的程度上面也可以反映二次偏微分的大小
Tip 2:Stochastic Gradient Descent(SGD)
基本思想:损失函数没处理一个批次的数据就进行一次更新,
- 普通的算法在进行参数更新的时候是一次遍历所有的例子,然后更新,实现一次更新,步伐一般较大。
- SGD算法进行参数更新的时候每遍历一个例子就进行一次更新,实现多次更新,一般步伐较小。
Tip 3:Feature Scaling

存在多个变量的时候,很可能出现的一种情况就是,他们的取值范围不一样,一个可以很大,一个可以很小,那么我们在对他们的对应参数进行相同变化的时候,而y的变化的情况却大不相同。

左图: x1的scale比x2要小很多,所以当 w1和 w2做同样的变化时,w1对 y 的变化影响是比较小的(w1对损失函数L有较小的微分,在w1方向上梯度较小,图像较为平滑),x2 对 y 的变化影响是比较大的(w2对损失函数L有较大的微分,在w2方向上梯度较大,图像上有比较陡峭的峡谷)
右图:二者scale相近,各点处梯度大致相同
来源
Normalize

计算每一个维度变量的
- 均值:mi
- 标准差: σi
进行相应的变化
这样所有维度的均值都是0,方差都是1。
Gradient Descent Theory
当我们在使用梯度下降算法进行参数优化的时候,每一次的优化并不能百分百保证使得损失函数越来越小。

我们在一般情况下,我们无法一瞬间找到全局最优解,可以做到的是给定某个初始值和某个范围,我们可以找到局部最低点。
How to y find the point with the smallest value nearby?
Taylor Series
一个变量的泰勒展开

Taylor多项式在点x=x0上逼近函数的值。多项式的阶次越高,多项式中的项越多,逼近函数的实际值越近。

两个变量的泰勒展开

Gradient Desent

我们在前面提到了,给定某个初始值和某个范围,如果这个范围足够小,那么我们是不是可以用泰勒展开对损失函数表达式进行替换

以d为半径,做一个足够小的圆形区域,在这个区域上面,我们可以使用泰勒展开

s可以看作定值,后面可以看作
向量点乘(不记得的去百度一下)
点乘还有一种计算方法就是:两向量的模相乘再乘以夹角的余弦值,其中(u,v)是一节偏微分,是梯度,所以要让点乘结果最小,我们可以让两向量方向相反,夹角余弦值为-1,让另一向量模最大,但是有边界限制。

现在我们可以更好理解使用泰勒展开的意义了,最后得到的向量的方向也就是我们向最低点移动的方向,但是不要忘记了我们使用泰勒展开的前提
范围足够小,同样也要求我们学习率也要足够小,这样才能保证泰勒展开的精度是足够的
More Limitation of Gradient Descent
- 微分值为0,可能是极值点,但不一定是全局极值,也可能仅仅只是微分值为0的非极值点
- 在实际的ML中,当微分值小于某一个数值就停下来了,但这里只是比较平缓,并不是极值点

相关文章:

机器学习-Gradient Descent
机器学习(Gradient Descent) videopptblog 梯度下降(Gradient Descent) optimization problem: 损失函数最小化 假设本模型有两个参数𝜃1和𝜃2,随机取得初始值 求解偏微分,梯度下降对参数进行更新 Visualize: 确定梯度方向&…...
基础知识)
MySql003——SQL(结构化查询语言)基础知识
一、数据库的相关概念 DB:数据库(Database) 即存储数据的“仓库”,其本质是一个文件系统。它保存了一系列有组织的数据。DBMS:数据库管理系统(Database Management System) 是一种操纵和管理数…...

springCloud Eureka注册中心配置详解
1、创建一个springBoot项目 2、在springBoot项目中添加SpringCloud依赖 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-dependencies</artifactId><version>2021.0.3</version><type>…...
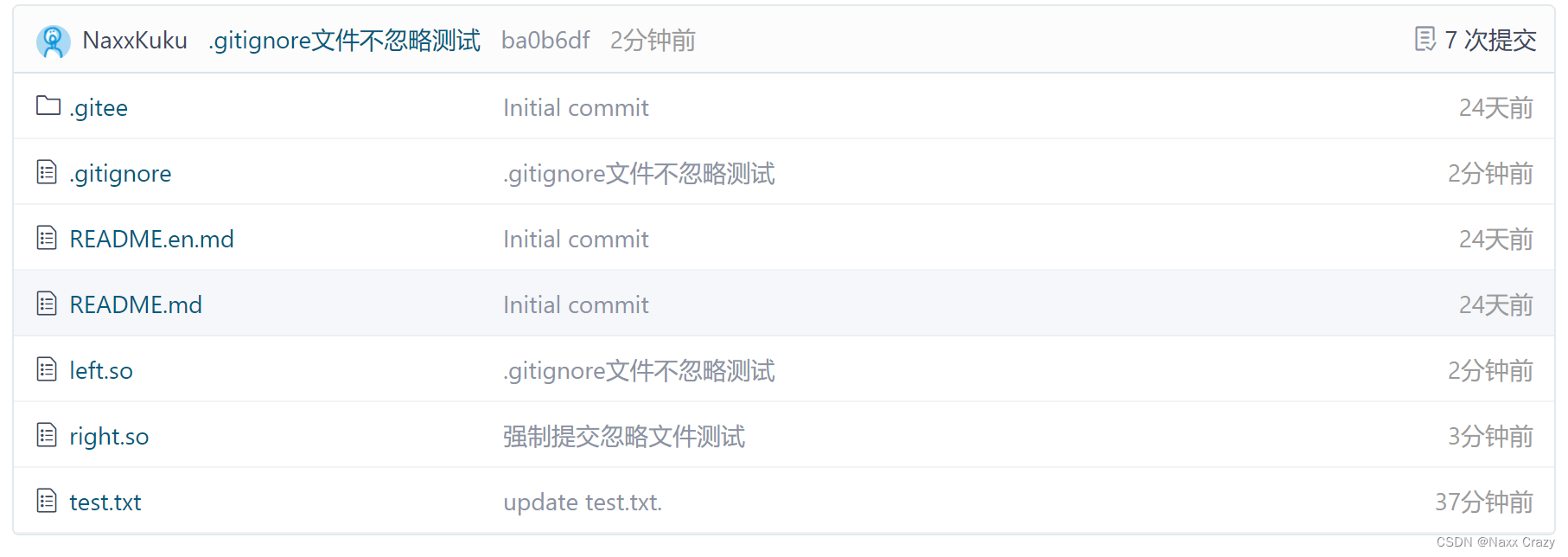
gti 远程操作
目录 一. 分布式版本控制管理系统 1. 理解分布式版本控制管理系统 二. 创建远程仓库 编辑 编辑 三. 克隆远程仓库_HTTP 四. 克隆远程仓库_SSH 配置公钥 添加公钥 五. git 向远程仓库推送 六. 拉取远程仓库 七. 忽略特殊文件 八. 配置别名 一. 分布式版本控制管理…...

Ftrace
一、概述 Ftrace有剖析器和跟踪器。剖析器提供统计摘要,如激素胡和直方图;而跟踪器提供每一个事件的细节。 Ftrace剖析器列表: 剖析器描述function内核函数统计分析kprobe profiler启用的kprobe计数器uprobe profiler启用的uprobe计数器hi…...
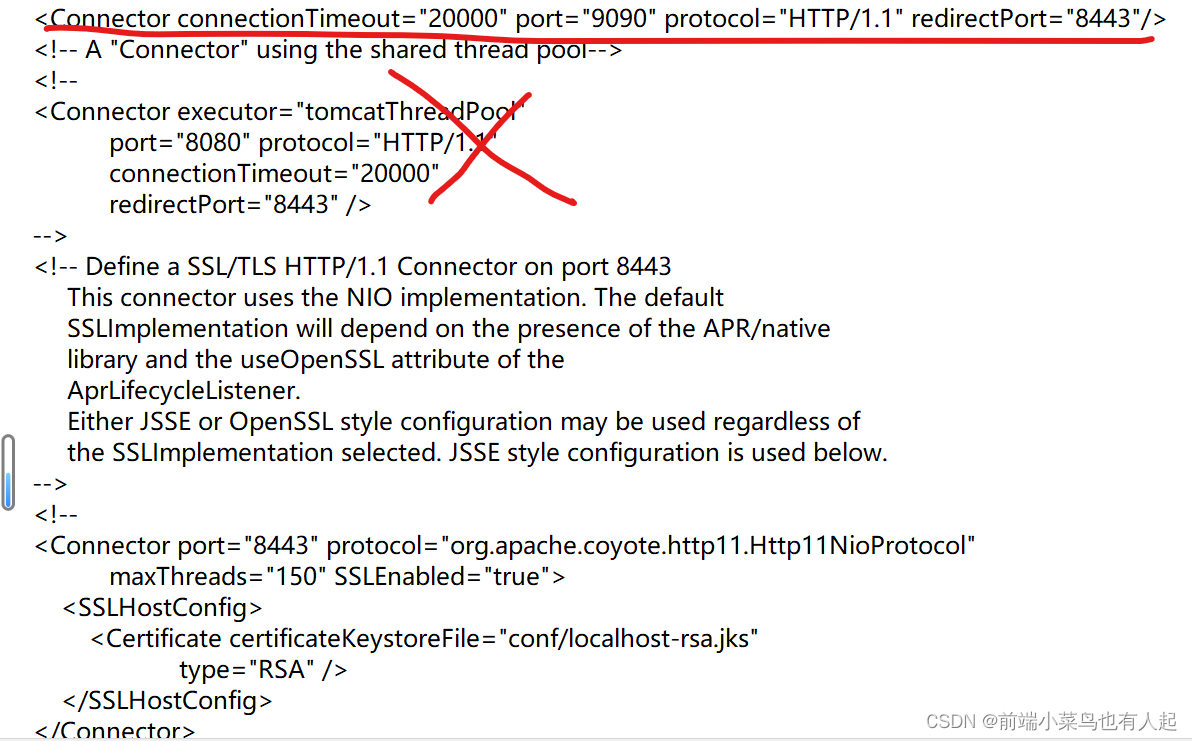
Tomcat修改端口号
网上的教程都比较老,今天用tomcat9.0记录一下 conf文件夹下server.xml文件 刚开始改了打红叉的地方,发现没用,改了上面那行...
)
vue2企业级项目(一)
vue2企业级项目(一) 创建项目,并创建项目编译规范 1、node 版本 由于是vue2项目,所以 node 版本比较低。使用 12.18.3 左右即可 2、安装vue 安装指定版本的vue2 npm i -g vue2.7.10 npm i -g vue/cli4.4.63、编辑器规范 vsc…...
——log、thunk、applyMiddleware中间件的核心代码)
【前端知识】React 基础巩固(三十八)——log、thunk、applyMiddleware中间件的核心代码
React 基础巩固(三十八)——log、thunk、applyMiddleware中间件的核心代码 一、打印日志-中间件核心代码 利用Monkey Patching,修改原有的程序逻辑,在调用dispatch的过程中,通过dispatchAndLog实现日志打印功能 // 打印日志-中间件核心代码…...

hive删除数据进行恢复
在实际开发或生产中,hive表如果被误删,如被truncate或是分区表的分区被误删了,只要在回收站的清空周期内,是可以恢复数据的,步骤如下: (1) 先找到被删除数据的存放目录,…...
二、前端高德地图、渲染标记(Marker)引入自定义icon,手动设置zoom
要实现这个效果,我们先看一下目前的页面展示: 左边有一个图例,我们可以方法缩小地图,右边是动态的marker标记,到时候肯定时候是后端将对应的颜色标识、文字展示、坐标点给咱们返回、我们肯定可以拿到一个list…...

UDF和UDAF、UDTF的区别
UDF UDF(User-defined functions)用户自定义函数,简单说就是输入一行输出一行的自定义算子。 是大多数 SQL 环境的关键特性,用于扩展系统的内置功能。(一对一) UDAF UDAF(User Defined Aggregat…...

小研究 - 浅析 JVM 中 GC 回收算法与垃圾收集器
本文主要介绍了JVM虚拟机中非常重要的两个部分,GC 回收算法和垃圾收集器。从可回收对象的标记开始,详细介绍 了四个主流的GC算法,详细总结了各自的算法思路及优缺点, 提出了何种情况下应该通常选用哪种算法。 目录 1 标记可回收对…...

Flowable-服务-骆驼任务
目录 定义图形标记XML内容Flowable与Camel集成使用示例设计Came路由代码 定义 Camel 任务不是 BPMN 2.0 规范定义的官方任务,在 Flowable 中,Camel 任务是作为一种特殊的服务 任务来实现的。主要做路由工作的。 图形标记 由于 Camel 任务不是 BPMN 2.…...

用html+javascript打造公文一键排版系统9:主送机关排版
一、主送机关的规定 公文一般在标题和正文之间还有主送机关,相关规定为: 主送机关 编排于标题下空一行位置,居左顶格,回行时仍顶格,最后一个机关名称后标全角冒号。如主送机关名称过多导致公文首页不能显示正文时&…...
SpringBoot 集成 EasyExcel 3.x 优雅实现 Excel 导入导出
介绍 EasyExcel 是一个基于 Java 的、快速、简洁、解决大文件内存溢出的 Excel 处理工具。它能让你在不用考虑性能、内存的等因素的情况下,快速完成 Excel 的读、写等功能。 EasyExcel文档地址: https://easyexcel.opensource.alibaba.com/ 快速开始 …...
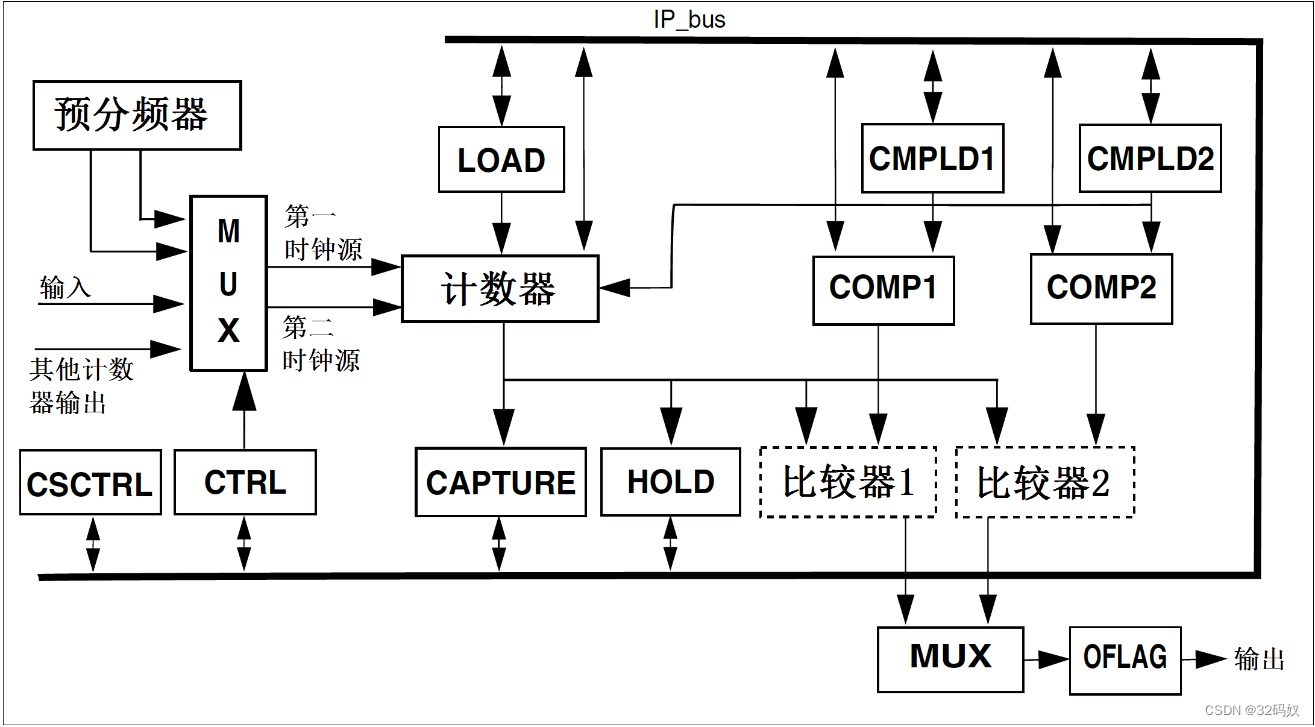
RT1052 的四定时器
文章目录 1 Quad Timer,简称:QTMR2 单个通道的框图3 QTMR配置3.1 QTMR1 时钟使能。3.2 初始化 QTMR1。3.2.1 QTMR_Init 3.3 设置 QTMR1 通道 0 的定时周期。3.3.1QTMR_SetTimerPeriod 3.4 使能 QTMR1 通道 0 的比较中断。3.4.1 QTMR_EnableInterrupts 3.…...

ViT-vision transformer
ViT-vision transformer 介绍 Transformer最早是在NLP领域提出的,受此启发,Google将其用于图像,并对分类流程作尽量少的修改。 起源:从机器翻译的角度来看,一个句子想要翻译好,必须考虑上下文的信息&…...

Election of the King 2023牛客暑期多校训练营4-F
登录—专业IT笔试面试备考平台_牛客网 题目大意:有一个n个数的数组a,有n-1轮操作,每轮由每个数选择一个和它的差最大的数,如果相同就选值更大的,被最多数组选择的数字被删去,有相同的也去掉数值更大的那个…...
Nacos的搭建及服务调用
文章目录 一、搭建Nacos服务1、Nacos2、安装Nacos3、Docker安装Nacos 二、OpenFeign和Dubbo远程调用Nacos的服务1、搭建SpringCloudAlibaba的开发环境1.1 构建微服务聚合父工程1.2 创建子模块cloud-provider-payment80011.3 创建子模块cloud-consumer-order80 2、远程服务调用O…...
uniapp小程序自定义loding,通过状态管理配置全局使用
一、在项目中创建loding组件 在uniapp的components文件夹下创建loding组件,如图: 示例代码: <template><view class"loginLoading"><image src"../../static/loading.gif" class"loading-img&q…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

GraphRAG优化新思路-开源的ROGRAG框架
目前的如微软开源的GraphRAG的工作流程都较为复杂,难以孤立地评估各个组件的贡献,传统的检索方法在处理复杂推理任务时可能不够有效,特别是在需要理解实体间关系或多跳知识的情况下。先说结论,看完后感觉这个框架性能上不会比Grap…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...









