day52|● 300.最长递增子序列 ● 674. 最长连续递增序列 ● 718. 最长重复子数组
300.最长递增子序列
Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.
这题看似简单,但感觉没想明白递增的判定(当前下标i的递增子序列长度,其实和i之前的下表j的子序列长度有关系)和递推的关系
“子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序”。注意 这里是找递增子序列,他的递增可以是不连续的。
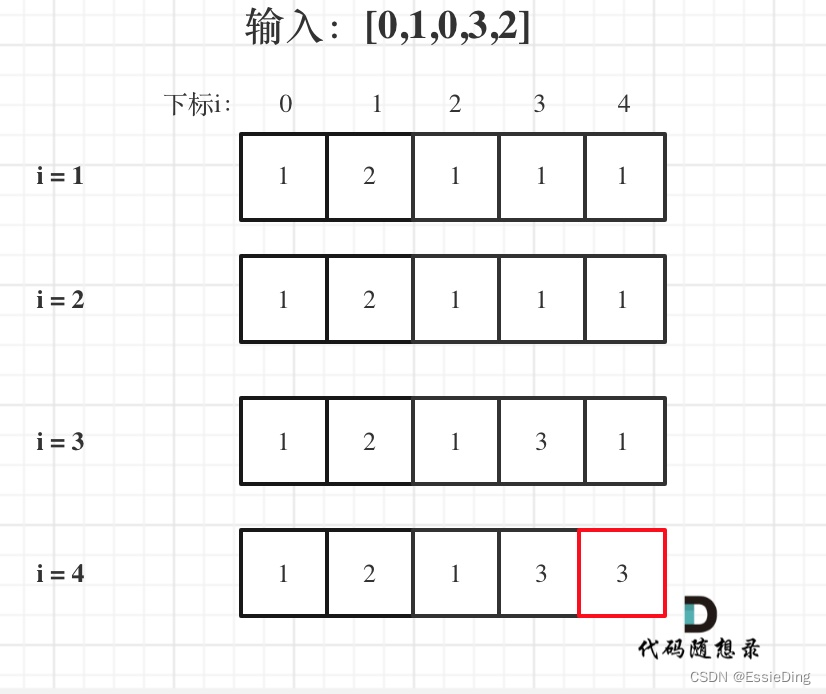
dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度
注意是以nums[i]结尾,和nums[j]比较(j在0到i之间),取最大的长度值
并非dp[i] 与 dp[j] + 1进行比较,而是我们要取dp[j] + 1的最大值。
需要把视角抽离出来,发现要求到当前i位置的最长递增子序列,其实依靠的是到他之前所有递增子序列长度的最大值,重点在[0 : i) 之前的所有dp
class Solution {public int lengthOfLIS(int[] nums) {// dp[i] the length of the longest increasing subsequence ending with nums[i]// dp[i]是以nums[i]为子序列尾元素的最长递增子序列的长度int[] dp = new int[nums.length];for (int i = 0; i < dp.length; i++) {dp[i] = 1;}int maxLength = 1;for (int i = 1; i < nums.length; i++) {for (int j = 0; j < i; j++) { // 着重注意理解这个forif (nums[i] > nums[j]){dp[i] = Math.max(dp[i], dp[j]+1);}}maxLength = dp[i] > maxLength ? dp[i]:maxLength;}return maxLength;}
}
时间复杂度: O(n^2)
空间复杂度: O(n)
674. 最长连续递增序列
dp[i]:以下标i为结尾的连续递增的子序列长度为dp[i]。
因为本题要求连续递增子序列,所以就只要比较nums[i]与nums[i - 1],而不用去比较nums[j]与nums[i] (j是在0到i之间遍历)。
既然不用j了,那么也不用两层for循环,本题一层for循环就行,比较nums[i] 和 nums[i - 1]。
class Solution {public int findLengthOfLCIS(int[] nums) {int[] dp = new int[nums.length];for (int i = 0; i < nums.length; i++) {dp[i] = 1;}int res = 1;for (int i = 1; i < nums.length; i++) {if (nums[i] > nums[i-1]) {dp[i] = dp[i-1]+1;}res = Math.max(res, dp[i]);}return res;}
}
时间复杂度:O(n)
空间复杂度:O(n)
718. 最长重复子数组
dp[i][j] :以下标i 为结尾的nums1,和以下标j 为结尾的nums2,最长重复子数组长度为dp[i][j]。
(特别注意: “以下标i 为结尾的A” 标明一定是 以A[i]为结尾的字符串 )
class Solution {public int findLength(int[] nums1, int[] nums2) {int[][] dp = new int[nums1.length][nums2.length];int maxLength = 0;for (int i = 0; i < nums1.length; i++) {for (int j = 0; j < nums2.length; j++) {if (nums1[i] == nums2[j]) {if (i==0 || j==0) {dp[i][j] = 1;} else {dp[i][j] = dp[i-1][j-1]+1;}}maxLength = Math.max(maxLength, dp[i][j]);}}return maxLength;}
}
相关文章:

day52|● 300.最长递增子序列 ● 674. 最长连续递增序列 ● 718. 最长重复子数组
300.最长递增子序列 Input: nums [10,9,2,5,3,7,101,18] Output: 4 Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4. 这题看似简单,但感觉没想明白递增的判定(当前下标i的递增子序列长度,其实…...

uniapp,vue3路由传递接收参数
官网vue2升vue3的教程中,演示了如何使用onLoad,记得把官网所有内容都看一遍!!! 传递对象参数 uni.navigateTo({url: /pages/login/code/code?data JSON.stringify({limit: 6, iphone: loginForm.username, }), });…...
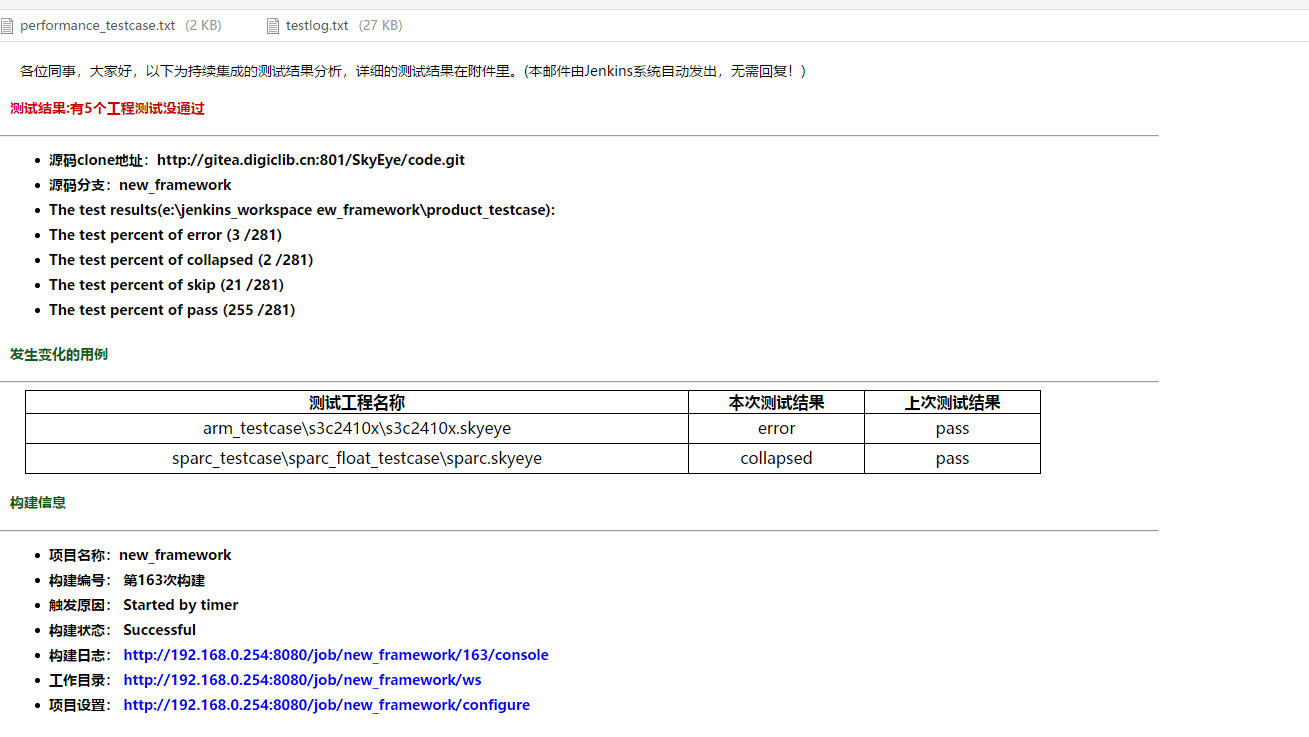
SkyEye与Jenkins的DevOps持续集成解决方案
在技术飞速发展的当下,随着各行各业的软件逻辑复杂程度提升带来的需求变更,传统测试已无法满足与之相对应的一系列测试任务,有必要引入一个自动化、可持续集成构建的DevOps平台来解决此类问题。本文将主要介绍SkyEye与Jenkins的持续集成解决方…...

HCIE Security——防火墙互联技术
目录 一、防火墙接口互联接口 1.防火墙支持的接口及板卡 2.物理链接线缆 3.支持接口种类 (1)物理接口 (2)逻辑接口 二、相关配置命令 1.配置三层接口IP地址 2.配置PPPOE拨号接口 3.配置VLANIF接口、子接口、回环接口 4…...

Rust- 闭包
A closure in Rust is an anonymous function you can save in a variable or pass as an argument to another function. You can create the closure using a lightweight syntax and access variables from the scope in which it’s defined. Here’s an example of a clo…...
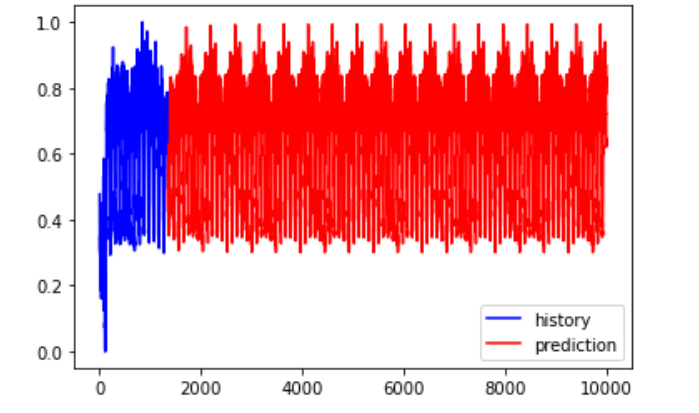
【数据挖掘torch】 基于LSTM电力系统负荷预测分析(Python代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

「JVM」性能调优工具
「JVM」性能调优工具 一、jcmd1、jcmd 能干嘛?2、与JVM相关的命令3、示例 二、jmap1、jmap有什么用?2、jmap的命令大全3、示例 三、jps1、jps有什么用?2、jps命令以及示例 四、jstat1、jstat有什么用?2、jstat命令以及示例 五、js…...
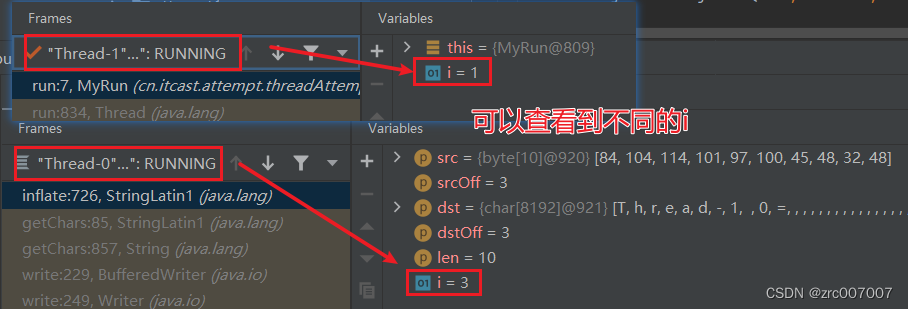
IDEA Debug小技巧 添加减少所查看变量、查看不同线程
问题 IDEA的Debug肯定都用过。它下面显示的变量,有什么门道?可以增加变量、查看线程吗? 答案是:可以。 演示代码 代码如下: package cn.itcast.attempt.threadAttempt.attempt2;public class Test {public static …...

基于SpringBoot+Vue的车辆充电桩管理系统设计与实现(源码+LW+部署文档等)
博主介绍: 大家好,我是一名在Java圈混迹十余年的程序员,精通Java编程语言,同时也熟练掌握微信小程序、Python和Android等技术,能够为大家提供全方位的技术支持和交流。 我擅长在JavaWeb、SSH、SSM、SpringBoot等框架…...

Bean的加载方式
目录 1. 基于XML配置文件 2. 基于XML注解方式声明bean 自定义bean 第三方bean 3.注解方式声明配置类 扩展1,FactoryBean 扩展2,加载配置类并加载配置文件(系统迁移) 扩展3,proxyBeanMethodstrue的使用 4. 使用Import注解导入要注入的bean…...
《吐血整理》进阶系列教程-拿捏Fiddler抓包教程(13)-Fiddler请求和响应断点调试
1.简介 Fiddler有个强大的功能,可以修改发送到服务器的数据包,但是修改前需要拦截,即设置断点。设置断点后,开始拦截接下来所有网页,直到取消断点。这个功能可以在数据包发送之前,修改请求参数;…...
Android 13(T) - Media框架(1)- 总览
从事Android Media开发工作三年有余,刚从萌新变成菜鸟,一路上跌跌撞撞学习,看了很多零零碎碎的知识,为了加深对Android Media框架的理解,决定在这里记录下学习过程中想到的一些问题以及一些思考,也希望对初…...
+antdesignvue项目框架搭建基本步骤)
简述vue3(ts)+antdesignvue项目框架搭建基本步骤
目录 项目简介 概念 过程简述 基本步骤 1.创建新项目 2.安装Ant Design Vue 3.配置Ant Design Vue 4.创建页面和组件 5.使用组件 6.运行项目 项目简介 概念 Vue 3(使用TypeScript)和Ant Design Vue项目框架搭建是指在Vue 3框架下,…...

webpack : 无法加载文件 C:\Program Files\nodejs\webpack.ps1
webpack : 无法加载文件 C:\Program Files\nodejs\webpack.ps1 1.问题2. 解决办法: 1.问题 使用webpack打包是报错如下: webpack : 无法加载文件 C:\Program Files\nodejs\webpack.ps1,因为在此系统上禁止运行脚本。有关详细信息,…...
OGRLayer篇 代码示例)
GDAL OGR C++ API 学习之路 (5)OGRLayer篇 代码示例
GetStyleTable virtual OGRStyleTable *GetStyleTable () 返回图层样式表 返回: 指向不应由调用方修改或释放的样式表的指针 // 假设图层对象为 poLayer OGRStyleTable* poStyleTable poLayer->GetStyleTable(); if (poStyleTable ! nullptr) {// 处理样式表信息// ..…...

NIDEC COMPONENTS尼得科科宝滑动型DIP开关各系列介绍
今天AMEYA360对尼得科科宝电子滑动型DIP开关各系列参数进行详细介绍,方便大家选择适合自己的型号。 系列一、滑动型DIP开关 CVS 针脚数:1, 2, 3, 4, 8 安装类型:表面贴装,通孔 可水洗:无 端子类型:PC引脚(只…...
一起学算法(滑动窗口篇)
前言: 对于滑动窗口,有长度固定的窗口,也有长度可变的窗口,一般是基于数组进行求解,对于一个数组中两个相邻的窗口,势必会有一大部分重叠,这部分重叠的内容是不需要重复计算的,所以我…...

HTML <q> 标签
实例 标记短的引用: <q>Here is a short quotation here is a short quotation</q>浏览器支持 元素ChromeIEFirefoxSafariOpera<q>YesYesYesYesYes所有浏览器都支持 <q> 标签。 定义和用法 <q> 标签定义短的引用。 浏览器经常在引用的内容…...

机器学习02-再识K邻近算法(自定义数据集训练及测试)
定义: 如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。简单的说就是根据你的“邻居”来推断出你的类别。 用个成语就是物以类聚 思想: 如果一个样本在特征空间中的K个最…...

github使用笔记及git协作常用命令
1.Github有一个主库,每个人自己也有一个库,称为分支。 2.Github的协作流程:先从主库fork出自己的分支, 然后进行代码的修改等操作, 操作完之后从本地库上推到自己的服务器分支,然后 服务器分支Pull Request到 主库。 3.本地仓库由git维护的三棵“树"组成:第1个…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...
