分治法 Divide and Conquer
1.分治法
分治法(Divide and Conquer)是一种常见的算法设计思想,它将一个大问题分解成若干个子问题,递归地解决每个子问题,最后将子问题的解合并起来得到整个问题的解。分治法通常包含三个步骤:
- 1. Divide:将问题分解成若干个子问题。
- 2. Conquer:递归地解决每个子问题。
- 3. Combine:将子问题的解合并起来得到整个问题的解。
分治法的主要思想是将问题分解成若干个相互独立的子问题,通过递归地解决每个子问题,最后将子问题的解合并起来得到整个问题的解。这种思想可以应用于许多问题的解法中,如排序、搜索、图论、数学计算等等。
一些常见的使用分治法的算法包括:归并排序、快速排序、二分搜索、线性时间选择、Karatsuba 算法等等。
2.练习题
1)
力扣![]() https://leetcode.cn/problems/different-ways-to-add-parentheses/解题思路:
https://leetcode.cn/problems/different-ways-to-add-parentheses/解题思路:
依次遍历字符串的每个字符,如果是运算符,就递归计算左边和右边的值。
class Solution {
public:vector<int> diffWaysToCompute(string expression) {int n = expression.size();vector<int> res;for(int i=0;i<n;i++){char c = expression[i];if(c=='+'||c=='-'||c=='*'){vector<int> left = diffWaysToCompute(expression.substr(0,i));vector<int> right = diffWaysToCompute(expression.substr(i+1));for(auto l:left){for(auto r:right){switch(c){case '+': res.push_back(l+r);break;case '-': res.push_back(l-r);break;case '*': res.push_back(l*r);break;}}}}}if(res.empty()) res.push_back(stoi(expression));return res;}};2)
力扣![]() https://leetcode.cn/problems/beautiful-array/description/
https://leetcode.cn/problems/beautiful-array/description/
解题思路:
首先确定一点,怎么满足这个条件:
- 对于每个
0 <= i < j < n,均不存在下标k(i < k < j)使得2 * nums[k] == nums[i] + nums[j]。
最简单的方法就是让右边的nums[i] + nums[j] 这个表达式的值为奇数,因为2 * nums[k]肯定是偶数。这样我们可以假设i<j,且nums[i]为奇数,nums[j]为偶数。也就是让数组左边为奇数,右边为偶数。
又因为如果A是漂亮数组,那么a*A+b还是漂亮数组。
所有我们可以用分治法,将问题从大到小拆解,先满足每个长度为1、2、3......的数组都是漂亮数组,这样最后长度为n的数组也是漂亮数组。
代码:
class Solution {
public:vector<int> beautifulArray(int n) {vector<int> res(n,1);part(0,n-1,res);return res;}void part(int left, int right, vector<int>& res){if(left>=right) return;int mid = left + (right-left)/2;part(left, mid, res);part(mid+1, right, res);for(int i=left;i<=mid;i++){res[i] = 2*res[i]-1;}for(int i=mid+1;i<=right;i++){res[i] = 2*res[i];}}
};相关文章:
分治法 Divide and Conquer
1.分治法 分治法(Divide and Conquer)是一种常见的算法设计思想,它将一个大问题分解成若干个子问题,递归地解决每个子问题,最后将子问题的解合并起来得到整个问题的解。分治法通常包含三个步骤: 1. Divid…...
.__init__()的作用是什么?)
super(Module_ModuleList, self).__init__()的作用是什么?
class Module_ModuleList(nn.Module):def __init__(self):super(Module_ModuleList, self).__init__()self.linears nn.ModuleList([nn.Linear(10, 10)])在这段代码中,super(Module_ModuleList, self).__init__() 的作用是调用父类 nn.Module 的 __init__ 方法&…...
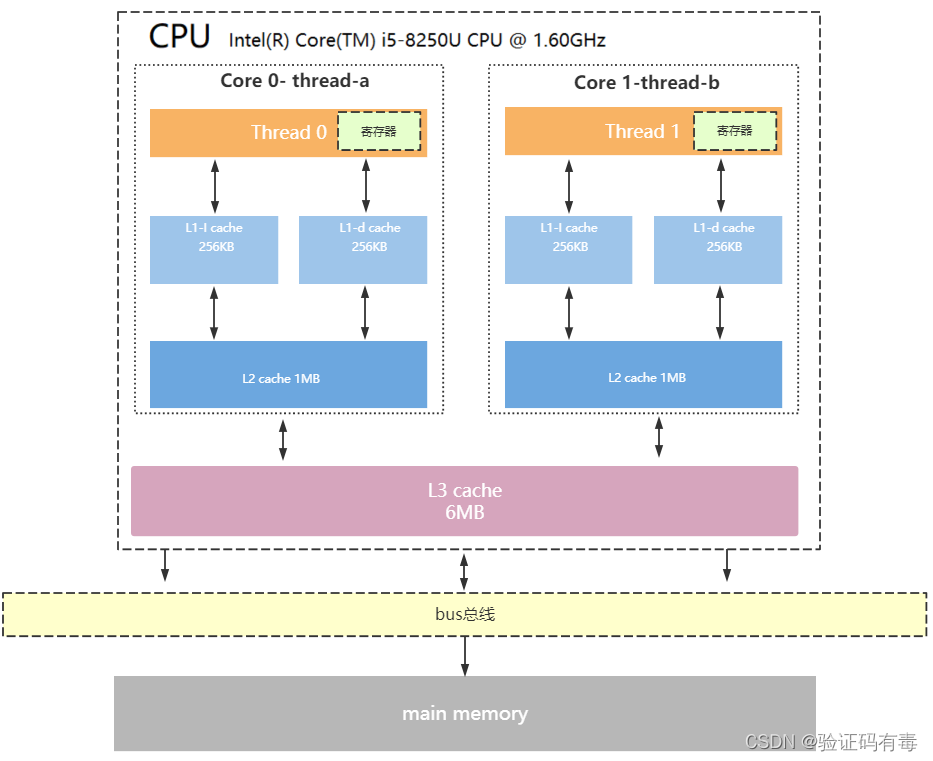
【并发专题】操作系统模型及三级缓存架构
目录 课程内容一、冯诺依曼计算机模型详解1.计算机五大核心组成部分2.CPU内部结构3.CPU缓存结构4.CPU读取存储器数据过程5.CPU为何要有高速缓存 学习总结 课程内容 一、冯诺依曼计算机模型详解 现代计算机模型是基于-冯诺依曼计算机模型 计算机在运行时,先从内存中…...
)
java基础复习(第二日)
java基础复习(二) 1.抽象的(abstract)方法是否可同时是静态的(static),是否可同时是本地方法(native),是否可同时被 synchronized修饰? 都不能。 抽象方法需要子类重写…...
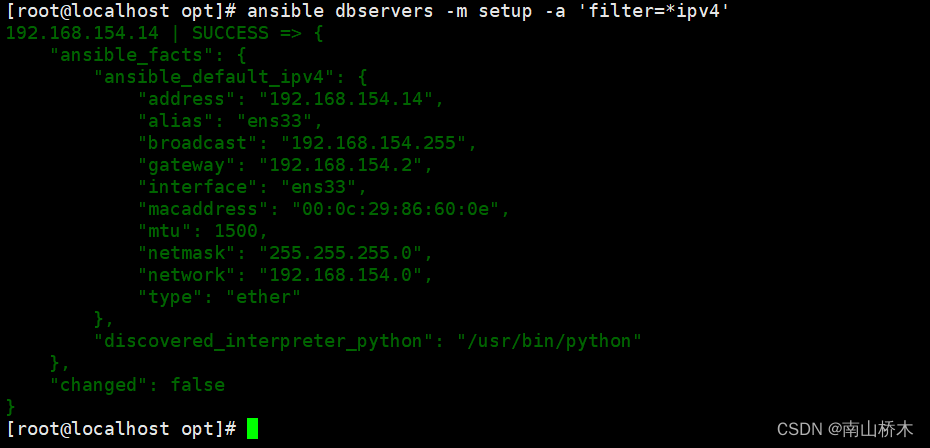
Ansible自动化运维工具
Ansible自动化运维工具 一、ansible介绍二、ansible环境安装部署三、ansible命令行模块1、command模块2、shell模块3、cron模块4、user模块5、group模块6、copy模块7、file模块8、hostname模块9、ping模块10、yum模块11、service/systemd模块12、script模块13、mount模块14、ar…...
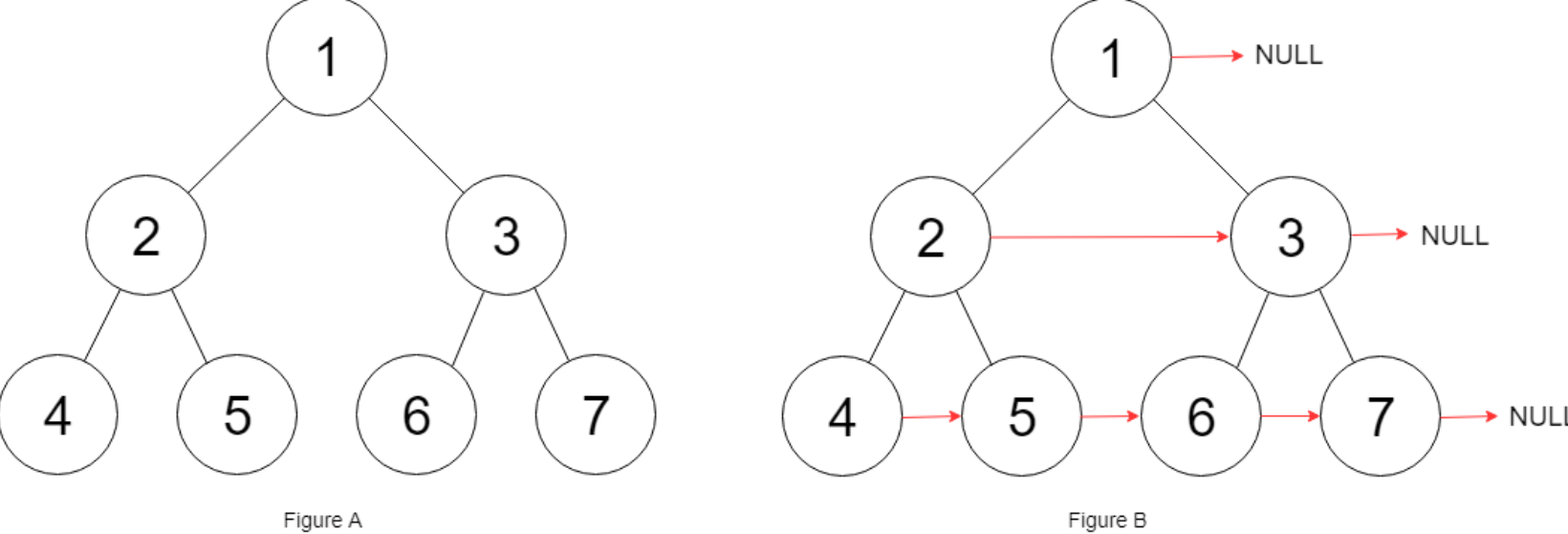
LeetCode-116-填充每个节点的下一个右侧节点指针
一:题目描述: 给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下: struct Node {int val;Node *left;Node *right;Node *next; }填充它的每个 next 指针,让这个指…...
每篇10题)
前端面试的性能优化部分(3)每篇10题
21.如何优化移动端网页的性能? 优化移动端网页的性能是提升用户体验、降低用户流失的关键。以下是一些优化移动端网页性能的常见方法: 压缩和合并资源: 压缩 CSS、JavaScript 和图片等静态资源,减少文件大小,同时合并…...

如何通过企业工商信息初步判断企业是否靠谱?
银行、投资机构等对企业进行融资、授信、合作时,需要如何评估企业的可靠性。企业工商信息作为企业的基础信息,是初步判断企业是否靠谱的重要依据之一,通过对企业工商信息的综合分析,我们可以了解企业的经营状况、财务实力、法律风…...

ChatGPT+知乎,20分钟超越专业大V的调教方法
AI技术正在迅速发展,渗透到我们的生活中,尤其在内容营销领域。 AI算法帮助我们生成文本、优化搜索引擎排名,提升用户体验等,这些创新正在塑造时代的前进方向,AI也将引领未来十年的变革。对于每个创业者、内容创作者和…...

git branch --show-current 和 git rev-parse --abbrev-ref HEAD 区别
git branch --show-current 和 git rev-parse --abbrev-ref HEAD 区别 git branch --show-current 和 git rev-parse --abbrev-ref HEAD 命令都可以用于获取当前所在的 Git 分支名称。 但是,它们之间有一些不同点: git branch --show-current 命令是 G…...
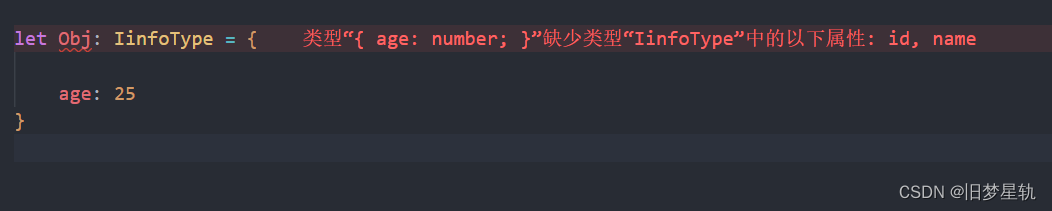
【TypeScript】接口类型 Interfaces 的使用理解
导语: 什么是 类型接口? 在面向对象语言中,接口(Interfaces)是一个很重要的概念,它是对行为的抽象,而具体如何行动需要由类(classes)去实现(implement&#x…...
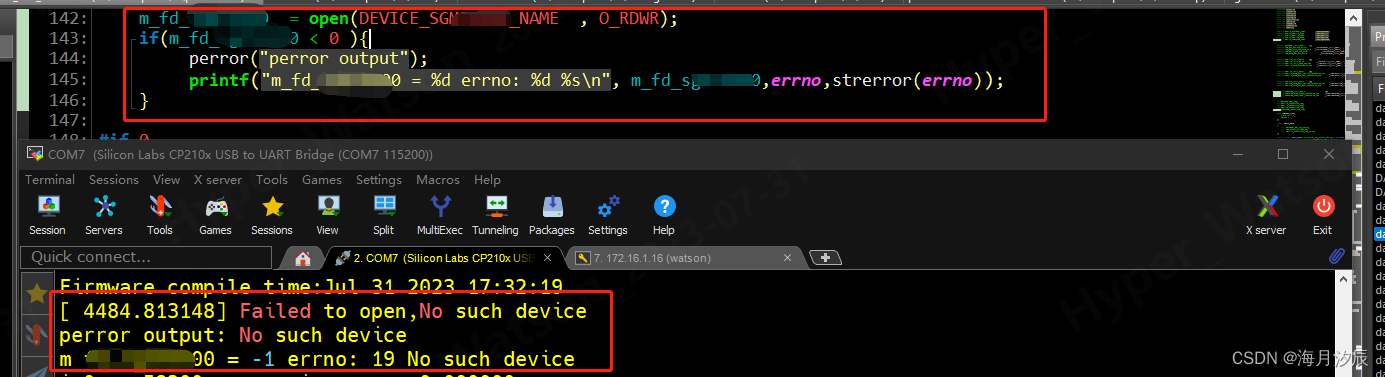
2023-07-31 C语言根据错误号打印详细的错误信息perror(““) 或者strerror(errno)
一、C 语言可以使用perror("perror output"); 或 strerror(errno)打印详细的错误信息。 二、需要的头文件#include <errno.h>。 三、实例测试,这里我让open一个linux 底层杂项设备失败的情况,返回的是一个负数,强制返回-EN…...
JDK17和JDK8完美卸载方法及新版JDK安装教程
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...
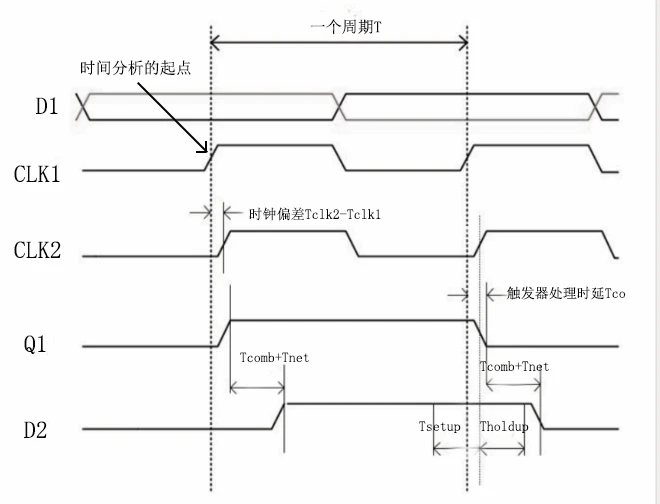
FPGA设计时序分析二、建立/恢复时间
目录 一、背景知识 1.1 理想时序模型 1.2 实际时序模型 1.2.1 时钟不确定性 1.2.2 触发器特性 二、时序分析 2.1 时序模型图 2.2 时序定性分析 一、背景知识 之前的章节提到,时钟对于FPGA的重要性不亚于心脏对于人的重要性,所有的逻辑运算都离开…...

oracle建立自动增长字段
oracle数据库与其他的数据库不太一样,比如在mysql里自动增长只要设定“auto_increment”即可。可是在oracle里就没有这种配置了。以oracle11g为例,建立自动增长的字段。操作如下: --创建表 create table USERINFO ( ID NUMBER , …...
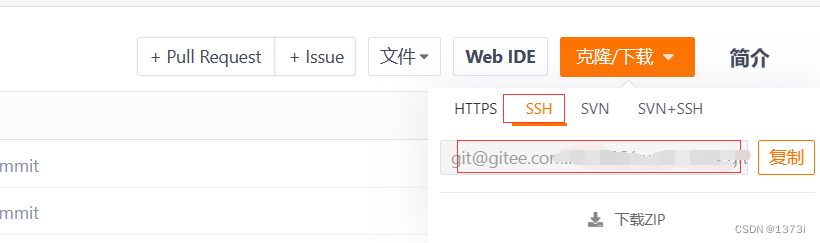
【Git】远程仓库的创建、SSH协议克隆、拉取、推送
目录 一、创建远程仓库 二、HTTPS协议克隆仓库 三、SSH协议克隆仓库 四、向远程仓库推送 五、从远程仓库拉取 六、忽略特殊文件 七、配置命令别名 一、创建远程仓库 首先我们可以从GitHub或者Gitee中创建自己的个人仓库 工作台 - Gitee.comhttps://gitee.com/ 二、HTT…...

C#之泛型
目录 一、概述 二、C#中的泛型 继续栈的示例 三、泛型类 (一)声明泛型类 (二)创建构造类型 (三)创建变量和实例 (四)比较泛型和非泛型栈 四、类型参数的约束 (一…...
Scrum敏捷开发管理流程+scrum工具免费
Leangoo领歌它覆盖了敏捷项目研发全流程,包括小型团队Scrum敏捷开发,规模化敏捷SAFe,Scrum of Scrums大规模敏捷。它提供了灵活的敏捷模板和极致的协作体验,可以让团队快速上手,快速落地Scrum敏捷开发管理。 首先建立产…...

【操作系统基础】Linux 中 /var/log/ 文件夹下通常有哪一些文件?分别的作用是什么?
在Linux系统中,/var/log/ 文件夹通常包含了系统日志文件,这些文件记录了系统的各种活动和事件,以便管理员进行故障排除和监控。 以下是/var/log/ 文件夹中常见的一些文件及其含义: auth.log:记录系统认证和授权相关的…...

【构造】CF1758 C
Problem - 1758C - Codeforces 题意: 思路: 思路: #include <bits/stdc.h>#define int long longusing namespace std;const int mxn2e510; const int mxe2e510;int N,x; int ans[mxn];void solve(){cin>>N>>x;if(N%x!0)…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
)
2025.6.9总结(利与弊)
凡事都有两面性。在大厂上班也不例外。今天找开发定位问题,从一个接口人不断溯源到另一个 接口人。有时候,不知道是谁的责任填。将工作内容分的很细,每个人负责其中的一小块。我清楚的意识到,自己就是个可以随时替换的螺丝钉&…...

表单设计器拖拽对象时添加属性
背景:因为项目需要。自写设计器。遇到的坑在此记录 使用的拖拽组件时vuedraggable。下面放上局部示例截图。 坑1。draggable标签在拖拽时可以获取到被拖拽的对象属性定义 要使用 :clone, 而不是clone。我想应该是因为draggable标签比较特。另外在使用**:clone时要将…...
