数字图像处理(番外)图像增强
图像增强
图像增强的方法是通过一定手段对原图像附加一些信息或变换数据,有选择地突出图像中感兴趣的特征或者抑制(掩盖)图像中某些不需要的特征,使图像与视觉响应特性相匹配。
图像对比度
图像对比度计算方式如下:
C = ∑ δ δ ( i , j ) P δ ( i , j ) C=\displaystyle\sum_{{\delta}}\delta(i,j)P_\delta(i,j) C=δ∑δ(i,j)Pδ(i,j)
其中, δ ( i , j ) = ∣ i − j ∣ \delta(i,j)=\lvert i-j\rvert δ(i,j)=∣i−j∣,即相邻像素间的灰度差; P δ ( i , j ) P_\delta(i,j) Pδ(i,j)为相邻像素灰度差为 δ \delta δ的像素分布概率。可以是四邻域,也可以是八邻域。具体过程如下:
原始图像为:
L = [ 1 3 5 2 1 3 3 6 0 ] L=\begin{bmatrix} 1 & 3 &5\\ 2 & 1 &3 \\ 3 & 6&0 \end{bmatrix} L= 123316530
按照四邻域进行计算,对比度 C L = [ ( 1 2 + 2 2 ) + ( 2 2 + 2 2 + 2 2 ) + ( 1 2 + 1 2 + 1 2 ) + ( 2 2 + 2 2 + 1 2 + 5 2 ) + ( 2 2 + 2 2 + 3 2 ) + ( 1 2 + 3 2 ) + ( 5 2 + 3 2 + 6 2 ) + ( 3 2 + 6 2 ) / 22 C_L=\lbrack(1^2+2^2)+(2^2+2^2+2^2)+(1^2+1^2+1^2)+(2^2+2^2+1^2+5^2)+(2^2+2^2+3^2)+(1^2+3^2)+(5^2+3^2+6^2)+(3^2+6^2)/22 CL=[(12+22)+(22+22+22)+(12+12+12)+(22+22+12+52)+(22+22+32)+(12+32)+(52+32+62)+(32+62)/22。22就是平方的个数。
1.对比度展宽
对比度展宽的目的是通过增强图像的亮暗对比程度而改善画质,使图像的显示效果更加清晰。
线性对比度展宽
通过抑制非重要信息的对比度来腾出空间给重要信息进行对比度的展宽。
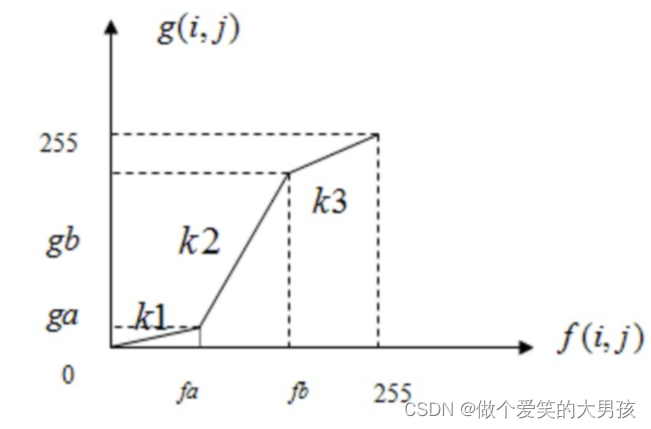
原图的灰度为 f ( i , j ) f(i,j) f(i,j),处理后的图像灰度为 g ( i , j ) g(i,j) g(i,j)。原图中的重要景物的灰度分布假设分布在 [ f a , f b ] \lbrack f_a,f_b\rbrack [fa,fb]的范围内,则对比度线性展宽的目的是使处理后图像的重要景物的灰度分布在 [ g a , g b ] \lbrack g_a,g_b\rbrack [ga,gb]的范围内,当 Δ f = ( f b − f a ) < Δ g = ( g b − g a ) \varDelta f=(f_b-f_a)<\varDelta g=(g_b-g_a) Δf=(fb−fa)<Δg=(gb−ga),则可达到对比度展宽的目的。
计算方式如下:
g ( i , j ) = { α f ( i , j ) 0 ≤ f ( i , j ) < a β ( f ( i , j ) − a ) + g a a ≤ f ( i , j ) < b γ ( f ( i , j ) − b ) + g b b ≤ f ( i , j ) < 255 g(i,j)= \begin{cases} \alpha f(i,j) &\text{ } 0\le f(i,j)<a \\ \beta (f(i,j)-a)+g_a &\text{ } a\le f(i,j)<b \\ \gamma (f(i,j)-b)+g_b &b\le f(i,j)<255 \end{cases} g(i,j)=⎩ ⎨ ⎧αf(i,j)β(f(i,j)−a)+gaγ(f(i,j)−b)+gb 0≤f(i,j)<a a≤f(i,j)<bb≤f(i,j)<255
其中, α = g a f a , β = g b − g a f b − f a , γ = 255 − g b 255 − f b \alpha =\frac{g_a}{f_a},\beta =\frac{g_b-g_a}{f_b-f_a},\gamma =\frac{255-g_b}{255-f_b} α=faga,β=fb−fagb−ga,γ=255−fb255−gb。
C++代码如下:
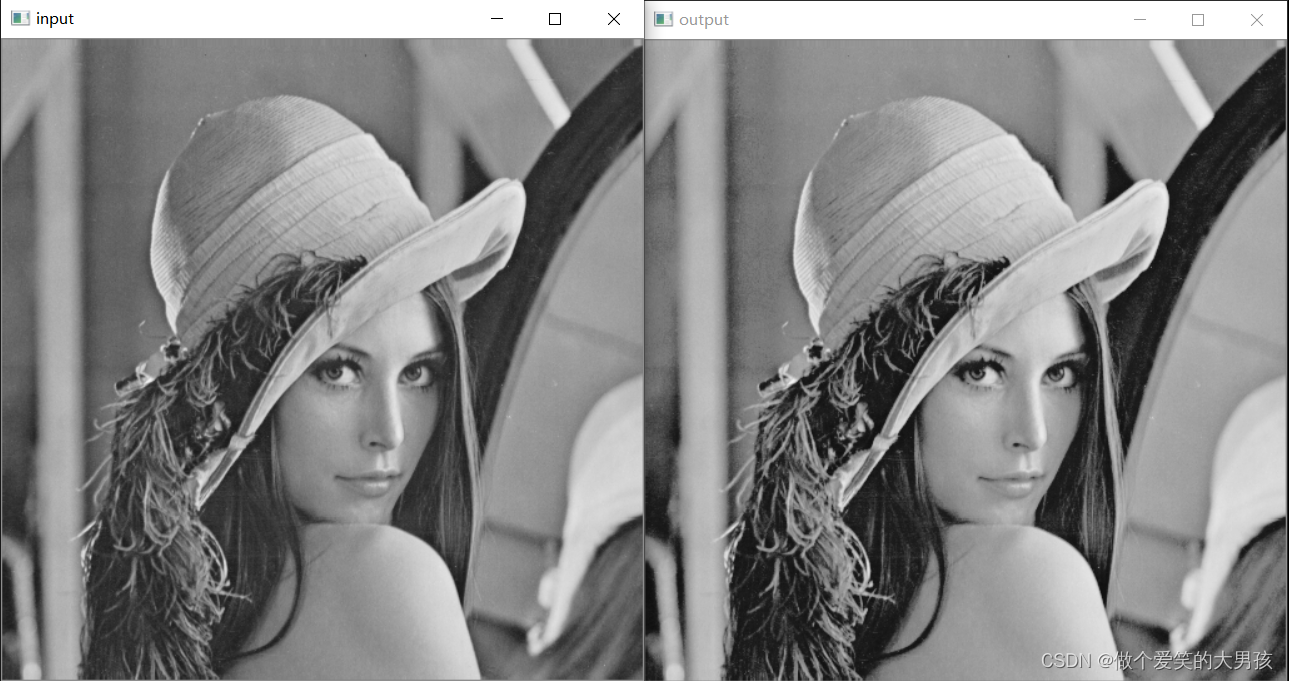
cv::Mat image = cv::imread("Lena.bmp");cv::Mat grayImage(image.size(), CV_8UC1);cv::Mat dstImage(grayImage.size(), CV_8UC1);cv::cvtColor(image, grayImage, CV_BGR2GRAY);int fa = 50, fb = 100;float ga = 30, gb = 120;for (int row = 0; row < grayImage.rows; row++){uchar *currentData = grayImage.ptr<uchar>(row);for (int col = 0; col < grayImage.cols; col++){if (*(currentData + col) >= 0 && *(currentData + col) < fa){dstImage.at<uchar>(row, col) = uchar(ga / fa * (*(currentData + col)));}if (*(currentData + col) >= fa && *(currentData + col) < fb){dstImage.at<uchar>(row, col) = uchar((gb-ga) / (fb-fa) * (*(currentData + col)-fa)+ga);}if (*(currentData + col) >= fb && *(currentData + col) < 255){dstImage.at<uchar>(row, col) = uchar((255-gb) / (255-fb) * (*(currentData + col)-fb)+gb);}}//currentData++;}
结果如下:
非线性对比度展宽
通过一个光滑的映射曲线,使得处理后图像的灰度变化比较光滑。计算公式如下:
g ( i , j ) = c ⋅ l g ( 1 + f ( i , j ) ) g(i,j)=c\cdot lg(1+f(i,j)) g(i,j)=c⋅lg(1+f(i,j))
实际上完成的作用是,抑制高亮度区域,扩展低亮度区域。
2.直方图均衡化
在信息论中有这样一个结论:当数据的分布接近均匀分布的时候,数据所承载的信息量(熵)为最大。
灰度直方图的基本原理是:对在图像中像素个数多的灰度级(即对画面起主要作用的灰度值)进行展宽,而对像素个数少的灰度值(即对画面不起主要作用的灰度值)进行归并。
直方图均衡化方法的具体步骤如下:
- 求出原图 f ( i , j ) M × N f(i,j)_{M\times N} f(i,j)M×N的灰度直方图,设用256维的向量 h f h_f hf表示;
- 有 h f h_f hf求原图的灰度分布概率,记作 p f p_f pf,则有 p f ( i ) = 1 N f ⋅ h f ( i ) , i = 0 , 1 , … , 255 p_f(i)=\frac{1}{N_f}\cdot h_f(i),i=0,1,\dots ,255 pf(i)=Nf1⋅hf(i),i=0,1,…,255
其中, N f = M × N N_f=M\times N Nf=M×N( M , N M,N M,N分别为图像的长和宽)为图像的总像素个数; - 计算图像各个灰度值的累计分布概率,记作 p a p_a pa,则有 p a ( i ) = ∑ k = 0 i p f ( k ) , i = 1 , 2 , … , 255 p_a(i)=\displaystyle\sum_{k=0}^ip_f(k),i=1,2,\dots ,255 pa(i)=k=0∑ipf(k),i=1,2,…,255
其中,令 p a ( 0 ) = 0 p_a(0)=0 pa(0)=0。 - 进行直方图均衡化计算,得到处理后图像的像素值 g ( i , j ) g(i,j) g(i,j)为: g ( i , j ) = 255 ⋅ p a ( k ) g(i,j)=255\cdot p_a(k) g(i,j)=255⋅pa(k)
C++代码如下所示:
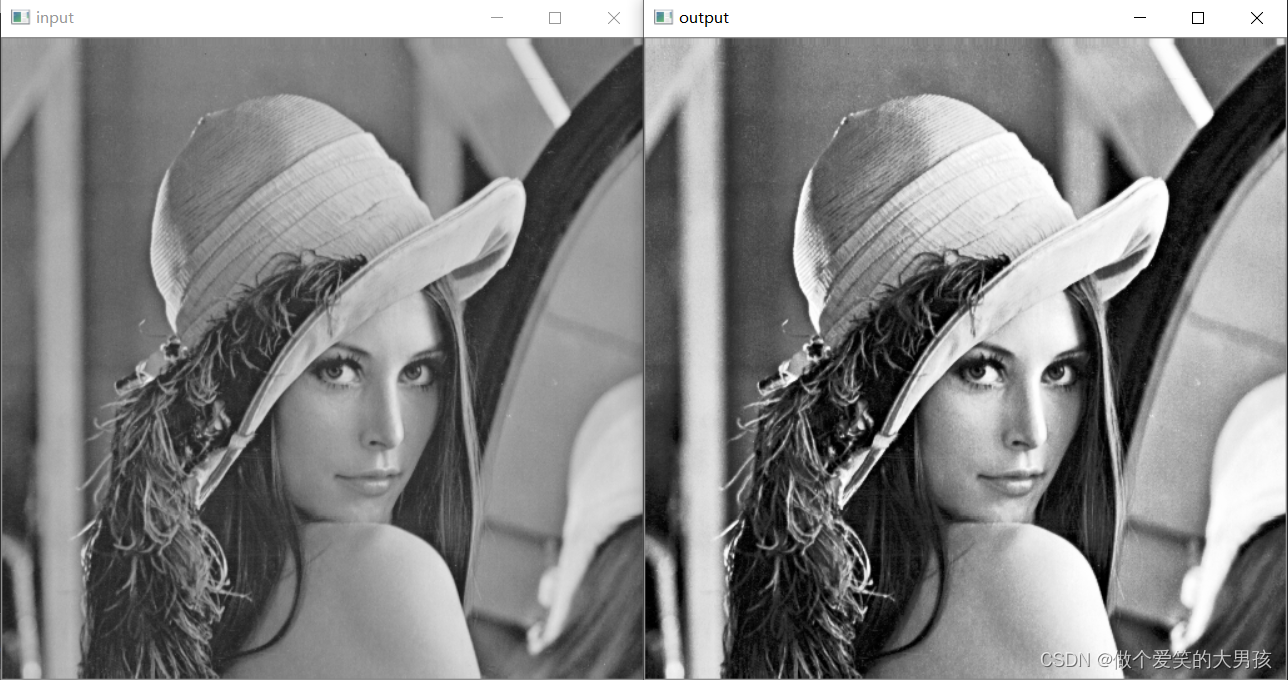
cv::Mat image = cv::imread("Lena.bmp");cv::Mat src(image.size(), CV_8UC1);//转为灰度图像cv::cvtColor(image, src, CV_BGR2GRAY);cv::Mat dst(image.size(), CV_8UC1);float hf[256] = { 0 };for (int row = 0; row < src.rows; row++){uchar *currentData = src.ptr<uchar>(row);for (int col = 0; col < src.cols; col++){hf[*(currentData + col)] += 1;}}float pf[256] = { 0 };for (int i = 0; i < 256; i++){pf[i] = hf[i] / (src.rows*src.cols);}float pa[256] = { 0 };for (int i = 1; i < 256; i++){float sumNumber = 0;for (int j = 0; j < i+1; j++){sumNumber += pf[j];}pa[i] = sumNumber;}for (int row = 0; row < dst.rows; row++){uchar * currentData = dst.ptr<uchar>(row);for (int col = 0; col < dst.cols; col++){*(currentData + col) = uchar(255 * pa[src.at<uchar>(row, col)]);}}
结果展示:
相关文章:

数字图像处理(番外)图像增强
图像增强 图像增强的方法是通过一定手段对原图像附加一些信息或变换数据,有选择地突出图像中感兴趣的特征或者抑制(掩盖)图像中某些不需要的特征,使图像与视觉响应特性相匹配。 图像对比度 图像对比度计算方式如下: C ∑ δ δ ( i , j …...

flutter:轮播
前言 介绍几个比较有不错的轮播库 swipe_deck 与轮播沾边,但是更多的是一种卡片式的交互式界面设计。它的主要概念是用户可以通过左右滑动手势浏览不同的卡片,每张卡片上都有不同的信息或功能。 Swipe deck通常用于展示图片、产品信息、新闻文章、社…...

高忆管理:股票投资策略是什么?有哪些?
在进行股票买卖过程中,出资者需求有自己的方案和出资战略,并且主张严格遵从出资战略买卖,不要跟风操作。那么股票出资战略是什么?有哪些?下面就由高忆管理为我们剖析: 股票出资战略简略来说便是能够协助出资…...
为公网SSH远程Ubuntu配置固定的公网TCP端口地址主图
文章目录 为公网SSH远程Ubuntu配置固定的公网TCP端口地址 为公网SSH远程Ubuntu配置固定的公网TCP端口地址 在上篇文章中,我们通过cpolar建立的临时TCP数据隧道,成功连接了位于其他局域网下的Ubuntu系统,实现了不同操作系统、不同网络下的系统…...

【前端知识】React 基础巩固(四十一)——手动路由跳转、参数传递及路由配置
React 基础巩固(四十一)——手动路由跳转、参数传递及路由配置 一、实现手动跳转路由 利用 useNavigate 封装一个 withRouter(hoc/with_router.js) import { useNavigate } from "react-router-dom"; // 封装一个高阶组件 function withRou…...

Qt几种字符类型的相互转换
Qt几种字符类型的相互转换 将const QString转换为const char*将const char*转换为const QStringQstring转换为string把string转换为QstringQt中弹出一个窗口 将const QString转换为const char* #include <QString> #include <iostream>int main() {const QString …...

软件测试员的非技术必备技能
成为软件测试人员所需的技能 非技术技能 以下技能对于成为优秀的软件测试人员至关重要。 将您的技能组合与以下清单进行比较,以确定软件测试是否适合您 - 分析技能:优秀的软件测试人员应具备敏锐的分析能力。 分析技能将有助于将复杂的软件系统分解为…...

渗透测试:Linux提权精讲(二)之sudo方法第二期
目录 写在开头 sudo expect sudo fail2ban sudo find sudo flock sudo ftp sudo gcc sudo gdb sudo git sudo gzip/gunzip sudo iftop sudo hping3 sudo java 总结与思考 写在开头 本文在上一篇博客的基础上继续讲解渗透测试的sudo提权方法。相关内容的介绍与背…...
ansible安装lnmp(集中式)
文章目录 一、安装nginx二、安装mysql三、安装php测试: 一、安装nginx - name: the nginx playhosts: webserversremote_user: roottasks:- name: stop firewalld #关闭防火墙service: namefirewalld statestopped enabledno- name: selinux stopc…...

Tomcat的基本使用,如何用Maven创建Web项目、开发完成部署的Web项目
Tomcat 一、Tomcat简介二、Tomcat基本使用三、Maven创建Web项目3.1 Web项目结构3.2开发完成部署的Web项目3.3创建Maven Web项目3.3.1方式一3.3.2方式二(个人推荐) 总结 一、Tomcat简介 Web服务器: Web服务器是一个应用程序(软件&…...

微信小程序测试要点
一、什么是小程序? 可以将小程序理解为轻便的APP,不用安装就可以使用的应用。用户通过扫一扫或者搜索的方式,就可以打开应用。 小程序最主要的特点是内嵌于微信之中,而使用小程序的目的是为了能够方便用户不在受下载多个APP的烦…...
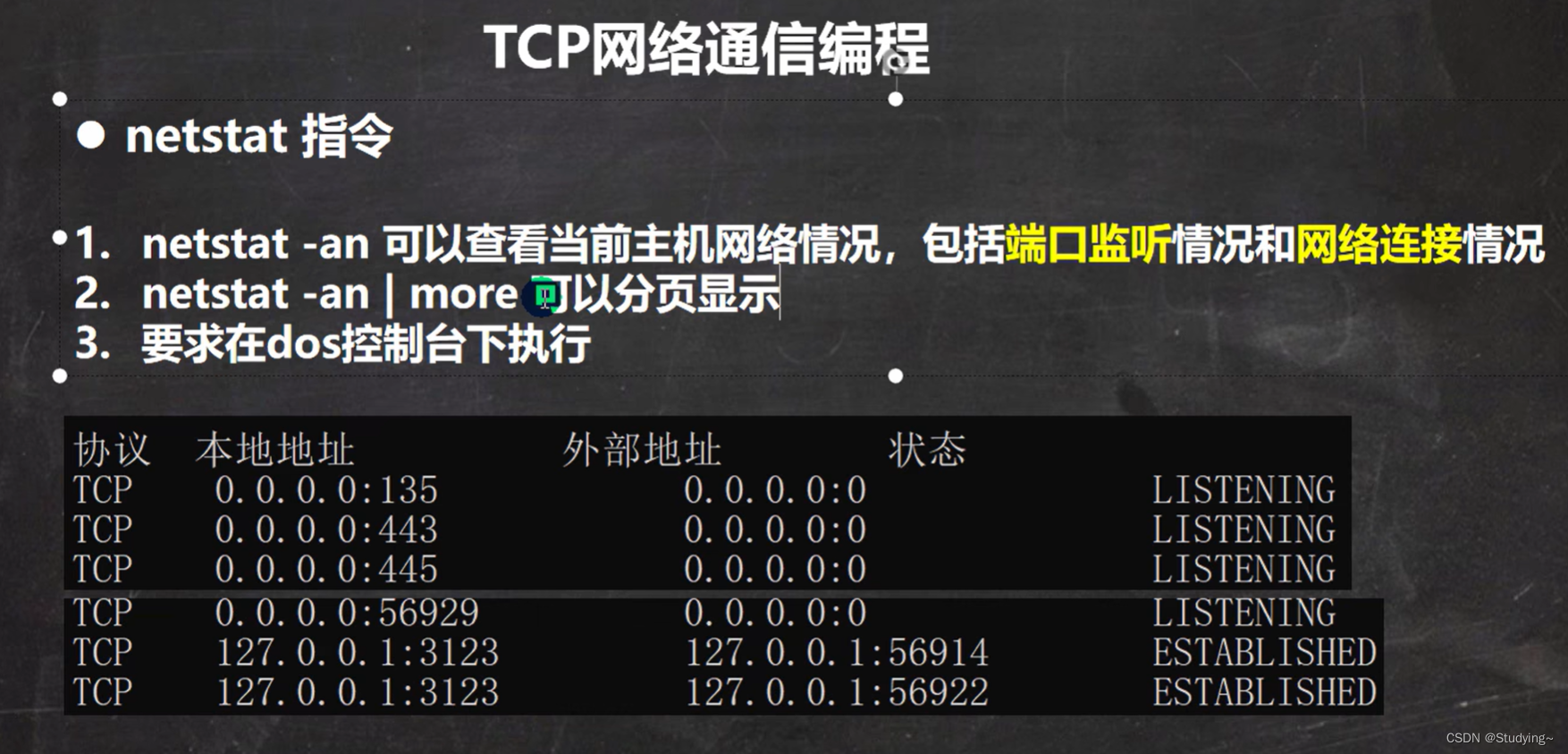
TCP网络通信编程之netstat
【netstat指令】 【说明】 (1)Listening 表示某个端口在监听 (2)如果有一个外部程序(客户端)连接到该端口,就会显示一条连接信息 (3)指令netstat -anb 可以参看是那个…...

Stable Diffusion:网页版 体验 / AI 绘图
一、官网地址 Stable Diffusion Online 二、Stable Diffusion AI 能做什么 Stable Diffusion AI绘图是一种基于Stable Diffusion模型的生成式AI技术,能够生成各种类型的图像,包括数字艺术、照片增强和图像修复等。以下是一些可能的应用: …...

一文了解JavaScript 与 TypeScript的区别
TypeScript 和 JavaScript 是两种互补的技术,共同推动前端和后端开发。在本文中,我们将带您快速了解JavaScript 与 TypeScript的区别。 一、TypeScript 和 JavaScript 之间的区别 JavaScript 和 TypeScript 看起来非常相似,但有一个重要的区…...

从更广阔的角度看待产业互联网,它展现的是一次重构的过程
如果产业互联网仅仅只是在传统的供求关系之下,如果产业互联网仅仅只是在传统的平衡之下,缺少了一次对于供求关系的重新建构,那么,所谓的产业互联网,依然是无法跳出以往的发展困境,依然是无法摆脱以往的发展…...

【PHP】简记问题:使用strtotime(‘-1 month‘, time)获取上个月第一天时间戳出错
发生场景 在7月31号是查看统计上个月订单购买总金额,查询结果为0 $preMonthStart strtotime(date(Ym01, strtotime("-1 month"))); $curMonthStart strtotime(date(Ym01)); # 统计上月份实际订单金额 $sql "SELECT count(money) FROM orders WH…...
舌体分割的初步展示应用——依托Streamlit搭建demo
1 前言 去年在社区发布了有关中医舌象诊断的博文,其中舌象识别板块受到了极高的关注和关注。😊最近,我接触到了Python的Streamlit库,它可以帮助数据相关从业人员轻松搭建数据看板。本文将介绍如何使用Streamlit构建舌体分割的演示…...

从Vue层面 - 解析发布订阅模式和观察者模式区别
目录 前言一、发布订阅模式什么是发布订阅模式?应用场景 二、观察者模式1)什么是观察者模式?2)应用场景3)vue中的观察者模式观察者(订阅者) - Watcher目标者(发布者) - D…...
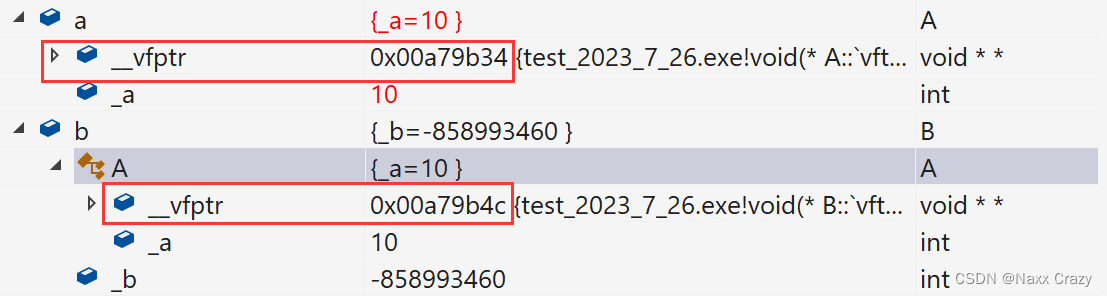
面向对象之_多态_1
目录 一. 多态 多态是什么 二. 多态的构成条件 1. 虚函数 2. 虚函数重写(隐藏) 3. 父类型的引用或者指针调用 4. 多态的特殊情况 1) 子类可以不加 virtual 关键字 2) 协变 三. 关键字 1. virtual 2. final 3. override 四. 多态的原理 1. 虚…...
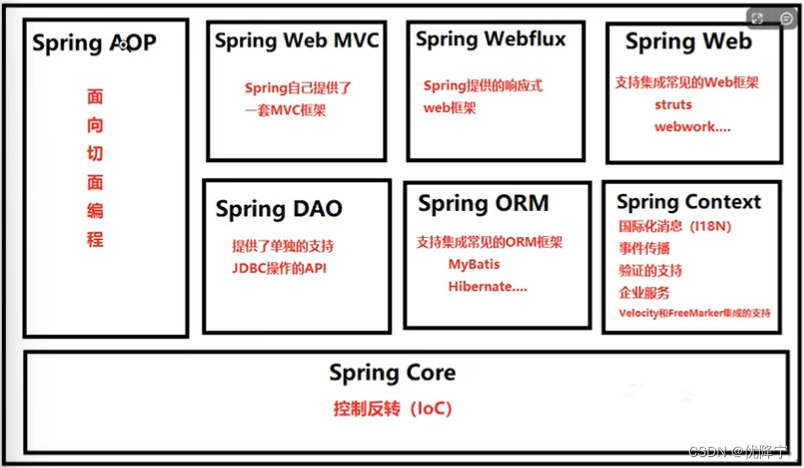
Spring学习笔记之spring概述
文章目录 Spring介绍Spring8大模块Spring特点 Spring介绍 Spring是一个轻量级的控制反转和面向切面的容器框架 Spring最初的出现是为了解决EJB臃肿的设计,以及难以测试等问题。 Spring为了简化开发而生,让程序员只需关注核心业务的实现,尽…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
react更新页面数据,操作页面,双向数据绑定
// 路由不是组件的直接跳转use client,useEffect,useRouter,需3个结合, use client表示客户端 use client; import { Button,Card, Space,Tag,Table,message,Input } from antd; import { useEffect,useState } from react; impor…...

break 语句和 continue 语句
break语句和continue语句都具有跳转作用,可以让代码不按既有的顺序执行 break break语句用于跳出代码块或循环 1 2 3 4 5 6 for (var i 0; i < 5; i) { if (i 3){ break; } console.log(i); } continue continue语句用于立即终…...

【基于阿里云搭建数据仓库(离线)】使用UDTF时出现报错“FlatEventUDTF cannot be resolved”
目录 问题: 可能的原因有: 解决方法: 问题: 已经将包含第三方依赖的jar包上传到dataworks,并且成功注册函数,但是还是报错:“FlatEventUDTF cannot be resolved”,如下:…...
