计算机图形学笔记2-Viewing 观测
观测主要解决的问题是如何把物体的三维“模型”变成我们在屏幕所看到的二维“图片”,我们在计算机看到实体模型可以分成这样几步:

- 相机变换(camera transformation)或眼变换(eye transformation):想象把相机放在任意一个位置来观测物体,我们首先就要把物体的世界坐标转换为相机坐标,这一步称为相机变换或眼变换。
- 投影变换(projection transformation):相机把物体拍成照片本质是从三维的相机坐标转化为二维的平面坐标,这一步称为投影变换。投影可以分为正射投影和透视投影。
- 视口变换(viewport transformation)或窗口变换(windowing transformation):相机拍成的图片最后是要显示在屏幕上,我们需要把二维的图片坐标再转换为电脑屏幕的像素坐标,这一步称为视口变换或窗口变换。
下面这个照相的类比非常地生动形象。

2.1 Viewport Transformation-视口变换
一般来说,我们规定相机沿着 − z -\mathbf{z} −z方向,在观测过程中为了简化会使用canonical view volume(CCV):它是一个正方体, x x x, y y y, z z z坐标都位于 − 1 -1 −1到 1 1 1之间,也即 ( x , y , z ) ∈ [ − 1 , 1 ] 3 (x,y,z)\in[-1,1]^3 (x,y,z)∈[−1,1]3,我们将 x = − 1 x=-1 x=−1投影到电脑屏幕的左侧,将 x = + 1 x=+1 x=+1投影到屏幕的右侧,将 y = − 1 y=-1 y=−1投影到屏幕的底部,将 y = + 1 y=+1 y=+1投影到屏幕的顶部。

如果我们定义屏幕每个像素的长和宽为1,最小的像素中心坐标是 ( 0 , 0 ) (0,0) (0,0),则图像的中心到其边界为 0.5 0.5 0.5,如果屏幕上的像素总长度为 n x n_x nx,总宽度为 n y n_y ny,那么我们可以将canonical view volume(CCV)的 x o y \mathbf{xoy} xoy平面的方形 [ − 1 , 1 ] 2 [-1,1]^2 [−1,1]2映射为长方形 [ − 0.5 , n x − 0.5 ] × [ − 0.5 , n y − 0.5 ] [-0.5,n_x-0.5]\times[-0.5,n_y-0.5] [−0.5,nx−0.5]×[−0.5,ny−0.5]。
注意我们现在假设所有的线都在CCV正方体里,后面这个假设将在讲裁剪的时候放松这个条件。
对于视口变换,我们需要想把CCV正方体的 x o y \mathbf{xoy} xoy平面进行放缩然后将原点平移到屏幕的左下角(CCV的原点在 x o y \mathbf{xoy} xoy正方形的正中心),其可以写作一个二维的变换【这里相当于计算上面的线性映射: − 1 → − 0.5 , 1 → n x − 0.5 ( n y − 0.5 ) -1\rightarrow -0.5,1\rightarrow n_x-0.5(n_y-0.5) −1→−0.5,1→nx−0.5(ny−0.5)】:
[ x screen y screen 1 ] = [ n x 2 0 n x − 1 2 0 n y 2 n y − 1 2 0 0 1 ] [ x canonical y canonical 1 ] \begin{bmatrix} x_{\text {screen }} \\ y_{\text {screen }} \\ 1 \end{bmatrix}=\begin{bmatrix} \frac{n_{x}}{2} & 0 & \frac{n_{x}-1}{2} \\ 0 & \frac{n_{y}}{2} & \frac{n_{y}-1}{2} \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x_{\text {canonical }} \\ y_{\text {canonical }} \\ 1 \end{bmatrix} xscreen yscreen 1 = 2nx0002ny02nx−12ny−11 xcanonical ycanonical 1
这里忽略了 z \mathbf{z} z轴的坐标,因为投影最终和 z z z坐标无关,这里我们可以扩充矩阵(尽管在这里没有用):
M v p = [ n x 2 0 0 n x − 1 2 0 n y 2 0 n y − 1 2 0 0 1 0 0 0 0 1 ] \mathbf{M}_{\mathrm{vp}}=\begin{bmatrix} \frac{n_{x}}{2} & 0 & 0 & \frac{n_{x}-1}{2} \\ 0 & \frac{n_{y}}{2} & 0 & \frac{n_{y}-1}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Mvp= 2nx00002ny0000102nx−12ny−101
2.2 Orthographic Projection Transformation-正射变换
我们通常想把在渲染某个空间区域的几何元素而不是CCV,我们要调整我们的坐标轴的方向来实现正射变换,让坐标轴的 − z -\mathbf{z} −z轴对着物体,让 y \mathbf{y} y轴朝上, x \mathbf{x} x轴按照右手定则定义。我们看到的view volume是一个 [ l , r ] × [ b , t ] × [ f , n ] [l,r]\times[b,t]\times[f,n] [l,r]×[b,t]×[f,n]的box。

关于 l , r , b , y , f , n l,r,b,y,f,n l,r,b,y,f,n的物理含义可以看下面的表格:
{% tabs active:1 align:center %}
| plane | meaning | plane | meaning |
|---|---|---|---|
| x = l x=l x=l | left plane | x = r x=r x=r | right plane |
| y = b y=b y=b | bottom plane | y = t y=t y=t | top plane |
| z = n z=n z=n | near plane | z = f z=f z=f | far plane |
{% endtabs %}
我们同样可以写出变换矩阵把这个box映射为CCV(参考原书公式的6.7,英文原版132页),变换的好处是简化数字在 − 1 -1 −1到 1 1 1之间,方便后续计算:
M orth = [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 2 n − f 0 0 0 0 1 ] [ 1 0 0 − r + l 2 0 1 0 − t + b 2 0 0 1 − n + f 2 0 0 0 1 ] = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 2 n − f − n + f n − f 0 0 0 1 ] \begin{aligned}\mathbf{M}_{\text {orth }}&=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{array}\right]\\&=\begin{bmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\ 0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f} \\ 0 & 0 & 0 & 1 \end{bmatrix}\end{aligned} Morth = r−l20000t−b20000n−f200001 100001000010−2r+l−2t+b−2n+f1 = r−l20000t−b20000n−f20−r−lr+l−t−bt+b−n−fn+f1
现在我们可以转换视角中任意看到的点 ( x , y , z ) (x,y,z) (x,y,z)在像素上看到的位置 ( x p i x e l , y p i x e l , z c a n o n i c a l ) (x_{pixel},y_{pixel},z_{canonical}) (xpixel,ypixel,zcanonical)
[ x pixel y pixel z canonical 1 ] = ( M v p M orth ) [ x y z 1 ] \left[\begin{array}{c} x_{\text {pixel }} \\ y_{\text {pixel }} \\ z_{\text {canonical }} \\ 1 \end{array}\right]=\left(\mathbf{M}_{\mathrm{vp}} \mathbf{M}_{\text {orth }}\right)\left[\begin{array}{c} x \\ y \\ z \\ 1 \end{array}\right] xpixel ypixel zcanonical 1 =(MvpMorth ) xyz1
CCV坐标变换至屏幕坐标直线算法流程:

z \mathbf{z} z坐标的范围是 [ − 1 , 1 ] [-1,1] [−1,1],现在我们还没有用到,这将在z-buffer算法时很有用。
2.3 Camera Transformation-相机变换
当我们需要改变3D视角和观测的方向时,我们需要重新定义观测者的位置和方向(改变相机的放置位置)。可以定义相机坐标系,我们期望的相机的朝向可以由两个向量 g \mathbf{g} g和向量 t \mathbf{t} t来定义,以及一个点 e \mathbf{e} e来表示。
- e \mathbf{e} e:相机位置
- g \mathbf{g} g:观测方向
- t \mathbf{t} t:上视方向
于是我们可以根据上面所说的向量和电定义我们的相机坐标系 u v w \mathbf{uvw} uvw(世界坐标系是 x y z \mathbf{xyz} xyz),其中坐标系的原点就是 e \mathbf{e} e, v \mathbf{v} v轴和 t \mathbf{t} t矢量方向相同, w \mathbf{w} w轴和 − g -\mathbf{g} −g矢量方向相同, u \mathbf{u} u轴根据右手定则确定。
w = − g ∥ g ∥ u = t × w ∥ t × w ∥ v = w × u \begin{aligned} \mathbf{w} & = -\frac{\mathbf{g}}{\|\mathbf{g}\|} \\ \mathbf{u} & = \frac{\mathbf{t} \times \mathbf{w}}{\|\mathbf{t} \times \mathbf{w}\|} \\ \mathbf{v} & = \mathbf{w} \times \mathbf{u} \end{aligned} wuv=−∥g∥g=∥t×w∥t×w=w×u

接下来我们会把世界坐标系的点坐标转换到相机坐标系中。我们可以把变换矩阵分解为两步,先平移再旋转。
由于将坐标系 u v w \mathbf{uvw} uvw转换为坐标系 x y z \mathbf{xyz} xyz的变换矩阵可以看做是
M c a m − 1 = [ u v w e 0 0 0 1 ] \mathbf{M}_{\mathrm{cam}}^{-1}=\left[\begin{array}{cccc} \mathbf{u} & \mathbf{v} & \mathbf{w} & \mathbf{e} \\ 0 & 0 & 0 & 1 \end{array}\right] Mcam−1=[u0v0w0e1]
相机坐标系是要将坐标系 x y z \mathbf{xyz} xyz转换到坐标系 u v w \mathbf{uvw} uvw,于是这等价于对矩阵求一个逆。
M c a m = [ u v w e 0 0 0 1 ] − 1 = [ x u y u z u 0 x v y v z v 0 x w y w z w 0 0 0 0 1 ] [ 1 0 0 − x e 0 1 0 − y e 0 0 1 − z e 0 0 0 1 ] \mathbf{M}_{\mathrm{cam}}=\left[\begin{array}{cccc} \mathbf{u} & \mathbf{v} & \mathbf{w} & \mathbf{e} \\ 0 & 0 & 0 & 1 \end{array}\right]^{-1}=\left[\begin{array}{cccc} x_{u} & y_{u} & z_{u} & 0 \\ x_{v} & y_{v} & z_{v} & 0 \\ x_{w} & y_{w} & z_{w} & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} 1 & 0 & 0 & -x_{e} \\ 0 & 1 & 0 & -y_{e} \\ 0 & 0 & 1 & -z_{e} \\ 0 & 0 & 0 & 1 \end{array}\right] Mcam=[u0v0w0e1]−1= xuxvxw0yuyvyw0zuzvzw00001 100001000010−xe−ye−ze1
世界坐标正式投影变换至屏幕坐标画直线算法流程:

2.4 Perspective Projective Transformations-透视变换
投影变换符合我们的视觉直观,主要体现在有近大远小的特性,平行线相交于一点。在实际的计算机图形中用得更多。

如上图所示,我们从视点 e \mathbf{e} e沿着 g \mathbf{g} g方向看,看到的实际的点的高度为 y y y,反映在观察平面上高度为 y s y_s ys,观察平面距离视点为 d d d,实际的点距离视点为 z z z,根据简单的相似三角形的关系,我们有(这里我们认为 z z z是距离,为正数,而不是坐标意义下的负数):
y s = d z y y_{s}=\frac{d}{z} y ys=zdy
虎书里还提到了线性有理变换,这里把变换矩阵简单写一下(感兴趣可以直接看虎书)
[ x ~ y ~ z ~ w ~ ] = [ a 1 b 1 c 1 d 1 a 2 b 2 c 2 d 2 a 3 b 3 c 3 d 3 e f g h ] [ x y z 1 ] \left[\begin{array}{c} \tilde{x} \\ \tilde{y} \\ \tilde{z} \\ \tilde{w} \end{array}\right]=\left[\begin{array}{cccc} a_{1} & b_{1} & c_{1} & d_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} \\ a_{3} & b_{3} & c_{3} & d_{3} \\ e & f & g & h \end{array}\right]\left[\begin{array}{c} x \\ y \\ z \\ 1 \end{array}\right] x~y~z~w~ = a1a2a3eb1b2b3fc1c2c3gd1d2d3h xyz1
( x ′ , y ′ , z ′ ) = ( x ~ / w ~ , y ~ / w ~ , z ~ / w ~ ) \left(x^{\prime}, y^{\prime}, z^{\prime}\right)=(\tilde{x} / \tilde{w}, \tilde{y} / \tilde{w}, \tilde{z} / \tilde{w}) (x′,y′,z′)=(x~/w~,y~/w~,z~/w~)
上面的第二个公式刚好使用了计算机图形学笔记1-Transformation Matrix-变换*中注意的第二点:齐次坐标的等价性。使用上述的变换可以进行下面的操作:

前面我们已经讲了二维的情况。但是我们实际要处理的是三维的情况。经过投影变换就好像把一个棱台给变成了一个轴平行的box。这将方便我们使用正交投影变换矩阵变成CCV。

这里我们就搬出之前在相机变换所建立的坐标系,我们依然使用 z = n z=n z=n近端平面和 z = f z=f z=f远端平面,并使用 z = n z=n z=n近端平面作为观察平面。需要注意的是,上面的 n n n和 z z z在坐标系定义下都是小于 0 0 0的。对于投影变换后的 x s x_s xs和 y s y_s ys,类似前面二维情况:
y s = n z y x s = n z x y_{s}=\frac{n}{z} y\quad x_{s}=\frac{n}{z} x ys=znyxs=znx
我们可以整理成矩阵的形式:
( x y z 1 ) ⇒ ( n x / z n y / z u n k n o w n 1 ) ≜ ( n x n y u n k n o w n z ) \begin{pmatrix} x\\y\\z\\1 \end{pmatrix}\Rightarrow\begin{pmatrix} nx/z\\ny/z\\\mathrm{unknown}\\1 \end{pmatrix}\triangleq\begin{pmatrix} nx\\ny\\\mathrm{unknown}\\z \end{pmatrix} xyz1 ⇒ nx/zny/zunknown1 ≜ nxnyunknownz
于是我们所要求的投影变换矩阵满足:
P ( x y z 1 ) = ( n x n y u n k n o w n z ) ⇒ P = ( n 0 0 0 0 n 0 0 ? ? ? ? 0 0 1 0 ) \mathbf{P}\begin{pmatrix} x\\y\\z\\1 \end{pmatrix}=\begin{pmatrix} nx\\ny\\\mathrm{unknown}\\z \end{pmatrix}\Rightarrow \mathbf{P} =\left(\begin{array}{cccc} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \end{array}\right) P xyz1 = nxnyunknownz ⇒P= n0?00n?000?100?0
那么 z s z_{s} zs是多少呢?对投影变换我们注意到:
近端平面 z = n z=n z=n的点映射以后点不发生变化。
远端平面 z = f z=f z=f的点映射以后z坐标不变。
根据第(1)点:近端平面 z = n z=n z=n的点映射以后点不发生变化。我们有:
P ( x y n 1 ) = ( x y n 1 ) ≜ ( n x n y n 2 1 ) \mathbf{P}\begin{pmatrix} x\\y\\n\\1 \end{pmatrix}=\begin{pmatrix} x\\y\\n\\1 \end{pmatrix} \triangleq\begin{pmatrix} nx\\ny\\n^2\\1 \end{pmatrix} P xyn1 = xyn1 ≜ nxnyn21
所以 P \mathbf{P} P的第三行形式为 ( 0 0 A B ) \begin{pmatrix} 0\,0\,A\,B \end{pmatrix} (00AB),前两个元素为0是因为该齐次坐标的 z z z坐标为 n 2 n^2 n2,和 x , y x,y x,y的取值无关。我们单独拿出第三行和齐次坐标相乘有:
( 0 0 A B ) ( x y n 1 ) = n 2 ⇒ A n + B = n 2 \begin{pmatrix} 0 & 0 & A & B \end{pmatrix}\begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix}=n^{2}\Rightarrow An+B=n^2 (00AB) xyn1 =n2⇒An+B=n2
根据第(2)点:远端平面 z = f z=f z=f的点映射以后z坐标不变。我们有:
( 0 0 f 1 ) ⇒ ( 0 0 f 1 ) ≜ ( 0 0 f 2 f ) ⇒ A f + B = f 2 \left(\begin{array}{l} 0 \\ 0 \\ f \\ 1 \end{array}\right) \Rightarrow\left(\begin{array}{l} 0 \\ 0 \\ f \\ 1 \end{array}\right)\triangleq\left(\begin{array}{c} 0 \\ 0 \\ f^{2} \\ f \end{array}\right)\Rightarrow Af+B=f^2 00f1 ⇒ 00f1 ≜ 00f2f ⇒Af+B=f2
于是我们有:
{ A n + B = n 2 A f + B = f 2 ⇒ { A = n + f B = − n f \left\{\begin{aligned} &An+B=n^2\\ &Af+B=f^2 \end{aligned}\right.\quad\Rightarrow\quad\left\{\begin{aligned} &A=n+f\\ &B=-nf \end{aligned}\right. {An+B=n2Af+B=f2⇒{A=n+fB=−nf
这样我们就确定了投影变换的变换矩阵:
P = [ n 0 0 0 0 n 0 0 0 0 n + f − f n 0 0 1 0 ] \mathbf{P}=\begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -f n \\ 0 & 0 & 1 & 0 \end{bmatrix} P= n0000n0000n+f100−fn0
经过投影变换最终我们看到坐标发生了如下的变化:
P [ x y z 1 ] = [ n x n y ( n + f ) z − f n z ] ≜ [ n x z n y z n + f − f n z 1 ] \mathbf{P}\left[\begin{array}{l} x \\ y \\ z \\ 1 \end{array}\right]=\left[\begin{array}{c} n x \\ n y \\ (n+f) z-f n \\ z \end{array}\right] \triangleq\left[\begin{array}{c} \frac{n x}{z} \\ \frac{n y}{z} \\ n+f-\frac{f n}{z} \\ 1 \end{array}\right] P xyz1 = nxny(n+f)z−fnz ≜ znxznyn+f−zfn1
有时候我们想把屏幕坐标变换回世界坐标,这时候我们就需要用到 P \mathbf{P} P的逆矩阵:
P − 1 = [ 1 n 0 0 0 0 1 n 0 0 0 0 0 1 0 0 − 1 f n n + f f n ] ≜ [ f 0 0 0 0 f 0 0 0 0 0 f n 0 0 − 1 n + f ] \mathbf{P}^{-1}=\left[\begin{array}{cccc} \frac{1}{n} & 0 & 0 & 0 \\ 0 & \frac{1}{n} & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & -\frac{1}{f n} & \frac{n+f}{f n} \end{array}\right]\triangleq\left[\begin{array}{cccc} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 0 & f n \\ 0 & 0 & -1 & n+f \end{array}\right] P−1= n10000n100000−fn1001fnn+f ≜ f0000f00000−100fnn+f
完整的透视变换包括了正视变换和投影变换的组合,先处理近大远小的投影变换为box,然后把box变回一个CCV。
M p e r = M o r t h P = [ 2 n r − l 0 l + r l − r 0 0 2 n t − b b + t b − t 0 0 0 f + n n − f 2 f n f − n 0 0 1 0 ] \mathbf{M}_{\mathrm{per}}=\mathbf{M}_{\mathrm{orth}} \mathbf{P}=\left[\begin{array}{cccc} \frac{2 n}{r-l} & 0 & \frac{l+r}{l-r} & 0 \\ 0 & \frac{2 n}{t-b} & \frac{b+t}{b-t} & 0 \\ 0 & 0 & \frac{f+n}{n-f} & \frac{2 f n}{f-n} \\ 0 & 0 & 1 & 0 \end{array}\right] Mper=MorthP= r−l2n0000t−b2n00l−rl+rb−tb+tn−ff+n100f−n2fn0
在OpenGL中,这一矩阵的定义可能不一样:
M OpenGL = [ 2 ∣ n ∣ r − l 0 r + l r − l 0 0 2 ∣ n ∣ t − b t + b t − b 0 0 0 ∣ n ∣ + ∣ f ∣ ∣ n ∣ − ∣ f ∣ 2 ∣ f ∣ ∣ n ∣ ∣ n ∣ − ∣ f ∣ 0 0 − 1 0 ] \mathbf{M}_{\text {OpenGL }}=\left[\begin{array}{cccc} \frac{2|n|}{r-l} & 0 & \frac{r+l}{r-l} & 0 \\ 0 & \frac{2|n|}{t-b} & \frac{t+b}{t-b} & 0 \\ 0 & 0 & \frac{|n|+|f|}{|n|-|f|} & \frac{2|f||n|}{|n|-|f|} \\ 0 & 0 & -1 & 0 \end{array}\right] MOpenGL = r−l2∣n∣0000t−b2∣n∣00r−lr+lt−bt+b∣n∣−∣f∣∣n∣+∣f∣−100∣n∣−∣f∣2∣f∣∣n∣0
这里我们使用了 M o r t h \mathbf{M}_{\mathrm{orth}} Morth,随之而来的问题是: M o r t h \mathbf{M}_{\mathrm{orth}} Morth中的 l , r , t , b l,r,t,b l,r,t,b这些值怎么定义呢,它们定义了我们的窗口看到的物体,由于近端平面 z = n z=n z=n的 x x x和 y y y不变,我们这里选择了近端平面 z = n z=n z=n来定义 l , r , t , b l,r,t,b l,r,t,b。
我们最后来看一下从相机坐标经过透视变换到屏幕坐标的算法流程:

2.5 Field-of-View-视场
我们通过 ( l , r , t , b ) (l,r,t,b) (l,r,t,b)和 n n n定义我们的窗口,我们可以进一步简化,如果我们屏幕的中心是原点,那么有:
l = − r , b = − t . \begin{aligned} l & =-r, \\ b & =-t . \end{aligned} lb=−r,=−t.
另外我们可以添加每个像素是正方形的约束,使得图形没有形状的畸变,我们使用的 r r r和 t t t一定要和水平像素数 n x n_x nx和竖直像素数 n y n_y ny成比例:
n x n y = r t \frac{n_{x}}{n_{y}}=\frac{r}{t} nynx=tr
当 n x n_x nx和 n y n_y ny被确定以后,只剩下一个自由度,我们经常使用 θ \theta θ作为视场,下图为垂直视场,它满足关系:
tan θ 2 = t ∣ n ∣ \tan\frac{\theta}{2}=\frac{t}{|n|} tan2θ=∣n∣t

通过确定 n n n和 θ \theta θ,我们就可以计算 t t t来得到更一般的观测系统。
参考资料
- GAMES101-现代计算机图形学入门-闫令琪
- Shirley & Marschner, Fundamentals of Computer Graphics. forth edition
相关文章:

计算机图形学笔记2-Viewing 观测
观测主要解决的问题是如何把物体的三维“模型”变成我们在屏幕所看到的二维“图片”,我们在计算机看到实体模型可以分成这样几步: 相机变换(camera transformation)或眼变换(eye transformation):想象把相机放在任意一个位置来观测物体&#…...
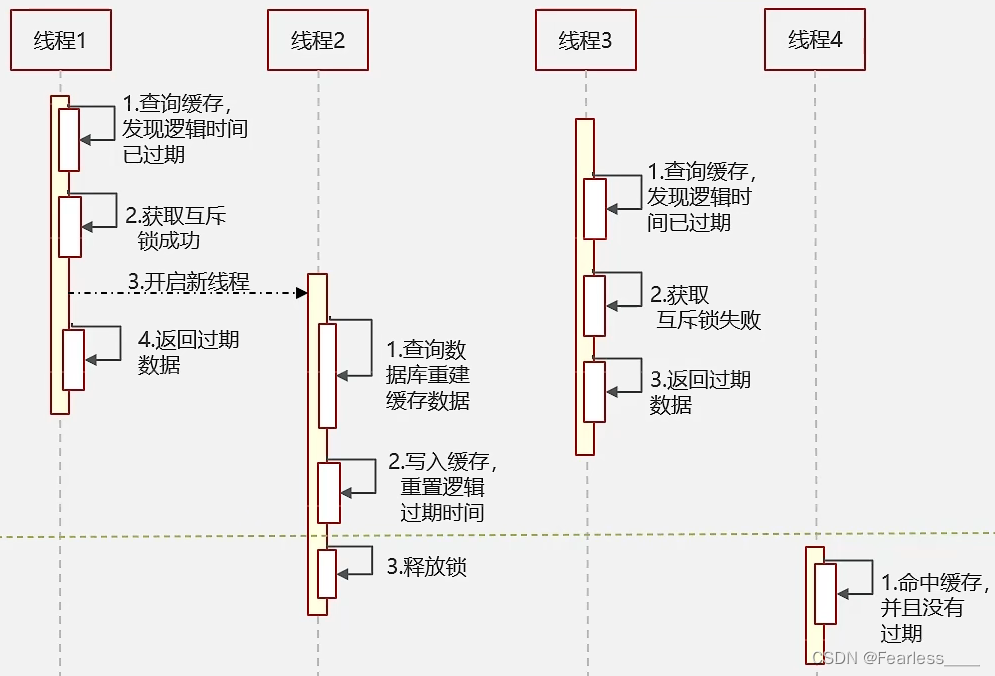
Redis - 三大缓存问题(穿透、击穿、雪崩)
缓存穿透 概念: 查询一个数据库中也不存在的数据,数据库查询不到数据也就不会写入缓存,就会导致一直查询数据库 解决方法: 1. 缓存空数据 如果数据库也查询不到,就把空结果进行缓存 缺点是 - 消耗内存 2. 使用布…...
web自动化测试-PageObject 设计模式
为 UI 页面写测试用例时(比如 web 页面,移动端页面),测试用例会存在大量元素和操作细节。当 UI 变化时,测试用例也要跟着变化, PageObject 很好的解决了这个问题。 使用 UI 自动化测试工具时(包…...
 结构体、map 携带 符号 转成 “\u0026“)
golang json.Marshal() 结构体、map 携带 符号 转成 “\u0026“
问题:数据结构中的值 带有 & > < 等符号,当我们要将 struct map 转成json时,使用 json.Marshal() 函数,此函数会将 值中的 & < > 符号转义 为 类似 "\u0026" 像我们某个结构体中…...
)
【设计模式|行为型】备忘录模式(Memento Pattern)
说明 备忘录模式是一种行为型设计模式,通过捕获一个对象的内部状态,并在该对象之外保存这个状态,以便在需要时恢复对象到原先的状态。备忘录模式包含三个核心角色:。 发起人(Originator):负责…...
的区别是什么?)
Redis与其他缓存解决方案(如Memcached)的区别是什么?
Redis和其他缓存解决方案(如Memcached)在设计理念、功能和特点上有一些区别,以下是它们的主要区别: 数据类型支持:Redis支持多种数据类型(如字符串、哈希表、列表、集合、有序集合等)࿰…...

《面试1v1》Kafka的ack机制
🍅 作者简介:王哥,CSDN2022博客总榜Top100🏆、博客专家💪 🍅 技术交流:定期更新Java硬核干货,不定期送书活动 🍅 王哥多年工作总结:Java学习路线总结…...
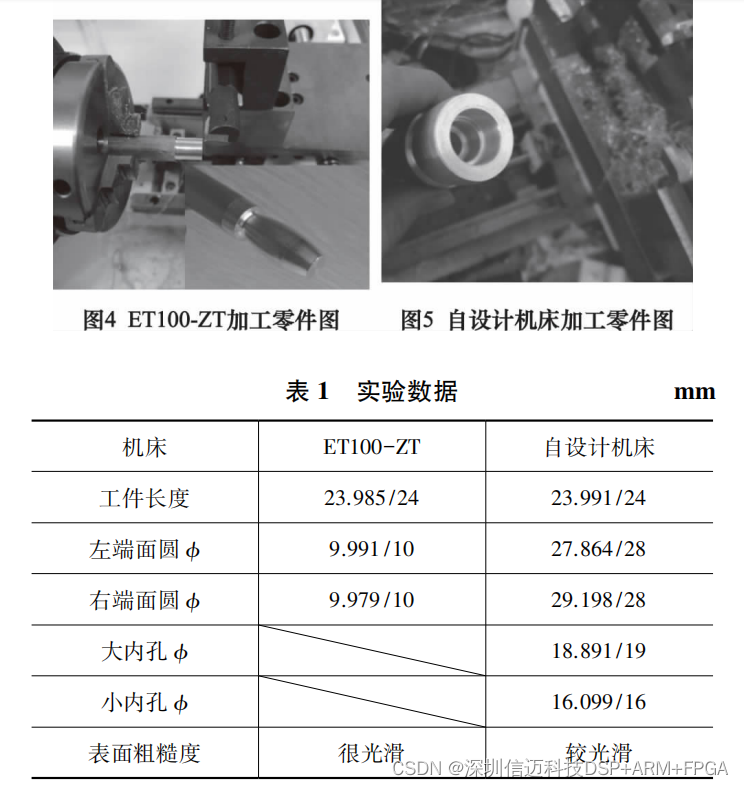
基于双 STM32+FPGA 的桌面数控车床控制系统设计
桌 面数控 设 备 对 小 尺寸零件加工在成 本 、 功 耗 和 占 地 面 积等方 面有 着 巨 大 优 势 。 桌 面数控 设 备 大致 有 3 种 实 现 方 案 : 第 一种 为 微 型 机 床搭 配 传统 数控系 统 , 但 是 桌 面数控 设 备 对 成 本 敏感 ; 第二 种 为 基 于 PC…...
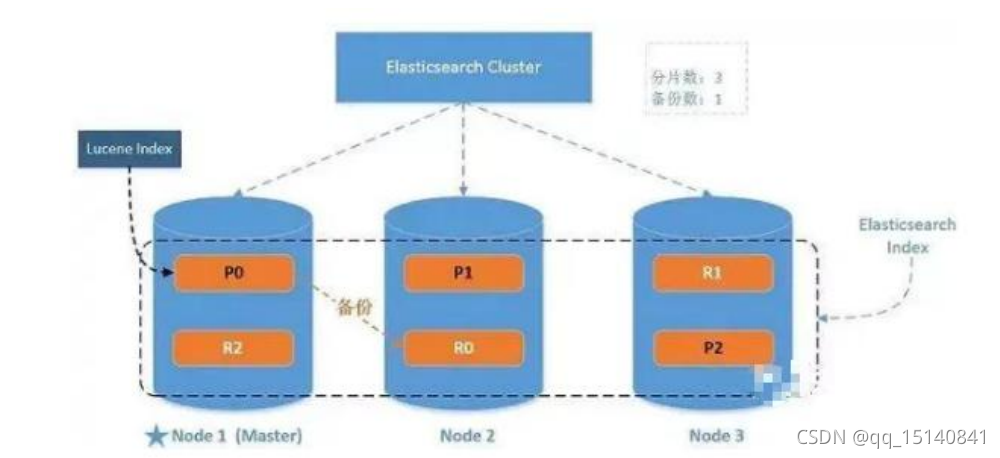
ES-5-进阶
单机 & 集群 单台 Elasticsearch 服务器提供服务,往往都有最大的负载能力,超过这个阈值,服务器 性能就会大大降低甚至不可用,所以生产环境中,一般都是运行在指定服务器集群中 配置服务器集群时,集…...

Java面试准备篇:全面了解面试流程与常见问题
文章目录 1.1 Java面试概述1.2 面试流程和注意事项1.3 自我介绍及项目介绍1.4 常见面试问题 在现代职场中,面试是求职过程中至关重要的一环,特别是对于Java开发者而言。为了帮助广大Java开发者更好地应对面试,本文将提供一份全面的Java面试准…...
Go语言进阶语法八万字详解,通俗易懂
文章目录 File文件操作FileInfo接口权限打开模式File操作文件读取 I/O操作io包 文件复制io包下的Read()和Write()io包下的Copy()ioutil包总结 断点续传Seeker接口断点续传 bufio包bufio包原理Reader对象Writer对象 bufio包bufio.Readerbufio.Writer ioutil包ioutil包的方法示例…...

Apache RocketMQ 远程代码执行漏洞(CVE-2023-37582)
漏洞简介 Apache RocketMQ是一款低延迟、高并发、高可用、高可靠的分布式消息中间件。CVE-2023-37582 中,由于对 CVE-2023-33246 修复不完善,导致在Apache RocketMQ NameServer 存在未授权访问的情况下,攻击者可构造恶意请求以RocketMQ运…...

Kotlin Multiplatform 使用 CocoaPods 创建多平台分发库
Kotlin Multiplatform 支持直接创建Framework 方式和使用CocoaPods 方式创建Framework。 1、不同之处在于创建的时候需要选择不同的方式。 2、使用CocoaPods 方式还需要在 build.gradle(.kts) 文件中添加内容 在build.gradle(.kts) 文件中添加完成后,执行一下文件。…...

前端食堂技术周刊第 92 期:VueConf 2023、TypeChat、向量数据库、Nuxt 服务器组件指南
美味值:🌟🌟🌟🌟🌟 口味:整颗牛油果酸奶 食堂技术周刊仓库地址:https://github.com/Geekhyt/weekly 大家好,我是童欧巴。欢迎来到前端食堂技术周刊,我们先…...

用C语言构建一个手写数字识别神经网络
(原理和程序基本框架请参见前一篇 "用C语言构建了一个简单的神经网路") 1.准备训练和测试数据集 从http://yann.lecun.com/exdb/mnist/下载手写数字训练数据集, 包括图像数据train-images-idx3-ubyte.gz 和标签数据 train-labels-idx1-ubyte.…...
vue关闭ESlint
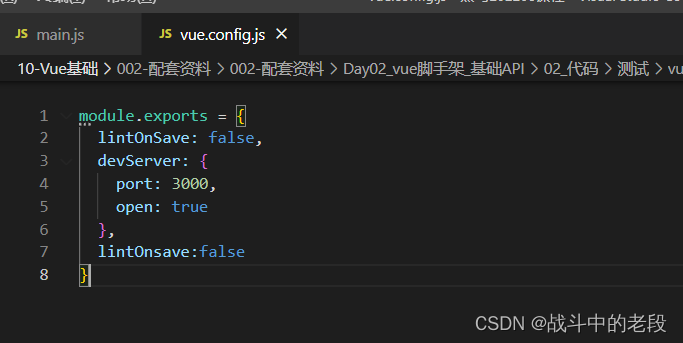
在 vue.config.js里边写上这一句代码 lintOnsave:false写完后重启一下项目...
测试开发人员如何进行局部探索性测试?一张图告诉你
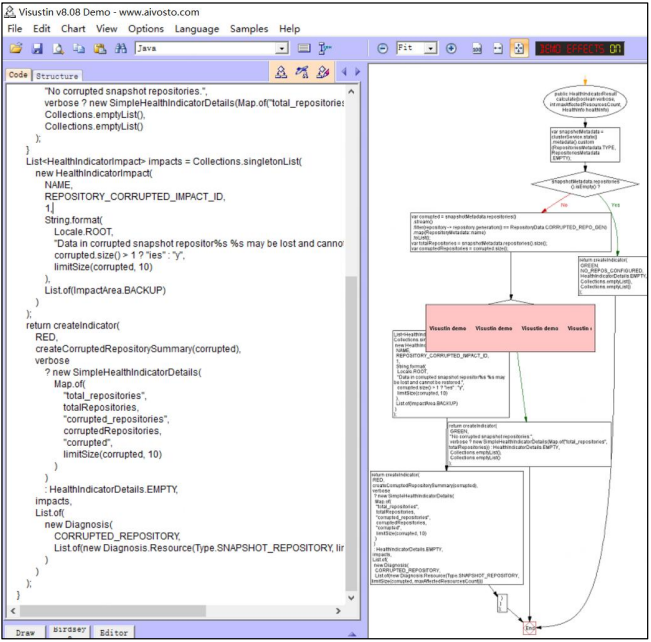
我们都知道全局探索性测试的漫游测试法,也知道局部探索性测试可以从用户输入、状态、代码路径、用户数据和执行环境测试着手点。 那么,如果我们能够获取开发代码,我们怎么从代码入手,进行具体的局部探索性测试呢? 简单…...
CentOS 8 上安装 Nginx
Nginx是一款高性能的开源Web服务器和反向代理服务器,以其轻量级和高效能而广受欢迎。在本教程中,我们将学习在 CentOS 8 操作系统上安装和配置 Nginx。 步骤 1:更新系统 在安装任何软件之前,让我们先更新系统的软件包列表和已安…...
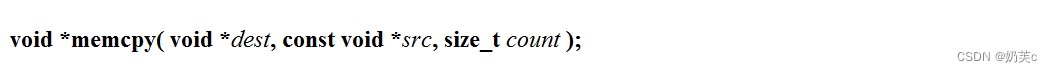
【c语言进阶】字符函数和字符串函数知识总结
字符函数和字符串函数 前期背景求字符串长度函数strlen函数strlen函数三种模拟实现 长度不受限制的字符串函数strcpy函数strcpy函数模拟实现strcat函数strcat函数模拟实现strcmp函数strcmp函数模拟实现 长度受限制的字符串函数strncpy函数strncpy函数模拟实现strncat函数strnca…...

DB2实现正则表达式
DB2实现正则表达式 功能描述 db2 11.1 及以上版本支持正则表达式,但是db2 10.5及以下版本不支持正则表达式,需要手工创建正则表达式函数。 安装与卸载步骤 README.txt2010-07-30IBM IMTE - Project AvalancheAuthor: Alexandre GrancherThis file des…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

RushDB开源程序 是现代应用程序和 AI 的即时数据库。建立在 Neo4j 之上
一、软件介绍 文末提供程序和源码下载 RushDB 改变了您处理图形数据的方式 — 不需要 Schema,不需要复杂的查询,只需推送数据即可。 二、Key Features ✨ 主要特点 Instant Setup: Be productive in seconds, not days 即时设置 :在几秒钟…...
C++中vector类型的介绍和使用
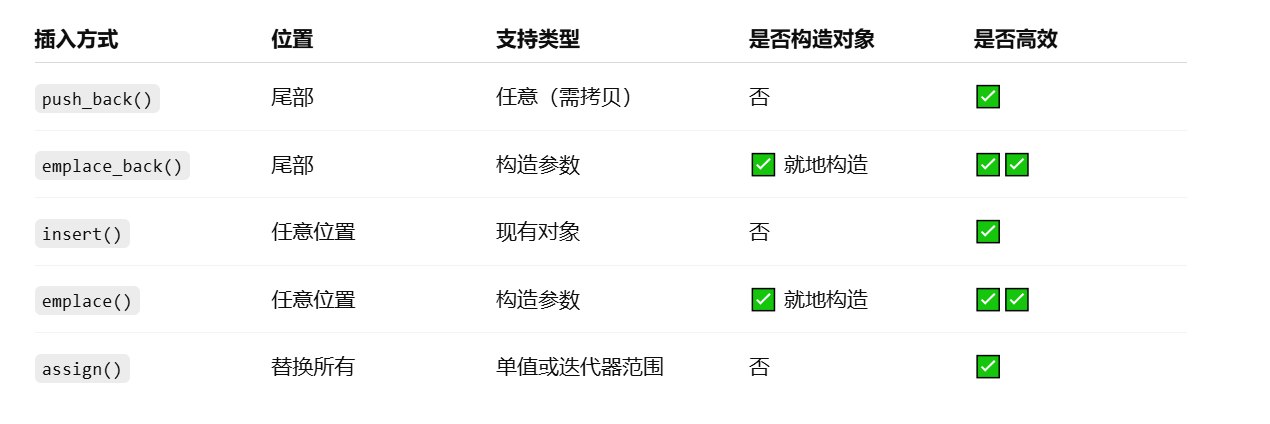
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...

Spring AI中使用ChatMemory实现会话记忆功能
文章目录 1、需求2、ChatMemory中消息的存储位置3、实现步骤1、引入依赖2、配置Spring AI3、配置chatmemory4、java层传递conversaionId 4、验证5、完整代码6、参考文档 1、需求 我们知道大型语言模型 (LLM) 是无状态的,这就意味着他们不会保…...
Xcode 16.2 版本 pod init 报错
Xcode 版本升级到 16.2 后,项目执行 pod init 报错; ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchron…...

MTK-Android12-13 Camera2 设置默认视频画质功能实现
MTK-Android12-13 Camera2 设置默认视频画质功能实现 场景:部分客户使用自己的mipi相机安装到我们主板上,最大分辨率为1280720,但是视频画质默认的是640480。实际场景中,在默认视频分辨率情况下拍出来的视频比较模糊、预览也不清晰…...
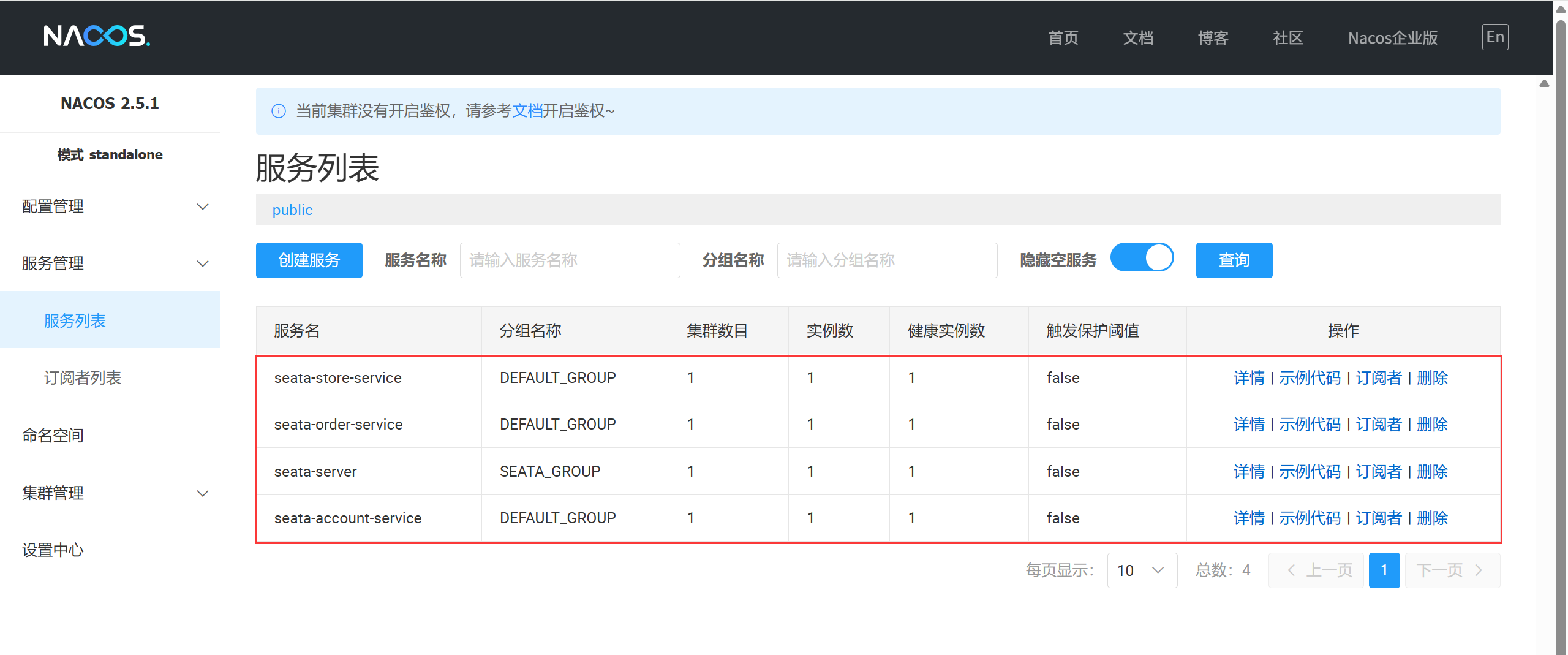
Spring Cloud Alibaba Seata安装+微服务实战
目录 介绍核心功能三层核心架构安装微服务实战创建三个业务数据库编写库存和账户两个Feign接口订单微服务 seata-order-service9701库存微服务 seata-store-service9702账户微服务 seata-account-service9703测试结果 总结 介绍 Spring Cloud Alibaba Seata 是一款开源的分布式…...
