IP隧道技术原理
简介
IP隧道技术是一种将一个协议的数据包封装在另一个协议的数据包中进行传输的技术。在网络通信中,不同的网络协议之间可能存在不兼容的情况,这时候就需要使用IP隧道技术来解决这个问题。
原理
IP隧道技术的原理是将一个协议的数据包封装在另一个协议的数据包中进行传输。例如,将IPv6数据包封装在IPv4数据包中进行传输。这样做的好处是可以在不支持IPv6的网络中传输IPv6数据包,同时也可以在IPv6网络中传输IPv4数据包。
实现
IP隧道技术的实现需要两个隧道端点,分别是发送端和接收端。发送端将要传输的数据包封装在隧道协议的数据包中,然后将封装后的数据包发送给接收端。接收端收到数据包后,将隧道协议的数据包解封装,然后将原始数据包发送给目标设备。
应用
IP隧道技术的应用非常广泛,例如在VPN中就广泛使用了IP隧道技术。VPN是一种通过公共网络建立私有网络的技术,它可以将不同地区的网络连接在一起,形成一个虚拟的私有网络。在VPN中,IP隧道技术可以将私有网络中的数据包封装在公共网络的数据包中进行传输,从而保证数据的安全性和可靠性。
除了在VPN中,IP隧道技术还可以用于IPv6的部署。由于IPv6的普及率较低,很多网络设备还不支持IPv6协议。在这种情况下,可以使用IP隧道技术将IPv6数据包封装在IPv4数据包中进行传输,从而实现IPv6的部署。
价值
IP隧道技术是一种非常重要的网络技术,它可以解决不同协议之间的兼容性问题,同时也可以保证数据的安全性和可靠性。在未来的网络发展中,IP隧道技术将会发挥越来越重要的作用。
相关文章:

IP隧道技术原理
简介 IP隧道技术是一种将一个协议的数据包封装在另一个协议的数据包中进行传输的技术。在网络通信中,不同的网络协议之间可能存在不兼容的情况,这时候就需要使用IP隧道技术来解决这个问题。 原理 IP隧道技术的原理是将一个协议的数据包封装在另一个协议…...
Docker私有仓库
Docker私有仓库 Docker官方的Docker hub(https://hub.docker.com)是一个用于管理公共镜像的仓库,我们可以从上面拉取镜像到本地,也可以把我们自己的镜像推送上去。但是,有时候我们的服务器无法访问互联网,…...

LLM微调 | Prefix-Tuning, Prompt-Tuning, P-tuning, P-tuning-v2
🔥 下面我只是分析讲解下这些方法的原理以及具体代码是怎么实现的,不对效果进行评价,毕竟不同任务不同数据集效果差别还是挺大的。 文章目录 0、hard prompt & soft prompt区别1、Prefix-Tuning2、Prompt-Tuning3、P-tuning4、P-tuning-v25、来看看adapter,lora,pref…...

Ansible 的脚本 --- playbook 剧本
目录 playbook 剧本 playbooks 本身由以下各部分组成 定义、引用变量 指定远程主机sudo切换用户 when条件判断 迭代 Templates 模块 1.先准备一个以 .j2 为后缀的 template 模板文件,设置引用的变量 2.修改主机清单文件,使用主机变量定义一个变…...

CSP-J模拟赛 / 买文具
限制条件 时间限制: 1000 ms, 空间限制: 256 MB 输入文件: pen.in, 输出文件:pen.out 题目描述 开学啦,为了准备新学期的课程学习,小贝到商店买文具。小贝买完文具回家,告诉妈妈说她买了钢笔、圆珠笔和铅笔总共x支,…...

leecode算法--每日一题1
二分查找 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。 前提条件必须满足: 目标数组必须是有序数组 所以…...
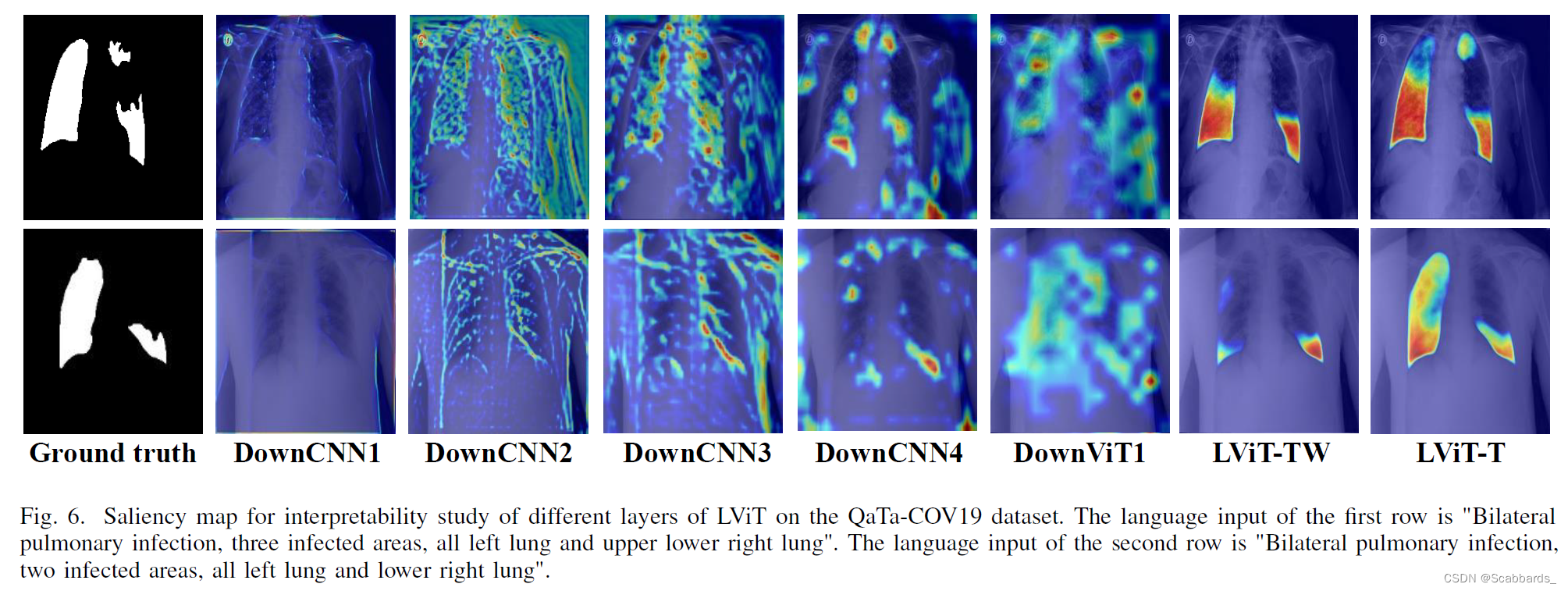
LViT:语言与视觉Transformer在医学图像分割
论文链接:https://arxiv.org/abs/2206.14718 代码链接:GitHub - HUANGLIZI/LViT: This repo is the official implementation of "LViT: Language meets Vision Transformer in Medical Image Segmentation" (IEEE Transactions on Medical I…...
!!!)
蓝桥杯上岸每日N题 第五期(山)!!!
蓝桥杯上岸每日N题第五期 ❗️ ❗️ ❗️ 同步收录 👇 蓝桥杯Java 省赛B组(初赛)填空题 大家好 我是寸铁💪 冲刺蓝桥杯省一模板大全来啦 🔥 蓝桥杯4月8号就要开始了 🙏 距离蓝桥杯省赛倒数第3天 ❗️ ❗️ ❗️ 还没背熟模…...
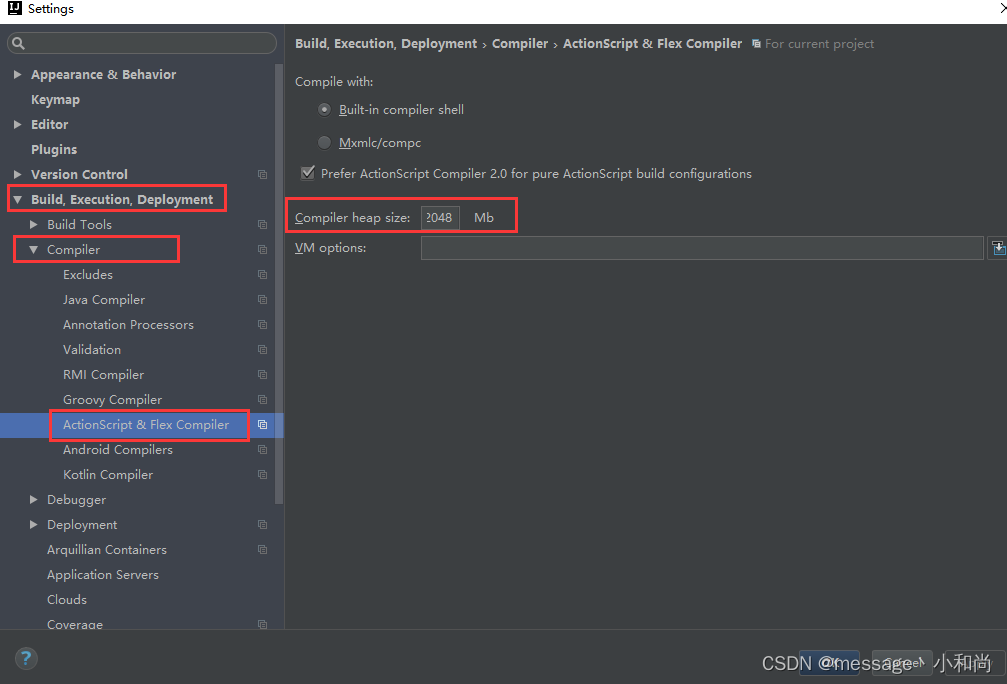
IDEA Writing classes... 比较慢
IDEA配置修改如下: 1、File -> Settings… 2、Build,Execution,Deployment -> Compiler Build process heap size 配置为 20483、Build,Execution,Deployment -> Compiler -> ActionScript & Flex C…...
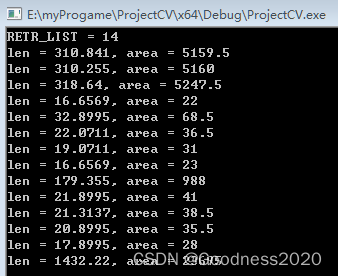
opencv中轮廓相关属性
一、介绍 findContours() :The function retrieves contours from the binary image。 二、代码 void main() {Mat src imread("match00.bmp", IMREAD_GRAYSCALE);Mat mask;threshold(src, mask, 128, 255, cv::THRESH_BINARY_INV);Mat element cv::g…...
Leetcode 144. 二叉树的前序遍历
题目描述 题目链接:https://leetcode.cn/problems/binary-tree-preorder-traversal/description/ 代码实现 class Solution {List<Integer> l new ArrayList<>();public List<Integer> preorderTraversal(TreeNode root) {preoder(root);re…...
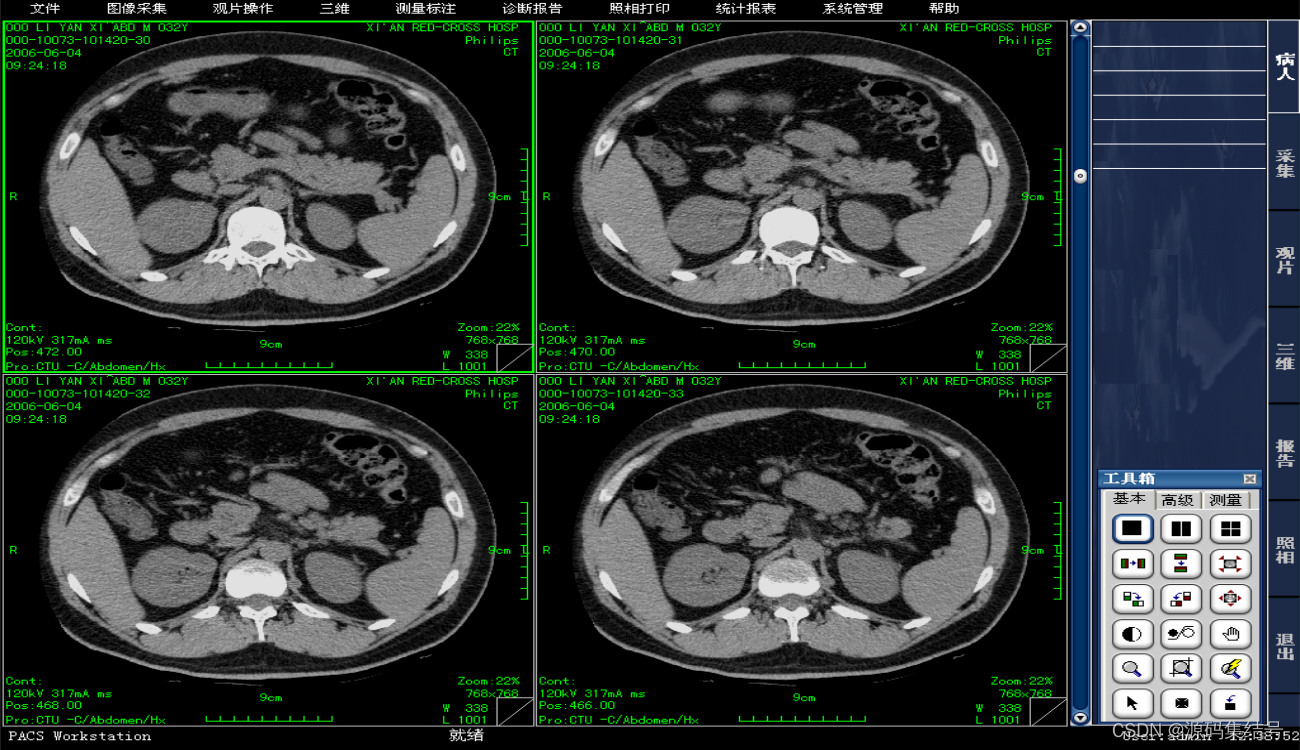
医学影像PACS系统源码:多功能服务器和阅片系统
PACS系统是以最新的IT技术为基础,遵循医疗卫生行业IHE/DICOM3.0和HL7标准,开发的多功能服务器和阅片系统。通过简单高性能的阅片功能,支持繁忙时的影像诊断业务,拥有保存影像的院内Web传输及离线影像等功能,同时具有备…...
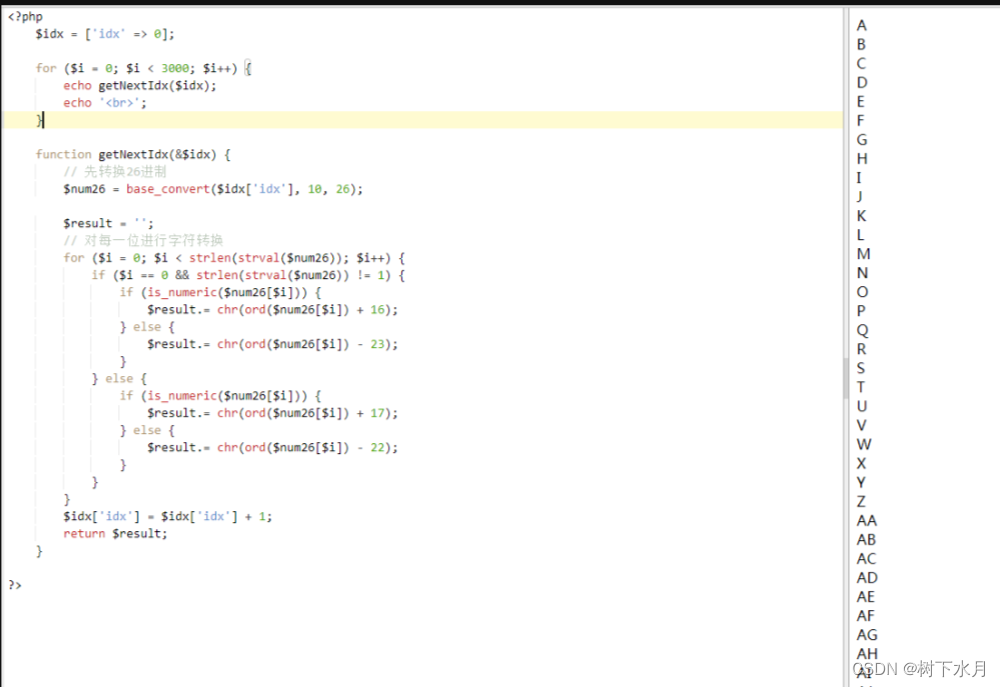
php 生成连续递增的Excel列索引 可以控制多少列
今天遇到需要生成对应的下拉,下拉的类 需要PHP 输出一个数组 如 A、B、C、D 到Z 列后 Excel 的列就变成 AA 、AB、 AC 依次类推 查询得知 Excel 最大列数 16384 最大行数 1048576 下面演示3000列或行 <?php$idx [idx > 0];for ($i …...

Openstack等私有云
1 OpenStack 计算:部署管理虚拟机存储:块存储 Cinder 和 对象存储 Swift网路:管理网络身份:管理用户和权限镜像:管理镜像用于快速部署新的虚拟机仪表盘:Web界面 2 RAID 如果使用的软件已经在多个硬件设备…...
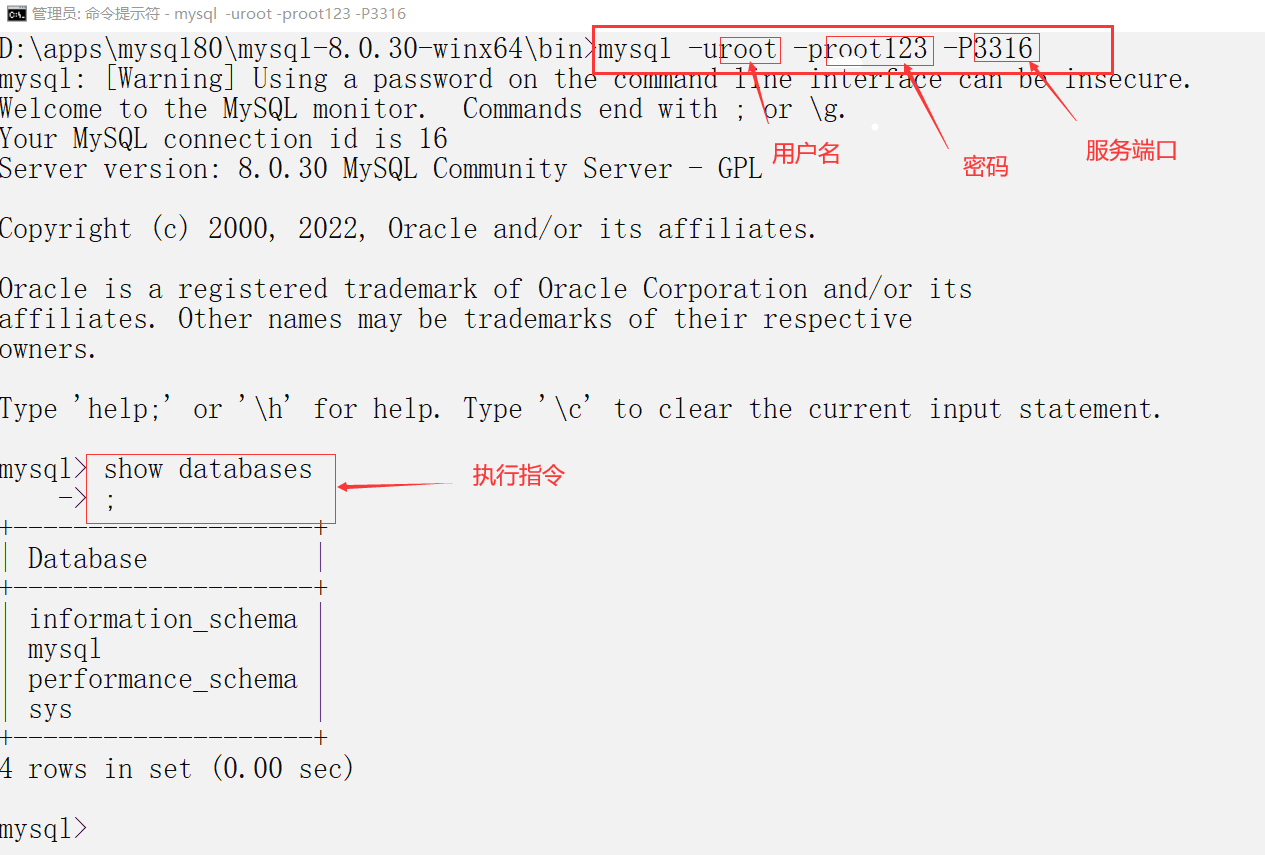
MySQL 8.0详细安装配置教程
一. 前言 MySQL是目前最为流行的开源数据库产品,是完全网络化跨平台的关系型数据库系统。它起初是由瑞典MySQLAB公司开发,后来被Oracle公司收购,目前属于Oracle公司。因为开源,所以任何人都能从官网免费下载MySQL软件,…...
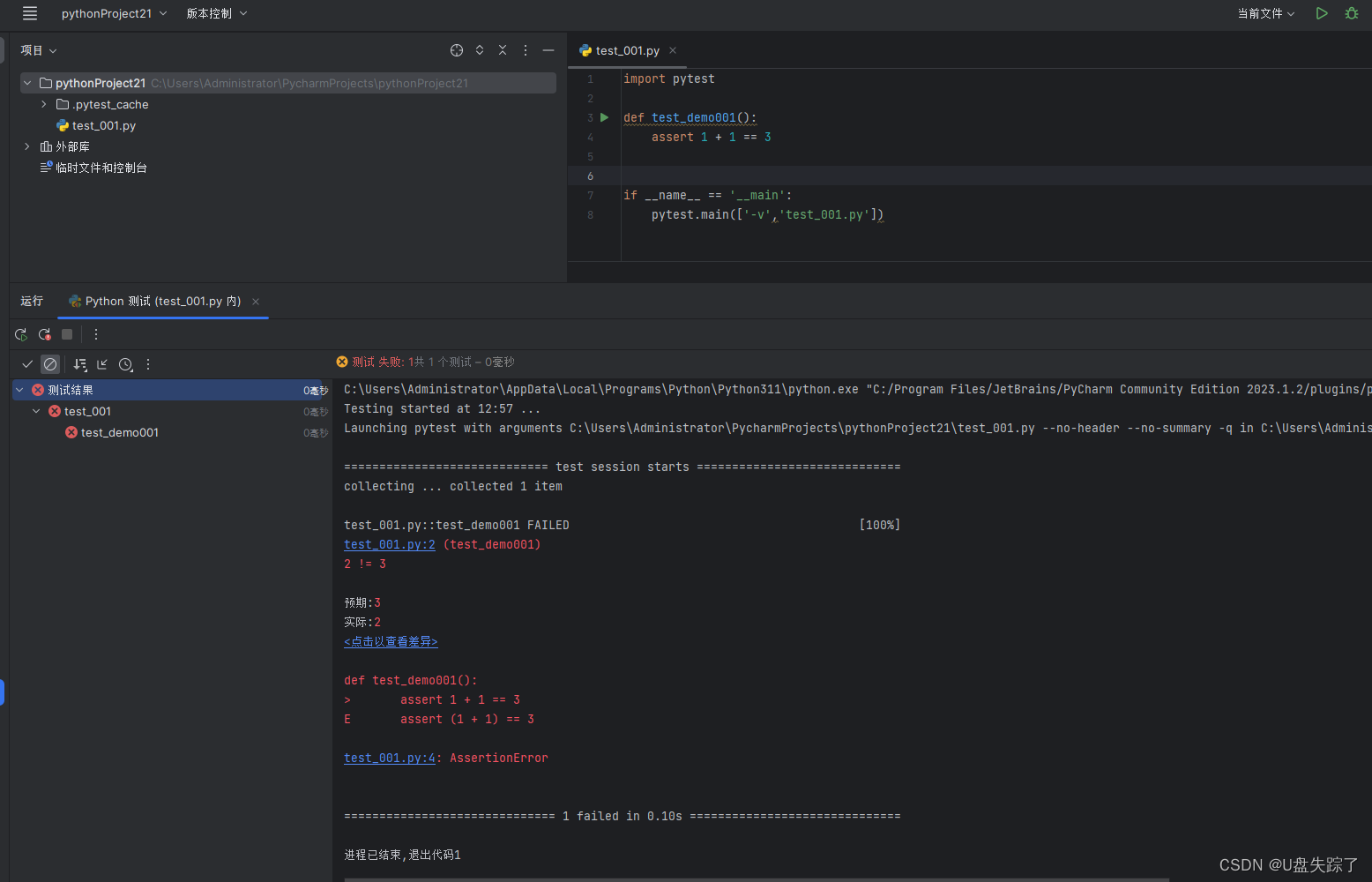
pytest 入门
1,安装pytest 打开终端或命令提示符窗口,在终端中运行以下命令来安装pytest: pip install pytestpip install -i https://pypi.tuna.tsinghua.edu.cn/simple pytest 确保您的系统上已经安装了Python。您可以在终端中运行以下命令来检查Python的安装情况: pytest --version…...

分布式缓存数据一致性-解决方案
如果是用户维度,并发几率小(用户修改订单)。不需要考虑一致性问题,缓存数据加上过期时间,每隔一段时间出发读数据,主动更新缓存即可。(缓存过期删除数据,触发读请求主动更新…...

Java设计模式-享元模式
享元模式 1.享元模式含义 享元模式,运用共享技术有效地支持大量细粒度的对象。 其实享元模式很好理解,就是共享元数据的意思。比如一个小狗类对象,里面的属性有头,耳朵,眼睛,毛色这几个属性,…...
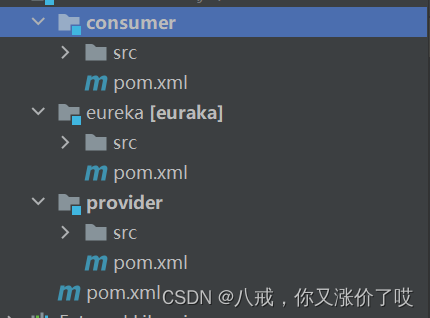
idea模块的pom.xml被划横线,不识别的解决办法
目录 问题: 解决办法: 1.打开设置 2. 取消勾选 3.点击确认 4.解决 问题提出: 写shi山的过程中,给模块取错名字了,改名的时候不知道点到了什么,一个模块的pom.xml变成灰色了࿰…...

ffmpeg 中 av_log 是怎样工作的?
---------------------------------------- author: hjjdebug date: 2023年 07月 27日 星期四 14:56:38 CST descriptor: ffmpeg 中 av_log 是怎样工作的? ---------------------------------------- av_log 功能其实只是添加了颜色,LOG级别,及log上下文名称,没有添加时间,函…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
