HDU 6391 组合数学 + DP
题意
传送门 HDU 6391 Lord Li’s problem
题解
仅考虑 S i ≠ T i S_i\neq T_i Si=Ti 的数量 m m m,最后答案除以 ( n m ) \binom{n}{m} (mn) 即可。考虑 X X X 的排列,最后答案除以 k ! k! k! 即可。
d p [ i + 1 ] [ j ] dp[i+1][j] dp[i+1][j] 代表考虑 X 0 ⋯ X i X_0\cdots X_i X0⋯Xi,这些数字异或和中 1 的数量为 j j j 情况下方案的数量。令 a , b a,b a,b 分别为将 X i X_i Xi 异或进来后,异或和为 0 和 1 的数量,对应的贡献为 d p [ i ] [ j ] ⋅ ( j a ) ⋅ ( n − j b ) dp[i][j]\cdot\binom{j}{a}\cdot\binom{n-j}{b} dp[i][j]⋅(aj)⋅(bn−j)。 X i X_i Xi 可以为任意数字,那么要从 d p [ i + 1 ] [ j ] dp[i+1][j] dp[i+1][j] 中减去 X i X_i Xi 之前出现过的情况,对应的贡献为 d p [ i − 1 ] [ j ] ⋅ i ⋅ [ ( n 3 ) − ( i − 1 ) ] dp[i-1][j]\cdot i\cdot[\binom{n}{3}-(i-1)] dp[i−1][j]⋅i⋅[(3n)−(i−1)]。单个样例时间复杂度 O ( n k ) O(nk) O(nk)。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
constexpr int MOD = 19260817;
constexpr int N = 42;
ll fac[N], inv[N], invf[N];int main() {ios::sync_with_stdio(false);cin.tie(nullptr);fac[0] = invf[0] = 1;fac[1] = inv[1] = invf[1] = 1;for (int i = 2; i < N; ++i) {fac[i] = fac[i - 1] * i % MOD;inv[i] = (MOD - MOD / i) * inv[MOD % i] % MOD;invf[i] = invf[i - 1] * inv[i] % MOD;}auto get = [&](int n, int m) -> ll {if (n < 0 || m < 0 || n < m) {return 0;}return fac[n] * invf[m] % MOD * invf[n - m] % MOD;};auto power = [&](ll x, int n) -> ll {ll res = 1;while (n > 0) {if (n & 1) {(res *= x) %= MOD;}(x *= x) %= MOD, n >>= 1;}return res;};int n, k, tt = 0;while (cin >> n >> k) {tt += 1;if (n == 0 && k == 0) {break;}string s, t;cin >> s >> t;int m = 0;for (int i = 0; i < n; ++i) {m += s[i] != t[i];}vector<vector<ll>> dp(k + 1, vector<ll>(n + 1));dp[0][0] = 1;for (int i = 0; i < k; ++i) {for (int j = 0; j <= n; ++j) {for (int a = 0; a <= 3; ++a) {int b = 3 - a;int nxt = j + (b - a);if (0 <= nxt && nxt <= n) {(dp[i + 1][nxt] += dp[i][j] * get(j, a) % MOD * get(n - j, b) % MOD) %= MOD;}}}if (i - 1 >= 0) {for (int j = 0; j <= n; ++j) {dp[i + 1][j] -= dp[i - 1][j] * i % MOD * (get(n, 3) - (i - 1)) % MOD;(dp[i + 1][j] += MOD) %= MOD;}}}ll res = dp[k][m];(res *= invf[k]) %= MOD;(res *= power(get(n, m), MOD - 2)) %= MOD;cout << "Case #" << tt << ": " << res << '\n';}return 0;
}
相关文章:

HDU 6391 组合数学 + DP
题意 传送门 HDU 6391 Lord Li’s problem 题解 仅考虑 S i ≠ T i S_i\neq T_i SiTi 的数量 m m m,最后答案除以 ( n m ) \binom{n}{m} (mn) 即可。考虑 X X X 的排列,最后答案除以 k ! k! k! 即可。 d p [ i 1 ] [ j ] dp[i1][j] dp[…...

StopWatch与ThreadLocal
目录 1、StopWatch 1、1作用: 1、2方法: 1、3使用方法 2、ThreadLocal 2、1什么是ThreadLocal 2、2简单例子 2、3使用ThreadLocal带来的四个好处 2、4主要方法 2、5ThreadLocal内存泄漏问题 1、StopWatch 1、1作用: 统计代码块耗时时…...

20. 有效的括号
给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串是否有效。 有效字符串需满足: 左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合。 每个右括号都有一个对应的相同类型的左括…...
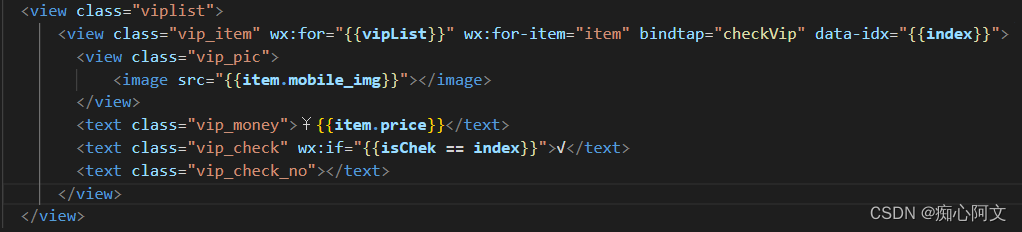
微信小程序原生写法传递参数
微信小程序原生写法传递参数 data-xxx 自定义参数名 ,接收参数:方法(变量名) checkVip:function(event) {let that thisconsole.log(event,event)console.log(event.currentTarget.dataset.idx,index)let index Number(eve…...
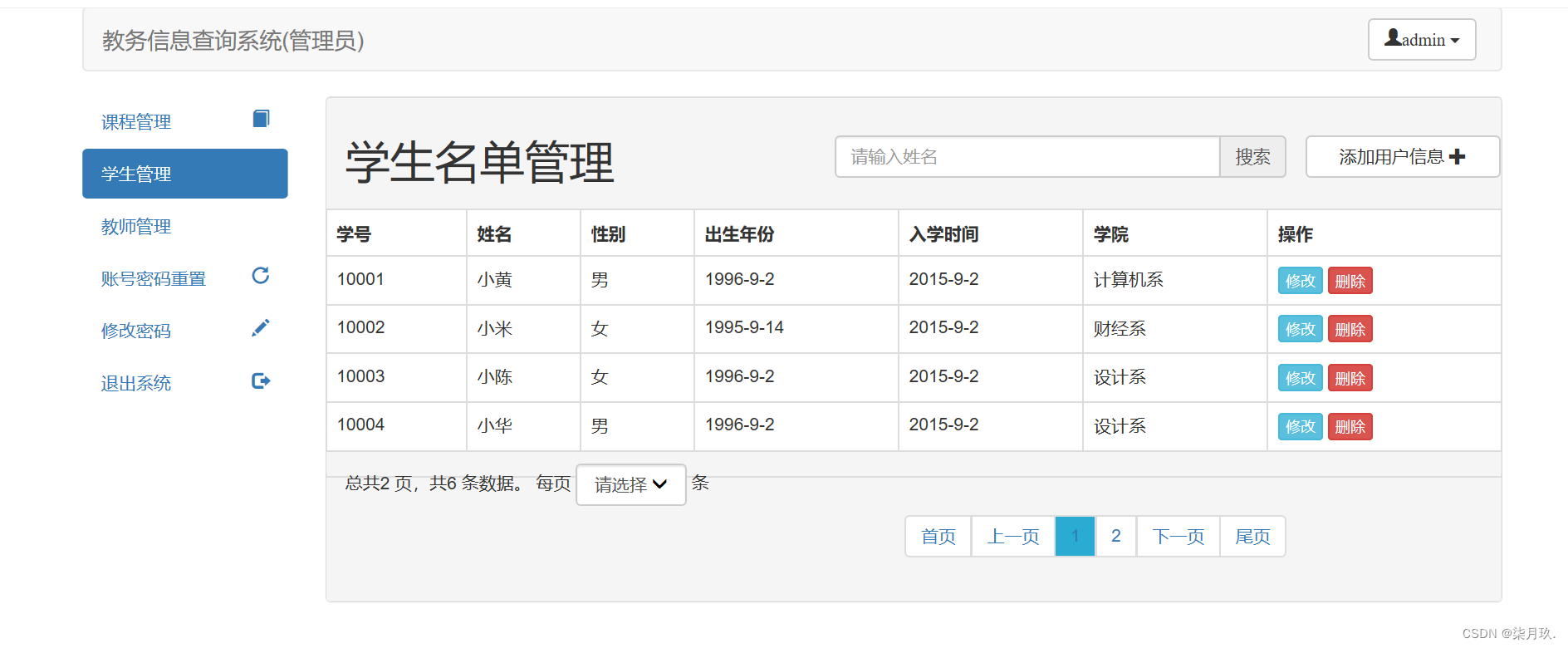
JavaWeb+jsp+Tomcat的教务查询系统
点击以下链接获取源码: https://download.csdn.net/download/qq_64505944/88134601?spm1001.2014.3001.5503 jsp/tomcat7.05/MySQL5.7或8版本/ssm框架/spring/ Web框架:SpringBoot/ORM框架:Mybatis/安全框架:Shiro/分页插件&am…...

C# FTP下载 采用Ssh.Net方式
不要再用FTPClient了 nuget下载Ssh.Net 然后代码如下: /// <summary>/// SFTP操作类/// </summary>public class SFTPHelper{#region 字段或属性private SftpClient sftp;/// <summary>/// SFTP连接状态/// </summary>public bool Conne…...
【C++】做一个飞机空战小游戏(三)——模块化程序设计
[导读]本系列博文内容链接如下: 【C】做一个飞机空战小游戏(一)——使用getch()函数获得键盘码值 【C】做一个飞机空战小游戏(二)——利用getch()函数实现键盘控制单个字符移动【C】做一个飞机空战小游戏(三)——模块化程设设计 在前两讲当中,介绍了利用…...
Django使用WebSocket
1、websocket 相关 实现一个系统,20 个用户同时打开网站,呈现出来一个群聊界面 解决方案 轮询:让浏览器每隔2s向后台发送一次请求,缺点:延迟,请求太多网站压力大 长轮询:客户端向服务端发送请…...

看完这篇 教你玩转渗透测试靶机Vulnhub——HarryPotter:Nagini
Vulnhub靶机HarryPotter:Nagini渗透测试详解 Vulnhub靶机介绍:Vulnhub靶机下载:Vulnhub靶机安装:Vulnhub靶机漏洞详解:①:信息收集:②:漏洞发现:③:SSRF漏洞利用…...

IPO要收紧?业内人士未予以完全确认
“IPO全面收紧、吃穿住等行业标的基本劝退(除非行业龙头)、科创板第五套标准暂停受理……”在上周末,一篇关于IPO收紧的“小作文”在投行圈内疯狂转发。 距离全面注册制正式实施已过去了5个半月,IPO节奏是否在发生较大变化&#…...

stable difussion Pytorch实现与测试
引言: Stable Diffusion是目前最火的AI绘画工具之一,它是一个免费开源的项目,可以被任何人免费部署和使用。通过Stable Diffusion,可以很轻松的通过文字描述,生成对应的图片。由于它是一个开源项目,开源社区(如:GitHub)中有很多插件和训练好的模型,我们可以直接使用。…...

Redis简述
Redis是什么Redis数据类型Redis应用场景缓存计数器分布式会话排行榜最新列表分布式锁消息队列 Redis出现的问题穿透击穿雪崩 Redis为什么速度快 Redis是什么 redis是一种高速缓存数据库 Redis数据类型 string hash list set zset Redis应用场景 缓存 Redis作为缓存层&…...

Redis 操作List
【分布式】Redis 分布式之List_redissonclient.getlist_比嗨皮兔的博客-CSDN博客 说明 配置文件参考:https://blog.csdn.net/qq_38428623/article/details/123217001?utm_sourceapp&app_version5.1.1&codeapp_1562916241&uLinkIdusr1mkqgl919blen ——…...

多个List 合并变成一个List+一个List 根据某个字段相等的另一个字段相加,并排序变成新的List
List<CurveTimeAndValueDomain> curves new ArrayList<>();for (int i 0; i < columnNames.size(); i){if (columnNames.get(i).equals(PlantConstant.TENDOWNFX) || columnNames.get(i).equals(PlantConstant.TENDOWNQP)) {//10千伏以下 数据 进行缓慢处理cu…...
华为流程体系:流程架构「OES方法」
目录 内容简介 OES方法 端到端的流程 专栏列表 CSDN学院 作者简介 内容简介 今天继续来谈谈华为流程体系中的流程架构。 在前期的内容已经介绍过 POS 流程架构的方法。 这里就先回顾一下 POS 方法的相关内容: 关于 POS,大家可以参看上面的这张图…...

c# 创建一个未定义类的临时对象列表
使用场景:要使用的数据太多,列表/字典无法满足需求,需要传入对象,但是又不想创建模型 new[] 是一种用于创建匿名类型数组的写法。它是 C# 中的一种语法糖,用于简化数组的初始化过程。 在下面代码示例中,ne…...

el-button增加下载功能
vue3和element-plus <el-uploadv-model:file-list"fileList"action"/api/upload"multiple:limit"1":headers"headers" ><el-button type"primary">选择文件</el-button><template #file"{ file …...
prometheus和cAdvisor组合
文章目录 docker内部署PromethuesPrometheuscAdvisorPrometheus和cAdvisor关系配置 docker内部署Promethues Prometheus Prometheus是一个开源的系统监控和报警工具,由SoundCloud开发并在2012年捐赠给了Cloud Native Computing Foundation (CNCF)。它被广泛用于监…...
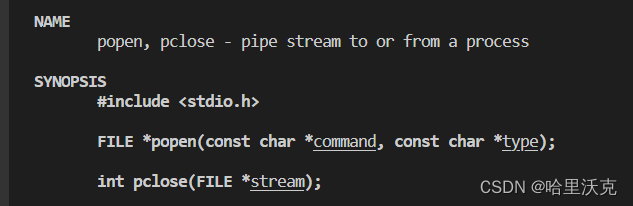
计算机网络(2) --- 网络套接字UDP
计算机网络(1) --- 网络介绍_哈里沃克的博客-CSDN博客https://blog.csdn.net/m0_63488627/article/details/131967378?spm1001.2014.3001.5501 目录 1.端口号 2.TCP与UDP协议 1.TCP协议介绍 1.TCP协议 2.UDP协议 3.理解 2.网络字节序 发送逻辑…...
Idea 结合docker-compose 发布项目
Idea 结合docker-compose 发布项目 这里写目录标题 Idea 结合docker-compose 发布项目Docker 开启远程访问功能 添加相应端口配置IDEA 链接Docker配置项目 docker-compose.yml本地还需要安装 dockerwin11 安装本地Docker 可能存在问题 Linux内核不是最新 Docker 开启远程访问功…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
