第十三章 利用PCA简化数据
文章目录
- 第十三章 利用PCA简化数据
- 13.1降维技术
- 13.2PCA
- 13.2.1移动坐标轴
- 13.2.2在NumPy中实现PCA
- 13.3利用PCA对半导体制造数据降维
第十三章 利用PCA简化数据
PCA(Principal Component Analysis,主成分分析)是一种常用的降维技术,用于将高维数据集转换为低维的表示,同时保留尽可能多的数据信息。它的主要原理是通过线性变换将原始数据投影到一个新的坐标系中,使得数据在新坐标系下的方差最大化。这样,数据的主要特征就能够通过少数几个主成分来表示,从而达到降维的效果。
13.1降维技术
对数据进⾏简化还有如下⼀系列的原因:
- 使得数据集更易使⽤;
- 降低很多算法的计算开销;
- 去除噪声;
- 使得结果易懂
常见的降维技术:
- 主成分分析(PCA):在PCA中,数据从原来的坐标系转换到了新的坐标系,新坐标系的选择是由数据本身决定的。第⼀个新坐标轴选择的是原始数据中⽅差最⼤的⽅向,第二个新坐标轴的选择和第⼀个坐标轴正交且具有最⼤⽅差的⽅向。该过程⼀直重复,重复次数为原始数据中特征的数⽬。我们会发现,⼤部分⽅差都包含在最前⾯的⼏个新坐标轴中。
- 因⼦分析(Factor Analysis)。在因⼦分析中,我们假设在观察数据的⽣成中有⼀些观察不到的隐变量(latent variable)。假设观察数据是这些隐变量和某些噪声的线性组合。那么隐变量的数据可能⽐观察数据的数⽬少,也就是说通过找到隐变量就可以实现数据的降维。因⼦分析已经应⽤于社会科学、⾦融和其他领域中了。
- 独⽴成分分析(Independent Component Analysis,ICA)。ICA假设数据是从N个数据源⽣成的,这⼀点和因⼦分析有些类似。假设数据为多个数据源的混合观察结果,这些数据源之间在统计上是相互独⽴的,⽽在PCA中只假设数据是不相关的。同因⼦分析⼀样,如果数据源的数⽬少于观察数据的数⽬,则可以实现降维过程。
13.2PCA
主成分分析
- 优点:降低数据的复杂性,识别最重要的多个特征。
- 缺点:不⼀定需要,且可能损失有⽤信息。
适⽤数据类型:数值型数据。
13.2.1移动坐标轴
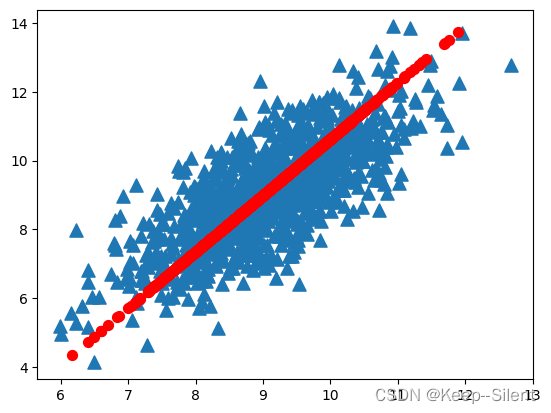
考虑下图,要求画出一条直线,尽可能覆盖这些点。

在PCA中,我们对数据的坐标进⾏了旋转,该旋转的过程取决于数据的本⾝。第⼀条坐标轴旋转到覆盖数据的最⼤⽅差位置,即下图中的红直线
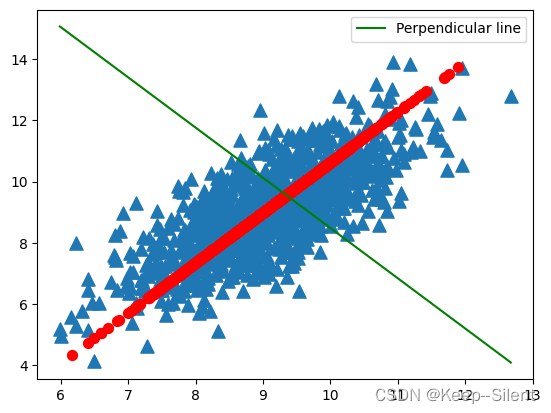
在选择了覆盖数据最⼤差异性的坐标轴之后,我们选择了第二条坐标轴。假如该坐标轴与第⼀条坐标轴正交,它就是覆盖数据次大差异性的坐标轴。如下图
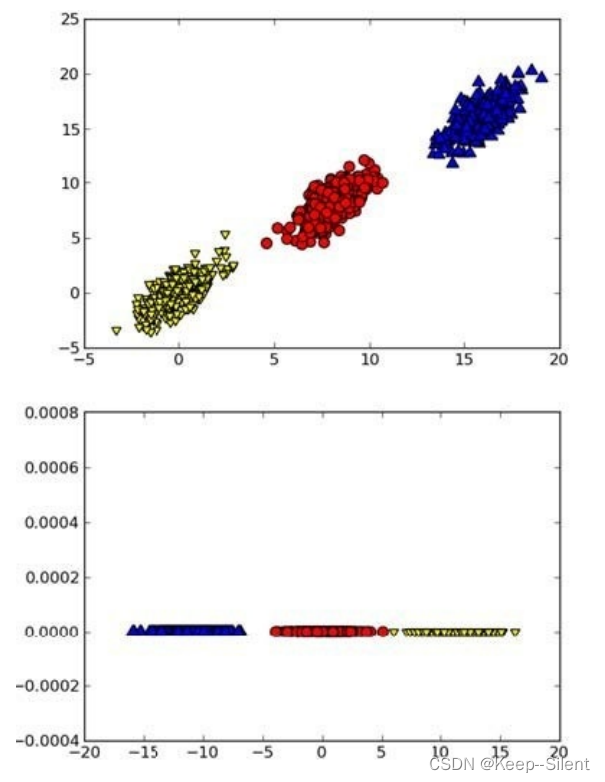
考察下图,其中的数据来⾃于上⾯的图并经PCA转换之后绘制⽽成的。如果仅使⽤原始数据,那么这⾥的间隔会⽐决策树的间隔更⼤。另外,由于只需要考虑⼀维信息,因此数据就可以通过⽐SVM简单得多的很容易采⽤的规则进⾏区分。
13.2.2在NumPy中实现PCA
加载数据集
from numpy import *
import numpy as npdef loadDataSet(fileName, delim='\t'):fr = open(fileName)stringArr = [line.strip().split(delim) for line in fr.readlines()]datArr = [list(map(float, line)) for line in stringArr]return mat(datArr)
dataMat = loadDataSet('13testSet.txt')
dataMat
matrix([[10.235186, 11.321997],[10.122339, 11.810993],[ 9.190236, 8.904943],...,[ 9.854922, 9.201393],[ 9.11458 , 9.134215],[10.334899, 8.543604]])
PCA过程:
- 去除平均值
- 计算协方差矩阵
- 计算协方差矩阵的特征值和特征向量
- 将特征值从大到小排序
- 保留最上⾯的N个特征向量
- 将数据转换到上述N个特征向量构建的新空间中
def pca(datMat, topNfeat=9999999):meanVals = datMat.mean(0)meanRemoved = datMat - meanVals # 1. 去除平均值covMat = cov(meanRemoved, rowvar=0) # 2. 计算协⽅差矩阵eigVals, eigVects = linalg.eig(mat(covMat)) # 3. 计算协⽅差矩阵的特征值和特征向量eigValInd = argsort(eigVals) # 4. 将特征值从⼤到⼩排序eigValInd = eigValInd[:-(topNfeat+1):-1] # 保留topNfeat个维度redEigVects = eigVects[:, eigValInd] # 5. 保留最上⾯的N个特征向量lowDDataMat = meanRemoved * redEigVects # 6. 将数据转换到上述N个特征向量构建的新空间中reconMat = (lowDDataMat * redEigVects.T) + meanValsreturn lowDDataMat, reconMat
显示部分PCA数据
lowDMat, reconMat = pca(dataMat, 1)
print('lowDMat',lowDMat[:3,:])
print('reconMat',reconMat[:3,:])
lowDMat [[-2.51033597][-2.86915379][ 0.09741085]]
reconMat [[10.37044569 11.23955536][10.55719313 11.54594665][ 9.01323877 9.01282393]]
进行数据可视化:
- 展示原始所有数据dataMat
- 绘制第一坐标轴reconMat
import matplotlib
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(dataMat[:, 0].flatten().A[0], dataMat[:, 1].flatten().A[0], marker='^', s=90)
ax.scatter(reconMat[:, 0].flatten().A[0], reconMat[:, 1].flatten().A[0], marker='o', s=50, c='red')plt.show()

13.3利用PCA对半导体制造数据降维
dataMat = loadDataSet('13secom.data',' ')
print(shape(dataMat))
print(dataMat[20:24,:4])
(1567, 590)
[[2987.32 2528.81 nan nan][ nan 2481.85 2207.3889 962.5317][3002.27 2497.45 2207.3889 962.5317][2884.74 2514.54 2160.3667 899.9488]]
可以看出数据量1567,和数据维度590
其中,数据中有NaN数据需要处理,接下来处理NaN数据
def replaceNanWithMean(dataMat): numFeat = shape(dataMat)[1]for i in range(numFeat):meanVal = mean(dataMat[nonzero(~isnan(dataMat[:,i].A))[0],i]) #values that are not NaN (a number)dataMat[nonzero(isnan(dataMat[:,i].A))[0],i] = meanVal #set NaN values to meanreturn dataMat
dataMat=replaceNanWithMean(dataMat)
print(dataMat[20:24,:4])
[[2987.32 2528.81 2200.54731771 1396.37662737][3014.45289558 2481.85 2207.3889 962.5317 ][3002.27 2497.45 2207.3889 962.5317 ][2884.74 2514.54 2160.3667 899.9488 ]]
可以看到NaN已经处理为了平均值
计算特征值
meanVals = dataMat.mean(0)
meanRemoved = dataMat - meanVals # 1. 去除平均值
covMat = cov(meanRemoved, rowvar=0) # 2. 计算协⽅差矩阵
eigVals, eigVects = linalg.eig(mat(covMat)) # 3. 计算协⽅差矩阵的特征值和特征向量
eigVals = sort(eigVals) # 4. 将特征值从⼤到⼩排序
print(eigVals)
[-1.77898285e-16 -6.91541208e-19 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 0.00000000e+00 0.00000000e+000.00000000e+00 0.00000000e+00 6.06554565e-18 9.84684997e-164.76825507e-15 1.80003664e-10 1.97062976e-10 2.61901629e-105.27591520e-10 6.13351286e-10 6.95078509e-10 9.24977925e-10
...1.25591691e+03 1.33096008e+03 1.53948465e+03 1.66199683e+031.70492093e+03 1.76741826e+03 1.86414157e+03 2.16835314e+032.35027999e+03 2.74523635e+03 3.24193522e+03 3.41199406e+034.10673182e+03 4.23060022e+03 4.95614671e+03 5.34196392e+037.22765535e+03 8.34665462e+03 9.48876548e+03 1.04841308e+041.09321187e+04 1.44089194e+04 1.47123429e+04 2.67385181e+043.31436743e+04 3.55294040e+04 4.15532551e+04 4.41914029e+044.54661746e+04 5.03324580e+04 5.16269933e+04 5.96776503e+046.52620058e+04 6.66060410e+04 7.76560524e+04 8.15850591e+048.33473762e+04 1.00166164e+05 1.02849533e+05 1.08493848e+051.13215032e+05 1.52422354e+05 1.86856549e+05 1.96098849e+052.08513836e+05 2.37155830e+05 2.83668601e+05 2.90863555e+054.67693557e+05 1.31540439e+06 2.07388086e+06 8.24837662e+062.17466719e+07 5.34151979e+07]
其中有大量特征值都是0。这就意味着这些特征都是其他特征的副本,也就是说,它们可以通过其他特征来表示,而本身并没有提供额外的信息
我们可以尝试不同的截断值来检验它们的性能。有些人使用能包含90%信息量的主成分数量,而其他人使用前20个主成分。我们无法精确知道所需要的主成分数目,必须通过在实验中取不同的值来确定。有效的主成分数目则取决于数据集和具体应用。
上述分析能够得到所用到的主成分数目,然后我们可以将该数目输入到PCA算法中(如lowDMat, reconMat = pca(dataMat,20)),最后得到约简后数据就可以在分类器中使用了。
相关文章:

第十三章 利用PCA简化数据
文章目录 第十三章 利用PCA简化数据13.1降维技术13.2PCA13.2.1移动坐标轴 13.2.2在NumPy中实现PCA13.3利用PCA对半导体制造数据降维 第十三章 利用PCA简化数据 PCA(Principal Component Analysis,主成分分析)是一种常用的降维技术࿰…...

开源中文分词Ansj的简单使用
ANSJ是由孙健(ansjsun)开源的一个中文分词器,为ICTLAS的Java版本,也采用了Bigram HMM分词模型:在Bigram分词的基础上,识别未登录词,以提高分词准确度。 虽然基本分词原理与ICTLAS的一样&#…...

251_多线程_创建一个多线程的图像处理应用,其中每个线程负责对一部分图像进行处理,然后将处理后的结果合并为最终图像
举一个更丰富的例子来说明多线程的用法。 我们将创建一个多线程的图像处理应用,其中每个线程负责对一部分图像进行处理,然后将处理后的结果合并为最终图像。 这个例子可以更好地展示多线程并发处理的优势。 假设有一个函数 processImageSection,它会对图像的一个特定区域进…...

[吐槽Edge浏览器]关于Edge浏览器的闪退问题
这个浏览器嘛,在谷歌浏览器不能页面翻译后,一直是用的高高兴兴的,可突然有一天,Edge浏览器页面加载不出来了。 很慌,大概就是页面崩溃、加载失败什么的都出现过。 修了整整一天,不知道原因在哪,…...

数据包在网络中传输的过程
ref: 【先把这个视频看完了】:数据包的传输过程【网络常识10】_哔哩哔哩_bilibili 常识都看看 》Ref: 1. 这个写的嘎嘎好,解释了为啥4层7层5层,还有数据包封装的问题:数据包在网络中的传输过程详解_数据包传输_张孟浩_jay的博客…...

Acwing.875 快速幂
题目 给定n组ai , bi, pi,对于每组数据,求出akimod pi的值。 输入格式 第一行包含整数n。 接下来n行,每行包含三个整数ai , bi,pi。输出格式 对于每组数据,输出一个结果,表示aibimod pi的值。 每个结果占一行。 数…...
【决策树-鸢尾花分类】
决策树算法简介 决策树是一种基于树状结构的分类与回归算法。它通过对数据集进行递归分割,将样本划分为多个类别或者回归值。决策树算法的核心思想是通过构建树来对数据进行划分,从而实现对未知样本的预测。 决策树的构建过程 决策树的构建过程包括以…...
)
类与对象(中--构造函数)
类与对象(中--构造函数) 1、构造函数的特性2、默认构造函数3、编译器自动生成的默认构造函数(无参的)(当我们不写构造函数时)3.1 编译器自动生成的默认构造函数只对 自定义类型的成员变量 起作用࿰…...

Makefile学习1
文章目录 Makefile学习1Makefile简介Makefile重要性Makefile内容1) 显式规则2) 隐晦规则3) 变量的定义4) 文件指示5) 注释 Makefile规则规则默认目标多目标多规则目标伪目标 Makefile目标依赖头文件依赖自动生成头文件依赖关系 Makefile命令Makefile变量变量定义和使用赋值立即…...
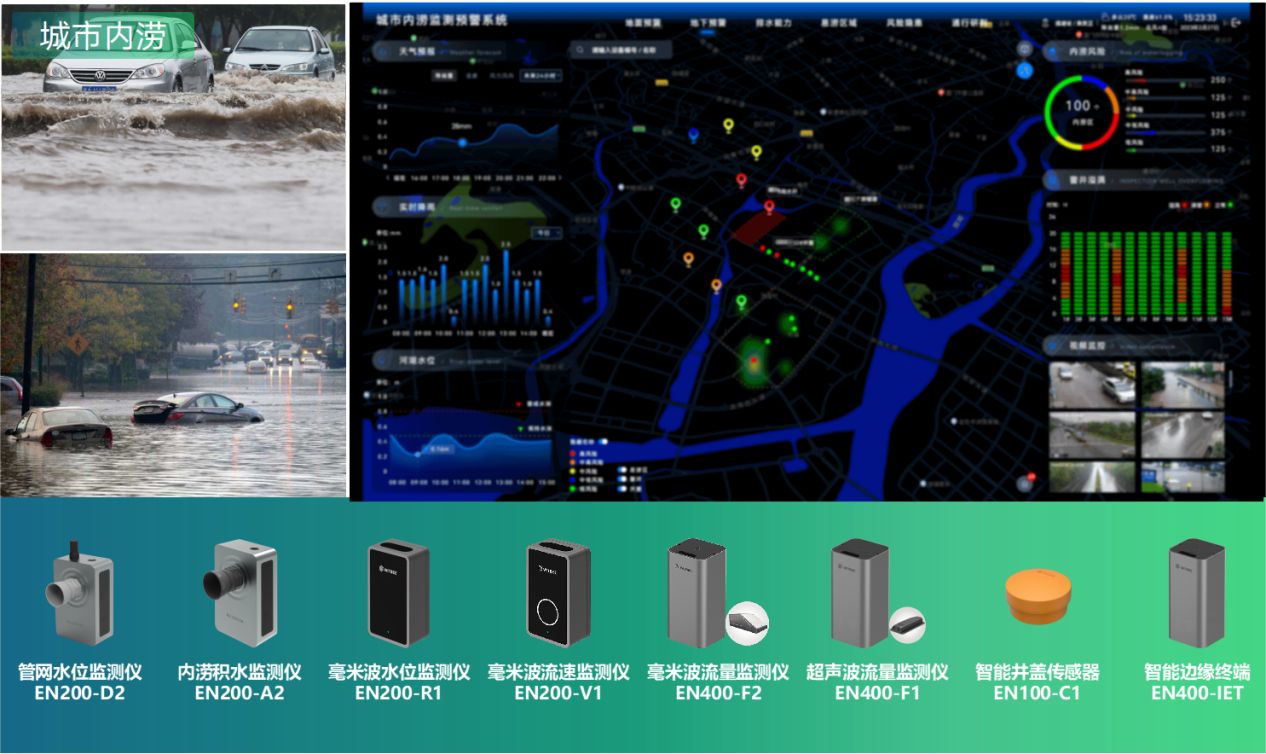
城市内涝监测预警系统,科学“智治”应对灾害
近日,台风“杜苏芮”以摧枯拉朽之势给我国东南沿海地区带来狂风骤雨,福建的三个国家气象观测站日降水量突破历史极值。之后,“杜苏芮”一路北上。中央气象台预报称,7月29日至8月1日,北京、天津、河北、山东西部、河南北…...

切片[::-1]解析列表list表示的“非负整数加1”
列表数位表示非负整数,熟练操作“满十进位”。 (本笔记适合熟练操作Python列表list的 coder 翻阅) 【学习的细节是欢悦的历程】 Python 官网:https://www.python.org/ Free:大咖免费“圣经”教程《 python 完全自学教程》,不仅仅…...
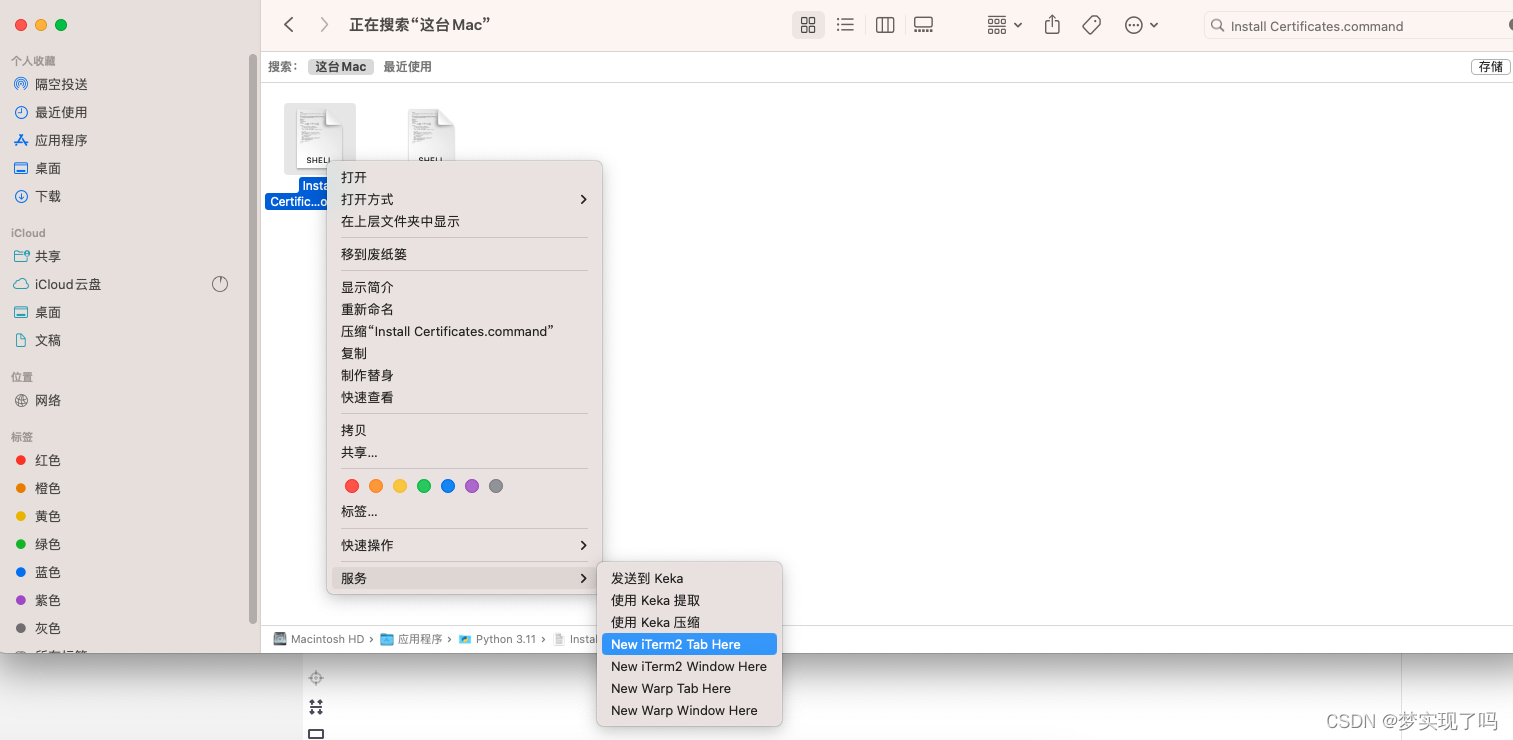
Mac下certificate verify failed: unable to get local issuer certificate
出现这个问题,可以安装证书 在finder中查找 Install Certificates.command找到后双击,或者使用其他终端打开 安装完即可...

Django项目启动错误
uwsgi项目启动错误信息如下Did you install mysqlclient?Command pkg-config --exists mysqlclient returned non-zero exit status 1Command pkg-config --exists mariadb returned non-zero exit status 1.Traceback (most recent call last):File "/home/dream21th/co…...

Vue2 第十二节 Vue组件化编程 (二)
1. VueComponent 2. 单文件组件 一. VueComponent 组件本质上是一个名为VueComponent的构造函数,不是程序员定义的,是Vue.extend生成的只需要写<school/>或者<school><school/>,Vue解析时,会帮我们创建schoo…...
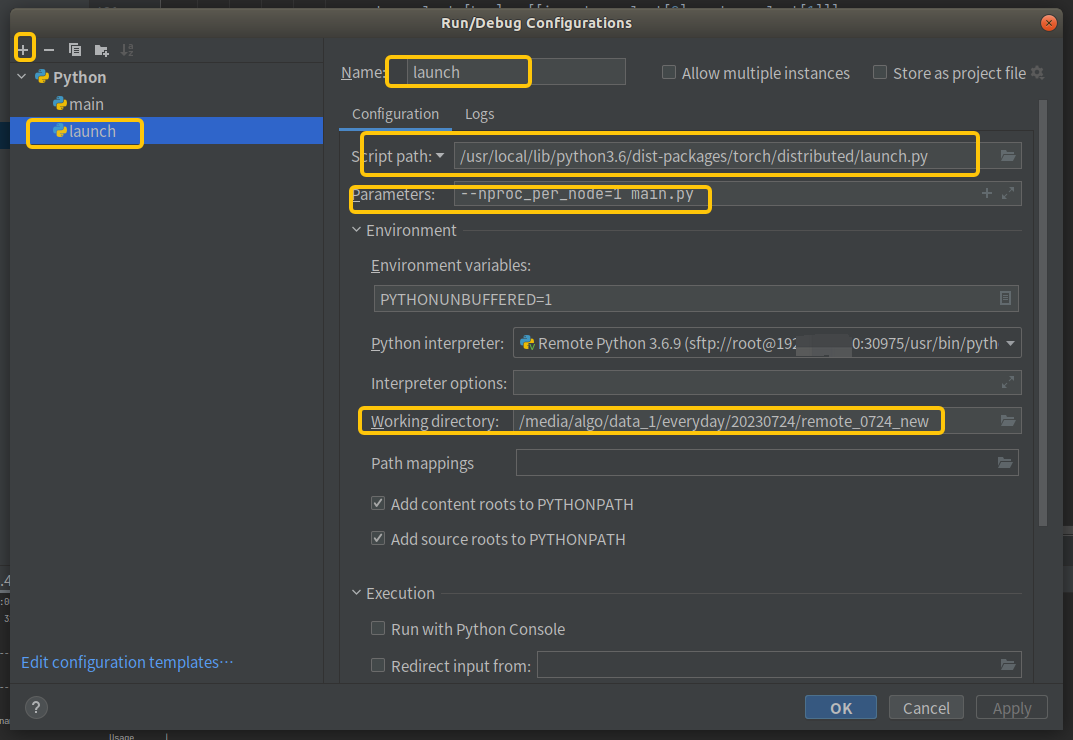
pycharm 远程连接服务器并且debug, 支持torch.distributed.launch debug
未经允许,本文不得转载,vx:837007389 文章目录 step1:下载专业版本的pycharmstep2 配置自动同步文件夹,即远程的工程文件和本地同步2.1 Tools -> Deployment -> configuration2.2 设置同步文件夹2.3 同步服务器…...

SAP ABAP 基础语法超详细
1.表声明 Tables: 表名[,表名]. 声明多个表时可用逗号分隔当你声明了一个数据表的同时,系统也同时自动生成了一个和数据表同名的结构,结构的变量集等于数据表里面的字段。 2.定义变量 Data: v1[(l)] [type t] [decimals d] [v…...

html学习3(表格table、列表list)
1、html表格由<table>标签来定义。 <thead>用来定义表格的标题部分,其内部用 <th > 元素定义列的标题,可以使其在表格中以粗体显示,与普通单元格区分开来。<tbody>用来定义表格的主体部分,其内部用<t…...

【SpringBoot】85、SpringBoot中Boolean类型数据转0/1返回序列化配置
在 SpringBoot 中,前端传参数 0,1,后端可自动解析为 boolean 类型,但后端返回前端 boolean 类型时,却无法自动转换为 0,1,所以我们需要自定义序列化配置,将 boolean 类型转化为 0,1 1、类型对应 boolean 类型有false,true对应的 int 类型0,12、序列化配置 import com.f…...

hbase优化:客户端、服务端、hdfs
hbase优化 一.读优化 1.客户端: scan。cache 设置是否合理:大scan场景下将scan缓存从100增大到500或者1000,用以减少RPC次数使用批量get进行读取请求离线批量读取请求设置禁用缓存,scan.setBlockCache(false)以指定列族或者列进行…...

docker安装memcached
查找容器是否有该镜像存在 docker search memcached拉取镜像 docker pull memcached创建容器 docker create --name memcache1 memcached或者映射一下端口 docker create -p 11211:11211 --name memcache1 memcached启动 docker start memcache1指定容器的 IP docker net…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...

Vue.js教学第二十一章:vue实战项目二,个人博客搭建
基于 Vue 的个人博客网站搭建 摘要: 随着前端技术的不断发展,Vue 作为一种轻量级、高效的前端框架,为个人博客网站的搭建提供了极大的便利。本文详细介绍了基于 Vue 搭建个人博客网站的全过程,包括项目背景、技术选型、项目架构设计、功能模块实现、性能优化与测试等方面。…...

简约商务年终工作总结报告PPT模版分享
简约精致扁平化商务通用动画PPT模版,简约大气素雅商务PPT模版,商务PPT模版,商业计划书PPT模版,IOS风商务通用PPT模版,公司介绍企业宣传PPT模版,创业融资PPT模版,创意低多边形PPT模版,…...
