二叉树(C语言)
文章目录
- 1.树
- 1.1概念
- 1.2相关定义
- 1.3 表示(左孩子右兄弟)
- 2.二叉树
- 2.1概念
- 2.2特殊的二叉树
- 1. 满二叉树:
- 2. 完全二叉树:
- 2.3二叉树的性质
- 2.4练习
- 3.二叉树的存储结构
- 1. 顺序存储
- 2. 链式存储
- 4.完全二叉树的代码实现
- 4.1堆的介绍
- 1.堆的性质:
- 2.堆的应用
- 4.2堆的实现
- 1.Heap.h
- 2.Heap.c
- 3.test.c
- 4.3堆的应用
- 1.堆排序
- 1.1建堆时间复杂度(最优为下调N)
- 1.1.1下调O(N)
- 1.1.2 上调O(NlogN)
- 1.2代码实现
- 1.3堆排序时间复杂度
- 2.topk问题
- 2.1介绍及解决方式
- 2.2代码举例
- 5.普通二叉树的结构
- 5.1代码实现
- 5.2算法图解(递归)
1.树
1.1概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i
<= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继 - 树是递归定义的。
- 树形结构中,子树之间不能有交集,否则就不是树形结构
1.2相关定义
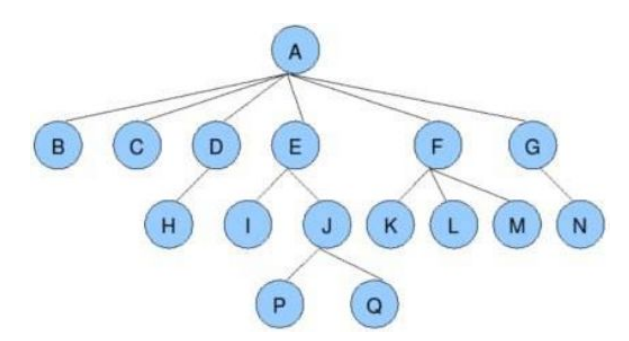
- 节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
- 叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点
- 非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
- 树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m(m>0)棵互不相交的树的集合称为森林;
1.3 表示(左孩子右兄弟)

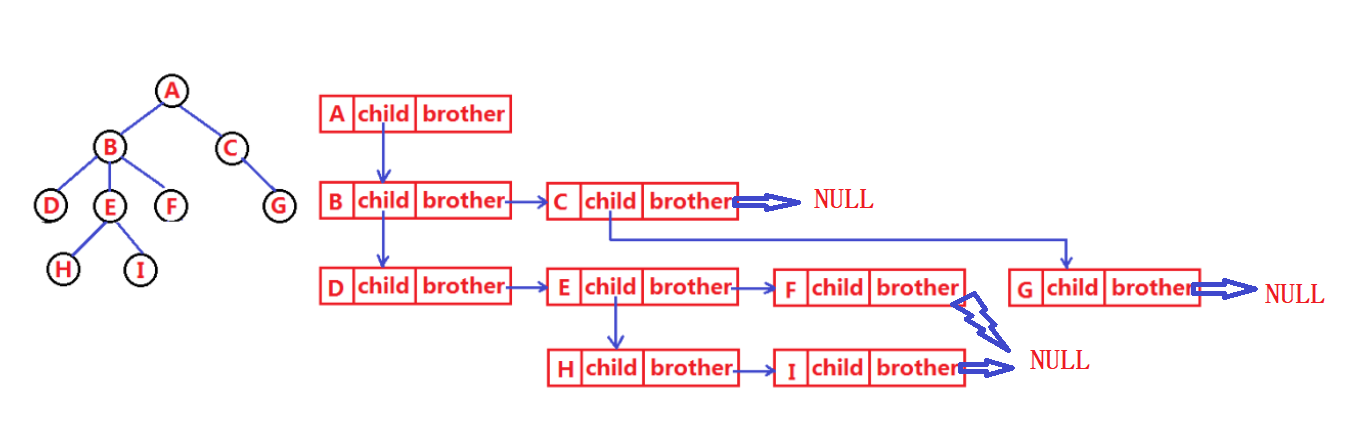
2.二叉树
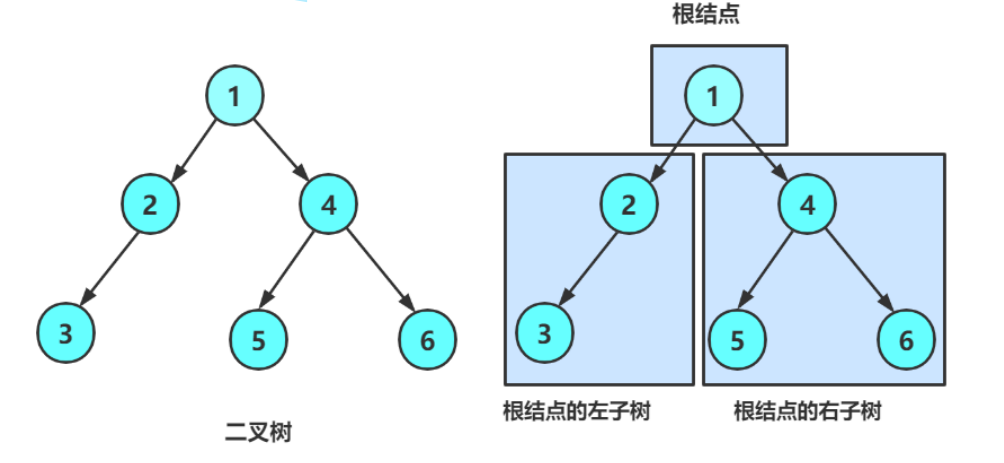
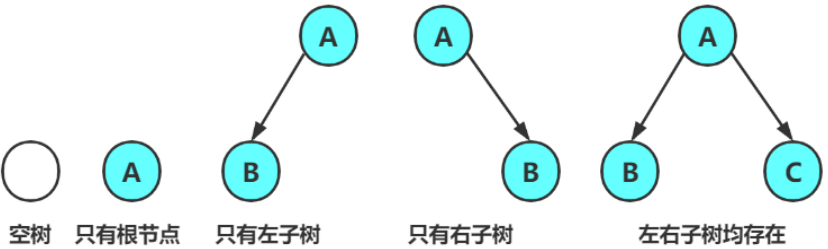
2.1概念
一棵二叉树是结点的一个有限集合,该集合:
- 可以为空
- 由一个根节点加上两棵称为左子树和右子树的二叉树组成
- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
2.2特殊的二叉树
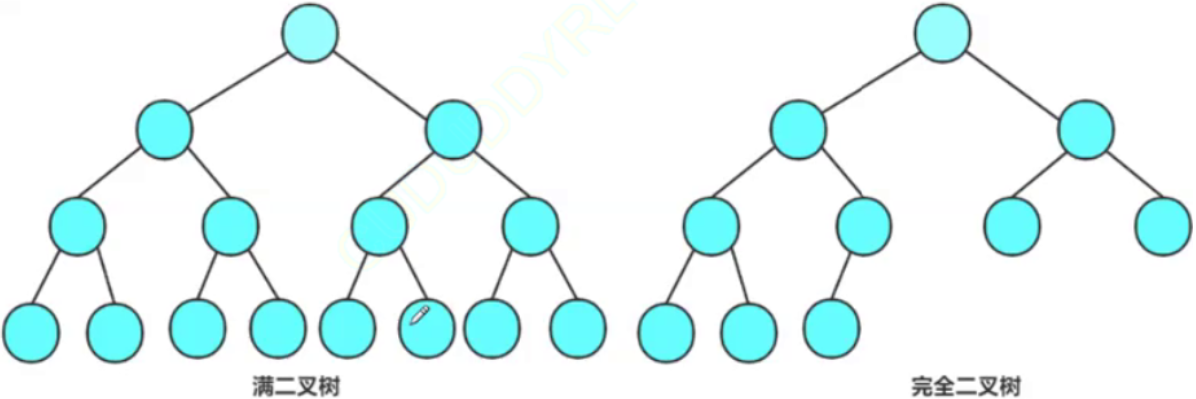
1. 满二叉树:
每一个层的结点数都达到了最大值的二叉树。
如果一个二叉树的层数为K,且结点总数是 2^k-1 ,则它就是满二叉树。
2. 完全二叉树:
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树引出来的。
对于深度为K结点为n的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对
应时称之为完全二叉树。
前k-1层是满二叉树 ; 第k层不满且从左到右连续 ; 若第k层也满 则为满二叉树
满二叉树是一种特殊的完全二叉树。
2.3二叉树的性质
若规定根节点的层数为1
- 一棵非空二叉树的第i层上最多有 2^(i - 1) 个结点
- 深度为k的二叉树的最大结点数(即满二叉树)是 2^k - 1
- 对任何一棵二叉树, 度为0的叶结点个数为x0 , 度为2的分支结点个数为 x2,则x0 = x2+1(度为0的永远比度为2的多1个)
- 具有n个结点的满二叉树的深度,h=log2(n+1)
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对
于序号为i的结点有:
i=0,i为根节点编号,无双亲节点
i>0,i的父节点:(i-1)/22i+1<n,左孩子序号:2i+1(2i+1>=n无左孩子)
2i+2<n,右孩子序号:2i+2(2i+2>=n无右孩子)
- 高度为h的完全二叉树的结点个数区间:【2^(h-1) ,2^h-1】
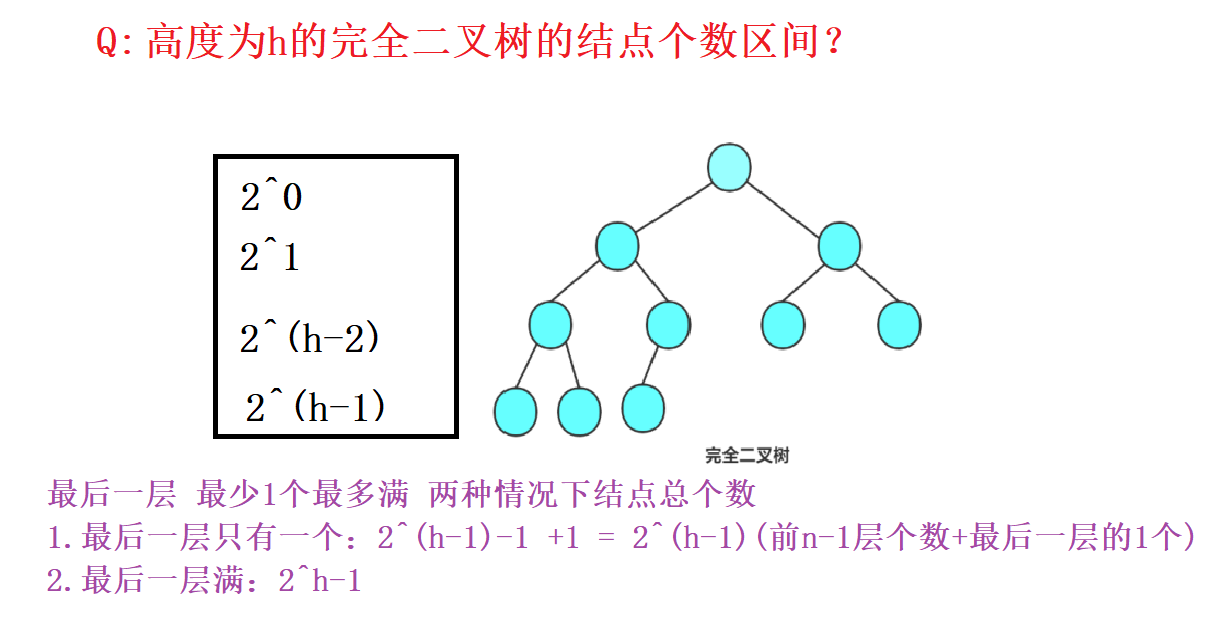
2.4练习
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( 200 )
A 不存在这样的二叉树
B 200
C 198
D 199
x0 = x2+1
2.下列数据结构中,不适合采用顺序存储结构的是( A )
A 非完全二叉树
B 堆
C 队列
D 栈
3.在具有 2n 个结点的完全二叉树中,叶子结点个数(即x0)为( A )
A n
B n+1
C n-1
D n/2
完全二叉树:前k-1层是满二叉树 ; 第k层不满且从左到右连续
2n = x0 + x1 + x2
2n = x0 + x1 + x0 - 1
2n = 2x0 + x1 - 1
x1为0/1 2n为整数 x1只能为1 ==》x0 = n
4.一棵完全二叉树的节点数为531个,那么这棵树的高度为( B )
A 11
B 10
C 8
D 12
法一:如果是满二叉树 h = 256 512 10242^ 8 9 10
法二:利用结论【2^(h-1) ,2^h-1】
5.一个具有767个节点的完全二叉树,其叶子节点个数为( B )
A 383
B 384
C 385
D 386
完全二叉树:前k-1层是满二叉树 ; 第k层不满且从左到右连续
767 = x0 + x1 + x2
767 = x0 + x1 + x0 - 1
767 = 2x0 + x1 - 1
x1为0/1 767为奇数 x1只能为0 ==》x0 = 384
3.二叉树的存储结构
1. 顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,不是完全二叉树会有空
间浪费。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。通常把堆(一种二叉树)用顺序结构的数组来存储,这里的堆是数据结构,操作系统虚拟进程地址空间中的堆是管理内存的一块区域分段。
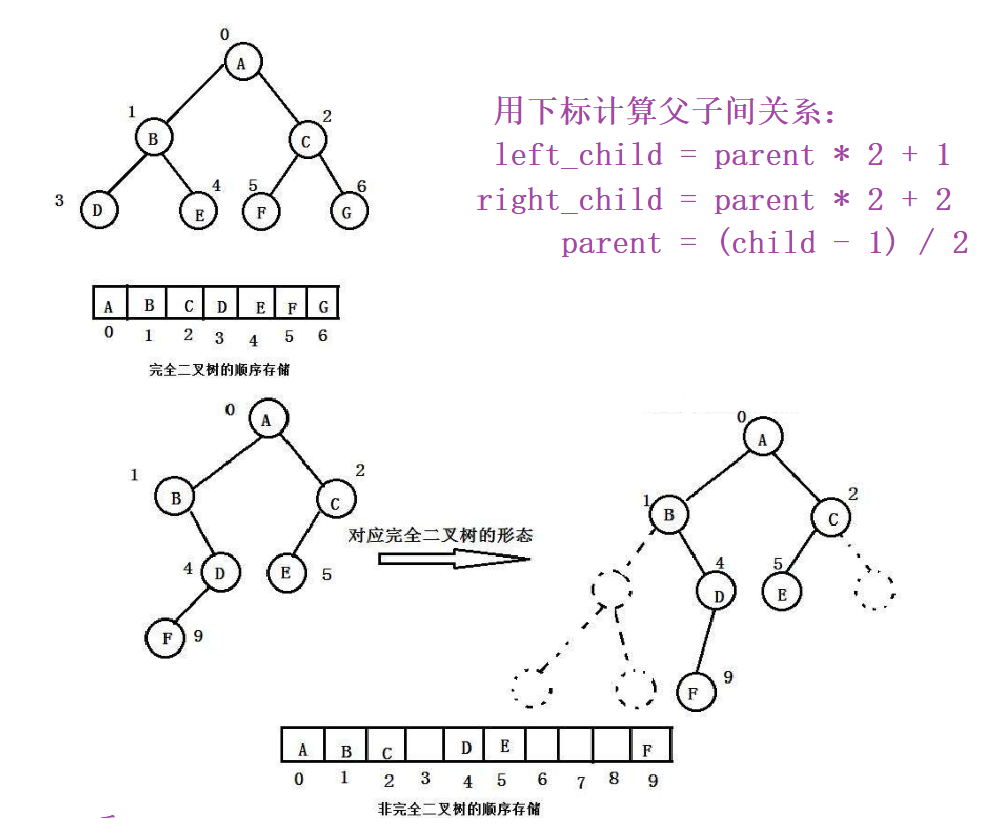
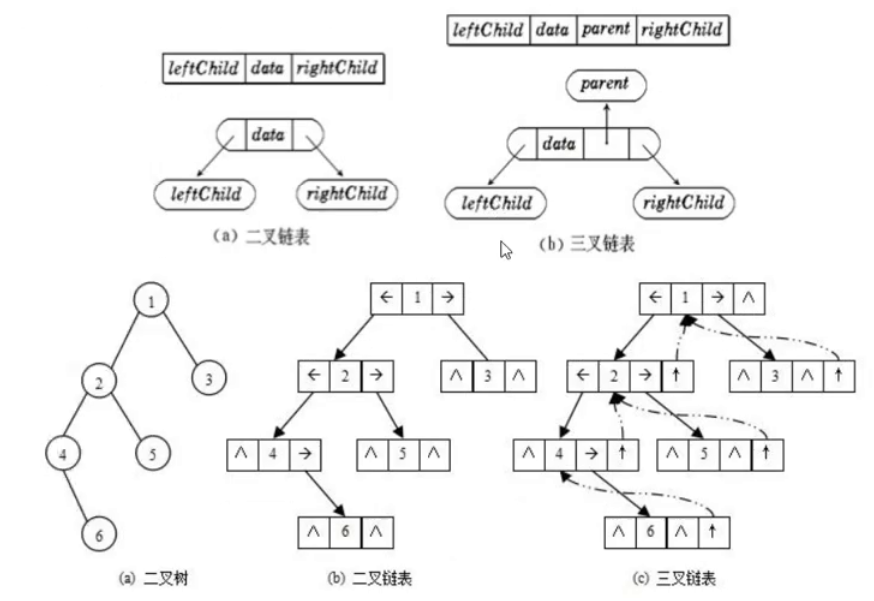
2. 链式存储
链式存储结构是用链表来表示一棵二叉树,即用链表来指示元素的逻辑关系。 链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在链结点的存储地址 。链式结构分为二叉链和三叉链。
4.完全二叉树的代码实现
4.1堆的介绍
如果有一个关键码的集合K = { , , ,…, },把它的所有元素按完全二叉树的顺序存储方式存储
在一个一维数组中,并满足: <= 且 <= ( >= 且 >= ) i = 0,1,
2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
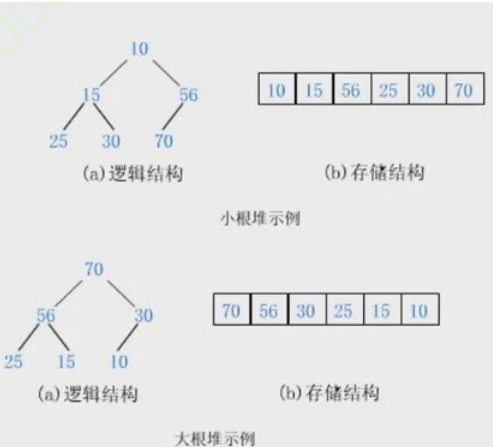
1.堆的性质:
- 堆中某个节点的值总是>= 或 <=其父节点的值;
- 小根堆:子节点值>=父亲
- 大根堆:子节点值<=父亲
- 堆总是一棵完全二叉树。
2.堆的应用
1.堆排序: – O(N * logN)
2.topk问题
4.2堆的实现
1.Heap.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;//交换
void Swap(HPDataType* p1, HPDataType* p2);//打印
void HeapPrint(HP* php);//上调
void AdjustUp(HPDataType* a, int child);//下调
void AdjustDwon(HPDataType* a, int size, int parent);//初始化
void HeapInit(HP* php);//销毁
void HeapDestroy(HP* php);//入堆
void HeapPush(HP* php, HPDataType x);//出堆
void HeapPop(HP* php);//判空
bool HeapEmpty(HP* php);//取堆头
HPDataType HeapTop(HP* php);//堆大小
int HeapSize(HP* php);2.Heap.c
#include "Heap.h"//交换
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}//打印
void HeapPrint(HP* php)
{assert(php);for (int i = 0; i < php->size; ++i){printf("%d ", php->a[i]);}printf("\n");
}//上调logN
void AdjustUp(HPDataType* a, int child)
{//定位父节点下标int parent = (child - 1) / 2;while (child > 0){// if (a[child] > a[parent]) //大堆if (a[child] < a[parent]) //小堆{//交换数据Swap(&a[child], &a[parent]);//交换后更新child = parent;parent = (child - 1) / 2;}else{break;}}
}//下调logN
void AdjustDwon(HPDataType* a, int size, int parent)
{//设左孩子较小int child = parent * 2 + 1;//当未达到堆末 进入循环while (child < size){//确定real大孩子// if (child + 1 < size && a[child + 1] > a[child]) //大堆//确定real小孩子if (child + 1 < size && a[child + 1] < a[child]) //小堆{++child;}// if (a[parent] > a[child]) //大堆if (a[parent] > a[child]) //小堆{Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}//销毁
void HeapDestroy(HP* php)
{assert(php); free(php->a);php->a = NULL;php->size = php->capacity = 0;
}//入堆
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){printf("realloc fail\n");exit(-1);}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;//上调 插入的新数据的下标AdjustUp(php->a, php->size - 1);
}//出堆
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);//想要删除堆头 把堆头与堆末交换Swap(&(php->a[0]), &(php->a[php->size - 1]));//删除堆末 -- 原目标值(堆头)已被删除php->size--;//将原堆末(现堆头下调置适当位置)AdjustDwon(php->a, php->size, 0);
}//取堆头
HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}//判空
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}//堆大小
int HeapSize(HP* php)
{assert(php);return php->size;
}3.test.c
#define _CRT_SECURE_NO_WARNINGS
#include"Heap.h"//测试函数
void TestHeap()
{//创建HP hp;//初始化HeapInit(&hp);//入堆int a[] = { 27, 15, 19, 18, 28, 34, 65, 49, 25, 37 };for (int i = 0; i < sizeof(a) / sizeof(int); ++i){HeapPush(&hp, a[i]);}///打印HeapPrint(&hp);//入堆 -- 打印HeapPush(&hp, 10);HeapPrint(&hp);//出堆 -- 打印HeapPop(&hp);HeapPrint(&hp); HeapPop(&hp);HeapPrint(&hp);
}
4.3堆的应用
1.堆排序
1.1建堆时间复杂度(最优为下调N)
1.1.1下调O(N)
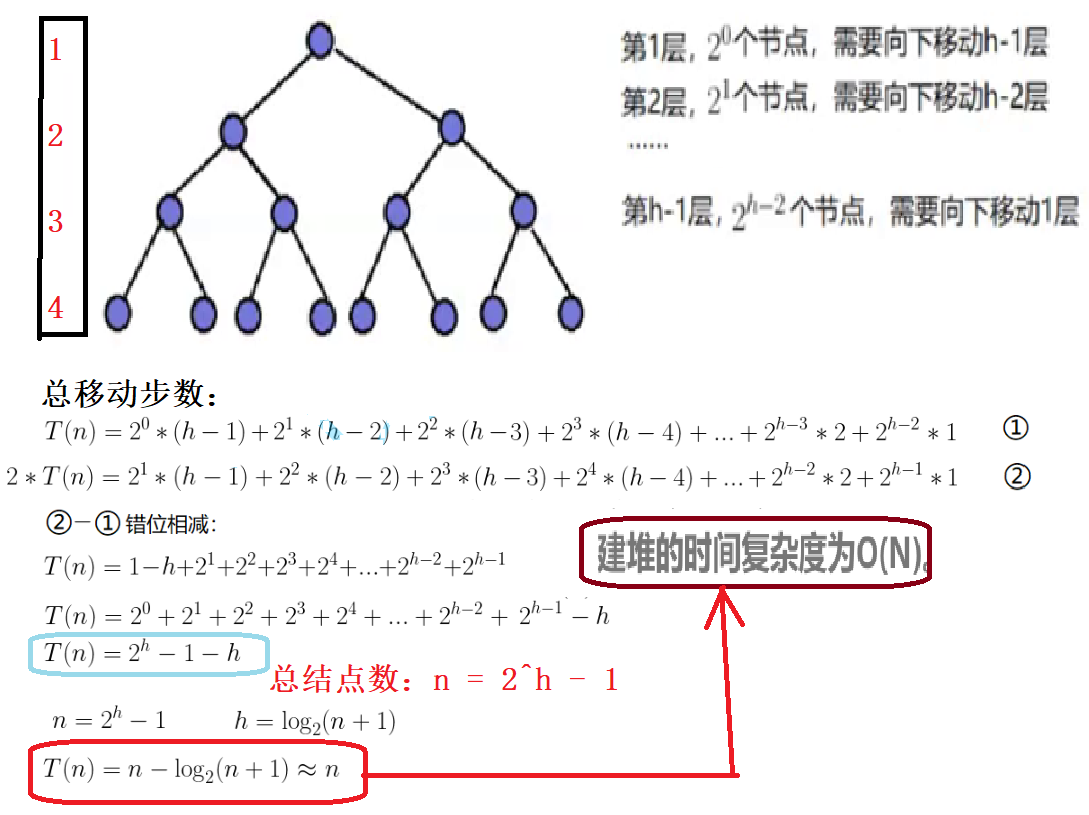
1.1.2 上调O(NlogN)
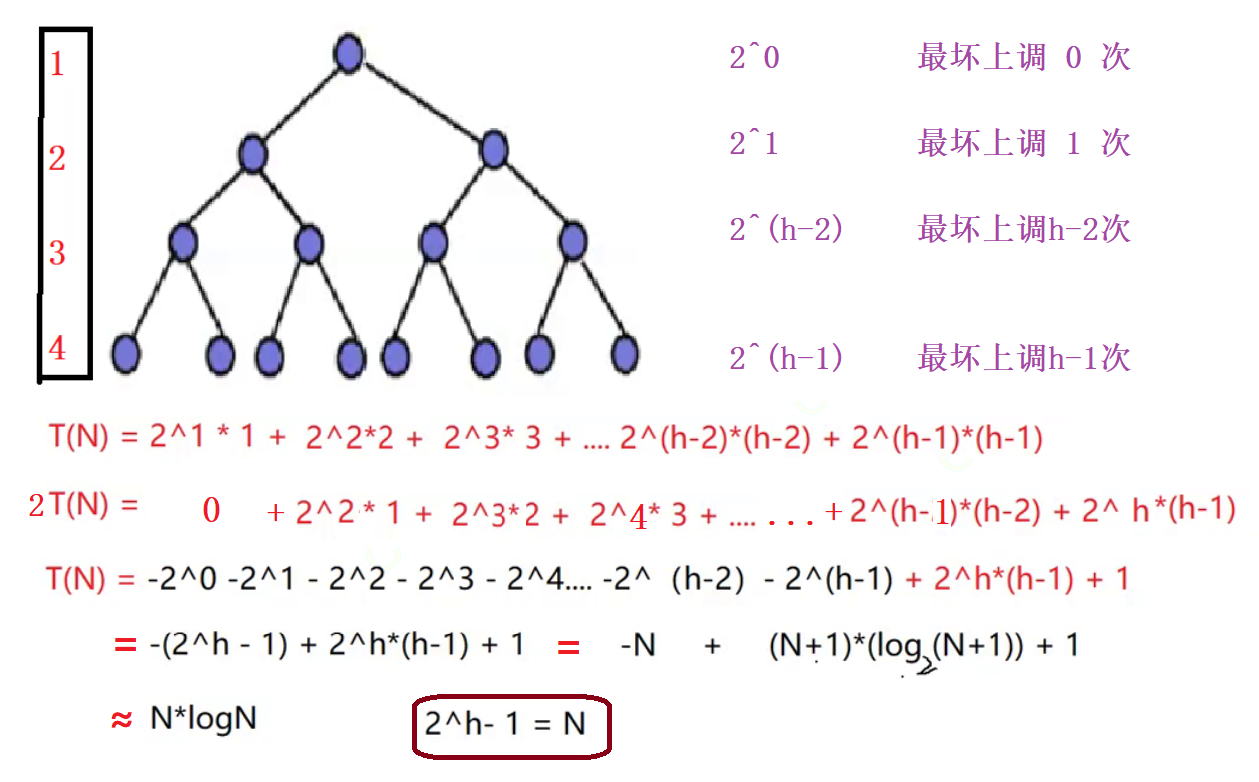
1.2代码实现
//堆排序1.0 升序<-->用<-->小堆 降序<-->用<-->大堆
//问题:
//1、需要有一个堆数据结构存在 才能创建堆对象
//2、在堆对象空间再创建一个数组 调整后回写 空间复杂度为 O(N)
void Low_HeapSort(int* a, int n)
{HP hp;HeapInit(&hp);for (int i = 0; i < n; ++i){HeapPush(&hp, a[i]);}int i = 0;while (!HeapEmpty(&hp)){a[i++] = HeapTop(&hp);HeapPop(&hp);}HeapDestroy(&hp);
}
//堆排序2.0 升序<-->建<-->大堆 降序<-->建<-->大堆
void Plus_HeapSort(int* a, int n)
{
//一、建堆
// 1.0 上调建堆法 O(N*logN)
// 将数组a传参后 假设原数组就是一颗树 只不过这棵树待调整
// 上调法:遍历数组 从1到n-1 上调至合适位置
// 定位父节点下标 int parent = (child - 1) / 2 --> i从1开始而非0/*for (int i = 1; i < n; ++i){AdjustUp(a, i);}*/
// 2.0 下调建堆法 O(N)
// 将数组a传参后 假设原数组就是一颗树 只不过这棵树待调整
// 下调法:遍历数组 叶子节点无孩子不用下调
// 从倒数第一个非叶子节点开始遍历至根节点
// 倒数第一个非叶子节点:末节点的父亲
// 公式计算父节点下标 int parent = (child - 1) / 2
// 末节点下标:n - 1 - 1
// 设左孩子较小 int child = parent * 2 + 1;for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDwon(a, n, i);}
//二、排序(升序法:将大值一次排到尾部 建大堆-->根最大) O(N*logN)//定位末节点int end = n - 1;//排序 遍历已经调好位置的大堆while (end > 0){//头尾交换(最大的值(根结点)与末节点的值交换)//下调Swap(&a[0], &a[end]);AdjustDwon(a, end, 0);//下标前移--end;}
}//测试堆排序
void TestHeapSort()
{int a[] = { 27, 15, 19, 18, 28, 34, 65, 49, 25, 37 };Plus_HeapSort(a, sizeof(a) / sizeof(int));for (int i = 0; i < sizeof(a) / sizeof(int); i++){printf("%d ", a[i]);}
}int main()
{TestHeapSort();return 0;
}
1.3堆排序时间复杂度
堆排序时间复杂度 = 建堆 + 排序
= O(N) + O(N*longN)
= O(NlogN)
2.topk问题
2.1介绍及解决方式
介绍:
求数据结合中前K个最大的元素或者最小的元素
解决方式:
用堆来解决 基本思路:
- 思路一:O(N * logN)
将N个数据进行排序 目前接触到的排序算法最优为堆排序 - 思路二:O(N + k * logN) 【N个数据建堆空间浪费巨大】
将N个数据建成大堆 然后Top/Pop k次 时间复杂度 = 下调建大堆 + Top/Pop - 思路三:O[K + (N-K) * logK] 【最优 时间上可能比二差点 但空间上效率提高】
将N个数据前K个元素建堆:取前k个最大的元素–建小堆;取前k个最小的元素,建大堆
用剩余的N-K个元素依次与堆顶元素比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

2.2代码举例
//打印Topk函数
void PrintTopK(int* a, int n, int k)
{// 1.下调建堆 -- 用前k个元素建堆//申请空间int* kHeap = (int*)malloc(sizeof(int) * k);assert(kHeap);//拷贝前k个for (int i = 0; i < k; ++i){kHeap[i] = a[i];}//显示kHeapprintf("kHeap的数据显示\n");for (int i = 0; i < k; ++i){printf("%d ", kHeap[i]);}printf("\n");//下调建堆for (int i = (k - 1 - 1) / 2; i >= 0; --i){AdjustDwon(kHeap, k, i); //此时AdjustDwon实现的是建小堆} //显示kHeapprintf("kHeap的数据显示\n");for (int i = 0; i < k; ++i){printf("%d ", kHeap[i]);}printf("\n");// 2.访问数组a中n-k个元素 -- 依次与堆顶元素比较 -- 不满足则替换for (int j = k; j < n; ++j){if (a[j] > kHeap[0]){kHeap[0] = a[j];AdjustDwon(kHeap, k, 0);printf("kHeap的数据显示\n");for (int i = 0; i < k; ++i){printf("%d ", kHeap[i]);}printf("\n");}}//打印printf("kHeap的数据显示\n");for (int i = 0; i < k; ++i){printf("%d ", kHeap[i]);}printf("\n");
}//Topk测试函数
void TestTopk()
{//一、生成10个<=100的数int* a = (int*)malloc(sizeof(int) * 10);srand(time(0));for (int i = 0; i < 10; ++i){a[i] = rand() % 100;}//将其中5个数修改成大于100的数a[6] = 100 + 6;a[4] = 100 + 9;a[8] = 100 + 2;a[2] = 100 + 1;a[0] = 100 + 4;//打印查看printf("a的数据显示\n");for (int i = 0; i < 10; ++i){printf("%d ", a[i]);}printf("\n");//检验PrintTopK(a, 10, 5);
}int main()
{TestTopk();return 0;
}
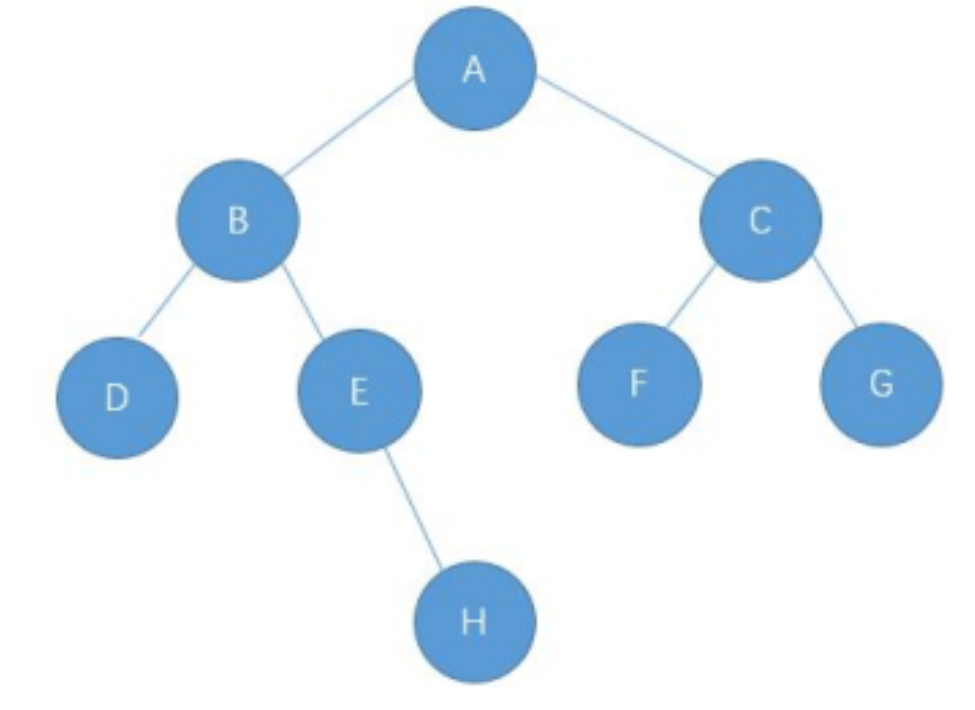
5.普通二叉树的结构
5.1代码实现
#define _CRT_SECURE_NO_WARNINGS#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>typedef int BTDataType;
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;BTDataType data;
}BTNode;//创建新结点
BTNode* CreatNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));assert(node);node->data = x;node->left = NULL;node->right = NULL;return node;
}//自创二叉树
BTNode* CreatBinaryTree()
{BTNode* node1 = CreatNode(1);BTNode* node2 = CreatNode(2);BTNode* node3 = CreatNode(3);BTNode* node4 = CreatNode(4);BTNode* node5 = CreatNode(5);BTNode* node6 = CreatNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}//前序遍历NLR
void PreOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}//中序遍历LNR
void InOrder(BTNode* root)
{if (root == NULL){printf("# ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}//后序遍历LRN
void PostOrder(BTNode* root)
{if (root == NULL) {printf("# ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}//结点个数1.0--NLR
int count = 0;
void TreeSize1(BTNode* root)
{if (root == NULL){return;}++count;TreeSize1(root->left);TreeSize1(root->right);
}//结点个数2.0--LRN
int TreeSize2(BTNode* root)
{return root == NULL ? 0 :TreeSize2(root->left) + TreeSize2(root->right) + 1;
}//叶子结点数--LRN
int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}//第k层结点个数--LRN
int TreeKLevel(BTNode* root, int k)
{assert(k >= 1);if (root == NULL)return 0;if (k == 1)return 1;return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}// 求二叉树深度--LRN
int TreeDepth(BTNode* root)
{if (root == NULL)return 0;int leftDepth = TreeDepth(root -> left);int rightDepth = TreeDepth(root -> right);return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}//查找目标结点--NLR
BTNode* TreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root; BTNode* ret1 = TreeFind(root->left, x); if (ret1) return ret1;BTNode* ret2 = TreeFind(root->right, x); if (ret2) return ret2;return NULL;
}int main()
{//创建二叉树 BTNode* root = CreatBinaryTree();//NLRPreOrder(root);printf("\n");//LNRInOrder(root);printf("\n");//LRNPostOrder(root);printf("\n");//结点个数1.0count = 0;TreeSize1(root);printf("TreeSize:%d\n", count);//结点个数2.0printf("TreeSize:%d\n", TreeSize2(root));printf("TreeSize:%d\n", TreeSize2(root));//叶子结点数printf("LeafSize:%d\n", TreeLeafSize(root));//第k层结点个数printf("KLevelSize:%d\n", TreeKLevel(root, 1));printf("KLevelSize:%d\n", TreeKLevel(root, 2));printf("KLevelSize:%d\n", TreeKLevel(root, 3));printf("KLevelSize:%d\n", TreeKLevel(root, 4));return 0;
}
5.2算法图解(递归)
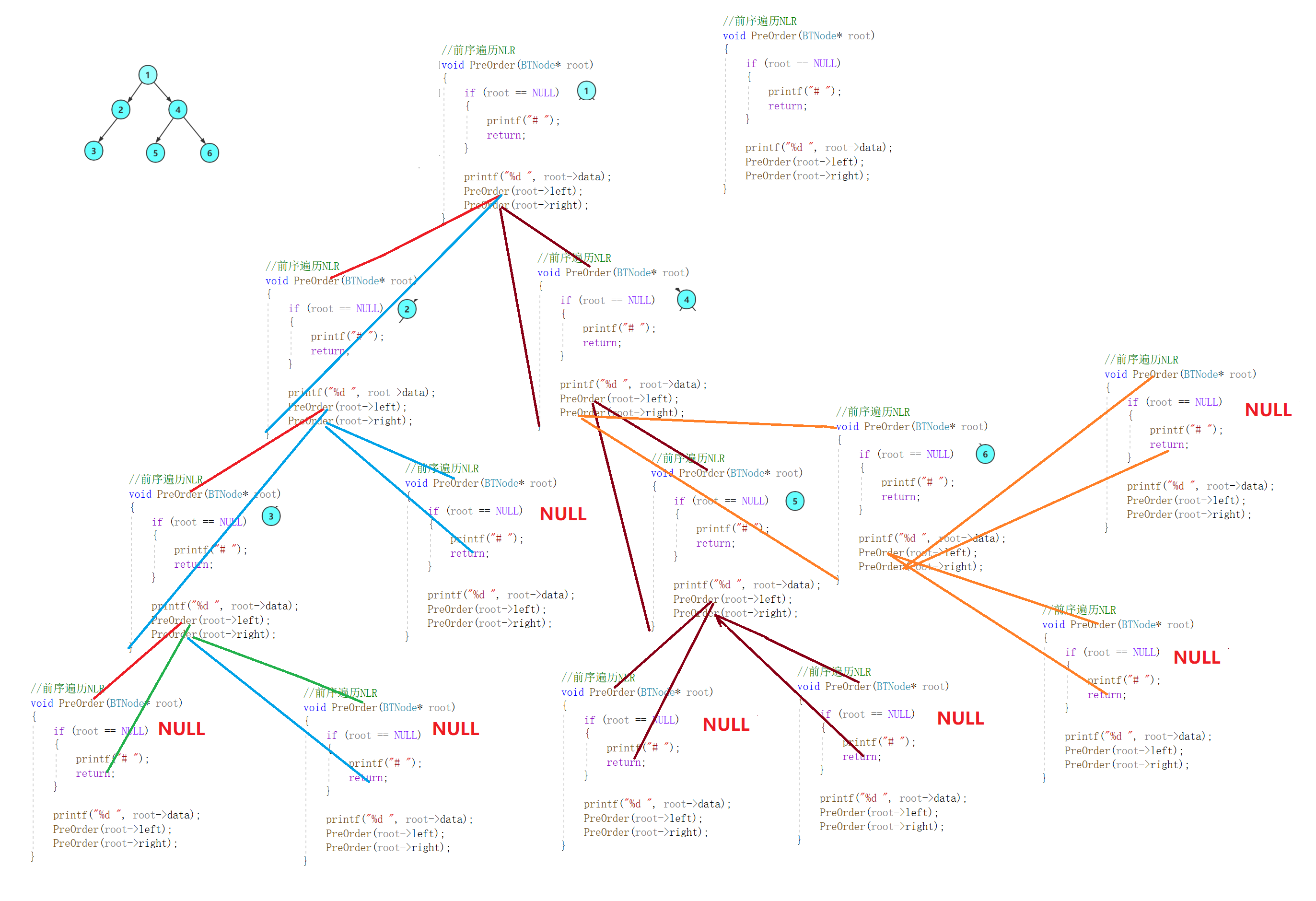
相关文章:

二叉树(C语言)
文章目录 1.树1.1概念1.2相关定义1.3 表示(左孩子右兄弟) 2.二叉树2.1概念2.2特殊的二叉树1. 满二叉树:2. 完全二叉树: 2.3二叉树的性质2.4练习 3.二叉树的存储结构1. 顺序存储2. 链式存储 4.完全二叉树的代码实现4.1堆的介绍1.堆…...
模块中的类forms.CharField)
介绍下Django中的表单(forms)模块中的类forms.CharField
在Django中,forms.CharField() 是用于定义表单字段的类,它属于 Django 的表单(forms)模块。CharField 是用于处理字符型数据的表单字段类。它允许用户在表单中输入文本数据,并对该数据进行验证和处理。 forms.CharFie…...

元宇宙与数字孪生的异同?
随着数字孪生和元宇宙两个概念的爆火,人们对这两个“异物”也越来越好奇,这都是什么意思?听起来都差不多,是一样的嘛?本文就用最简单的话语带大家了解一下二者之间的异同。 首先来说数字孪生和元宇宙的概念 数字孪生是…...
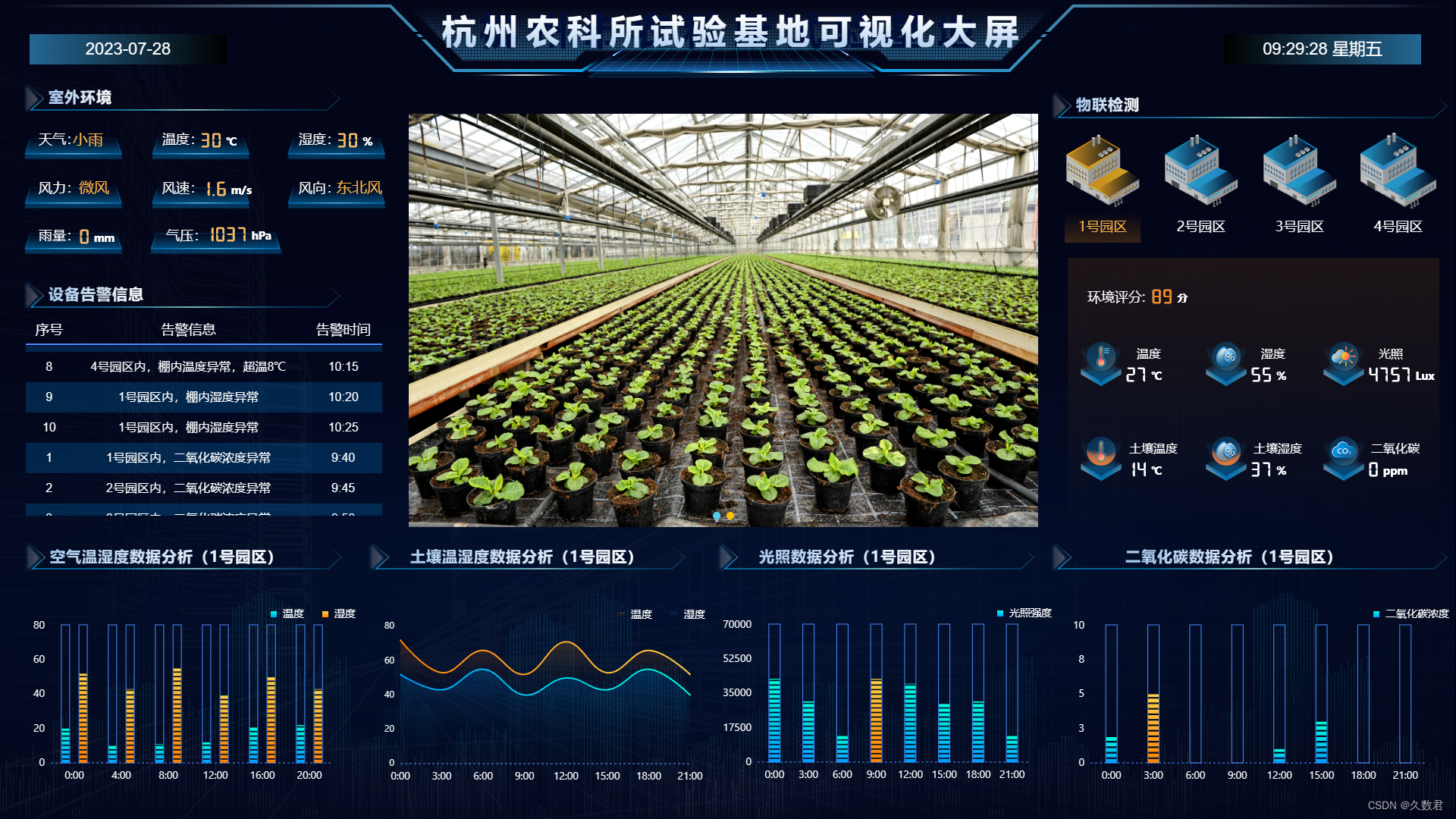
智慧农业:科技赋能农村发展
智慧农业发展前景灿烂多彩,正为农业带来新的转型升级。随着科技的不断发展,数字化、自动化和智能化技术逐渐渗透进农业领域,为农民提供了更多高效便捷的农业管理方式。智慧农业通过物联网、大数据、人工智能等先进技术,实现对农田…...
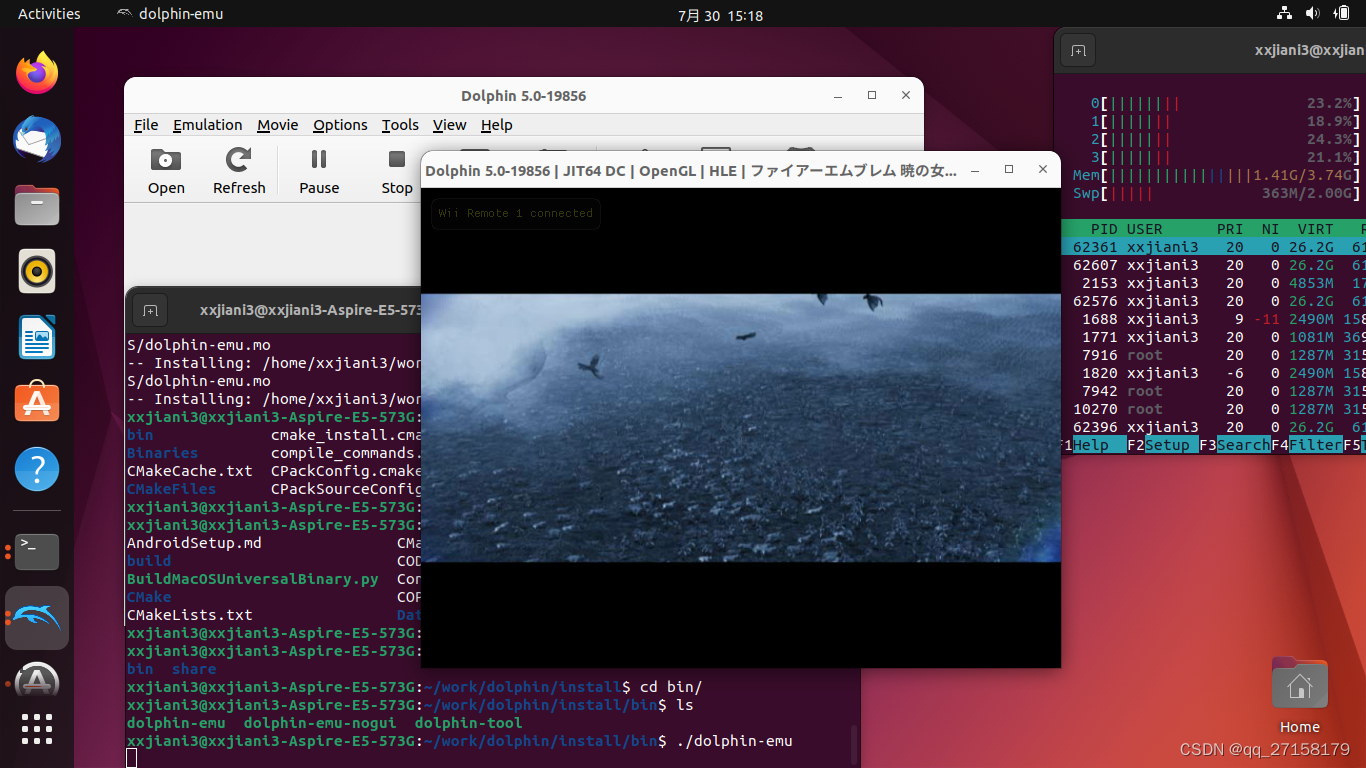
x86架构ubuntu22下运行WILL模拟器dophin
0. 环境 i5实体机ubuntu22 1. 安装依赖 $ sudo apt install build-essential git cmake ffmpeg libavcodec-dev libavformat-dev libavutil-dev libswscale-dev libevdev-dev libusb-1.0-0-dev libxrandr-dev libxi-dev libpangocairo-1.0-0 qt6-base-private-dev libblueto…...

Jvm的一些技巧
反编译字节码文件 找到对应的class文件所在的目录,使用javap -v -p 命令 查询运行中某个Java进程的Jvm参数 【案例】查询 MethodAreaDemo 这个类运行过程中,初始的元空间大小 MetaspaceSize jps 查询 Java 进程的进程ID 使用jinfo查看具体的参数&…...
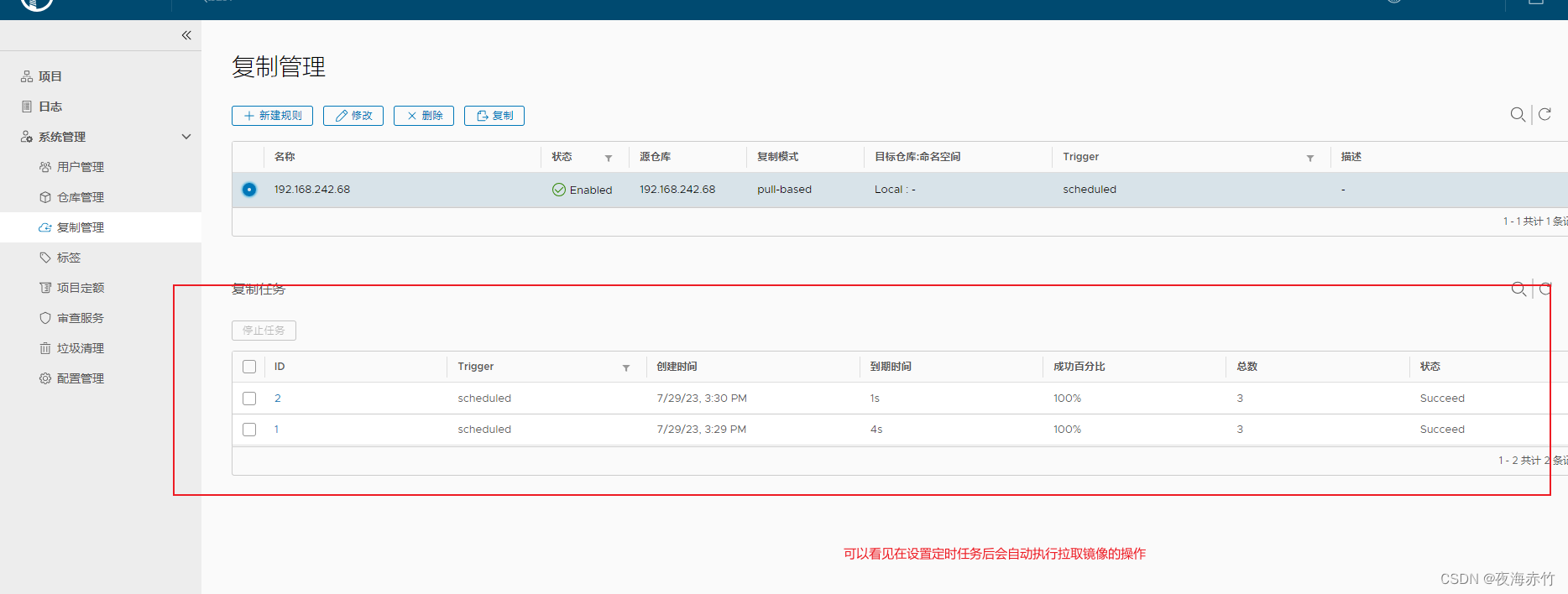
8.docker仓库
文章目录 Docker仓库本地私有仓库Docker HarborDocker harbor部署访问页面创建用户下载私有仓库镜像harbor同步 Docker仓库 本地私有仓库 ##先下载 registry 镜像docker pull registry##修改配置文件,在 daemon.json 文件中添加私有镜像仓库地址vim /etc/dock…...
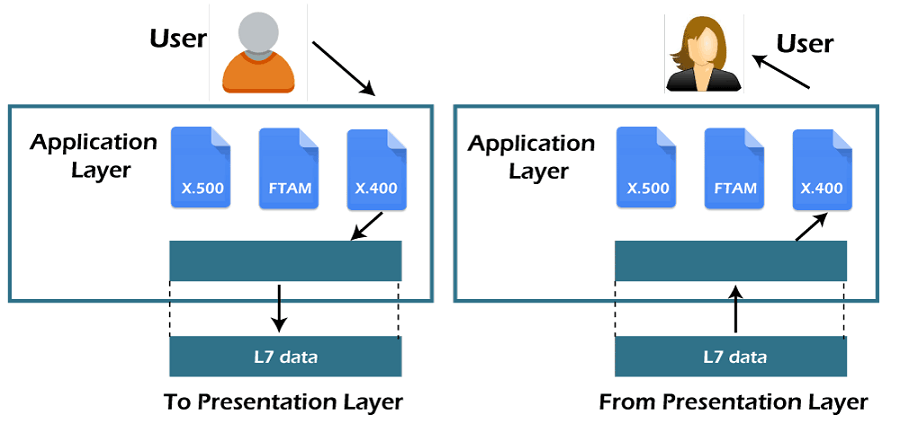
价值 1k 嵌入式面试题-计算机网络 OSI
开门见山 请讲下 OSI 各层协议的主要功能? 常见问题 回答不系统回答不确切无法和实际网络协议做关联对应 答题思路 OSI 代表了开放互联系统中信息从一台计算机的一个软件应用流到另一个计算机的另一个软件应用的参考模型 OSI 包含 7 层,每一层负责特…...

spring boot去除get post空格
1.用ControllerAdvice处理 package com.wangzs.handler;import com.fasterxml.jackson.core.JsonParser; import com.fasterxml.jackson.databind.DeserializationContext; import com.fasterxml.jackson.databind.deser.std.StdScalarDeserializer; import org.springframewo…...
)
设计模式四:单例模式(Singleton)
单例模式,是一种常用的软件设计模式。在它的核心结构中只包含一个被称为单例的特殊类。 通过单例模式可以保证系统中,应用该模式的类一个类只有一个实例。即一个类只有一个对象实例。 单例模式是设计模式中最简单的形式之一。这一模式的目的是使得类的一…...

《水经注地图服务》发布的影像数据如何在OsgEarth中调用
OsgEarth 是一个用于OpenSceneGraph (OSG)的可扩展地形渲染工具包,它是一个开源、高性能、3D 图形工具包。 只需创建一个简单的 XML 文件,将其指向您的图像、高程和矢量数据,将其加载到您最喜欢的 OSG 应用程序中,然后开始&#…...

css滤镜:drop-shadow
一、用法 drop-shadow( offset-x offset-y blur-radius spread-radius color ) offset-x:此参数设置图像的水平偏移。正值将创建右侧的偏移量,负值将创建左侧的偏移量。offset-y:此参数设置图像的垂直偏移。正值创建到底部的偏移量ÿ…...
java ThreadLocal
private ThreadLocal threadLocal new ThreadLocal(); threadLocal.set(0); (int) threadLocal.get(); 上面三行代码分别是定义、赋值和取值。 介绍: 我们只需要实例化对象一次,并且也不需要知道它是被哪个线程实例化。虽然所有的线程都能访问到这个T…...
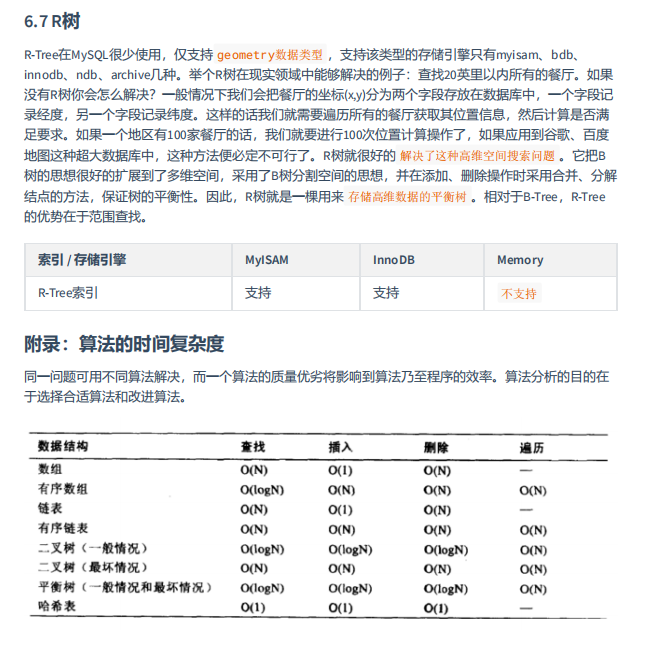
MySQL高级篇第6章(索引的数据结构)
文章目录 1、为什么使用索引2、索引及其优缺点3、InnoDB中索引的推演4、MyISAM中的索引方案5、索引的代价6、MySQL数据结构选择的合理性 1、为什么使用索引 假如给数据使用 二叉树 这样的数据结构进行存储,如下图所示 2、索引及其优缺点 3、InnoDB中索引的推演 4、M…...

Unity 性能优化三:动画模块、物理模块
目录 动画模块 Mecanim 模块 1.1 Animator active的数量 1.1.1 Culling Mode 1.1.2 Optimize Gameobject 1.1.3 Apply Root Motion 1.1.4 Compute Skinning 1.1.5 Animator Initialize 1.2 Legacy动画 物理模块 2.1 物理更新次数 2.1 减少不必要的Collision 2.5 A…...

延迟函数
Destory函数: public static void Destroy(Object obj, [DefaultValue("0.0F")] float t); Invoke函数: public void Invoke(string methodName, float time); 挂个空物体测试一下: public class DelayTest : MonoBehaviour {…...

IBM报告:2023数据泄露平均成本将达到445万美元
7月24日,IBM发布年度《数据泄露成本报告》显示,2023年全球数据泄露的平均成本达到445万美元,创该报告有史以来最高纪录,较过去3年均值增长了15%。同一时期,检测安全漏洞和漏洞恶化带来的安全成本上升了42&a…...
20.3 HTML 表格
1. table表格 table标签是HTML中用来创建表格的元素. table标签通常包含以下子标签: - th标签: 表示表格的表头单元格(table header), 用于描述列的标题. - tr标签: 表示表格的行(table row). - td标签: 表示表格的单元格(table data), 通常位于tr标签内, 用于放置单元格中的…...

flutter项目运行时一直卡在Running Gradle task ‘assembleDebug‘解决办法
1.修改项目中的android/build.gradle,将google(),mavenCentral()替换为下面的代码 maven { url https://maven.aliyun.com/repository/central/ }maven { url https://maven.aliyun.com/repository/public/ }maven { url https://maven.aliyun.com/repos…...

“深入理解Spring Boot:从入门到精通“
标题:深入理解Spring Boot:从入门到精通 摘要: Spring Boot是一款用于简化Spring应用开发的框架,它提供了一系列的开箱即用的功能和自动化配置,使得开发者能够快速构建、部署和运行Spring应用。本文将从入门到精通&am…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
