数据结构之常见排序算法
文章目录
- 1.排序概念
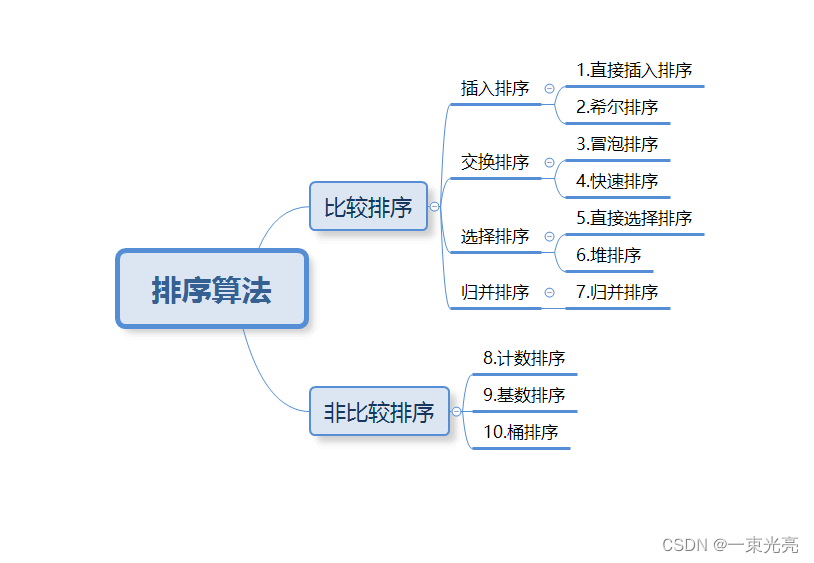
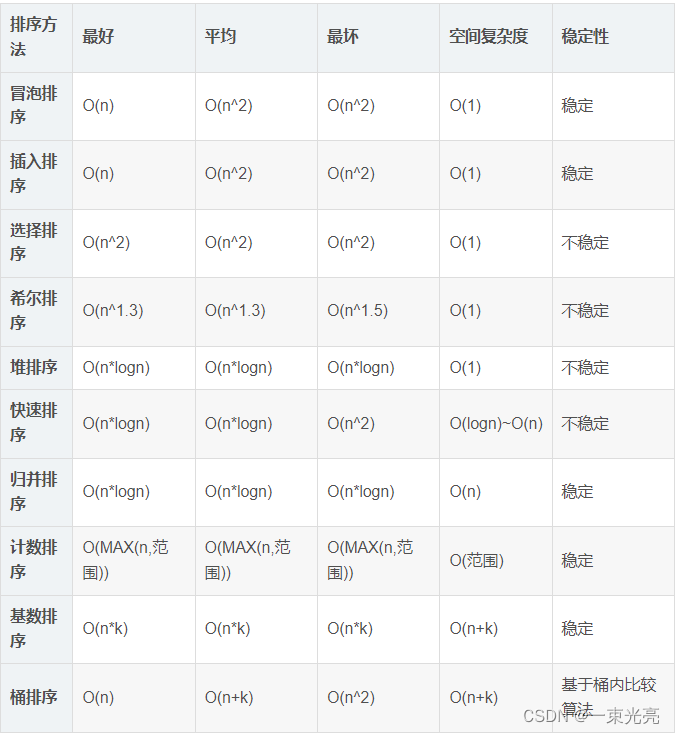
- 2.10种排序比较
- 3.排序算法
- 3.1直接插入排序(元素越有序,越高效)
- 3.2希尔排序序( 缩小增量排序 )
- 3.3直接选择排序
- 3.5堆排序
- 3.6冒泡排序
- 3.8快速排序 递归实现(无序使用最好)
- 3.8.1挖坑法 (建议用这个 找基准)
- 3.8.2Hoare法
- 3.8.3三数取中法 优化排序算法
- 3.9 快速排序 非递归实现
- 4.0归并排序
- 4.1计数排序
- 4.2基数排序
- 4.3桶排序
1.排序概念
排序:就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
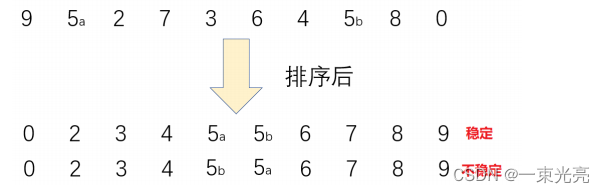
稳定性:假设一组序列中,有两个相同的元素,在排序之后,两个相同元素的前后顺序颠倒了,说明这个排序算法是不稳定的,反之。
2.10种排序比较
3.排序算法
3.1直接插入排序(元素越有序,越高效)
思路:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到
一个新的有序序列 。

/** 时间复杂度:最坏:o(N^2)* 最好:O(N) 数据都有序,j不会往前走,直接break* 当数据趋于有序的时候,排序速度非常快* 一般场景就是数据基本有序,建议使用直接插入排序* 空间复杂度:O(1)* 稳定性:稳定* 如果一个排序是稳定的,那么就可以实现为不稳定的,* 但是如果一个排序本身就是不稳定的,那么不能变成稳定的** */
//插入排序public static void insertSort(int[] array) {for (int i = 1; i < array.length; i++) {int temp = array[i];int j = i - 1;for (; j >= 0; j--) {if (array[j] > temp) {array[j + 1] = array[j];} else {break;}}array[j + 1] = temp;}}3.2希尔排序序( 缩小增量排序 )
基本思想:希尔排序是选的一个增量值分组,然后对每组使用直接插入排序算法排序,随着增量值减小,每组包含的值也越来越多,当增量值减为1时,整个序列在一组内排序
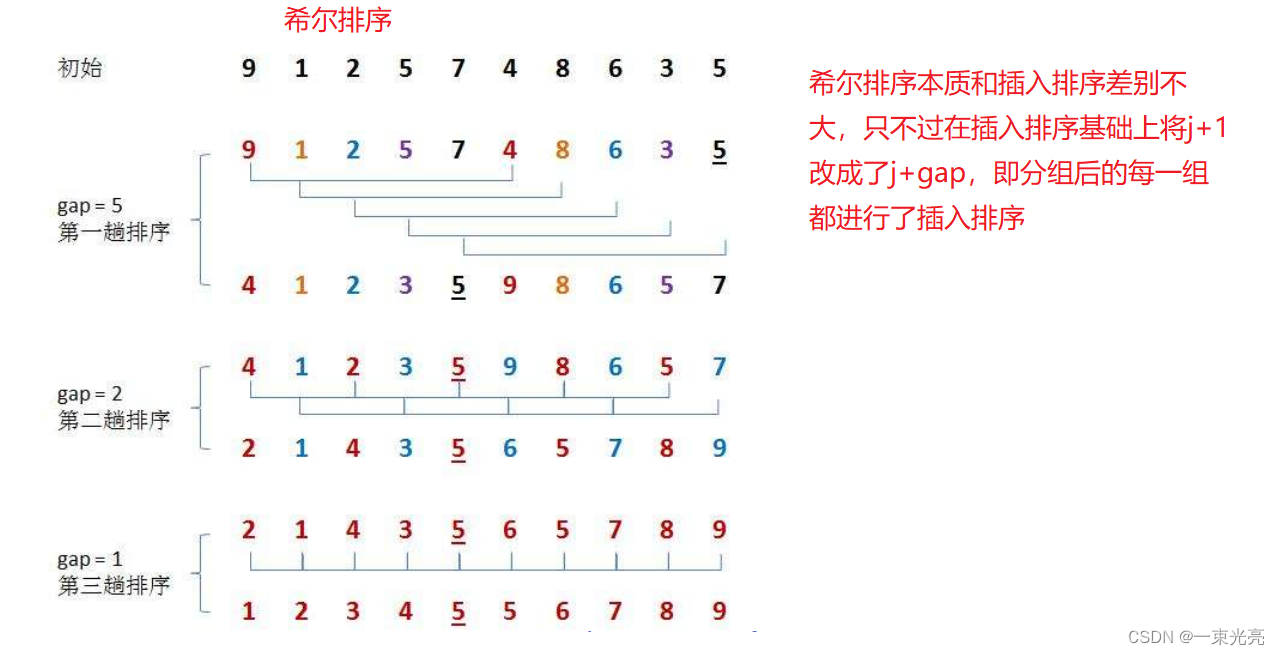
上代码:
//希尔排序 每组进行插入排序/*时间复杂度:O(N^1.3) - O(N ^ 1.5)*空间复杂度:o(1)* 稳定性:不稳定的排序**/public static void shellSort(int[] array) {int gap = array.length;while (gap > 1) {gap /= 2;shell(array, gap);}}//插入排序 ------->gappublic static void shell(int[] array, int gap) {for (int i = gap; i < array.length; i++) {int temp = array[i];int j = i - gap;for (; j >= 0; j -= gap) {if (array[j] > temp) {array[j + gap] = array[j];} else {break;}}array[j + gap] = temp;}}3.3直接选择排序
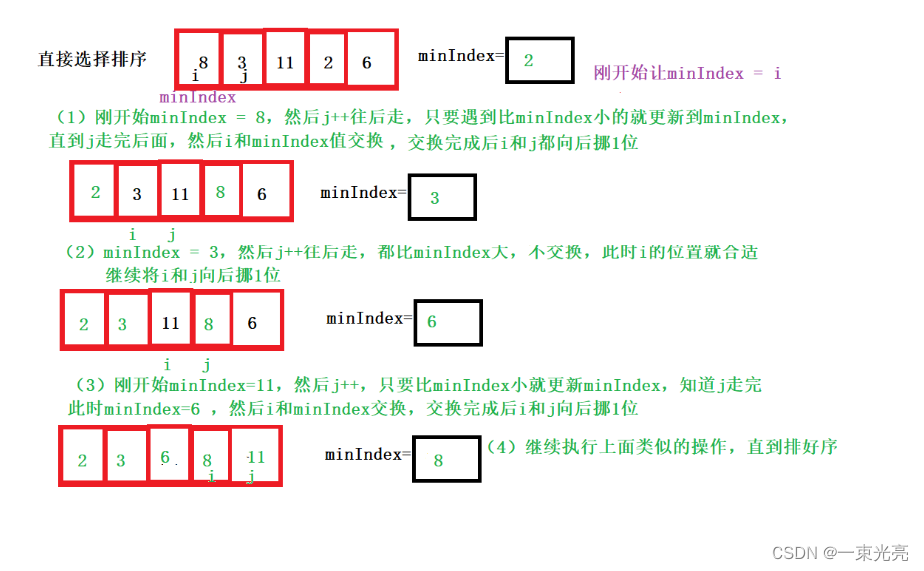
基本思想:在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
(1)第一种
/*选择排序*时间复杂度:O(N^2)* 空间复杂度:o(1)* 稳定性:不稳定** */public static void selectSort(int[] arrays) {for (int i = 0; i < arrays.length; i++) {int minIndex = i;for (int j = i + 1; j < arrays.length; j++) {if (arrays[j] < arrays[minIndex]) {minIndex = j;}}swap(arrays, i, minIndex);}}private static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}(2)前面是用了一个minIndex去找最小值然后交换,最后排序
那么如果用两个一个minIndex去找最小值,一个maxIndex去找最大值,然后用left指向前,right指向后,比如说是升序那就minIndex和left交换,maxIndex和right交换,这样效率应该是比第一种方法要快
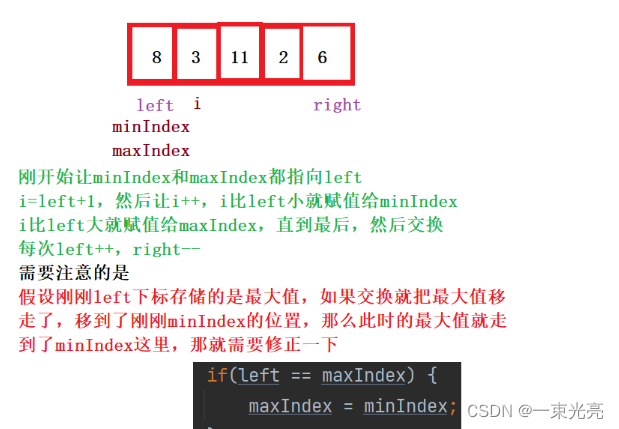
3.5堆排序
基本思想:堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
/*堆排序*时间复杂度:O(Nlogn)* 空间复杂度:O(1)* 稳定性:不稳定* */public static void heapSort(int[] array) {createBigHeap(array);int end = array.length - 1;while (end > 0) {swap(array, 0, end);shiftDown(array, 0, end);end--;}}private static void createBigHeap(int[] array) {for (int parent = (array.length - 1 - 1) / 2; parent >= 0; parent--) {shiftDown(array, parent, array.length);}}private static void shiftDown(int[] array, int parent, int len) {int child = parent * 2 + 1;//至少有左孩子while (child < len) {if (child + 1 < len && array[child] < array[child + 1]) {//有右孩子,且右孩子最大child++;}if (array[child] > array[parent]) {swap(array, child, parent);parent = child;child = 2 * parent + 1;} else {//child比parent小,不需要调整break;}}}3.6冒泡排序
基本思想:冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。重复的进行上面的步骤,直到没有再需要交换的
/** 冒泡排序* 时间复杂度:不考虑优化 O(N^2),优化后,o(N)*空间复杂度o(1)* 稳定性:稳定* */public static void bubbleSort(int[] array) {for (int i = 0; i < array.length; i++) {//考虑优化如果某一轮中没有发生交换,则证明已经有序,不必进行后面轮数boolean flg = false;for (int j = 0; j < array.length - 1 - i; j++) {if (array[j] > array[j + 1]) {swap(array, j, j + 1);flg = true;}}if (flg == false) {return;}}}private static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}3.8快速排序 递归实现(无序使用最好)
基本思想:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,
左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,
然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
在写递归的过程中可联想 二叉树的前序遍历 找基准值 进行区间划分
//快速排序/** 时间复杂度:N*logN* 最好情况:N*logN* 最坏情况:N^2 有序 倒序 (只有左树或者只有右树)* 空间复杂度:* 最好情况:logN* 最坏情况:N* 稳定性:不稳定** *///1.递归实现快速排序public static void quickSort(int[] array) {quick(array, 0, array.length - 1);}private static void quick(int[] array, int start, int end) {//递归结束条件//为什么取大于号 :1,2,3,4 越界if (start >= end) {return;}//基准int pivot = partition(array, start, end);//划分quick(array, start, pivot - 1);quick(array, pivot + 1, end);}//插入排序public static void insertSort2(int[] array, int start, int end) {for (int i = start + 1; i <= end; i++) {int temp = array[i];int j = i - 1;for (; j >= 0; j--) {if (array[j] > temp) {array[j + 1] = array[j];} else {break;}}array[j + 1] = temp;}}3.8.1挖坑法 (建议用这个 找基准)
必须先走右边,再走左边,这样就不会出现将大的放在前面的情况

//基准 挖坑法private static int partition(int[] array, int left, int right) {int tmp = array[left];while (left < right) {//left<right 不然会越界//“ = ”必须取,不然会发生死循环:6 23 1 3 6while (left < right && array[right] >= tmp) {right--;}array[left] = array[right];while (left < right && array[left] <= tmp) {left++;}array[right] = array[left];}array[left] = tmp;return left;}
3.8.2Hoare法
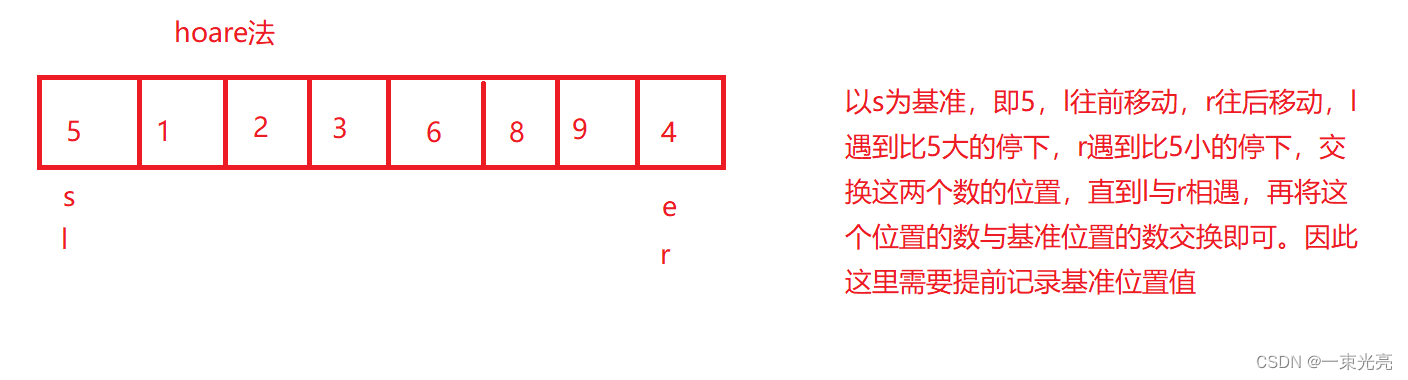
//Hoare法private static int partition2(int[] array, int left, int right) {int tmp = array[left];int i = left;while (left < right) {//为什么要先从右边走,因为左边先停下来就会比tmp大,与i位置交换就会把比tmp大的换到前面while (left < right && array[right] >= tmp) {right--;}while (left < right && array[left] <= tmp) {left++;}swap(array, left, right);}swap(array, left, i);return left;}3.8.3三数取中法 优化排序算法

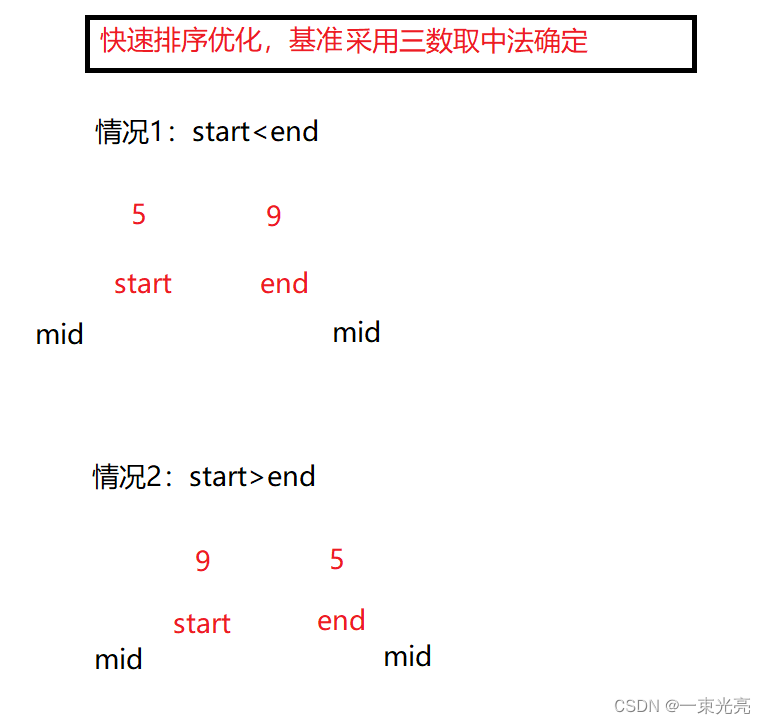
//1.递归实现快速排序public static void quickSort(int[] array) {quick(array, 0, array.length - 1);}private static void quick(int[] array, int start, int end) {//递归结束条件//为什么取大于号 :1,2,3,4 越界if (start >= end) {return;}//优化2:解决减少递归的次数if (end - start + 1 <= 14) {//假设有十万条数据,还剩十几条,那么数据基本有序,用插入排序更高效insertSort2(array, start, end);return;}// 三数取中法优化1:不用每一次都用start,而是从start ,mid ,end中取一个中间数来作为基准然后将它与start位置的数交换位置即可,// 后续不用改变int i = minThree(array, start, end);swap(array, i, start);//基准int pivot = partition2(array, start, end);//划分quick(array, start, pivot - 1);quick(array, pivot + 1, end);}//三数取中法private static int minThree(int[] array, int start, int end) {int mid = (start + end) / 2;if (start < end) {if (mid < start) {return start;} else if (mid > end) {return end;} else {return mid;}} else {if (mid < end) {return end;} else if (mid > start) {return start;} else {return mid;}}}3.9 快速排序 非递归实现
第一个分析:

第二个分析:
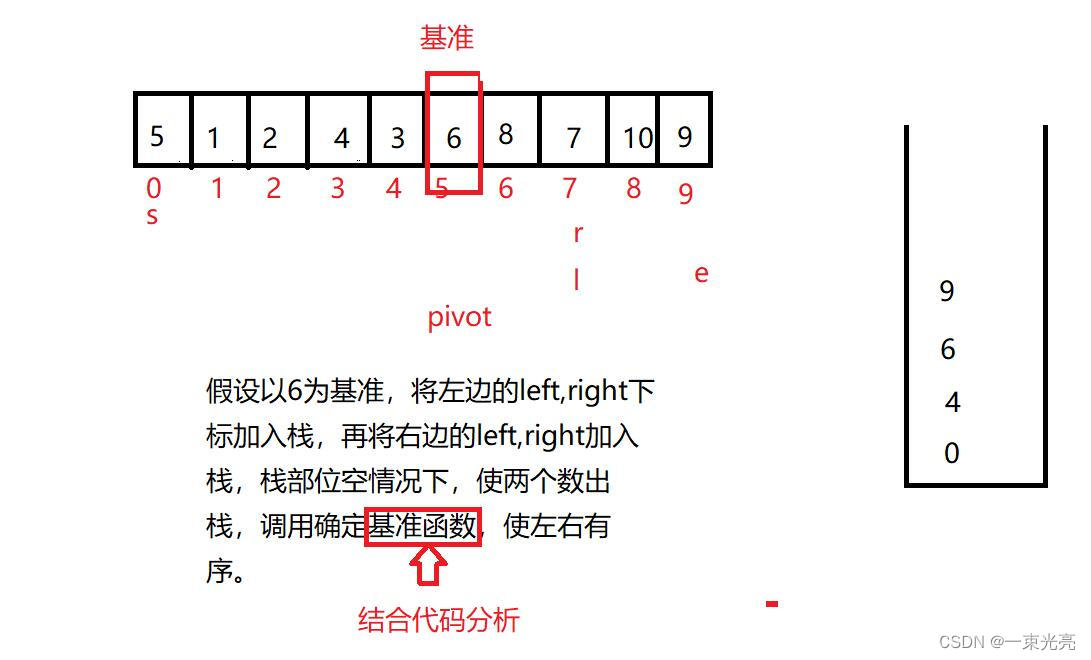
上代码:
//2.非递归实现快速排序/** 时间复杂度:O(Nlog n)* 空间复杂度:O(log n)* 稳定性:不稳定* */public static void quickSort2(int[] array) {Deque<Integer> stack = new LinkedList<>();int left = 0;int right = array.length - 1;int pivot = partition(array, left, right);//保证左边与右边都大于两个元素,才可以排序,只有一个元素就不用排序了if (pivot > left + 1) {stack.push(left);stack.push(pivot - 1);}if (pivot < right - 1) {stack.push(pivot + 1);stack.push(right);}while (!stack.isEmpty()) {right = stack.pop();left = stack.pop();pivot = partition(array, left, right);//保证左边与右边都大于两个元素,才可以排序,只有一个元素就不用排序了if (pivot > left + 1) {stack.push(left);stack.push(pivot - 1);}if (pivot < right - 1) {stack.push(pivot + 1);stack.push(right);}}}4.0归并排序
基本思想:归并排序是建立在归并操作上的一种有效的排序算法,将已有序的子序列合并,得到完全有序的序列;也就是先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
递归实现:
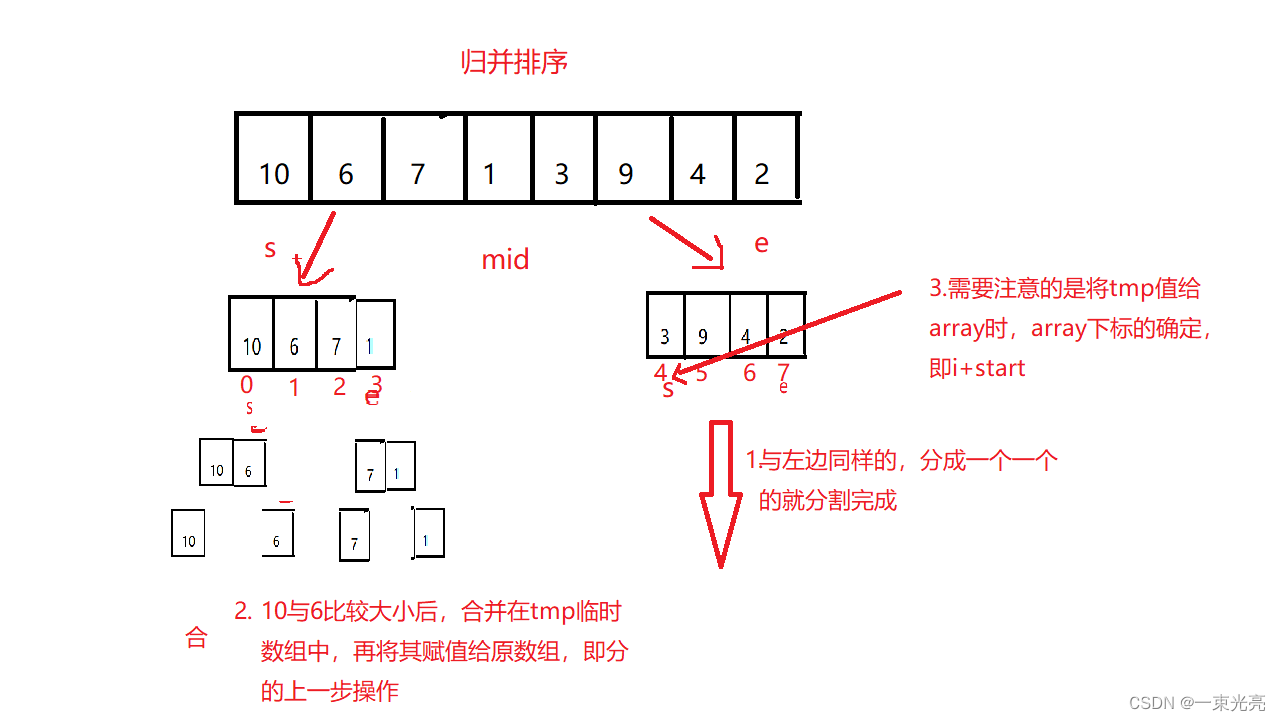
//归并排序public static void mergeSort(int[] array) {mergeSortFunc(array, 0, array.length - 1);}private static void mergeSortFunc(int[] array, int start, int end) {//和快速排序原因一样if (start >= end) {return;}int mid = (end + start) / 2;//分mergeSortFunc(array, start, mid);mergeSortFunc(array, mid + 1, end);//并merge(array, start, end, mid);}private static void merge(int[] array, int start, int end, int mid) {int s1 = start;int s2 = mid + 1;//tmp数组下标int k = 0;//合并成一个临时数组int[] tmp = new int[end - start + 1];while (s1 <= mid && s2 <= end) {if (array[s1] <= array[s2]) {tmp[k++] = array[s1++];} else {tmp[k++] = array[s2++];}}//s2数组为空时,s1还有数据while (s1 <= mid) {tmp[k++] = array[s1++];}//同样的while (s2 <= end) {tmp[k++] = array[s2++];}//将tmp临时数组数据给原数组for (int i = 0; i < tmp.length; i++) {//这里start+i意思是,不一定start都是0下标开始的array[i + start] = tmp[i];}}
非递归实现归并排序:
//非递归实现归并排序public static void mergeSort2(int[] array) {int gap = 1;while (gap < array.length) {//i += gap * 2,当前组拍序好后,i往后移动,排序下一组for (int i = 0; i < array.length; i += gap * 2) {int left = i;int mid = i + gap - 1;if (mid >= array.length) {避免越界异常mid = array.length - 1;}int right = mid + gap;//if (right >= array.length) {//避免越界异常right = array.length - 1;}merge(array, left, right, mid);}//间隙为1的每组排序好后,改为间隙为2的每组,重复上述步骤,接着排序下一组,直到gap//超过array.lengh,就排序好了gap *= 2;}}4.1计数排序
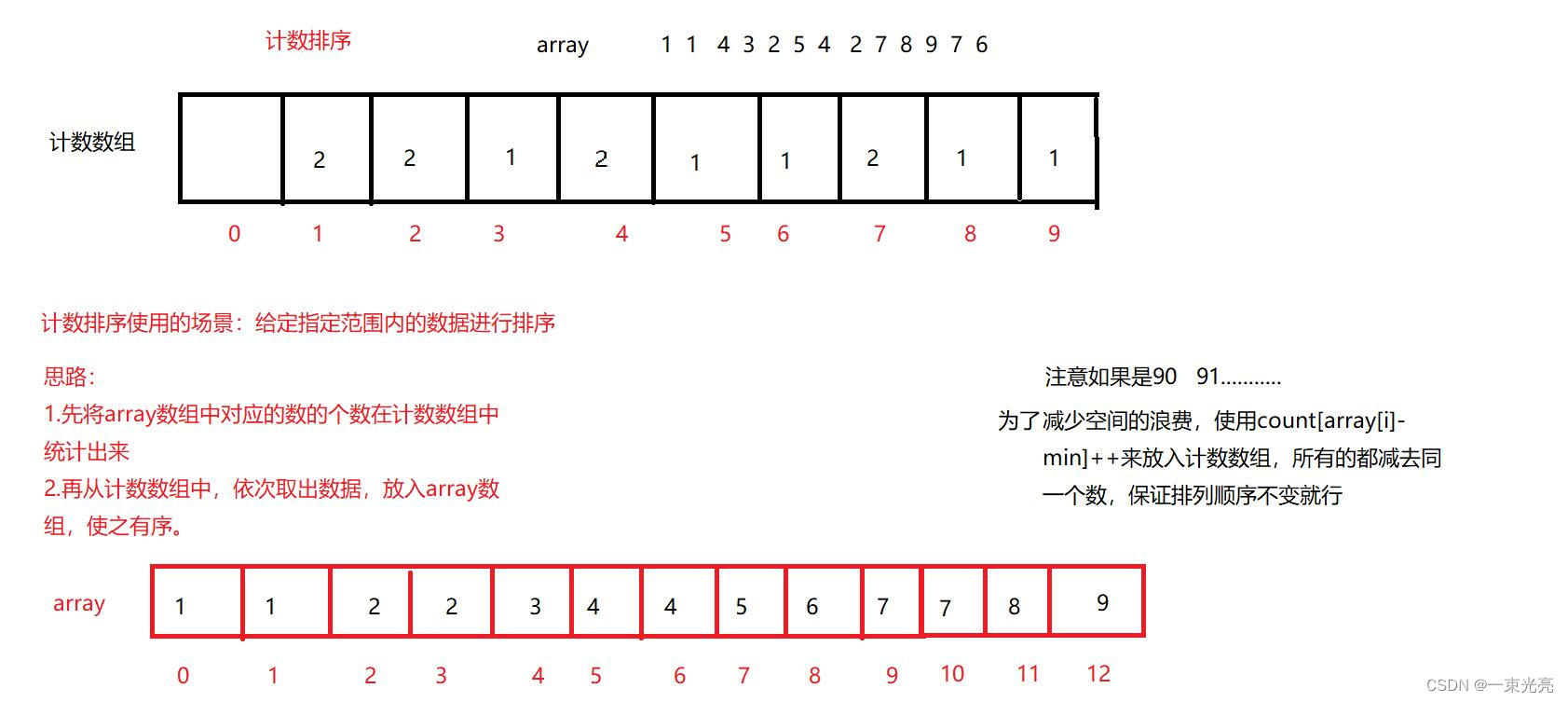
//计数排序/** 时间复杂度:O(N+范围)* 空间复杂度:** */public static void countSort(int[] array) {//1遍历数组,找到数组最大值和最小值int min = array[0];int max = array[0];for (int i = 1; i < array.length; i++) {if (array[i] < min) {min = array[i];}if (array[i] > max) {max = array[i];}}//2确定计数数组的长度int len = max - min + 1;int[] count = new int[len];//3遍历array数组,在计数数组中记录数字出现的个数for (int i = 0; i < array.length; i++) {count[array[i] - min]++;}//根据计数数组,将数字按照数组顺序重新返回array数组int index = 0;for (int i = 0; i < count.length; i++) {while (count[i] > 0) {//这里i+min:在array中加上min,反映真实数据array[index] = i + min;index++;count[i]--;}}}4.2基数排序
基本思想:基数排序是利用分配和收集两种基本操作。
基数排序是一种按记录关键字的各位值逐步进行排序的方法。
此种排序一般适用于记录的关键字为整数类型的情况。所有对于字符串和文字排序不适合。
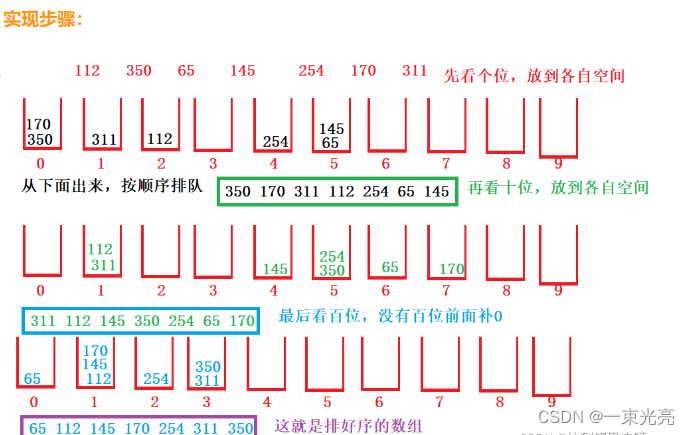
private static void radixSort(int[] arr) {//待排序列最大值int max = arr[0];int exp;//指数//计算最大值for (int anArr : arr) {if (anArr > max) {max = anArr;}}//从个位开始,对数组进行排序for (exp = 1; max / exp > 0; exp *= 10) {//存储待排元素的临时数组int[] temp = new int[arr.length];//分桶个数int[] buckets = new int[10];//将数据出现的次数存储在buckets中for (int value : arr) {//(value / exp) % 10 :value的最底位(个位)buckets[(value / exp) % 10]++;}//更改buckets[i],for (int i = 1; i < 10; i++) {buckets[i] += buckets[i - 1];}//将数据存储到临时数组temp中for (int i = arr.length - 1; i >= 0; i--) {temp[buckets[(arr[i] / exp) % 10] - 1] = arr[i];buckets[(arr[i] / exp) % 10]--;}//将有序元素temp赋给arrSystem.arraycopy(temp, 0, arr, 0, arr.length);}}4.3桶排序
基本思想:将要排序的数据分到几个有序的桶里,每个桶里的数据再单独进行排序。桶内排完序之后,再把每个桶里的数据按照顺序依次取出,组成的序列就是有序的了
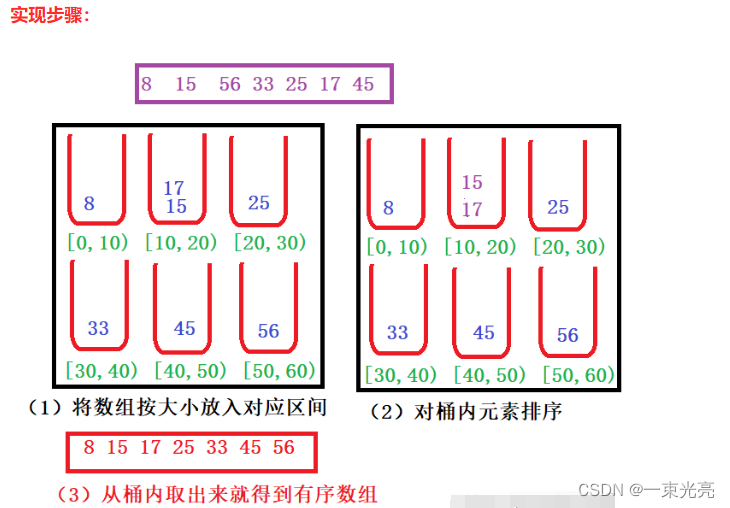
public static void bucketSort(int[] arr){// 计算最大值与最小值int max = Integer.MIN_VALUE;int min = Integer.MAX_VALUE;for(int i = 0; i < arr.length; i++){max = Math.max(max, arr[i]);min = Math.min(min, arr[i]);}// 计算桶的数量int bucketNum = (max - min) / arr.length + 1;ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);for(int i = 0; i < bucketNum; i++){bucketArr.add(new ArrayList<Integer>());}// 将每个元素放入桶for(int i = 0; i < arr.length; i++){int num = (arr[i] - min) / (arr.length);bucketArr.get(num).add(arr[i]);}// 对每个桶进行排序for(int i = 0; i < bucketArr.size(); i++){Collections.sort(bucketArr.get(i));}// 将桶中的元素赋值到原序列int index = 0;for(int i = 0; i < bucketArr.size(); i++){for(int j = 0; j < bucketArr.get(i).size(); j++){arr[index++] = bucketArr.get(i).get(j);}}
}
相关文章:

数据结构之常见排序算法
文章目录 1.排序概念2.10种排序比较3.排序算法3.1直接插入排序(元素越有序,越高效)3.2希尔排序序( 缩小增量排序 )3.3直接选择排序3.5堆排序3.6冒泡排序3.8快速排序 递归实现(无序使用最好)3.8.1挖坑法 (建…...
Java版企业电子招标采购系统源代码Spring Boot + 二次开发 + 前后端分离 构建企业电子招采平台之立项流程图
项目说明 随着公司的快速发展,企业人员和经营规模不断壮大,公司对内部招采管理的提升提出了更高的要求。在企业里建立一个公平、公开、公正的采购环境,最大限度控制采购成本至关重要。符合国家电子招投标法律法规及相关规范,以及审…...

2.2 模型与材质基础
一、渲染管线与模型基础 1. 渲染管线 可编程阶段(蓝色区域): 1顶点着色器 2几何着色器 3片元着色器 2. 模型的实现原理 UV:在建模软件中,进行UV展开,UV会放在一个横向为U纵向为V,范围࿰…...

什么是Docker
一 、什么是Docker 1.1 简介 Docker 使用 Google 公司推出的 Go 语言 (opens new window)进行开发实现,基于 Linux 内核的 cgroup (opens new window),namespace (opens new window),以及 OverlayFS (opens new window)类的 Union FS (open…...

1109. 航班预订统计
这里有 n 个航班,它们分别从 1 到 n 进行编号。 有一份航班预订表 bookings ,表中第 i 条预订记录 bookings[i] [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti (包含 firsti 和 lasti )的 每个航班 上预订了 seatsi 个座…...

[SQL挖掘机] - 窗口函数 - 合计: rollup
介绍: rollup 是一种用于在 sql 查询中生成聚合数据的特殊操作。它可以创建包含子总计和总计的结果集,并可用于生成层次化报表或汇总数据。 rollup 操作在 group by 子句中使用,可以在查询结果中生成多级汇总数据。它会根据指定的列进行分组࿰…...

2022年全国硕士研究生入学统一考试管理类专业学位联考写作试题——解析版
四、写作:第56~57小题,共65分。其中论证有效性分析30分,论说文35分。 56.论证有效性分析:分析下述论证中存在的缺陷和漏洞,选择若干要点,写一篇600字左右的文章,对该论证的有效性进…...

元类在测试框架中的运用
元类在测试框架中的运用 书接上回 我们知道了元类的基本用法,也写了一个小demo,接下来我们就尝试运用进我们测试框架。 #一款无需编码且易用于二次开发的接口测试框架。 #我写的我写的我写的我写的 pip install mwj-apitest #这里面就用到了元类&…...

VBA快速交叉分段标记字符颜色
实例需求:A列中有不确定行数的数据,现在需要将数据按照每4位一组间隔标记颜色,如下图所示。 示例代码如下。 Sub Demo()Dim rngCell As RangeDim rngData As RangeDim i, res, intLenSet rngData Range("A1").CurrentRegionrngDa…...

根据Pytorch源码实现的 ResNet18
一,类模块定义: import torch import torch.nn as nn import torch.nn.functional as F from torch import Tensorclass ResBlock(nn.Module):def __init__(self, inchannel, outchannel, stride1) -> None:super(ResBlock, self).__init__()# 这里定义了残差块…...
药品管理系统servlet+jsp+sql医院药店仓库进销存java源代码mysql
本项目为前几天收费帮学妹做的一个项目,Java EE JSP项目,在工作环境中基本使用不到,但是很多学校把这个当作编程入门的项目来做,故分享出本项目供初学者参考。 一、项目描述 药品管理系统servletjspsql 系统有1权限:…...

这9个UI设计工具一定码住!非常好用
对于设计师来说,好用的UI设计工具无疑会对设计工作起到事半功倍的作用,今天本文与大家分享9个好用的UI设计工具,一起来看看吧! 1、即时设计 即时设计是一个能在网页中直接使用,且支持团队协作的国产UI设计工具&#…...

gin通过反射来执行动态的方法
在gin中,可以通过反射来执行对应的方法。下面是一个示例: package mainimport ("fmt""github.com/gin-gonic/gin""reflect" )type UserController struct{}func (uc *UserController) GetUser(c *gin.Context) {userId :…...
java高并发系列 - 第23天:JUC中原子类,一篇就够了
java高并发系列 - 第23天:JUC中原子类 这是java高并发系列第23篇文章,环境:jdk1.8。 本文主要内容 JUC中的原子类介绍介绍基本类型原子类介绍数组类型原子类介绍引用类型原子类介绍对象属性修改相关原子类预备知识 JUC中的原子类都是都是依靠volatile、CAS、Unsafe类配合…...
《HeadFirst设计模式(第二版)》第一章源码
代码文件目录结构: FlyBehavior.java package Chapter1_StrategyPattern.ch1_3_behavior.behaviors.fly;public interface FlyBehavior {void fly(); } FlyNoWay.java package Chapter1_StrategyPattern.ch1_3_behavior.behaviors.fly;public class FlyNoWay imp…...
insert into select用法
文章目录 一、insert into select二、insert into select插入失败 本篇文章主要讲解insert into select 的用法,以及insert into select的坑或者注意事项。本篇文章中的sql基于mysql8.0进行讲解 一、insert into select 该语法常用于从另一张表查询数据插入到某表中…...

图像识别技术:计算机视觉的进化与应用展望
导言: 图像识别技术是计算机视觉领域的重要研究方向,它使计算机能够理解和解释图像内容,从而实现自动化和智能化的图像处理。随着深度学习等技术的快速发展,图像识别在诸多领域取得了重大突破,如自动驾驶、医疗影像分析…...

【免费送书】重新定义Python学习!
欢迎关注博主 Mindtechnist 或加入【智能科技社区】一起学习和分享Linux、C、C、Python、Matlab,机器人运动控制、多机器人协作,智能优化算法,滤波估计、多传感器信息融合,机器学习,人工智能等相关领域的知识和技术。关…...

Qt 4. 发布exe
把ex2.exe放在H盘Ex2文件夹下,执行 H:\Ex2>windeployqt ex2.exe H:\Ex2>windeployqt ex2.exe H:\Ex2\ex2.exe 64 bit, release executable Adding Qt5Svg for qsvgicon.dll Skipping plugin qtvirtualkeyboardplugin.dll due to disabled dependencies (Qt5…...

消息队列的使用场景以及优缺点
消息队列是一种在应用系统之间传递消息的通信模式。它允许发送者将消息发布到一个队列中,而接收者则从队列中获取消息进行处理。 消息队列的主要特点包括: 异步通信:消息的发送和接收是异步进行的,发送者无需等待接收者的即时响应…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...