机器学习深度学习——softmax回归的简洁实现
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er
🌌上期文章:机器学习&&深度学习——softmax回归从零开始实现
📚订阅专栏:机器学习&&深度学习
希望文章对你们有所帮助
继续使用Fashion-MNIST数据集,并保持批量大小为256:
import torch
from torch import nn
from d2l import torch as d2lbatch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
softmax回归的简洁实现
- 初始化模型参数
- 重新审视softmax的实现
- 数学推导
- 交叉熵函数
- 优化算法
- 训练
初始化模型参数
softmax的输出层是一个全连接层,因此,为了实现模型,我们只需要在Sequential中添加一个带有10个输出的全连接层。当然这里的Sequential并不是必要的,但是他是深度模型的基础。我们仍旧以均值为0,标准差为0.01来随机初始化权重。
# pytorch不会隐式地调整输入的形状
# 因此在线性层前就定义了展平层flatten,来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))def init_weights(m):if type(m) == nn.Linear:nn.init.normal_(m.weight, std=0.01)net.apply(init_weights) # 给net每一层跑一次init_weights函数
重新审视softmax的实现
数学推导
在之前的例子里,我们计算了模型的输出,然后将此输出送入交叉熵损失。看似合理,但是指数级计算可能会造成数值的稳定性问题。
回想一下之前的softmax函数:
y ^ j = e x p ( o j ) ∑ k e x p ( o k ) 其中 y ^ j 是预测的概率分布, o j 是未规范化的第 j 个元素 \hat{y}_j=\frac{exp(o_j)}{\sum_kexp(o_k)}\\ 其中\hat{y}_j是预测的概率分布,o_j是未规范化的第j个元素 y^j=∑kexp(ok)exp(oj)其中y^j是预测的概率分布,oj是未规范化的第j个元素
由于o中的一些数值会非常大,所以可能会让其指数值上溢,使得分子或分母变成inf,最后得到的预测值可能变成的0、inf或者nan。此时我们无法得到一个明确的交叉熵值。
提出解决这个问题的一个技巧:在继续softmax计算之前,先从所有的o中减去max(o),修改softmax函数的构造且不改变其返回值:
y ^ j = e x p ( o j − m a x ( o k ) ) e x p ( m a x ( o k ) ) ∑ k e x p ( o j − m a x ( o k ) ) e x p ( m a x ( o k ) ) \hat{y}_j=\frac{exp(o_j-max(o_k))exp(max(o_k))}{\sum_kexp(o_j-max(o_k))exp(max(o_k))} y^j=∑kexp(oj−max(ok))exp(max(ok))exp(oj−max(ok))exp(max(ok))
这样操作以后,可能会使得一些分子的exp(o-max(o))有接近0的值,即为下溢。这些值可能会四舍五入为0,这样就会使得预测值为0,那么此时要是取对数以后就会变为-inf。要是这样反向传播几步,我们可能会发现自己屏幕有一堆的nan。
尽管我们需要计算指数函数,但是我们最终会在计算交叉熵损失的时候会取他们的对数。尽管通过将softmax和交叉熵结合在一起,可以避免反向传播过程中可能会困扰我们的数值稳定性问题。如下面的式子:
l o g ( y ^ j ) = l o g ( e x p ( o j − m a x ( o k ) ) ∑ k e x p ( o k − m a x ( o k ) ) ) = l o g ( e x p ( o j − m a x ( o k ) ) ) − l o g ( ∑ k e x p ( o k − m a x ( o k ) ) ) = o j − m a x ( o k ) − l o g ( ∑ k e x p ( o k − m a x ( o k ) ) ) log(\hat{y}_j)=log(\frac{exp(o_j-max(o_k))}{\sum_kexp(o_k-max(o_k))})\\ =log(exp(o_j-max(o_k)))-log(\sum_kexp(o_k-max(o_k)))\\ =o_j-max(o_k)-log(\sum_kexp(o_k-max(o_k))) log(y^j)=log(∑kexp(ok−max(ok))exp(oj−max(ok)))=log(exp(oj−max(ok)))−log(k∑exp(ok−max(ok)))=oj−max(ok)−log(k∑exp(ok−max(ok)))
通过上式,我们避免了计算单独的exp(o-max(o)),而是直接使用o-max(o)。
因此,我们计算交叉熵函数的时候,传递的不是未规范化的预测o,而不是softmax。
但是我们也希望保留传统的softmax函数,以备我们要评估通过模型输出的概率。
交叉熵函数
在这里介绍一下交叉熵函数,以用于上面推导所需的需求:
torch.nn.CrossEntropyLoss(weight=None,ignore_index=-100,reduction='mean')
交叉熵函数是将LogSoftMax和NLLLoss集成到一个类中,通常用于多分类问题。其参数使用情况:
ignore_index:指定被忽略且对输入梯度没有贡献的目标值。
reduction:string类型的可选项,可在[none,mean,sum]中选。none表示不降维,返回和target一样的形状;mean表示对一个batch的损失求均值;sum表示对一个batch的损失求和。
weight:是一个一维的张量,包含n个元素,分别代表n类的权重,在训练样本不均衡时很有用,默认为None:
(1)当weight=None时,损失函数计算方式为
loss(x,class)=-log(exp(x[class])/Σexp(x[j]))=-x[class]+log(Σexp(x[j])
(2)当weight被指定时,损失函数计算方式为:
loss(x,class)=weight[class]×(-x[class]+log(Σexp(x[j]))
# 在交叉熵损失函数中传递未归一化的预测,并同时计算softmax及其导数
loss = nn.CrossEntropyLoss(reduction='none')
优化算法
# 优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.1)
训练
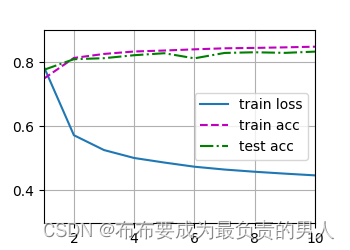
调用之前定义的训练函数来训练模型:
# 调用之前的训练函数来训练模型
num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
d2l.plt.show()
相关文章:

机器学习深度学习——softmax回归的简洁实现
👨🎓作者简介:一位即将上大四,正专攻机器学习的保研er 🌌上期文章:机器学习&&深度学习——softmax回归从零开始实现 📚订阅专栏:机器学习&&深度学习 希望文章对你…...
CPU利用率过高解决思路
文章目录 问题场景问题定位问题解决 本文参考: Linux服务器之CPU过高解决思路_linux cpu温度过高_Jeremy_Lee123的博客-CSDN博客 Java程序员必备:jstack命令解析 - 掘金 (juejin.cn) 重点问题!CPU利用率过高排查思路|原创 (qq.…...

Redis(三)—— Redis基本的事务操作、Redis实现乐观锁
一、Redis基本的事务操作 首先声明: redis的单条命令是保证原子性的(回想一下setnx k1 v1 k5 v5命令如果k1已经存在,那么k5也会设置失败)但是redis的事务不保证原子性!见下面“1.2 某条命令有错怎么办?”…...

SQLI_LABS攻击
目录 Less1 首先来爆字段 联合注入 判断注入点 爆数据库名 爆破表名 information_schema information_schmea.tables group_concat() 爆破列名 information_schema.columns 爆值 SQLMAP Less-2 -4 Less -5 布尔 数据库 表名 字段名 爆破值 SQLMAP Less-6 …...

如何查看 Chrome 网站有没有前端 JavaScript 报错?
您可以按照以下步骤在Chrome中查看网站是否存在前端JavaScript报错: 步骤1:打开Chrome浏览器并访问网站 首先,打开Chrome浏览器并访问您想要检查JavaScript报错的网站。 步骤2:打开开发者工具 在Chrome浏览器中,按…...
JS前端读取本地上传的File文件对象内容(包括Base64、text、JSON、Blob、ArrayBuffer等类型文件)
读取base64图片File file2Base64Image(file, cb) {const reader new FileReader();reader.readAsDataURL(file);reader.onload function (e) {cb && cb(e.target.result);//即为base64结果}; }, 读取text、JSON文件File readText(file, { onloadend } {}) {const re…...
【项目方案】OpenAI流式请求实现方案
文章目录 实现目的效果比对非stream模式stream模式实现方案方案思路总体描述前端方案对比event-source-polyfill代码示例前端实现遇到的问题与解决方法后端参考资料时序图关键代码示例后端实现时遇到的问题与解决方法实现目的 stream是OpenAI API中的一个参数,用于控制请求的…...
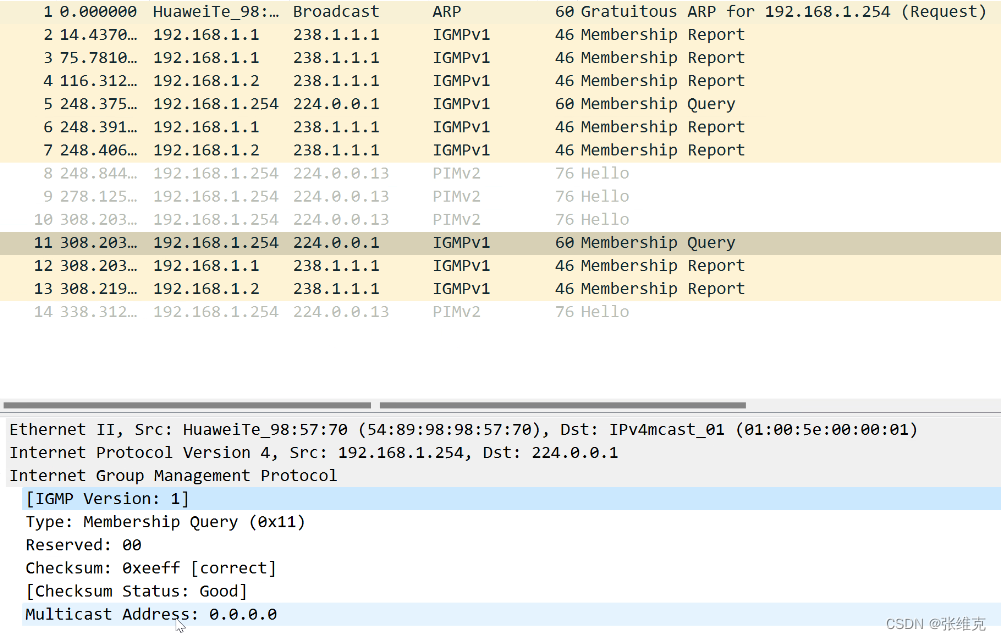
华为数通HCIP-IP组播基础
点到点业务:比如FTP,WEB业务,此类业务主要特点是不同的用户有不同的需求,比如用户A需要下载资料A,用户B需要下载资料B。此类业务一般由单播承载,服务器对于不同用户发送不同的点到点数据流。 ospf、isis…...

STM32 SPI学习
SPI 串行外设设备接口(Serial Peripheral Interface),是一种高速的,全双工,同步的通信总线。 SCK时钟信号由主机发出。 SPI接口主要应用在存储芯片。 SPI相关引脚:MOSI(输出数据线ÿ…...

分布式缓存与数据库的一致性记录
用户更新数据库,需要再去更新redis缓存,否则会造成缓存与数据库数据不一致 一致性的两种方法 1). 双写模式 更新完数据库之后,更新redis缓存数据 问题: 因为请求时间的问题,造成缓存数据不是最新的 数据。 原因:A先修…...

vue3的语法
main.js中写发生变化,并不兼容vue2的写法 //vue3 import { createApp } from vue import ./style.css import App from ./App.vuecreateApp(App).mount(#app)//vue2 import Vue from vue import ./style.css import App from ./App.vueconst vm new Vue({render:h…...

【git合并分支自定义提交消息】
开发分支 dev主分支 master 需求 dev分支开发完后合并到master分支自定义提交信息 通过 git merge dev --squash --no-commit此命令会拉取dev分支代码到当前分支,并不会自动提交,可以自己修改提交信息...
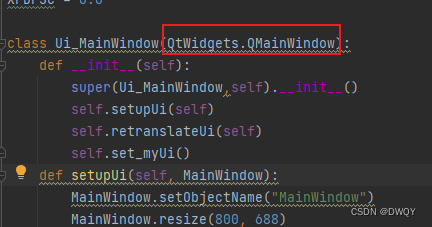
AttributeError: module ‘PyQt5.QtGui‘ has no attribute ‘QMainWindow‘
场景描述: 这个问题是使用PyUIC将ui文件变成py文件后遇到的 解决办法: 改动1:把object改成QtWidgets.QMainWindow 改动2:增加__init__函数,函数结构如下: def __init__(self):super(Ui_MainWindow,self).…...

基于Java+SpringBoot+Vue前后端分离电商项目
晚间lucky为友友们送福利啦~🎁 Tips:有需要毕业设计指导的童鞋一定要认真看哦,文末有彩蛋。 一.项目介绍 该电商项目是一个简单、入门级的电商项目,是基于JavaSpringBootVue前后端分离项目。前端采用两套独立的系统分别完成项目…...
实现思路)
Rpc服务消费者(Rpc服务调用者)实现思路
Rpc服务消费者(Rpc服务调用者)实现思路 前面几节说到Rpc消费者主要通过UserServiceRPc_Stub这个protobuf帮我们生成的类来实现,上代码回顾一下 class UserServiceRpc_Stub : public UserServiceRpc {public:UserServiceRpc_Stub(::PROTOBUF…...
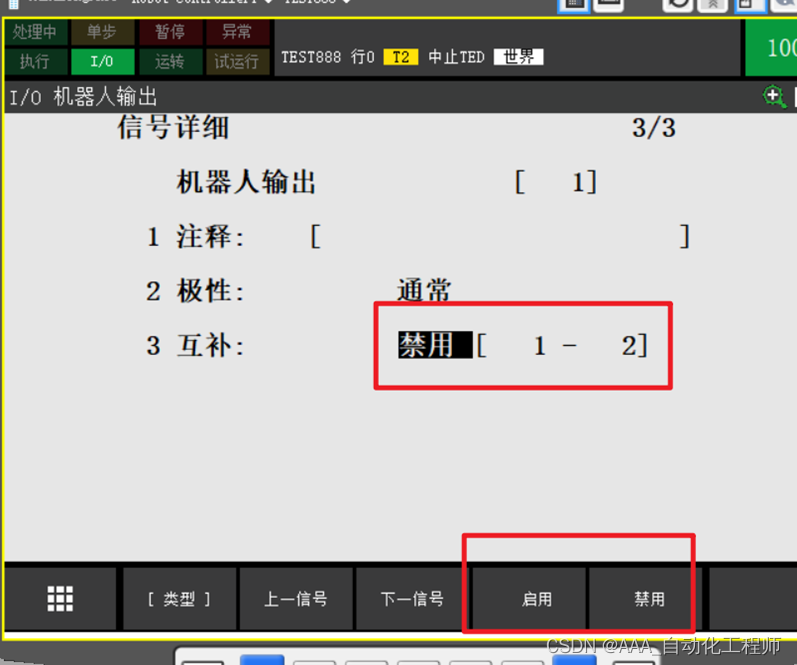
FANUC机器人实现2个RO输出信号互锁关联(互补)的具体方法
FANUC机器人实现2个RO输出信号互锁关联(互补)的具体方法 一般情况下,为了方便用户控制工装夹具上的电磁阀等控制工具,FANUC机器人出厂时给我们提供了8个RO输出信号,如下图所示,这8个RO信号可以各自单独使用。 那么,如果为了安全控制,需要将2个RO信号成对的进行安全互锁…...

权威认可|云畅科技再次入选中国信通院「高质量数字化转型产品及服务全景图」
7月27日,由中国信通院主办的2023数字生态发展大会暨中国信通院“铸基计划”年中会议在北京成功召开。 会上,中国信通院重磅发布了「高质量数字化转型产品及服务全景图(2023)」,云畅科技凭借其自研产品「万应低代码」在…...
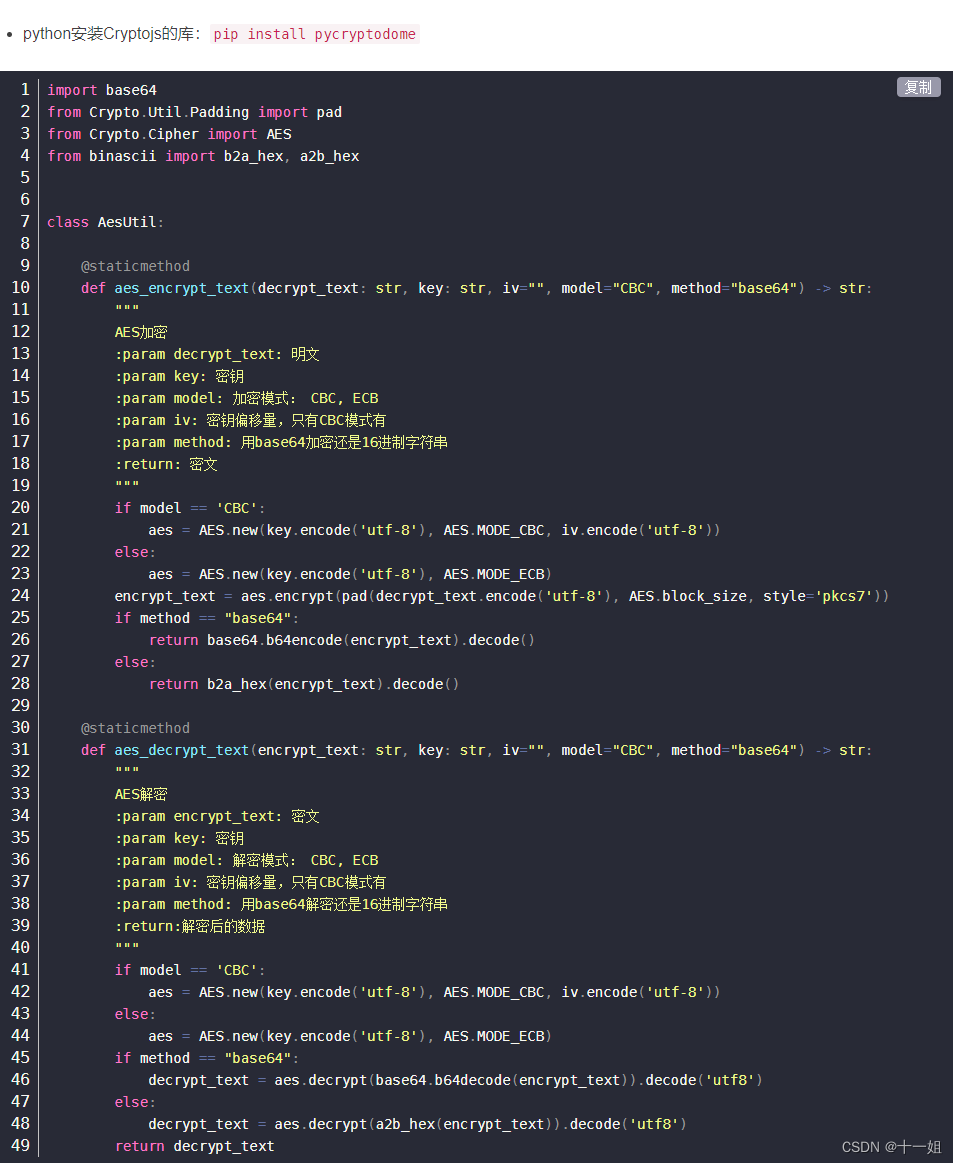
爬虫小白-如何调试列表页链接与详情链接不一样并三种方式js逆向解决AES-ECB
目录 一、网站分析二、定位监听三、熟悉AES-ECB四、调试分析五、node运行js六、Python执行js 一、网站分析 三年前的案例,我的原始文章网站 ,如图我们直接点击标题进入到详情页,链接会发生跳转,且与我们在详情看到的链接…...
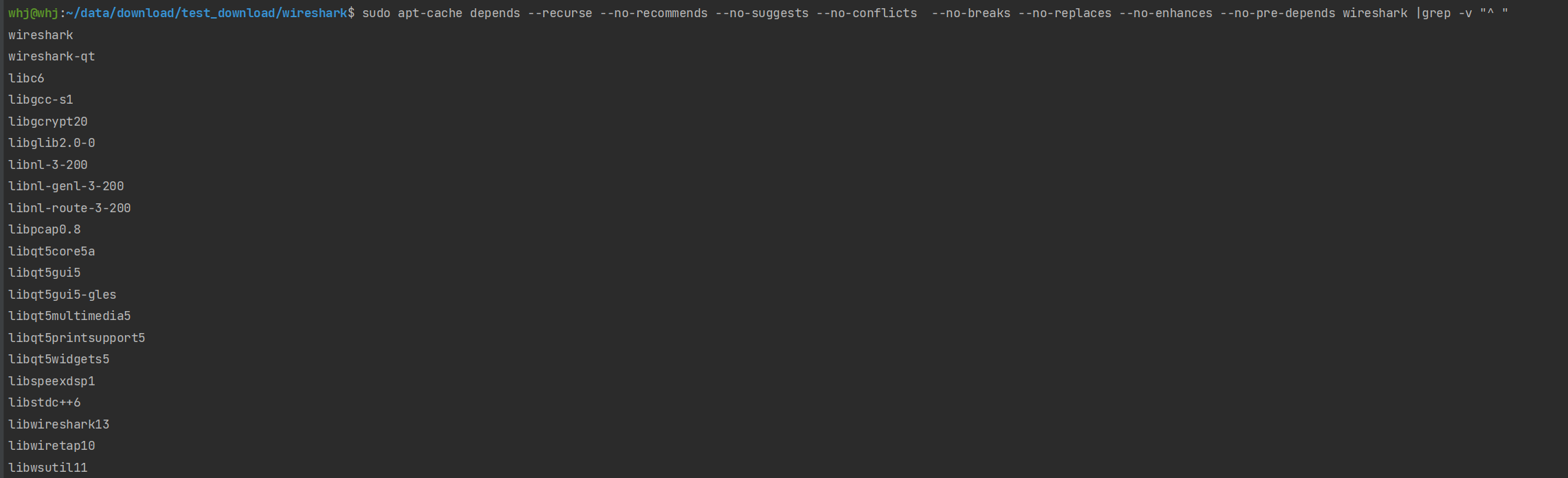
Ubuntu 离线部署的常见操作
Ubuntu 离线安装的常见操作 **说明:**很多情况下,生产环境都是离线环境,然而开发环境都是互联网的环境,因此部署的过程中需要构建离线安装包; 1. 下载但是不安装 # 例如使用 apt 下载 wireshark 安装包 sudo apt download wireshark # 下载…...
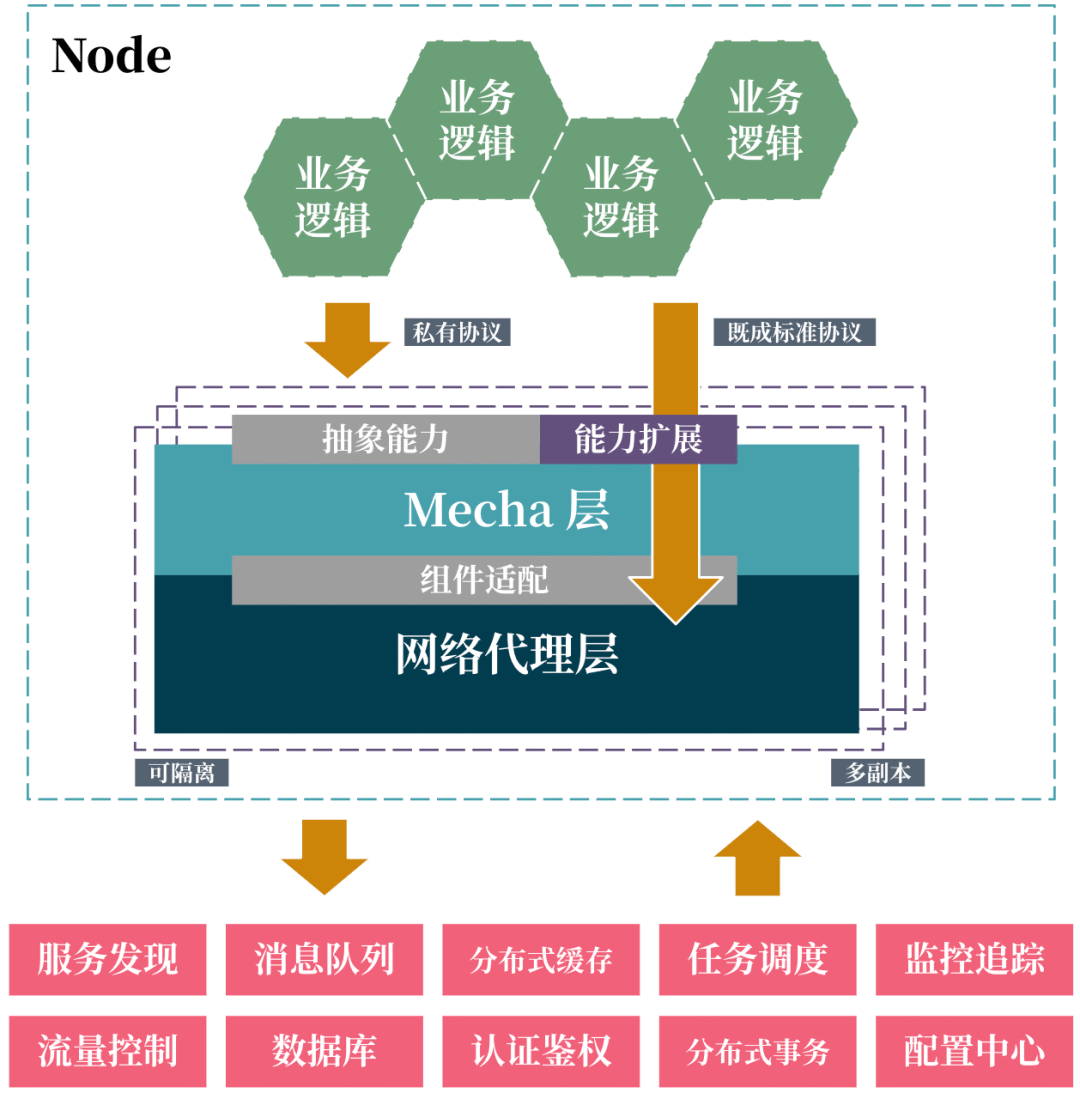
什么是多运行时架构?
服务化演进中的问题 自从数年前微服务的概念被提出,到现在基本成了技术架构的标配。微服务的场景下衍生出了对分布式能力的大量需求:各服务之间需要相互协作和通信,以及共享状态等等,因此就有了各种中间件来为业务服务提供这种分…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...
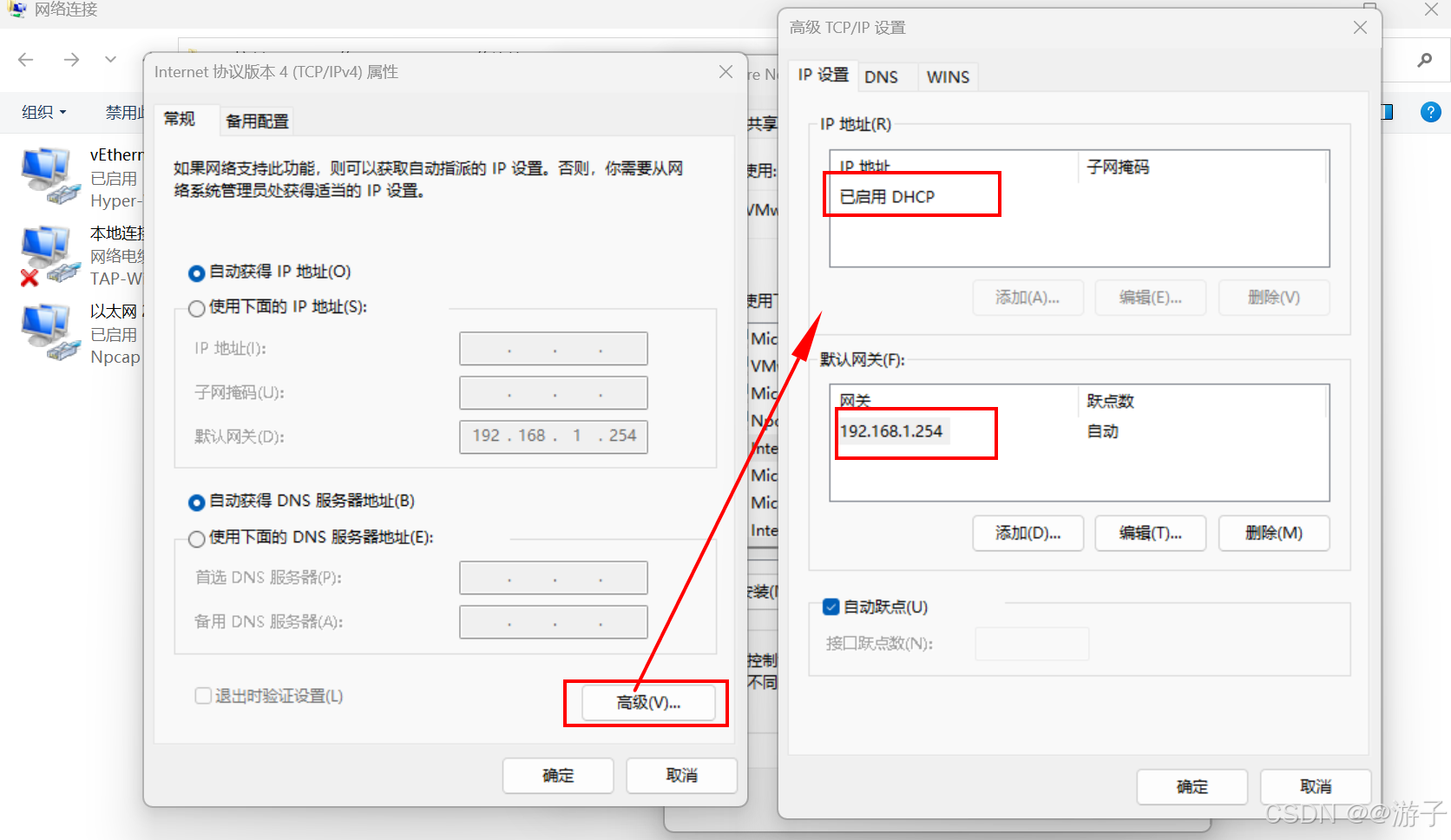
虚拟机网络不通的问题(这里以win10的问题为主,模式NAT)
当我们网关配置好了,DNS也配置好了,最后在虚拟机里还是无法访问百度的网址。 第一种情况: 我们先考虑一下,网关的IP是否和虚拟机编辑器里的IP一样不,如果不一样需要更改一下,因为我们访问百度需要从物理机…...
